重載下基于DE-BP 算法的傳送帶壽命預測模型*

莊曙東 史柏迪 韓 祺

（1.河海大學機械工程學院 常州 213022）（2.梅特勒-托利多國際貿易（常州）有限公司 常州 213022）（3.南京航空航天大學江蘇省精密儀器重點實驗室 南京 213009）

1 引言

在當前互聯(lián)網(wǎng)模式［1］的促進下，快遞業(yè)也快速發(fā)展［2］。帶傳動［3］因其傳動穩(wěn)定、效率高及可維護性強的特性被廣泛運用在物流件裝載之中。但傳送帶因受多種應力的復合作用［4］及實際作業(yè)中受到各類貨物的沖擊極易產(chǎn)生疲勞破壞甚至斷裂，直接影響物流傳送甚至損壞物流件。本課題分析對象為某公司的物流動態(tài)秤，根據(jù)售后故障數(shù)據(jù)因貨物堵包造成皮帶空轉磨損導致皮帶斷裂和長時間變載荷下的疲勞破壞較為常見。

近年來傳送帶的張力［5～6］、預緊力［7］及柔性化傳送［8～9］一直為研究的重點，但卻少有人基于有限元理論建立傳送帶壽命預測模型。傳統(tǒng)基于統(tǒng)計學原理的線性預測模型［10～12］，在線性材料固定接觸中有著良好的預測精度。對于復雜接觸摩擦運動作為多元非線性問題，采用線性模型預測精度難以達到精度。為盡可能挖掘帶速、貨物大小與重量與皮帶壽命之間的關系，使用ANSYS 基于曲面響應法獲取特征樣本。此外因實際有限元方程求解的時間與空間復雜度普通計算機難以進行。故基于樣本集建立預測模型，差分進化算法為基因遺傳算法的改進算法，通過對算子進行自適應化，具有高效并行的特性，基于此算法建立的神經(jīng)網(wǎng)絡可有效避免因初始化不當帶來的梯度消失問題。

2 模型特征

帶傳動中傳送帶應力由三部分組成：拉應力、離心應力以及彎曲應力。當電機功率為P（kW），外包角為α（°），帶輪半徑為d（mm），q 為每米質量（kg/m），中性層與最外層的距離y（mm），則可得其最大應力表達式（1）：

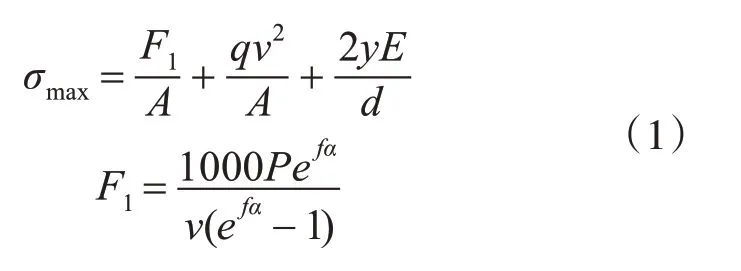
設置帶速為0.667（m/s）結合實際工況下帶的易損特性取式（1）為傳送帶未載重情況下收到的復合應力經(jīng)計算為2.3453×104（N/m2）。本模型參照對象為梅特勒。托利多（METTLER TOLEDO）公司設計生產(chǎn)的LTW155 系列60 動態(tài)秤。在ANSYS 中已經(jīng)完成了其裝配及載重設置圖1。

圖1 TLW155動態(tài)秤模擬載重

設置皮帶等效應力為輸出解。圖2 為當貨物重量為500N，半徑0.15m，且當重物處于傳送帶中央時取得的一組應力解。

圖2 等效應力解

可知傳送帶受到的等效應力對重物重量及尺寸較為敏感。最大應力0.0142（N/mm2）為輸出變量。通過三參數(shù)的S-N曲線式（2）可以將其等效為應力循環(huán)壽命。

式中：N 為待求解的壽命循環(huán)次數(shù)；σf為循環(huán)次數(shù)趨向無窮時的應力；m 為修正系數(shù)由材料及應力方式?jīng)Q定；C為無綱常量；m、C與σf參數(shù)為材料參數(shù)在機械設計手冊中均可查得，經(jīng)計算在上述條件下壽命為6.7×106r。下基于響應曲面法計算在不同貨物重物、幾何尺寸及速度下的循壞壽命。

3 有限元樣本集的建立

3.1 響應曲面法（RSM）試驗設計

RSM 為一種基于最小二乘法的試驗方法。相對于正交試驗法可有效度量輸入值與輸出值之間的變動。在ANSYS 中已經(jīng)集成了RSM 模塊，只需要給定中心點與樣本數(shù)目便可自動進行多次迭代求得答案。圖3為ANSYS中模塊化流程。

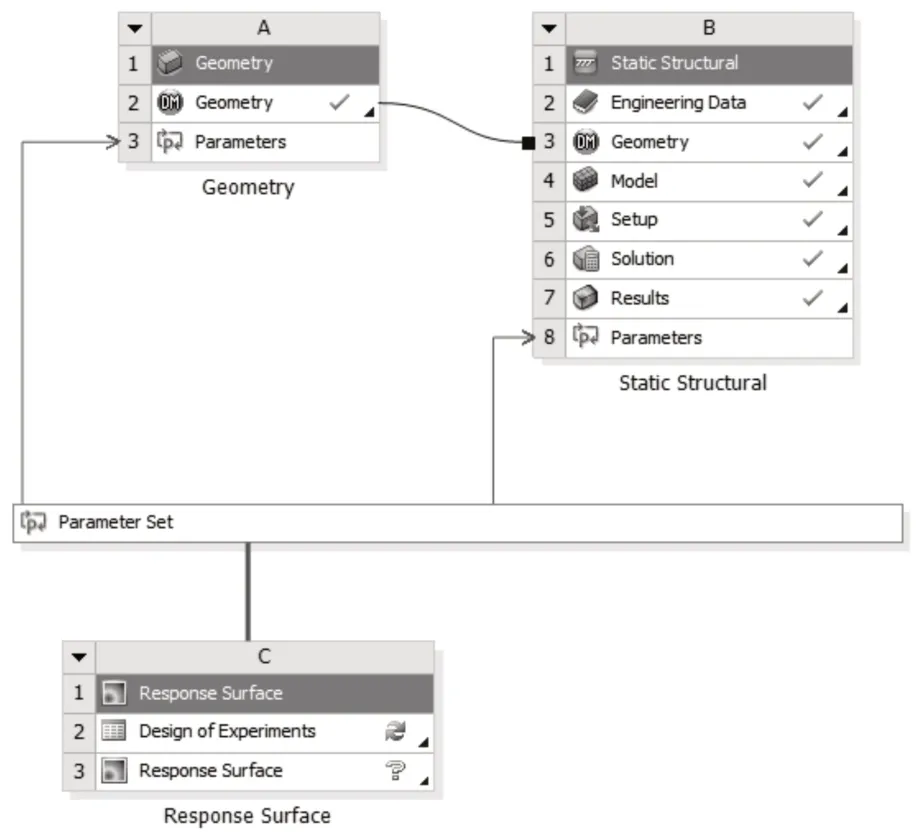
圖3 ANSYS模塊處理流程

圖中包含模型前參數(shù)化處理模塊A、模型有限元求解模塊B及響應曲面模塊C。A 模塊將貨物的外形尺寸半徑r（m）參數(shù)化；模塊B通過對貨物添加正壓力來模擬不同載重狀態(tài)并且對壽命進行求解。響應曲面模塊C 實現(xiàn)樣本集的制取，基于當前輸出對模塊A、B的輸入?yún)?shù)進行修正，并記錄模塊B 解得的壽命。設置中心點為半徑0.15m，載重500N，速度0.667（m/s）試驗次數(shù)為120，可得有限元樣本集。表1為部分樣本。

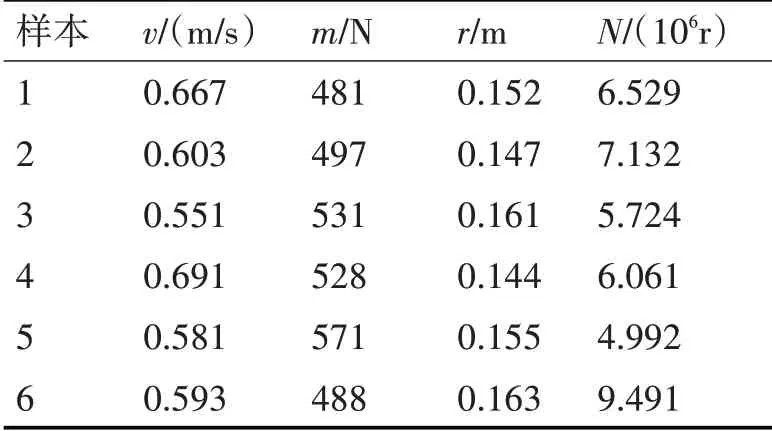
表1 部分樣本數(shù)據(jù)

3.2 樣本集處理

由表1 可知數(shù)據(jù)樣本數(shù)值量偏差較大為防止因數(shù)值量變動對神經(jīng)網(wǎng)絡模型產(chǎn)生梯度異常的現(xiàn)象，基于式（3）對樣本進行歸一化處理。

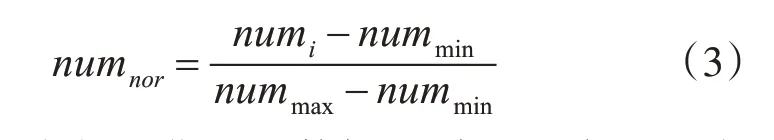
式中：numnor為歸一化后的數(shù)據(jù)，下標min 與max 為該輸入特征的最小與最大值。i 為該樣本序號1 ≤i≤120。對樣本采取5 折合處理，80%樣本作為訓練集學習樣本，余下樣本測試模型泛化性誤差。

4 神經(jīng)網(wǎng)絡預測模型的建立

4.1 神經(jīng)網(wǎng)絡結構

本模型使用BP 神經(jīng)網(wǎng)絡結構，作為一個非線性系統(tǒng)，通過各層網(wǎng)絡中神經(jīng)元對上層信號的加權輸出實現(xiàn)來實現(xiàn)其功能。設置神經(jīng)網(wǎng)絡隱藏層（h）為5，各層神經(jīng)元數(shù)目（m）均為100；輸入為長度為D的向量X；本模型為如下的神經(jīng)網(wǎng)絡結構圖4。

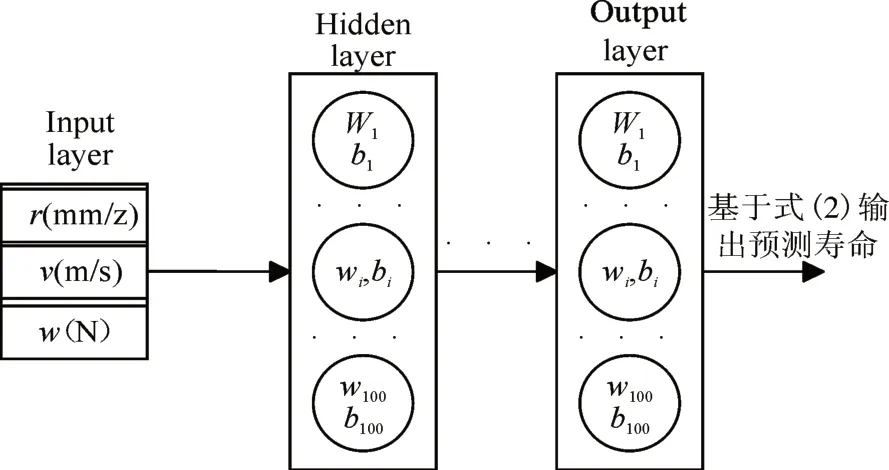
圖4 神經(jīng)網(wǎng)絡結構

設各層網(wǎng)絡輸出值為y，隱含層到輸出層的傳遞函數(shù)為f，輸出層的激活函數(shù)為g在圖4神經(jīng)網(wǎng)絡結構中可得到如下輸出表達式（4）：

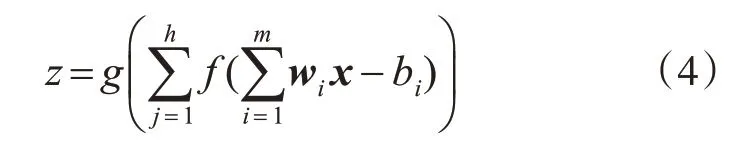
式中：i為神經(jīng)元序列索引（1 ≤i≤m）；j為神經(jīng)元層的索引滿足（1 ≤j≤h）；w為該神經(jīng)元系數(shù)矩陣；為方便后續(xù)進行DE算法種群交叉操作將神經(jīng)網(wǎng)絡權值（w）與閾值（b）改寫為如下矩陣形式（5）。

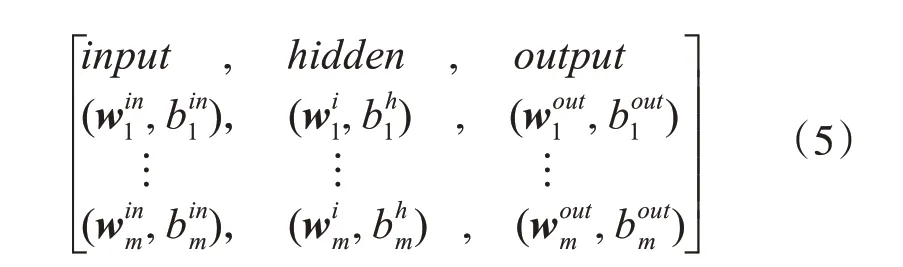
式中：m 為神經(jīng)元數(shù)目取100 與測試集樣本數(shù)目一致；對于input 層w為長度為2 的權值向量，b 為閾值。i 為隱藏層的索引1 ≤i≤5；對于hidden 層與output 層w為長度為100 的權值向量。式（5）即為DE算法中種群個體。

4.2 差分進化算法

差分進化算法［13～14］作為一種群體啟發(fā)式搜索算法無需任何數(shù)學連續(xù)與可導條件。其求解優(yōu)化過程通過模擬生物界優(yōu)勝劣汰，由初始狀態(tài)不斷向最優(yōu)解靠攏。在本神經(jīng)網(wǎng)絡模型中基于最小均方誤差原則可得優(yōu)化目標式（6）。

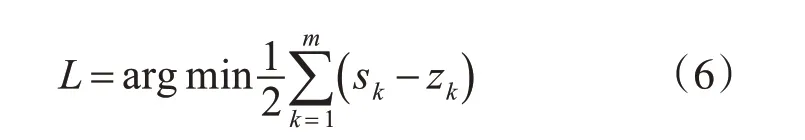
式中，m 為測試集樣本數(shù)目；k為樣本索引；s為樣本實際值；z為式（4）的輸出值。

DE 算法的基本流程包括初始化、變異、交叉、選擇與越界處理。在初始化算法本模型基于Xavier［15］原則進行種群初始化式（7）可避免多層神經(jīng)網(wǎng)絡中梯度消失問題。

式中：m 為隱藏層層數(shù)；i，j 滿足1 ≤i≤m；1 ≤j≤k；w，b為對應隱藏層權值與閾值；h為隱藏層；

為考慮種群的多樣性擴大種群群體搜索能力，采用式（8）進行種群變異。

式中：r1，r2，r3 為隨機選擇的序列號且互不相同；F為變異算子為時常數(shù)因子；V為變異后的種群。

于此同時為添加干擾參數(shù)向量的多樣性通過引入交叉算子CR按式（9）進行交叉操作。

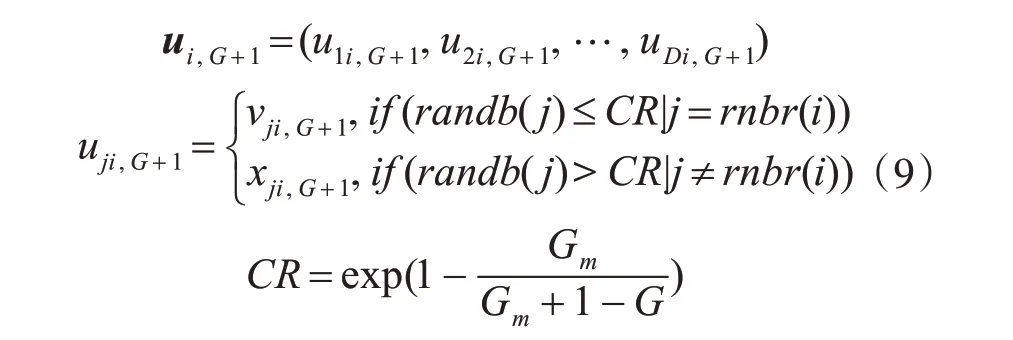
式中：randb（j）表示產(chǎn)生第j 個（0，1）間隨機數(shù)；rnbr（i）表示為一個隨機選擇的序列；i，j 為對數(shù)據(jù)維度的選擇（1 ≤i，j≤D且i≠j）；Gm為最終迭代次數(shù)，G為當前；

對于越界個體基于式（7）重新產(chǎn)生種群。可得差分進化算法初始化種群算法流程圖5。

圖5 神經(jīng)網(wǎng)絡結構

設置迭代次數(shù)Gm 為400，種群數(shù)目N 為100，可得如下種群均方誤差波動曲線圖6。

圖6 均方誤差波動

最終均方誤差可以控制到1000 以下。綜合考慮循環(huán)壽命為106量級有理由相信DE 算法可以有效降低模型初始化均方誤差并避免因初始化不當帶來的梯度異常現(xiàn)象。初始化算法作為一個隨機過程但卻直接決定模型最終可達到的預測精度。

4.3 算法優(yōu)化器

下使用算法優(yōu)化器對神經(jīng)網(wǎng)絡模型進行進一步訓練。與DE算法一致其優(yōu)化目標為最小均方誤差式（6），但在優(yōu)化方法上根據(jù)針對性。其優(yōu)化思想均基于最優(yōu)化原則：沿著誤差的梯度方向可以最快達到目標最優(yōu)解，在圖4 神經(jīng)網(wǎng)絡中可以得到各層神經(jīng)元的誤差梯度式（10）。

式中，η為修正步長；L為式（6）；z，v，w分別為對應隱藏層輸出值，神經(jīng)元激活值與對應神經(jīng)元的向量矩陣；h為層數(shù)索引；j為在h下第j個神經(jīng)元。

當修正步長η已知結合式（10）可以得到權值迭代更新表達式（11）。

式中t 為迭代次數(shù)（1 ≤t≤T）。本模型使用自適應距限制優(yōu)化器（Adam）在式（10）對于步長η有著如下更新原則，設β為慣性系數(shù)；m、v 為一階與二階動量項；η為學習率；τ正則化常數(shù)，則可得如下權值更新式（12）。

Adam 算法通過引入一階二階動量，對誤差進行有效監(jiān)控。隨著迭代的進行自動調整修正量的大小。設置總的迭代次數(shù)為105，正則化系數(shù)τ為10-6選用Adam 優(yōu)化器優(yōu)化經(jīng)DE、GA、粒子群優(yōu)化（PSO）初始化的神經(jīng)網(wǎng)絡可得圖7均方誤差波動。

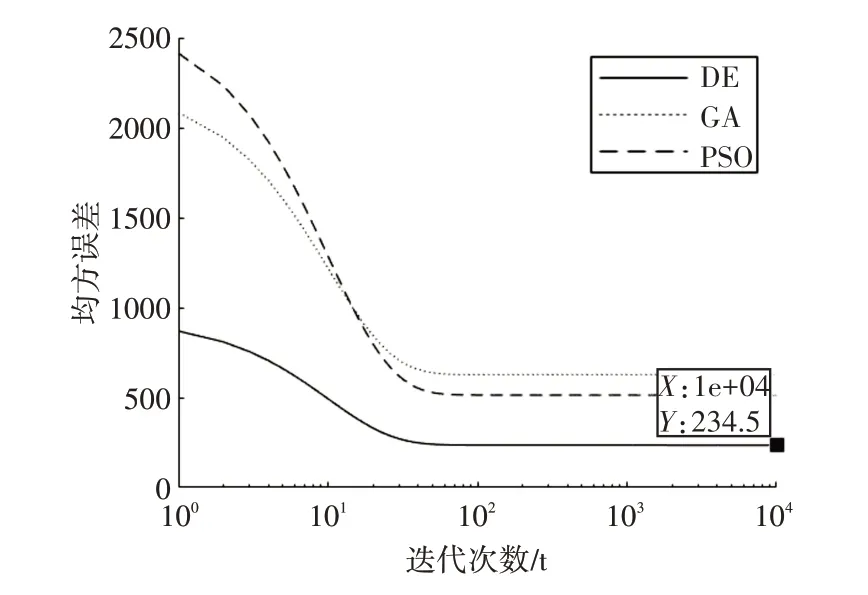
圖7 各算法誤差波動

在圖7 中GA 與PSO 作為群體智能算法其群體數(shù)量與總的迭代次數(shù)條件與DE算法一致。可知經(jīng)DE 算法初始化后，模型訓練后均方誤差最小。下使用測試集對模型進行泛化性測試，取絕對誤差為性能評價指標圖8。

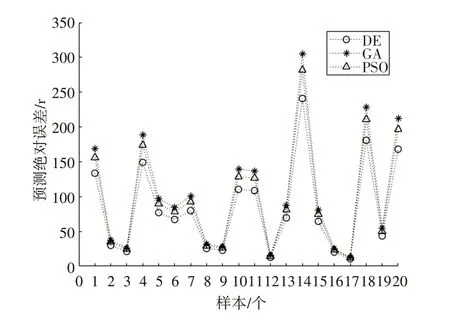
圖8 測試集絕對誤差

圖8 中絕對誤差即為神經(jīng)網(wǎng)絡預測值與樣本差值的絕對值。經(jīng)過計算可得DE、GA 與PSO 初始化后神經(jīng)網(wǎng)絡平均絕對誤差依次為171（r）、212（r）與193（r）。DE 算 法 較GA 與BP 算 法 精 度 提 高23.14%與15.83%。有理由相信此模型可有效進行皮帶壽命預測，從而及時更換保證生產(chǎn)。

5 結語

使用ANSYS 基于曲面響應法可以在特定特征空間內制取數(shù)據(jù)樣本，此外通過使用其Python接口進行二次開發(fā)，建立DE-BP 預測模型可對皮帶壽命進行有效預測，從而保證物流作業(yè)。