一種基于車載電源電壓的隨機數提取方法*

韓 牟 袁曉峰 馬世典 殷志昆

（1.江蘇大學計算機科學與通信工程學院 鎮江 212013）（2.江蘇大學汽車工程研究所 鎮江 212013）

1 引言

隨著汽車智能化、網聯化的快速發展，車內網絡不再是一個傳統的封閉式網絡，外部設備可以通過藍牙、WiFi或者OBD 接口等途徑連接，使得攻擊者對車內電子控制單元（ECU）進行遠程攻擊成為可能［1］。另外，車內ECU 之間的通信是以明文廣播的方式進行的，所有通信內容都可在車載總線上直接讀取，導致攻擊者可輕易冒充ECU 攻擊車內網絡［2］。近年來，層出不窮的智能汽車網絡攻擊事件表明一旦攻擊者繞過了外圍防護，車內網絡中傳輸的數據將輕易被竊取和篡改［3］。綜上所述，車內網絡處于攻擊防護的關鍵環節，但目前其防護手段非常薄弱。因此針對車內網絡通信明文廣播的特點，對其上廣播傳輸的信息進行加密是一種有效的信息安全防護手段。

目前一些研究開展了對車內網絡消息加密的工作，由于車內網絡資源條件受限，導致所設計的加密方法存在安全性不高或者效率不高的問題，難以同時滿足安全性和消息實時性的需求［4］。根據著名的Kerckhoff 假設，密碼系統的安全性不取決于算法的安全性，而取決于密鑰。因此，真正的隨機密鑰對于密碼算法的安全性具有重要意義。從具有不可預測性和不確定性的熵源中獲取隨機數是生成隨機密鑰的一種好方法，這要求隨機數不僅具有良好的統計特性，而且還滿足不可預測性［5］。利用確定性的數學算法可以快速生成偽隨機數，然而這種偽隨機數被證明具有周期性，難以保證密碼系統的安全性［6］。真正的隨機數是一組無偏且不可預測的值，不依賴于生成隨機數的數學算法。它可以是自然界中的各種熵源，如量子噪聲［7］、熱噪聲［8］等，也可以是基于混沌的熵源［9］，通過這些熵源提取出的隨機數稱為真隨機數。Sunar等提出真隨機數的性能受以下三個方面影響：熵源的選取、熵源的采集以及隨機序列的后處理方法，當每個隨機數所攜帶的熵足夠大時，可以認為真隨機數在理論上是非周期性安全的［10］。

因此，本文從車載電源電壓與車輛運行狀態變化之間的耦合關系入手，引入馬爾科夫過程研究車載電源隨機特性的表征方法，進而基于多信息熵源設計一種基于車載電源電壓隨機特性的隨機數提取方法，為隨機密鑰應用于車內網絡奠定基礎。

2 相關知識

2.1 馬爾科夫

馬爾科夫過程是一種特殊的隨機過程，它的原始模型為馬爾科夫鏈，表示為｛X，t=1，2，…，T｝，X為隨機變量，該過程取得的所有狀態空間編號為k（k=1，2，…，K）。在一定條件下具有穩定性，即對于從任意狀態Sn到狀態Sm的狀態轉移概率［11］為

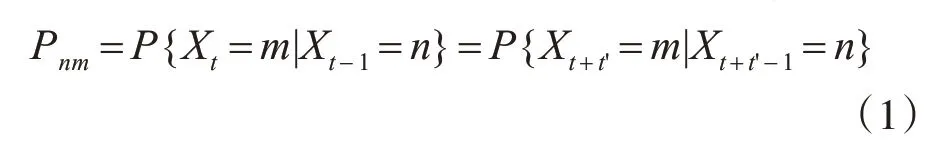
其中，t′=-(t-1)，-(t-2)，…-1，0，1，2，…。

在每個狀態空間下，可以得到狀態轉移概率矩陣：

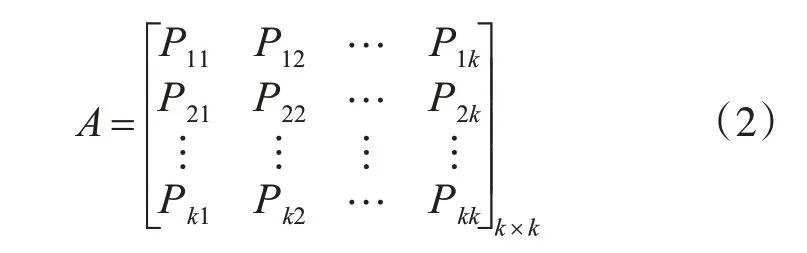
經過極大似然估計的處理，得到狀態轉移概率方程：

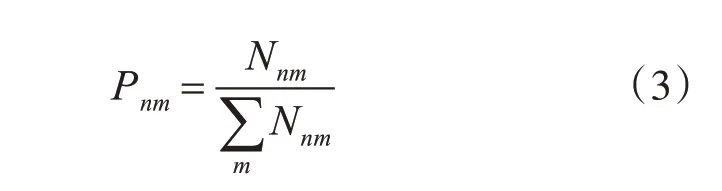
式中：Nnm為時刻t-1 的狀態Sn轉移到時刻t 的狀態Sm的事件數。

2.2 信息熵

1948 年，香農（Claude Elwood Shannon）引入信息（熵），將其定義為離散隨機事件的出現概率［12］。一個系統越是有序，信息熵就越低；反之，一個系統越是混亂，信息熵就越高。所以說，信息熵可以被認為是系統有序化程度的一個度量。

設X 為樣本空間An={a1，a2，…，an}上的離散隨機變量，其概率分布P={pi，1 ≤i≤n}，則X 的熵H1(X)定義為

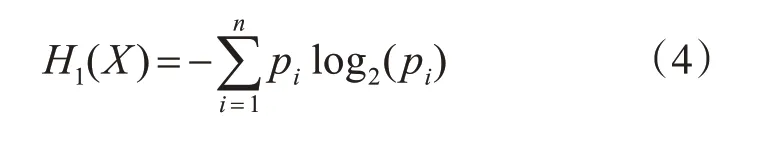
3 車載電源電壓隨機性分析

3.1 ICV駕駛決策影響分析

汽車發電機輸出、其他用電器負載和車載蓄電池共同作用域車載電源系統，直接決定了車載電源電壓的變化。然而汽車是一種典型的以駕駛員（智能決策系統）為中心的系統，通過視、聽覺（傳感單元）感知外部交通環境變化，通過大腦（控制單元）對當前環境進行判斷，并形成駕駛決策，進而控制手和腳（線控執行機構）的運動，完成對車輛的操控。駕駛決策取決于交通因素、車輛因素、天氣因素、道路環境等各種不可預測因素。此外，駕駛行為也受到駕駛風格、心理活動、生理狀態（智能決策系統的感知偏差、傳輸時延、硬件差異）等內在因素的影響。如圖1 所示，各種不同的影響因素之間形成復雜的因果關系模式，最終共同作用于駕駛決策過程，進而導致車輛行駛狀態微觀上的時變特性，這種時變通過發動機轉速的變化耦合到車載電源電壓的變化中，形成了車載電源電壓的隨機變化特性。基于車頭時距模型分析結果［13］，影響車載電源電壓的因素如式（5）所示：

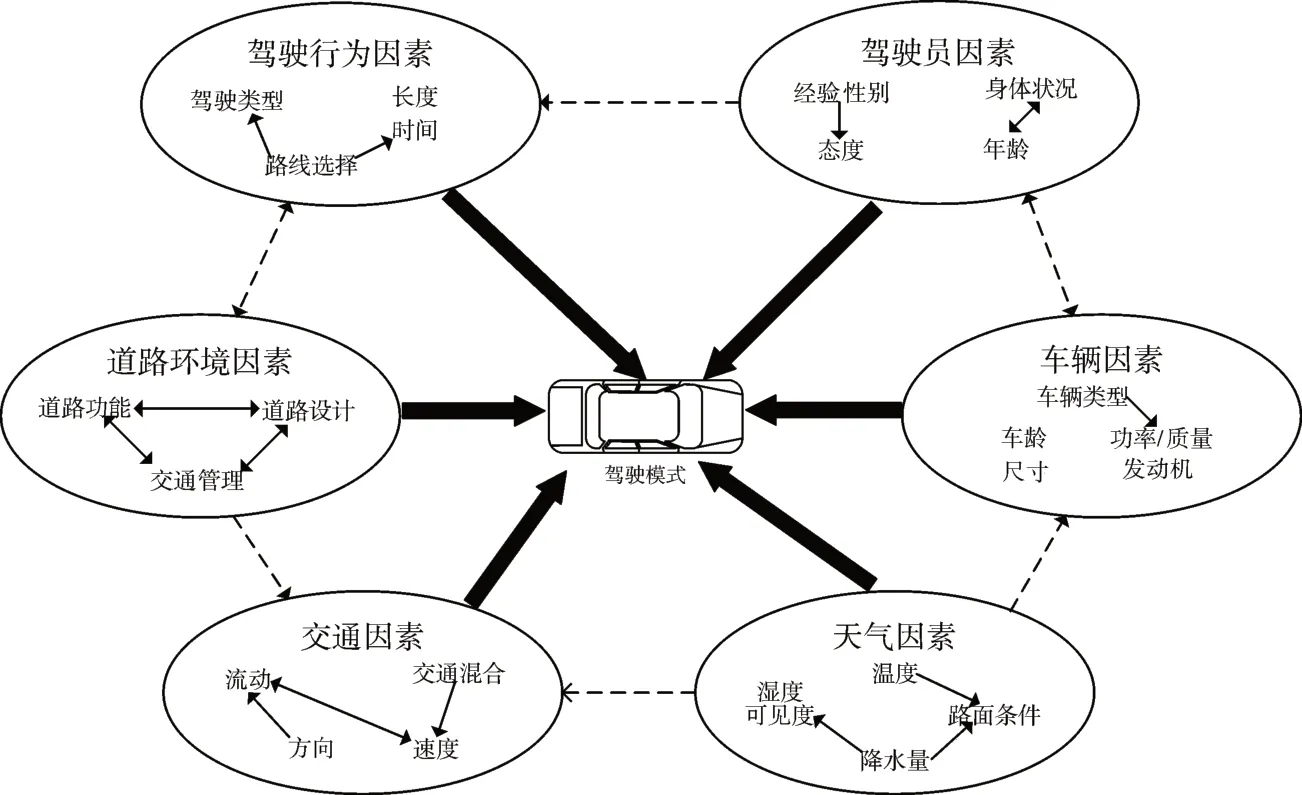
圖1 駕駛模式變化因果模型

式中：V代表車載電源電壓；P代表人為因素；R代表道路環境因素；T代表交通環境因素；W代表交通因素；B代表駕駛行為因素。

3.2 馬爾科夫隨機性分析

為了保持車輛在行駛過程中電壓變化的微小瞬變，反映真實的車載電源電壓特性，將行駛工況下的電壓曲線劃分為幾個反映模型事件多樣性的小片段。本文將行駛工況下的電壓分為三個模型事件，分別為上升期、平穩期和下降期，對電壓數據進行分析，結果如下。

首先，假設采集電源電壓數據總時刻為I，電壓采集時間i（間隔為0.02s）的電壓為vi，對應的電壓變化為Vi，i=1，2，…I。

然后，將電壓變化狀態分為各種族群，總共分為G 族，每一個族都有一個參數θg（g=1，2，…，G）進行估計，每族都含有許多小段時間來反應電壓變化，電壓變化的密度函數表示為

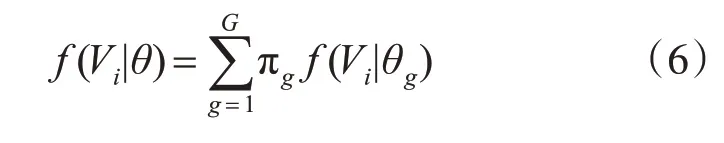
式中：πg為電壓變化Vi在組g中的概率。

最后，利用極大似然估計方法將G族具體劃分，極大似然估計函數如下所示：

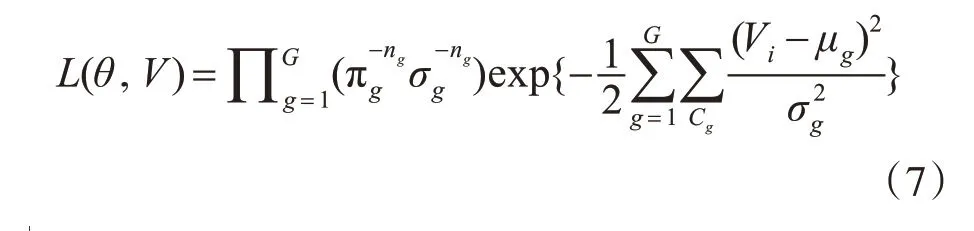
式中：V 為電壓變化矢量；θ為待估參數矢量；Cg為電壓變化屬于組g 的集合；ng為Cg中觀察點的數目；μg為組g 中觀察點的期望值；σg為組g 中觀察點的方差。

經過極大似然估計的處理，將相似類型的電壓變化狀態模型事件聚集在一起。將相同類型的模型事件視為馬爾科夫鏈的一個狀態，不同類型的模型事件則組成了馬爾科夫鏈的狀態空間。將具有相似平均電壓的模型事件構成六個狀態空間：S=｛1，2，3，4，5，6｝，取值區間分別為［12.5，13］、（13，13.5］、（13.5，14］、（14，14.5］、（14.5，15］和大于15，形成馬爾可夫鏈。各狀態的特征參數值見表1。

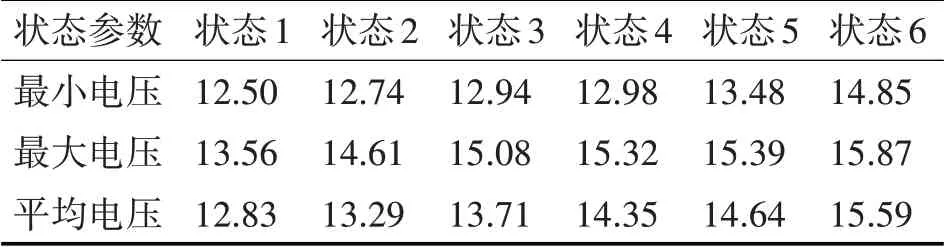
表1 狀態特征參數

本文選取了兩段相鄰加速狀態的電壓，其狀態轉移概率矩陣為

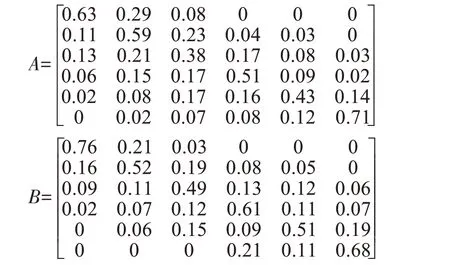
從狀態轉移矩陣B 可以看出，狀態1 轉移到狀態2、狀態3以及本身的概率各不相同，如果當前電壓狀態處于狀態1，則下一狀態取決于這三個概率，而且與B 之前的狀態轉移矩陣A 沒有聯系。因此，車載電源電壓狀態變化是一個具有馬爾科夫特性的隨機過程。

4 隨機數提取方案

4.1 整體框架設計

本文將隨機數提取框架分為四個模塊，分別為：熵源模塊、采集模塊、后處理模塊和存儲模塊，如圖2 所示。其中采用多信息熵融合和小波變換提高熵源質量，經過并行采集和數字后處理得到128bit為一組的隨機序列。

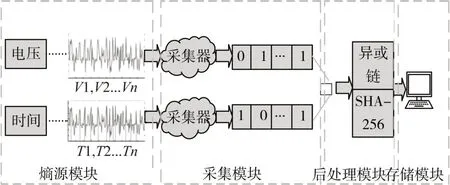
圖2 整體框架

4.2 信息熵增強方案研究

4.2.1 多熵源融合

本文第三節分析了車載電源電壓的特性，發現車載電源電壓變化過程是一個具有馬爾科夫特性的隨機過程。因此，本文采用車載電源電壓作為隨機數發生器的熵源。圖3 展示的是汽車行駛過程中處于不斷加減速和降速工況下的時域和頻域，其中圖3（a）、（b）展示的是不同工況下的時域圖，可以看出車載電壓隨著汽車工況的不斷變化，所形成的波形圖也隨之變化，并且電壓一直處于不斷變化的狀態。然而，在采集過程中發現車載電源電壓波動存在細微的周期性，在圖3（c）、（d）所示的頻域圖中發現每個頻譜中都出現幾處超過10dB 的尖峰，例如圖3（c）中頻率0～15Hz 之間有四處高峰超過10dB，說明在電源電壓信號中存在弱周期性，這將會影響最終熵源的質量。

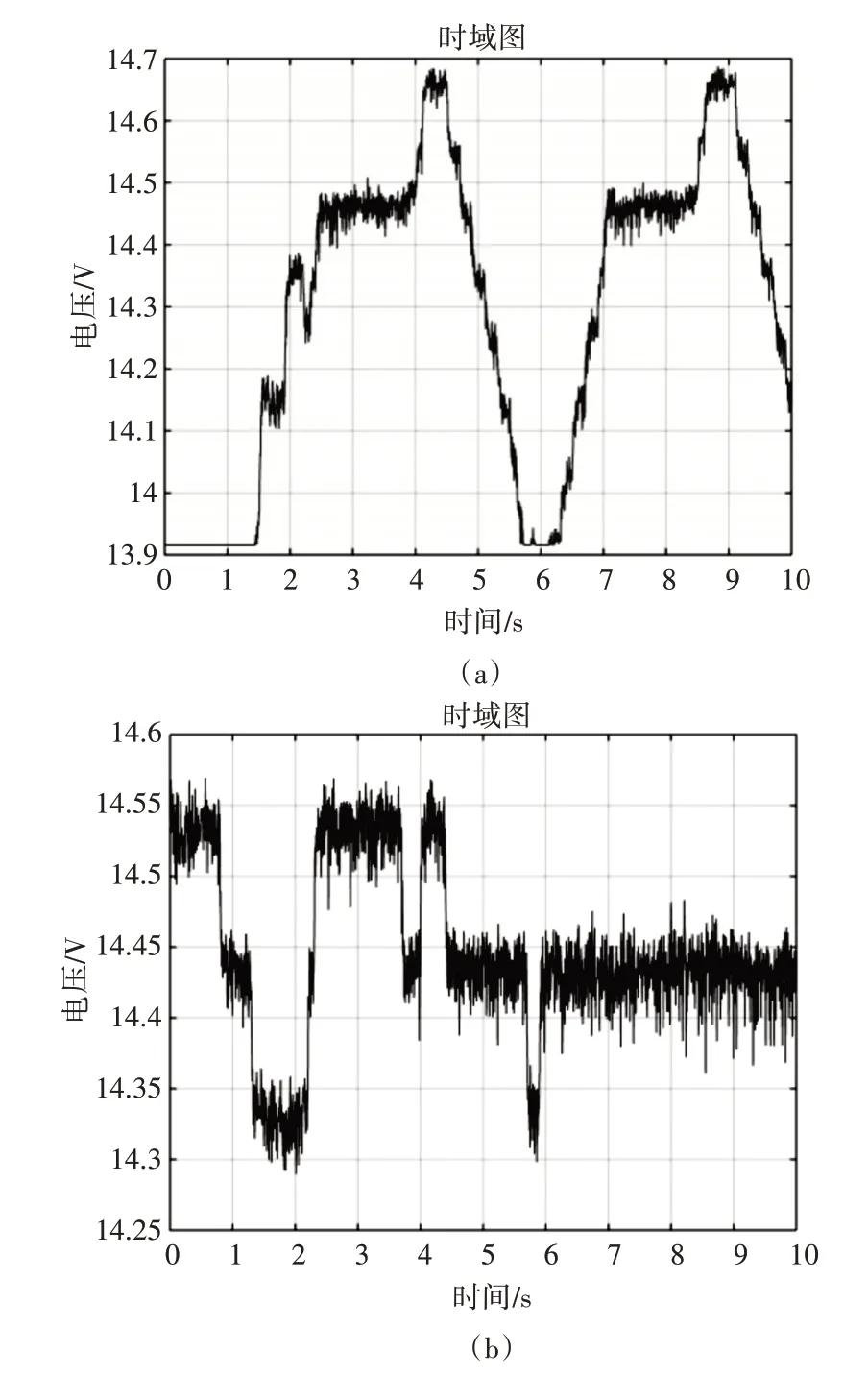
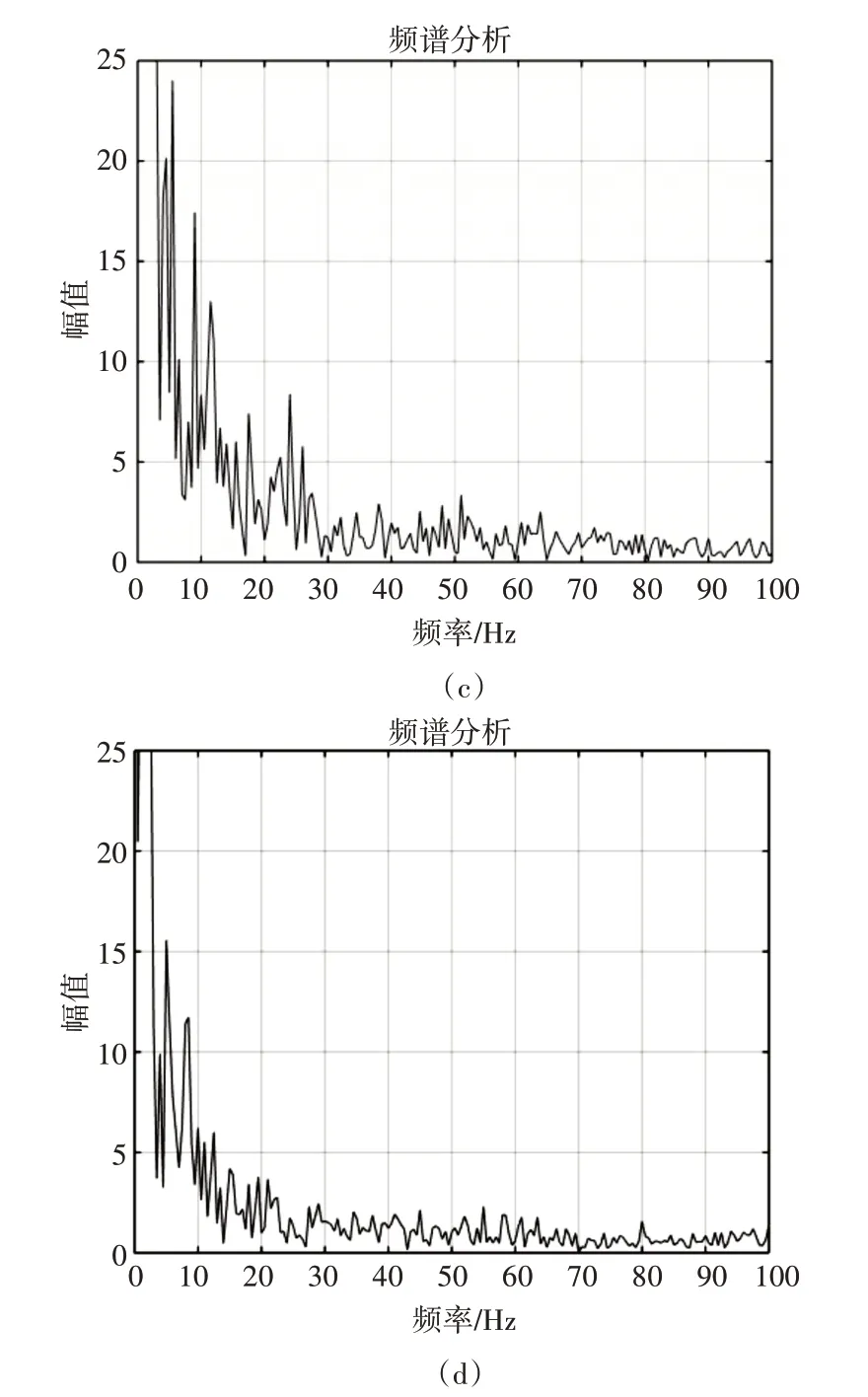
圖3 不斷加減速和降速下時域和頻域

為了消除這種周期性，本文引入了另一種熵源，即高電壓間隔時間。由上述時域圖所知，車載電源電壓一般處于12V～14.5V 之間，超過14.5V 的電壓屬于高電壓，在汽車行駛過程中，電壓會無規律性地達到高電壓范圍內，它們之間的間隔時間存在較大差異。為了增強隨機序列的健壯性和魯棒性，本文采用多信息熵結合在一起，即將高電壓間隔時間和電源電壓轉為二進制序列，然后異或耦合得到最終熵源序列。

4.2.2 基于小波變換信息熵增強

為了改善電壓信號的隨機性，基于小波變換的分解與重構設計了一種濾波方法，主要是過濾電壓信號中周期固定信號，得到隨機性更強的電壓噪聲信號。

在實際采集中，噪聲信號通常為高頻信號，周期信號通常為低頻信號。若要得到非周期性電壓噪聲信號，需要對信號進行小波分析，利用小波的分解與重構進行處理，分解信號如圖4所示。

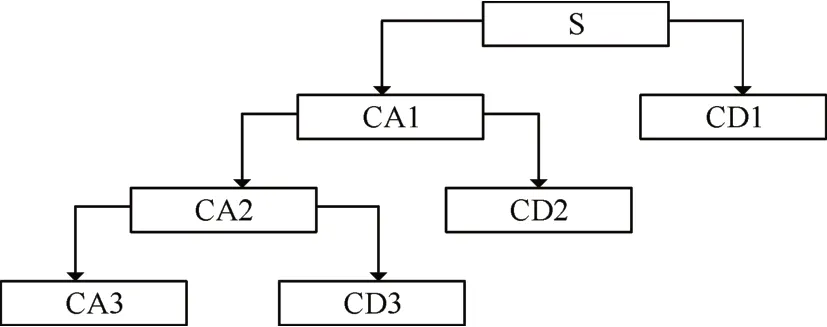
圖4 分解信號示意圖

由于小波分析具有良好的信號適應能力和時頻定位特征，所以能夠將電壓信號進行有效地分解。信號S 經過三層分解后，每次分解結果都得到高頻信號CD1、CD2、CD3，電壓噪聲信號通常在這些高頻信號部分，將分解出來的低頻信號全部重置為零，然后將電壓信號進行重構處理，過濾周期信號，就能得到非周期電壓噪聲信號。

利用Matlab可視化處理軟件處理數據的功能，對其中2000 組電壓信號進行小波分解與重構，如圖5 所示，將原始信號重構為低頻信號和高頻信號，去除了周期信號，我們可以從高頻信號中得到隨機性更強的電壓噪聲信號，從而滿足加密系統對密鑰隨機性的要求。

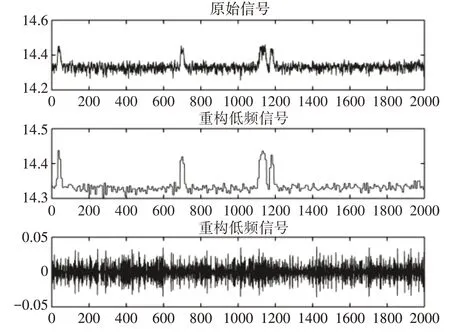
圖5 重構電壓噪聲信號

4.3 采集處理

4.3.1 并行采集

為了提高采集效率，本文采用并行采集異或耦合方法，可以在不降低采集頻率基礎上提高熵值。并行采集結構如圖6 所示，由三種信號、兩個采集器、一個存儲器和一個時鐘組成。本文通過時鐘來記錄兩個高電壓之間的間隔時間，每次電壓超過15V，復位信號就會重置計時器，記錄的時間存儲在存儲器中。目前CAN-FD 總線上傳輸的一幀數據大小最大可達64 字節，因此，本文設置128bit 采樣大小為一個周期，根據實際密鑰需求的大小，通過控制信號來決定采樣周期。

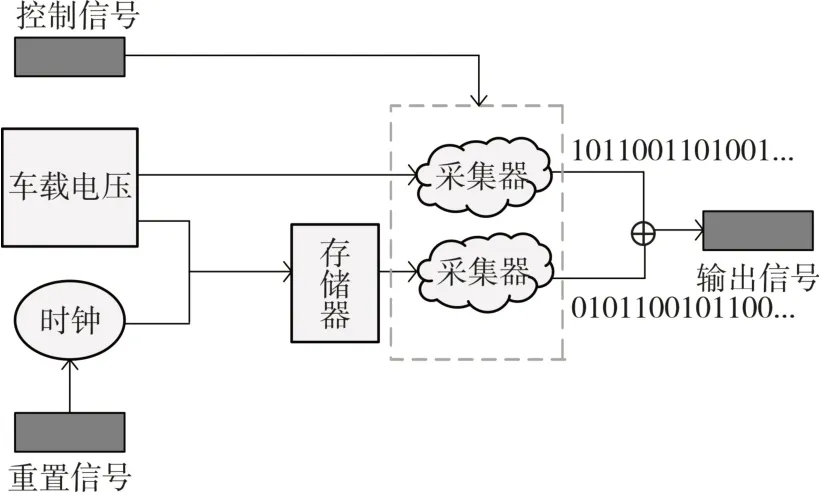
圖6 并行采集結構

4.3.2 數字后處理

在理想的情況下，本文提取的真隨機數0 和1概率應該相等，但實際上，由于電路內部存在其他非高斯型噪聲，并且汽車外部環境對電壓波動的影響，使得其產生的0 和1 概率不可能是絕對相等的。這就必將影響所產生隨機序列的均勻性、偏差以及統計特性，為此必須采取數字后處理方法對隨機序列進行改善［14］。

本文選取級聯異或鏈與哈希函數對隨機序列進行后處理，流程如圖7 所示。級聯異或鏈相當于一個奇偶校驗，可以解決序列均勻分布和偏差問題。在時鐘的節拍下，將采集模塊中數字化電壓-時間信號序列a(i)逐一輸入到6 個D 觸發器中，在存儲移位后，異或鏈將其兩兩異或得到數字序列b(i)，實現了對信號序列壓縮率為6 的壓縮，提高了序列的每比特熵。將得到的序列再經過哈希函數的處理，可以提高數字序列的統計特性。本文采用的是SHA-256 算法，該算法在硬件中的運算速度很快，保證了整個隨機數發生器的效率。SHA-256可以很容易地實現對數據的壓縮，為了盡量不減小數據輸出速度，本文中采用的數據輸入輸出比為1∶1，即輸入256bits，輸出256bits。

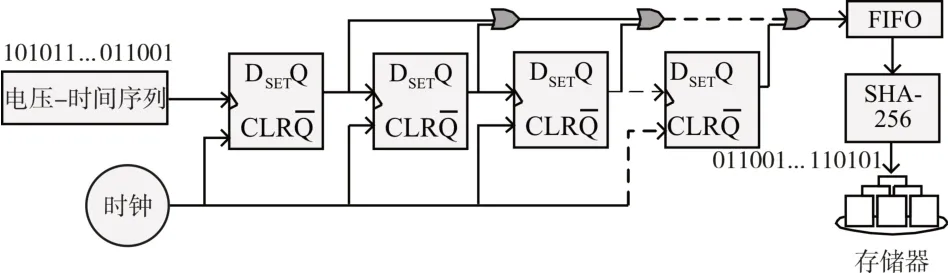
圖7 后處理流程

5 仿真與測試

5.1 仿真提取

本文仿真實驗采用的是帶寬為200MHz，采樣率為2Gs/s 的實時示波器進行采集和觀測存儲，圖8 是怠速和不斷加減速狀態下的實時電壓波形圖，對比兩種狀態下的電壓信號可以明顯看出不同狀態下的電壓呈現不同的波形。同時，示波器采集電壓完成后，還可以從保存的數據中得到高電壓間隔的時間。在采集完熵源之后，將熵源序列分別進行異或鏈和SHA-256 后處理，其中，異或鏈后處理采用的是Synopsys 的Design Compiler 進行邏輯綜合，SHA-256 后處理使用myeclipse 軟件實現。在后處理完成之后，得到最終的隨機數序列。

圖8 怠速和不斷加減速下電壓

5.2 線性復雜度

序列線性復雜度LC（S）的穩定性是衡量其隨機性好壞的一個重要標準［15］。B-M 算法指出只要已知序列的任意連續2LC（S）個元素即可決定整條序列，為了抗擊明文攻擊，隨機序列的線性復雜度應該足夠大。本文利用BM10 函數計算產生序列的線性復雜度，最終得出序列的7 階線性復雜度穩定在49 左右，而常用序列Gold 和Kasami 的7 階線性復雜度為14 和17。因此，本文隨機序列的性能比常用序列的性能要好。

5.3 隨機性檢測

在隨機數提取過程中，本文需要對所得到的序列進行隨機性檢測，看序列是否滿足隨機性。在對隨機數性能測試中，本文使用的是美國國家標準與技術研究院提供的Special Publication800-22 測試包，簡稱NIST 隨機性測試，包括15 種測試手段，這些測試手段可以檢測由硬件產生的真隨機序列的隨機性［16］。經過15 次NIST 隨機性試驗，如表2 所示，所得P-value 值均大于0.001。因此，本文的隨機序列具備良好的隨機性。

表2 隨機性檢測結果

6 結語

為提高車內網絡中密碼系統的安全性，提出了一種基于車載電源電壓的隨機數提取方案。本文對外部交通環境對駕駛決策的影響進行分析，搭建駕駛模式因果模型，并通過馬爾科夫分析電源電壓變化過程。在此基礎上，本方案具有以下特性，以多信息熵融合為初始熵源，采用小波變換過濾周期性信號，并行采集熵源，并利用數字后處理改善序列隨機性。仿真測試結果表明，所提取的隨機數具備良好的隨機性，符合密碼系統中隨機密鑰的要求。