模塊化的應急物資庫存量優(yōu)化模型研究*

胡春玉 李星毅

（江蘇大學計算機科學與通信工程學院 鎮(zhèn)江 212013）

1 引言

自然災害是全球面臨的共同挑戰(zhàn)，而應急物資的儲備問題一直是應對突發(fā)災害工作中的核心內(nèi)容。我國是世界上遭受自然災害影響最嚴重的國家之一，進入21 世紀以來，我國遭受特大地震、低溫雨雪災害、泥石流等不同災害，目前我國中央級的救災物資儲備庫已由10個增加到24個，部分省、市、縣建立了地方救災物資儲備倉庫，初步形成抗災救災物資儲備體系［1］。

近年來，國內(nèi)外學者針對應急物資預儲的問題做了不少研究，如LIU Jie 等［2］考慮了救援物資分配的合理性和有效性，通過MWL-EMA來規(guī)劃應急物資的儲備問題并構建了基于成本的應急物資儲備模型。ZHANG Jianghua 等［3］基于線性規(guī)劃和優(yōu)化網(wǎng)絡，構建了多物資庫和多受災需求點儲備模型。Das 和Hanaoka［4］用連續(xù)的均勻分布函數(shù)來表示救援中訂貨的提前期和需求的不確定性，在此基礎上研究了物資儲備點的訂貨點問題，有效減少了災后因為物資的缺口而造成的損失。朱佳翔、蔡建飛等［5］針對災害信息的不確定性并結合區(qū)間二型梯形模糊集理論和比例分析法，構建了應急物資儲備動態(tài)協(xié)同決策模型，給出了有效的應急物資儲備策略。林琪和趙秋紅等［7］針對應急救援的階段性特點，分析了響應期物資和恢復期物資間的關聯(lián)關系，構建了基于關聯(lián)與替代關系的應急物資儲備量決策模型。丁斌等［10～12］從合作博弈和政企合作的兩個角度出發(fā)，研究了政府與供應商共同合作進行的應急物資儲備策略模型。

不同等級的災害所需要參與救援的儲備庫等級是不同的，而不同等級的儲備庫的保障水平也有所不同，此外，某些物資需要共同輔佐才能更好達到救援效果，鑒于上述研究未考慮到的問題，本文旨在結合物資的模塊性和儲備庫的不同等級能力，構建以物資的需求滿足率最高和儲備系統(tǒng)總成本最小為目標的數(shù)學模型，并采用概率擾動策略設計了NSGA-II改進算法進行模型求解，得出不同模塊的物資在不同等級儲備庫中的最佳儲備量。

2 模型建立

2.1 問題描述和假設

以我國形成的中央、省、市、縣四級儲備體系為研究背景，將儲備庫劃分為四個等級，采用行政隸屬結構來劃分區(qū)域儲備庫層級關系，假設目標區(qū)域內(nèi)有若n 個不同等級的儲備庫R={Ri|i=1，2，…，n}，受災點附近有m 個物資集散中心C={Cj|j=1，2，…，m}。提供物資保障的儲備庫等級參考田衛(wèi)東［13］研究的對于儲備庫參與調(diào)運的層級問題，遵循先地方后國家、就近調(diào)運的原則。災害發(fā)生后，受災點先向當?shù)貎鋷旌推渌诘乇炯墐鋷焐暾埼镔Y救援；需求不能得到滿足時再依據(jù)行政管轄關系向上級儲備庫和與受災點同級的其他儲備庫申報物資；如果依然不能滿足需求，再向更高級別的儲備庫申請援助，依次下去直至國家級層面的儲備庫。

不同于僅僅只考慮單類物資的儲備量決策問題，本文引入軍事物資中的單元化概念［14～15］，在物資儲備的過程中，將具有一定依賴關系的物資進行模塊化處理，即按一定的數(shù)量比例將某幾種物資進行打包，形成物資模塊。災害的種類影響到物資存儲的種類，結合過往災害救援中的先驗知識，設定物資g1，g2，…，gc按照比例a1，a2，…ac組成物資模塊Ak，即物資模塊Ak滿足關系Ak={a1g1，a2g2，…，acgc}，存在單類物資的存儲量與所屬物資模塊的量構成一定的比例關系，并且同一模塊的物資達到受災點的時間間隔在一定的范圍內(nèi)。

災害發(fā)生的初期很難準確獲取物資集散點的需求量，往往是估計性的描述語言，本文采用三角模糊數(shù)來描述一個受災點對物資的需求量，物資集散中心Cj對第s種物資的需求量是一個三角模糊數(shù)，，其中：0 和是三角模糊數(shù)的上下界，是偏好量，即集散中心Ci的需求預置量。集散中心的物資需求偏好量是參考劉宗熹提出的方法來設定的［17］，首先確定儲備區(qū)內(nèi)的總儲量S，由災害范圍R、區(qū)域內(nèi)人口密度ρ、人均需求量決定，S=R×ρ×d，再根據(jù)各儲備節(jié)點的需求指數(shù)We確定各集散點的需求偏好量，需求指數(shù)由一個地區(qū)的經(jīng)濟指數(shù)ei、人口指數(shù)pi和交通指數(shù)ti確定。將每個集散中心的需求量的隸屬度函數(shù)設計為

其中為儲備庫Ri為集散中心Cj提供第s種物資的數(shù)量。

基于以上描述有如下假設：

1）區(qū)域內(nèi)各個儲備庫的位置、數(shù)量和最大容納體積已知，物資儲備量以每人份為單位，在同一個區(qū)域內(nèi)的各儲備點可以相互調(diào)配應急物資，每個儲備庫可以同時向多個集散點提供物資。

2）各個儲備庫到達集散中心的時間已知，忽略道路擁堵、毀壞、運輸工具和裝載空間等限制問題。

3）總成本主要考慮建庫成本、管理成本和運輸成本并且不考慮物資超出保質期而造成的經(jīng)濟損失。

2.2 模型構建

基于上述考慮和假設，構建了如下優(yōu)化目標和約束條件：

目標函數(shù)（3）最小化儲備總成本，第一項是儲備管理成本，第二項是投入建設儲備庫的總成本，第三項是物資運輸成本。其中pis為儲備庫Ri中物資s 的單位儲備成本；bi為儲備庫Ri的固定建設成本；為從儲備庫Ri運輸物資ys到集散中心Cj的單位運輸成本；tij為儲備庫Ri到集散中心Cj的運輸時間；為物資ys在儲備庫Ri中的儲備數(shù)量，是決策變量。

約束條件（4）保證同一模塊的物資到達集散中心的時間差在一定范圍內(nèi)；其中為物資模塊K種物資最慢到達集散中心所用的時間；為物資模塊K種物資最快到達集散中心所用的時間。

約束條件（5）表同一模塊內(nèi)的各種物資在各儲備庫的儲備總量符合一定的比例關系。

約束條件（6）表示庫存物資儲備的體積少于儲備庫的容納體積，其中vs為物資s 的單位體積，wi為儲備庫Ri的最大容納體積。

約束條件（7）表示儲備庫Ri中物資s的存儲量不大于提供給集散中心Cj的數(shù)量。

約束條件（8）表示0-1決策變量，取值為1的時候，表示儲備庫Ri向集散中心Cj提供物資ys，取值為0 時，表示儲備庫Ri不為集散中心Cj提供物資ys。

約束條件（9）保證至少有一個儲備庫為集散中心Cj提供物資保障。

3 模型求解

3.1 改進NSGA-II算法

多目標優(yōu)化問題不同于單目標優(yōu)化問題，當只有一個目標函數(shù)時可以很容易找到最好的解，但是當存在多個目標函數(shù)時并且這些目標存在沖突問題，人們很難找到同時滿足所有目標函數(shù)的最優(yōu)解。帶精英策略的非支配排序遺傳算法（Elitist Non-donminated Sorting Genetic Algorithm，NSGA-II）在求解多目標優(yōu)化問題上表現(xiàn)出較大優(yōu)勢，但是求解過程中隨著迭代次數(shù)的增加，容易收斂到局部最優(yōu)。因此，為了增強后期的種群多樣性和降低陷入局部最優(yōu)的可能性，本文在種群更新過程中加入概率擾動策略來降低陷入局部最優(yōu)的概率，借鑒陳闖［18］設計的一種簡單有效的擾動概率策略以及粒子群算法中粒子每次更新都會利用當代最優(yōu)個體的思想。設計擾動概率公式為

其中：P 是擾動概率；G 是優(yōu)化目標的維度；T 是最大的迭代次數(shù)。借鑒粒子更新公式設計如下擾動公式：

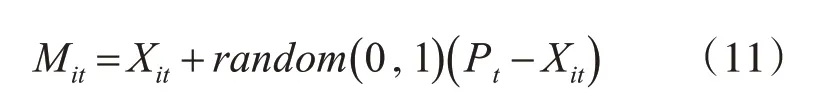
其中：i=1，2，…，N為種群規(guī)模，Mit為擾動后的個體，Xit為第t代種群中第i個個體，Pt為第t代中的最優(yōu)個體。擾動后的個體基于貪婪準則更新，更新公式如下：

其中F(X)是表示個體X的目標函數(shù)值。

3.2 算法實現(xiàn)過程

隨著NSGA-II算法的迭代次數(shù)增加，算法求解會逐漸收斂，通過引入擾動概率來提高收斂于局部最優(yōu)的能力，其算法步驟如下。

第1 步：參數(shù)初始化。隨機生成規(guī)模為N 的種群Pt，當前迭代次數(shù)為0。

第2 步：通過擾動策略產(chǎn)生子代種群Qt。利用式（10）計算擾動概率，通過與初始化隨機參數(shù)的比較判斷是否進行擾動，如需要則根據(jù)式（11）和式（12）分別進行個體擾動和個體更新，然后進行選擇、多點交叉、變異操作產(chǎn)生子代種群Qt。

第3步：非支配排序。將Pt和Qt合并為二倍種群Rt，對臨時種群Rt進行快速非支配排序并計算個體擁擠距離。

第4 步：通過擁擠距離比較算子和精英保留策略選出N個個體，組成下一代種群Pt+1。

第5步：跳至步驟2，并循環(huán)直至達到最大迭代次數(shù)結束。

對應的算法流程圖如圖1所示。

圖1 改進后的NSGA-II流程圖

4 仿真算例

假設某儲備區(qū)有中央級儲備庫R1，省級儲備庫R2，市級儲備庫R3～R6，縣級儲備庫R7～R12，4個集散中心C1、C2、C3和C4。表1 是各儲備庫的固定建設費用和容納量；表2 是各儲備庫到達集散中心的時間。為簡單起見，實驗主要以民眾消耗品為主，滿足災后三天的物資基本保障，其中模塊化物資A1由棉被、帳篷、棉衣褲以2∶1∶4 的比例組成模塊化物資。

表1 擬建儲備庫的基本情況

根據(jù)國家對自然災害的應急響應等級劃分，用改進的NSGA-II 算法對需要啟動Ⅰ級響應的地震場景的算例模型進行優(yōu)化，設置交叉概率為0.9，變異概率為0.2，種群大小100，迭代次數(shù)200，經(jīng)計算得到12 個有效方案，結果如圖2 所示，其中橫坐標為目標函數(shù)成本，縱坐標為滿足率函數(shù)。通過觀察可知成本和物資需求滿足度是相互制約關系，隨著滿足率的提高，所需要的儲備成本和運輸成本也跟著增加，成本投入太少影響受災民眾的需求滿足，投入過多，雖然可以最大化滿足受災民眾的物資需求，但是可能會造成資源浪費，并且失去經(jīng)濟效益和社會效益的平衡，因此在實際決策中需要根據(jù)綜合需求來獲取兩者間的平衡。文中列出了其中一種可行的物資預儲方案，見表3。五種不同的物資是在發(fā)生了需要啟動Ⅰ級響應的地震場景下進行計算得到的各層級不同儲備庫中的分布情況，并且通過計算得知模塊物資接近所設定的比例關系，通過實驗結果可知本模型可以合理有效地用于應急物資儲備體系的優(yōu)化。

表3 各類物資在儲備庫中的分布情況

圖2 迭代200次后的Pareto最優(yōu)

5 結語

本文參考劉宗熹提出的儲備指數(shù)［17］來確定各集散點的物資需求偏好量，通過三角模糊數(shù)描述對災后需求點的物資需求供應的匹配程度，從而構建災后物資供應效果的滿足率目標，有效地避免了因需求不確定對物資儲備決策造成的困難，同時也兼顧了民眾效益。為了更好地達到災后物資救援的效果，基于物資模塊化的概念，將相互輔助搭配使用可以更好發(fā)效果的物資進行模塊化處理，協(xié)調(diào)數(shù)量上的比例關系，并且通過到達時間的限制，從而提高救援的應急響應能力。另外，研究中考慮到不同層級儲備庫具有不同的儲備能力，并且結合各層級儲備庫所需的不同成本來最小化儲備體系的總成本，最后采用添加擾動策略的NSGA-II 算法求解各物資在儲備中的合理儲備量。

目前，本文提出的儲備決策模型并未考慮儲備庫和集散中心的選址問題，因此，在未來的研究中，可以綜合考慮選址和物資儲備兩階段問題模型，另外在實際問題處理中，決策者可以根據(jù)不同儲備區(qū)的實際需求分別賦予兩個目標函數(shù)相應的權重，從而更加合理地儲備物資。