機械應力下電工鋼片磁滯與磁致伸縮回環滯后特性模擬

李夢星 張艷麗 姜 偉 張殿海 謝德馨

（教育部特種電機與高壓電器重點實驗室（沈陽工業大學）沈陽 110870）

0 引言

電工鋼片是構成電磁裝置磁路結構的重要磁性材料，其磁滯與磁致伸縮特性決定了電磁裝置的損耗與振動性能。電工鋼片的損耗、磁滯和磁致伸縮應變對機械應力較為敏感，機械應力會引起磁致伸縮和磁滯回環的變形，導致損耗的增加以及振動幅度的增大。因此機械應力下準確預測電工鋼片磁滯與磁致伸縮回環特性對變壓器、電機的優化設計具有重要意義。

電工鋼片磁滯特性模擬常用的模型有Preisach[1-5]模型，Jiles-Atherton（J-A）[6-9]模型等。磁滯模型發展方向主要為電工鋼片在復雜工況下（如：諧波、直流偏磁、高頻等情況）磁滯特性的模擬。另一方面，電工鋼片磁致伸縮特性模擬[10-11]是以分析實驗和數據為主，并以此建立數學關系式實現的。近年來旋轉磁場下的磁致伸縮特性和機械應力對磁致伸縮的影響成為磁致伸縮特性模擬研究的熱點問題。然而，電工鋼片的磁滯特性與磁致伸縮特性緊密相關，在材料的磁化過程中，90°疇壁的運動會產生磁致伸縮應變，而作為內應力磁致伸縮應變的產生必然會影響磁疇的結構，從而影響磁化過程。當機械應力作用在磁性材料上時，會導致材料內部90°疇壁數量的改變，進而影響材料磁致伸縮應變的產生和磁化過程。因此，建立能同時表征電工鋼片磁滯與磁致伸縮特性，且考慮其機械應力敏感性的數學模型更能真實反映材料的磁化機理。

目前，能夠同時模擬機械應力下電工鋼片磁滯和磁致伸縮回環滯后特性的數學模型還處在探索階段。近年來，從材料磁化過程中動態變化的磁疇能量出發，并將磁疇結構與晶體磁性紋理等考慮在內，基于晶粒內部磁疇總能量極小值的原理，提出了磁疇結構模型(Assembled Domain Structure Model,ADSM)[12]、多尺度模型[13-14]等介觀尺度模型。文獻[12]通過使用ADSM 來對多晶體的磁滯和磁致伸縮特性進行預測，通過引入釘扎能對磁滯和磁致伸縮回環滯后特性進行描述，但該模型僅簡單地描述了磁致伸縮與磁通密度的關系曲線，在軋制和垂直軋制方向上未能有效地模擬出磁致伸縮回環，反映出釘扎能對磁致伸縮回環的滯后效應描述能力尚待完善，并且傳統ADSM 未考慮機械應力的影響。多尺度模型[14]基于無磁滯多尺度模型[13]對單軸應力下磁滯和磁致伸縮特性進行了模擬，該模型通過將不可逆場添加到無磁滯磁場來模擬磁滯行為，并預測單軸應力下的磁滯回環和磁致伸縮回環，模擬結果具有較高的精度，但該模型在引入滯后效應過程中需要額外確定kr、cr、ka和kg四個參數，這些參數與材料有關，進而造成參數辨識過程復雜，不便于工程應用。

為了模擬電工鋼片在機械應力下磁滯與磁致伸縮動態回環滯后特性，本文基于ADSM 磁疇能量極小值思想，提出用磁滯能量代替傳統ADSM 的釘扎能，從磁矩旋轉的角度描述電工鋼片磁滯行為，進而提高ADSM 對于磁致伸縮和磁滯回環的模擬精度。同時引入磁彈性能來描述磁滯-磁致伸縮應變-機械應力的耦合關系，通過晶粒尺度磁特性平均值來獲取機械應力下電工鋼片的磁致伸縮回環和磁滯回環。最后，通過將實驗測得的磁滯回環和磁致伸縮回環與改進ADSM 模擬的回環進行對比，驗證了所提模型的有效性，為電工鋼片物理磁滯模型的進一步工程實用性研究奠定基礎。

1 機械應力下電工鋼片磁滯與磁致伸縮特性

本文借助保變天威集團輸變電技術研究院的一臺激光磁致伸縮測試儀，測量了機械應力下電工鋼片的磁特性。該測試儀通過激光傳感器以10nm/m的分辨率檢測微米級的磁致伸縮應變信號，實驗樣品為寬100mm、長500mm 帶狀電工鋼樣品。激光磁致伸縮測試儀實物如圖1 所示。

圖1 激光磁致伸縮測試儀實物圖 Fig.1 Physical image of laser magnetostrictive tester

圖2 描繪了機械應力作用下通過激光磁致伸縮測試儀沿電工鋼片軋制方向磁化測得的磁致伸縮曲線和損耗曲線，被測樣品為無取向電工鋼片，其中 正值代表拉應力，負值代表壓應力。

圖2 機械應力作用下測得磁致伸縮曲線和損耗曲線 Fig.2 Magnetostrictive curves and loss curves measured under mechanical stress

在圖2a 中，B峰值為1.1T 時，相比于無應力情況下，在機械應力分別為-7MPa、-4MPa、4MPa、7MPa 時，磁致伸縮應變值分別為2.848、2.073、0.898、0.724 和0.384，可以看出：拉應力具有減小磁致伸縮應變的趨勢，而壓應力使磁致伸縮應變增大。同樣地，在圖2b 中，壓應力增加了損耗，拉應力減少了損耗。究其原因，機械應力會改變磁疇的結構，在施加拉應力的情況下，一些磁疇會轉換為與拉應力方向平行的180°磁疇，在施加壓應力時會迫使磁疇轉換為垂直于外部應力平面90°的磁疇。當沿著拉應力方向施加磁場時，180°磁疇僅需通過簡單的疇壁移動就可以完成磁化過程，磁滯損耗主要發生在磁矩旋轉的過程中[15]，因此施加拉應力時會減小損耗，且180°疇壁移動對磁致伸縮沒有貢獻，因此磁致伸縮應變相對較低。相比之下，當沿著壓應力方向施加磁場時，90°磁疇磁化過程中在疇壁移動的基礎上還會產生磁矩旋轉，因此施加壓應力會增大磁滯損耗，且90°疇壁運動是磁致伸縮產生的主要原因，因此在壓應力下的磁致伸縮應變比無應力時更大。

圖3 分別描繪了機械應力下B峰值為1.1T 和1.6T 時磁致伸縮回環和磁滯回環。

圖3 機械應力作用下測得的磁致伸縮回環和磁滯回環 Fig.3 Magnetostrictive loops and hysteresis loops measured under mechanical stress

圖3a 為機械應力分別為-7MPa、0MPa、7MPa時的磁致伸縮回環，相比于無應力情況下的磁致伸縮回環，-7MPa、7MPa 作用下分別使得磁致伸縮回環形狀發生拉伸和壓縮。對于圖3b，0MPa 的磁滯回環面積小于-10MPa。可見，外加應力改變了電工鋼片磁滯與磁致伸縮回環的形狀，影響磁化過程中磁疇的移動與磁矩的轉動，因此，磁性材料磁特性的研究需要采用能夠反映材料物理磁化機理的模型有效地模擬動態磁化過程，才能獲得更加準確的磁特性模擬結果。

2 改進的ADSM

第1 節的測量結果表明，機械應力的作用改變了磁疇的結構，進而引起磁疇能量的變化，本文為了模擬機械應力作用下磁滯與磁致伸縮動態回環特性，提出了改進的ADSM。

2.1 ADSM 的基本思想

磁化過程實質上是磁疇壁的移動以及磁疇磁矩的旋轉，磁化過程是產生磁致伸縮的主要原因，在此過程中會涉及多個能量的動態變化。從熱力學的觀點看，磁致伸縮回環以及磁滯回環上每一個點皆對應磁疇總能量極小值的狀態[16]。電工鋼片為立方晶體結構，由若干晶粒組成，易軸方向為<100>。因此根據ADSM 方案，每一個晶粒的內部皆由六個沿著晶體易軸方向的磁疇構成，結構示意圖如圖4a所示。在ADSM 中，通過將晶粒內六個磁疇的塞曼能、磁晶各向異性能、靜磁能、釘扎能等相加得到的總能量取極小值來獲得每個磁疇的單位磁化矢量的θi和iφ以及每個磁疇出現概率ri。其中引入釘扎能是為了模擬磁性材料的磁滯行為。釘扎類型的磁滯主要是由疇壁運動過程中遇到缺陷或是位錯而產生的[17]。

圖4 多晶結構與磁疇單位磁化矢量示意圖 Fig.4 Schematic diagram of polycrystalline structure and magnetic domain unit magnetization vector

在磁化過程中，每個磁疇的磁矩方向可以用圖4b 的單位磁化矢量表示，在極坐標中第i個磁疇的單位磁化矢量mi可表示為

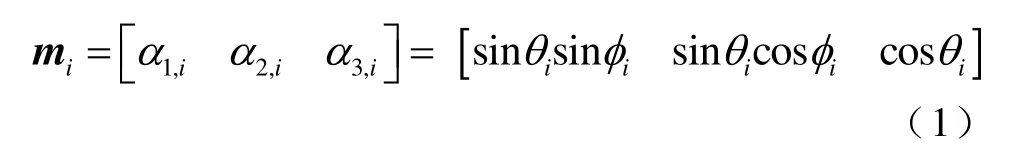
式中，θi為單位磁化矢量與晶體易軸[0 0 1]的夾角；φi為單位磁化矢量在（1 1 0）平面投影與晶體易軸[1 0 0]的夾角。

2.2 機械應力下ADSM 的改進

為了提高ADSM 對磁致伸縮動態滯后特性的表征能力，本文在磁疇尺度用磁滯能量代替釘扎能，從磁矩旋轉的角度描述電工鋼片磁滯行為；同時為了對機械應力下磁致伸縮回環和磁滯回環進行模擬，在磁疇尺度引入磁彈性能來描述磁滯-磁致伸縮應變-機械應力的耦合關系。

磁化過程即是磁疇結構發生改變的過程，而磁疇的結構是磁疇總能量極小值的結果，本文中磁疇總能量包括：①靜磁能Wst；②磁晶各向異性能Wan；③磁彈性能Wσ；④塞曼能Wzeeman；⑤磁滯能量Wh。圖5 所示為磁化過程中磁疇能量作用示意圖。圖5中靜磁能的加入使得整塊磁性材料分成若干自發磁化到飽和狀態的小區域（磁疇），磁晶各向異性能的存在讓磁疇的磁矩均按照晶體易軸排布，磁彈性能改變了磁疇的結構，塞曼能的出現令磁性材料內部磁疇均沿著外磁場方向排布，磁滯能量的引入使得撤去外磁場時，磁疇的磁矩將沿著與外磁場方向接近的易軸方向排布。靜磁能、磁晶各向異性能及塞曼能的計算公式匯總在表1，同傳統ADSM[12]，下面詳細介紹引入的磁滯能量和考慮磁滯-磁致伸縮應變-機械應力耦合關系的磁彈性能。

圖5 磁疇能量作用示意圖 Fig.5 Schematic diagram of domain energy effect

表1 部分磁疇能量計算公式 Tab.1 Partial domain energy calculation formula

機械應力的出現會導致磁疇的結構被改變。在退磁狀態下，外部應力會成為一個新的各向異性源，使磁矩更加偏向于某些易軸對齊，這將會對材料的磁特性產生影響。為了考慮磁滯-磁致伸縮應變-機械應力的耦合關系，磁彈性能被引入磁疇總能量中，該能量的作用類似于各向異性能，第i個磁疇的磁彈性能被描述為

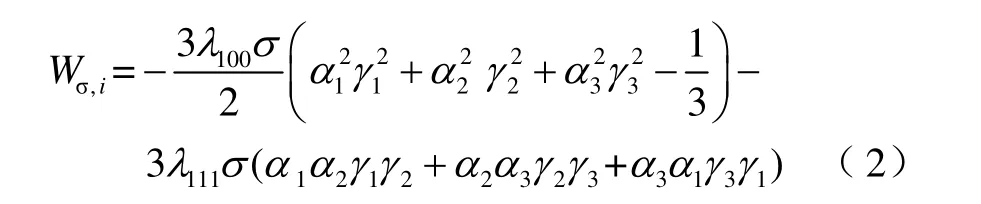
式中，(γ1,γ2,γ3)為應力與晶體的三個易軸的余弦值；λ100和λ111分別為沿著[100]和[111]方向的飽和磁致伸縮常數；σ為外部應力。

磁滯現象發生的過程為[18]：磁滯回環在第一象限從飽和磁場強度減小到零，由于此時材料仍然具有內部磁場（剩磁），因此磁矩的可逆旋轉得以保持。從第二象限開始對材料施加負方向的磁場，此時的磁場是外部磁場與內部磁場的總和，因此材料的凈磁化強度仍然是正的，隨著負方向磁場強度的增加，最終導致磁矩的可逆旋轉不能繼續保持。此時，在各向異性（材料、機械應力）的作用下，磁矩逐漸轉向接近初始磁場方向的易磁化軸，從而引起磁滯現象。從磁滯現象發生的過程可知：磁化過程取決于磁化歷史、磁場強度和應力，磁化曲線上任何具有相同磁化歷史、磁場強度和應力的點都會重疊；機械應力的出現，將會影響晶體織構中的優選易磁化方向。因此只有從磁矩的角度解釋磁滯行為并且考慮機械應力作用下磁化歷史影響的角度來描述磁滯行為，才能準確模擬材料的磁滯特性。引入磁滯能量原因如下[19]：

（1）與釘扎類型的磁滯相區別，磁滯能量是從磁矩旋轉的角度對磁滯現象進行了解釋。

（2）磁滯能量考慮了前一時刻在外磁場與機械應力作用下的磁化分布對當前磁化狀態的影響，通過先前的磁化狀態確定了容易對齊的易磁化軸。本文引入的第i個磁疇的磁滯能量密度函數定義為

式中，χ0為初始磁化率；mx-p、my-p、mz-p分別為上一時刻的單位磁化矢量和在[1 0 0]、[0 1 0]和[0 0 1]上的分量。

晶粒中磁疇皆沿著晶體易軸排布且自發磁化到飽和狀態。在磁疇總能量極小化過程中，6 個磁疇僅代表了在晶粒內部存在的六種不同方向的磁疇，因此本文使用ADSM 參數ri對一個晶粒中第i種磁疇沿著晶體某個方向出現的概率進行表示。采用遺傳算法求解磁疇能量極小值來對每個晶粒中對應于六種磁疇的θ、φ、r進行求解。求解能量極小值過程中涉及的磁疇總能量為一個晶粒內六種磁疇的能量總和，表示為

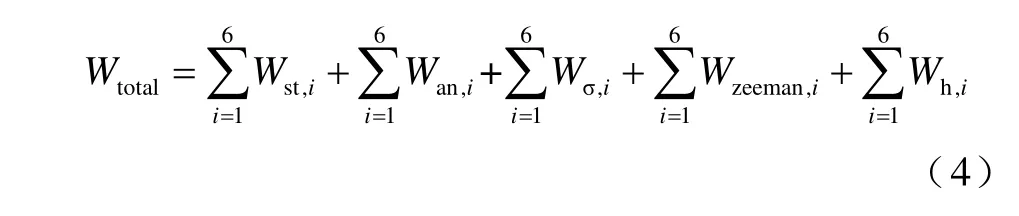
在一個晶粒中總磁化強度和磁致伸縮的表達式分別為

式中，Mgrain為晶粒中總磁化強度；Mi為晶粒中第i個磁疇的磁化強度張量，其與第i個磁疇的單位磁化矢量mi的關系為

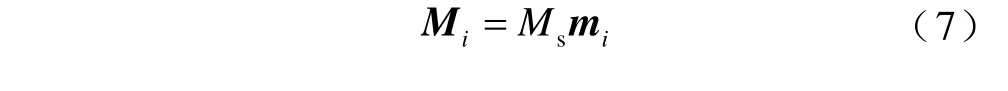
εgrain為晶粒中總磁致伸縮應變；εi為沿著軋制方向的磁致伸縮應變；β1、β2和β3分別為磁化方向與三個易軸的夾角，公式為

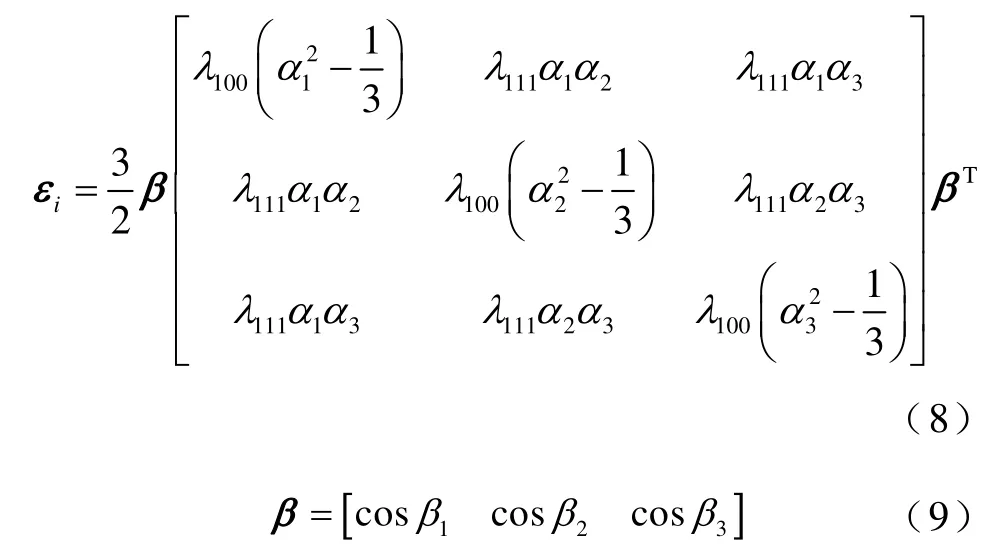
改進的ADSM 最后一步是對多個晶粒的磁特性進行均勻化處理。在多晶材料中每個晶粒都是取向的且與相鄰晶粒不同的單個晶體，因此，可以將多晶體視為許多單個晶體的聚集體[20]。于是多晶體電工鋼片的磁特性可表示為多晶體中各個晶粒的磁特性之和并取平均值

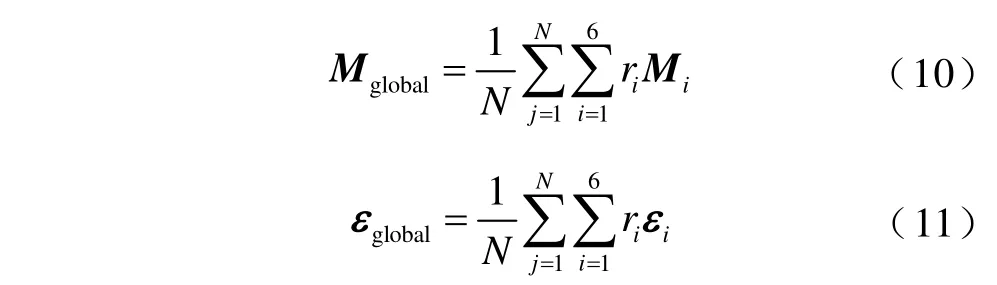
式中，N為可以模擬多晶體磁特性的晶粒數量，為待定參數。磁滯回環和磁致伸縮回環上的每個點由遺傳算法隨機計算N次求和且取平均值進行表示。

3 機械應力下改進ADSM 參數動態辨識與實驗驗證

3.1 多尺度模型動態參數辨識

飽和磁化強度Ms與外部磁場強度H關系通過計算式表示為

式中，Bs為根據實驗測得的磁滯回環得出的飽和磁感應強度。各向異性常數K1為3.8×104J/m，K2項忽略不計[21]。飽和磁致伸縮常數λ100取2.6×10-7[21]，λ111項忽略不計。去磁因子(kx,ky,kz)與樣片的幾何形狀和大小有關，三個去磁因子依次為4.378 2×10-3，3.060 4×10-3，0.925 613 94。

在單晶中χ0隨磁場方向變化而變化，但是在多晶體中，各個晶粒的方向雜亂分布[21]，因此根據計算大致給出，χ0取值為18.63H/m,其計算公式為

式（10）與式（11）中晶粒數量N取值會影響模擬精度，在同時考慮到精度和效率的情況下N取20。

將上述參數值代入改進的ADSM，再利用遺傳算法求取能量極小值后得到描述單位磁化矢量的三個變量θi和φi及ri的值。圖6a 給出了沿著[1 0 0]和[-1 0 0]方向施加磁場時模型模擬出的磁滯回環，圖6b～圖6g 為晶粒內部六個磁疇的單位磁化矢量的φ值在極坐標中的矢量圖，分別對應于圖6a 中A、B、C、D、E、F 點的磁場強度。

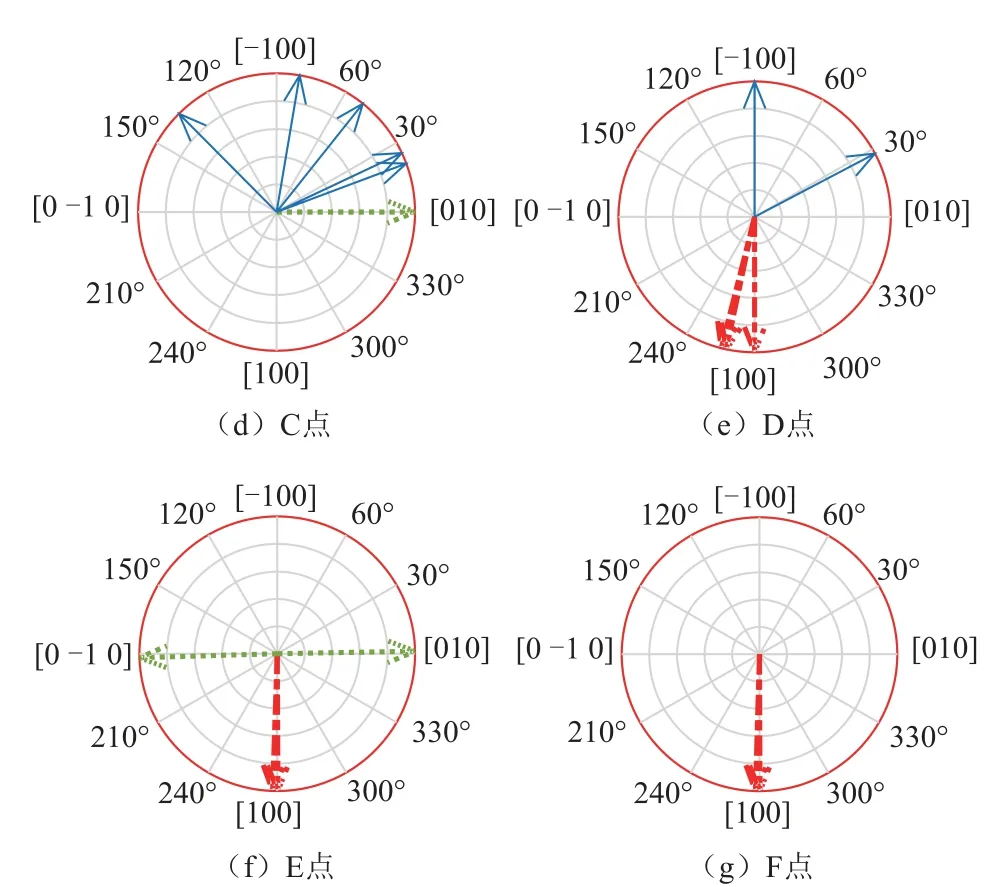
圖6 計算得到晶粒內部6 個磁疇單位磁化矢量φ 值在極坐標中的矢量圖 Fig.6 Calculate the vector diagram of the unit magnetization vector φ value of the 6 magnetic domains inside the crystal grain in polar coordinates

如圖6 所示，圖6b～圖6g 中的箭頭分別表示一個晶粒內部6 個磁疇的單位磁化矢量在（110）平面上的投影（圖中多個箭頭重合處參考表2 中的φi值），點線箭頭表示接近[100]方向磁場的磁疇磁矩，點畫線箭頭表示垂直于磁場方向的磁疇磁矩，實線箭頭表示接近[-100]方向磁場的磁疇磁矩。磁化過程是磁疇磁矩逐漸轉向外磁場方向的過程，當達到飽和時材料中的磁疇磁矩均朝向外磁場方向排布，結合圖6a～圖6g 可以看出，磁場強度由A 點動態變化到F 點，磁矩方向由[-100]方向的飽和狀態逐漸旋轉到[100]方向的飽和狀態。

表2 計算得到的6 個磁疇單位磁化矢量的φi 值 Tab.2 The calculated iφ value of the unit magnetization vector of the 6 magnetic domains（單位：°）

用以繪制6a 中的A、B、C、D、E、F 點對應的6 個磁疇單位磁化矢量的φi值。

3.2 模型驗證

為了驗證模型的有效性，圖 7 給出改進的ADSM 在B峰值為1.6T 時模擬出的磁滯回環與實測回環分別在0MPa 和-10MPa 時的對比情況。從圖7 中可以看出測量值與模擬值吻合度較高，可見改進ADSM 對磁滯回環滯后特性的擬合精度較高。

圖7 改進ADSM 模型磁滯回環精度驗證 Fig.7 Accuracy verification of the improved ADSM model hysteresis loop

另一方面，為了考察改進ADSM 對磁致伸縮回環滯后特性的模擬效果，圖8 給出了在B峰值為0.7T 時用改進ADSM（引入磁滯能量）和傳統ADSM（引入釘扎能）分別計算得到的磁致伸縮回環與測量數據的對比情況。

由圖8 可以看出，相較于傳統ADSM 使用釘扎能模擬出的磁致伸縮滯后特性[9]，改進ADSM 引入磁滯能量后磁致伸縮回環滯后特性的表征能力明顯提高。但是從模擬回環與實測的回環比較來看，二 者吻合并不是很好，這歸因于：本文并未考慮晶粒尺度復雜的耦合關系，即機械應力從多晶體到每個晶粒的轉換與晶粒間的相互碰撞作用。

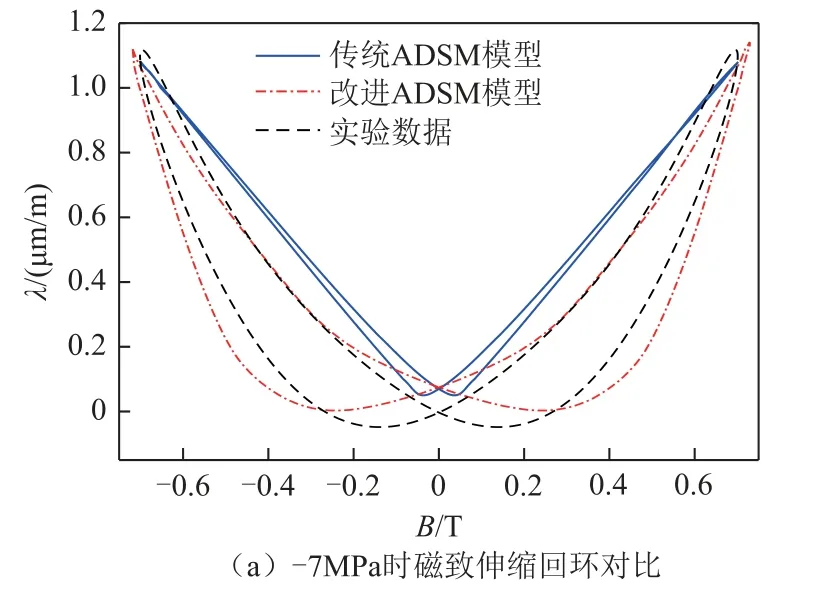
圖8 B 峰值為0.7T 時改進ADSM 模型、傳統ADSM模型計算的磁致伸縮回環與測量數據的對比 Fig.8 Comparison of the magnetostrictive loop calculated by the improved ADSM model and the traditional ADSM model with the measured data when the peak B is 0.7T

圖9 給出了B峰值為1.1T 時改進ADSM 模擬出的磁致伸縮回環與實測回環分別在-7MPa、7MPa、-4MPa 和4MPa 的對比情況。圖10 給出了B峰值為1.4T 時改進的ADSM 模擬出的磁致伸縮回環與實測回環分別在-7MPa、7MPa 的對比情況。

圖9 B 峰值為1.1T 改進ADSM 模型磁致伸縮回環 精度驗證 Fig.9 Verification of magnetostrictive loop accuracy of improved ADSM model with peak B of 1.1T

從圖9 和圖10 中可以看出，改進的ADSM 可以模擬出不同B峰值下的磁致伸縮滯后特性，并且可以較為準確地預測機械應力對磁致伸縮峰值的影響。但是精度方面還需進一步提高，這也是后續待完善的工作。

圖10 B 峰值為1.4T 改進ADSM 模型磁致伸縮回環 精度驗證 Fig.10 Verification of magnetostrictive loop accuracy of improved ADSM model with peak B of 1.4T

4 結論

本文提出改進的ADSM 實現了機械應力作用下電工鋼片磁滯與磁致伸縮回環滯后特性的表征。通過引入磁滯能量，從磁矩旋轉的角度描述和解釋磁滯現象。通過引入磁彈性能來描述磁滯-磁致伸縮應變-機械應力的耦合關系。該模型基于宏觀測量來獲取模型所需要的關鍵參數進而構造模型，通過均勻化的方法來對多晶尺度的機械應力下磁特性進行表示，從而模擬出機械應力下電工鋼片的磁致伸縮回環和磁滯回環。得到的結論如下：

1）通過引入磁滯能量來代替傳統ADSM 中的釘扎能，從磁矩的角度對磁致伸縮回環和磁滯回環進行模擬，從而提高了ADSM 描述磁致伸縮動態回環滯后行為的能力。

2）通過引入磁彈性能來描述磁滯-磁致伸縮應力-機械應力的耦合關系，從而模擬出機械應力下電工鋼片的磁致伸縮回環和磁滯回環。

3）對多個單晶的磁特性進行求解，通過進行均勻化處理來對機械應力下電工鋼片的磁滯和磁致伸縮進行表示。

研究結果表明本文改進的ADSM 模型能夠較為準確地模擬出不同機械應力下的磁滯回環。磁滯能量的引入改善了ADSM 對磁致伸縮滯后效應的描述能力，提高了磁致伸縮回環滯后特性的模擬精度。后續工作會從電工鋼片的晶體結構出發，考慮晶粒間復雜的耦合關系，對提高磁致伸縮回環精度進行研究。