Cooley-Tukey FFT 算法高性能實現與優化研究

郭金鑫，張廣婷，張云泉，陳澤華，賈海鵬

1.太原理工大學 大數據學院，太原 030024

2.中國科學院 計算技術研究所 計算機體系結構國家重點實驗室，北京 100190

快速傅里葉變換（fast Fourier transform，FFT）是處理器基礎軟件生態最關鍵的算法之一，是計算離散傅里葉變換（discrete Fourier transform，DFT）或其逆運算的快速算法，并將算法復雜度由()降為了(lb)。FFT 算法被用于物理、天文學、工程、應用數學、密碼學和計算金融等許多不同的領域。如在國際大科學工程——平方公里陣列射電望遠鏡（square kilometer array，SKA）項目中，FFT 是數據處理的五大算法之一，其計算量占總計算量的40%。由于各應用領域的急速發展及其實時性能的要求持續提高，FFT 在ARM（特別是ARMv8）和X86-64 架構平臺上高性能的實現和優化有著重要的研究意義和應用價值。

雖然FFT算法在ARM和X86-64平臺上已經有比較成熟的實現，如ARMPL（ARM performance library）、Intel MKL（math kernel library）和FFTW（fastest Fourier transform in the West）。但是由于FFT 算 法的復雜性和多樣性，依然有許多工作值得深入研究。例如在庫利-圖基FFT 算法這一目前應用最為廣泛和流行的快速傅里葉算法中，依然存在蝶形網絡復雜、蝶形計算復雜多樣等問題。特別是對于大基的實現，雖然大基通過減少訪存提升性能，但是大基蝶形實現依然存在匯編實現復雜、寄存器不夠用等問題。本文針對這些問題，研究FFT 算法在不同架構CPU 上的高性能實現方法，突破以上問題導致的性能瓶頸，從而實現了一個高性能FFT 算法庫。

在本文的研究中，FFT 算法的實現和優化主要從如下三方面進行：（1）蝶形網絡重構，優化不同基特別是一些大的基，降低蝶形網絡級數，減少訪存提升蝶形網絡性能；（2）利用DFT 矩陣性質，提取蝶形計算公共項，將大基蝶形計算化到最簡；（3）蝶形計算匯編實現，匯編SIMD（single instruction multiple data）優化，寄存器復用策略制定和堆棧內存使用解決寄存器不夠用等。通過以上優化方法的使用，本文在ARMv8和X86-64 計算平臺上突破了大基寄存器不夠用的性能瓶頸，實現和優化了一個高性能快速傅里葉變換算法庫。實驗結果表明本文實現的FFT 算法庫相較FFTW、ARMPL 以及Intel MKL 性能有較大提升，相較算法中小基性能也有較大提升。

本文的主要貢獻如下：

（1）總結和重構蝶形網絡，同時利用DFT 矩陣的對稱性和周期性，大幅降低了大基蝶形計算的復雜度；

（2）總結設計了基14、基20 等大基FFT 蝶形計算方法特別是寄存器使用策略，解決了由于寄存器不夠用導致的性能瓶頸；

（3）提出了一套FFT 算法在ARMv8 及X86-64 架構上的實現策略和優化方案，并構建了一個可跨平臺移植的高性能FFT 算法庫。

1 相關背景

1.1 Cooley-Tukey FFT 算法

離散傅里葉變換是一種用于進行傅里葉分析的基本離散變換，定義如下：

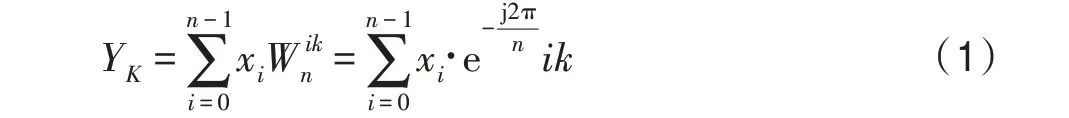
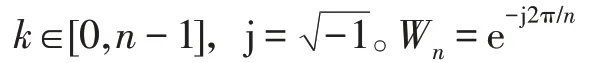
Cooley-Tukey 算法是在許多實際應用中應用最廣泛的快速傅里葉變換（FFT）算法。采取分而治之的方法，通過遞歸將大的DFT 分解為小的DFT。

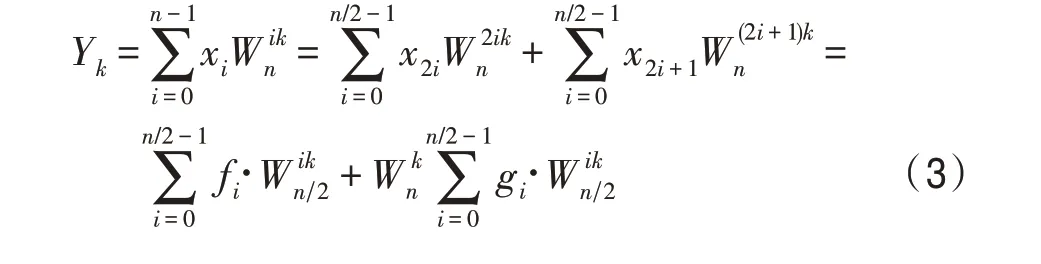
為簡化DFT 運算，利用DFT 矩陣的對稱性周期性將計算時間復雜度由()降到(lb)。

1.2 ARMv8 架構

ARM 是一種負載存儲體系結構，是RISC 處理器的典型。ARMv8 是ARMv7 之后的下一個旗艦架構，向后兼容ARMv7，是首次支持64 位指令集的ARM處理器架構，引入64 位體系結構的同時保持了與現有32 位系統結構的兼容性。

ARMv8 提供了31×64 bit 通用寄存器及32 個128 bit 浮點寄存器V0～V31（如圖1），浮點寄存器在執行指令時一條指令可以操作多個操作數，可以提高指令的執行效率，提高性能。在SIMD 優化中，浮點寄存器起著重要作用。

圖1 ARMv8 架構浮點寄存器圖Fig.1 ARMv8 architecture float register

1.3 X86-64 架構

X84-64 又 稱Intel 64 或AMD64,是X86 指令 集64位版本。Haswell 架構是因特爾公司首個支持AVX2的X86 架構。X86-64 處理器架構提供了17×64 bit通用寄存器（RDI、RSI、RDX、RCX、R8-R15、RAX、RBX、RBP、RSP、RIP），其中RDI、RSI、RDX、RCX、R8、R9作為函數輸入參數；提供了16個256 bit浮點寄存器YMM0～YMM15。Haswell 向后兼容，寄存器低128 bit 可作為128 bit 浮點寄存器XMM0～XMM15。其中XMM0～XMM7 可作為函數輸入參數。XMM 寄存器每條指令可同時處理4 個float 浮點數，YMM 寄存器每條指令可處理8 個float 浮點數。在SIMD 優化，浮點寄存器起著重要作用。

2 相關工作

FFT 算法的研究以主流FFT 庫為主，在特定的硬件架構上實現高性能，包括FFTW、ARMPL、Intel MKL、AOCL（AMD optimizing CPU libraries）、CUFFT（CUDA fast Fourier transform library）等。

2.1 FFTW

FFTW 是MIT 的Frigo 和Johnson 開發的自適應優化FFT 軟件包，用于計算一維或多個維度、任意輸入大小、實數和復數數據以及偶數和奇數數據的離散傅里葉變換DFT。同時支持共享存儲多線程并行和MP（Imessage passing interface）并行，其運算性能遠遠領先目前已有的其他FFT 軟件。FFTW 性能可移植，在大多數架構上性能良好，并且自FFTW3.3.1 開始針對ARM 平臺實現了較高的性能。

2.2 ARMPL

ARMPL 性能庫是ARM 公司針對ARMv8 平臺推出的高性能商業庫。為ARM 處理器上的高性能計算應用程序提供了標準核心數學庫，包含優化的BLAS（basic linear algebra subprograms）、LAPACK（linear algebra package）和FFT，為FFT 計算提供了與FFTW3 相同的接口。

2.3 MKL

MKL 是一個用于科學、工程和金融應用程序的包含快速傅里葉變換的優化數學例程庫。Intel MKL FFTW 是因特爾公司在FFTW 基礎上二次開發的商業FFT 性能庫，是目前X86 平臺上性能最好的FFT 商業庫，但其只用于X86 架構，可移植性差。

3 FFT 算法的實現和優化

3.1 蝶形網絡優化

在Cooley-Tukey FFT 算法中，蝶形網絡決定了數據訪問模式和蝶形計算執行順序。DFT 是逐級求解的，每級重復處理蝶形計算，因此蝶形網絡的組織方式影響整個優化。相同的蝶形網絡，不同的實現和優化可能導致不同的性能。依照蝶形因子在計算中出現的不同位置，實現該算法有兩種方式：時域抽取（decimation-in-time，DIT）和頻域抽取（decimation-infrequency，DIF）。時域抽取時，蝶形因子在計算輸入端，輸入向量需位反轉，輸出自然順序；頻域抽取則相反，蝶形因子在計算輸出端，輸入向量自然順序，輸出需位反轉。

傳統蝶形網絡存在位反轉操作，如圖2 所示，增加了額外的內存成本，還增加了混合基建立的困難度，對SIMD 不友好。本文采用了如圖3所示的Stockham蝶形網絡結構。

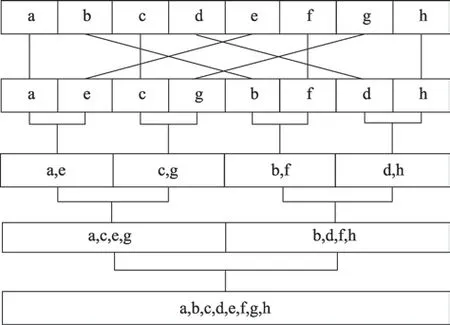
圖2 時域抽取Fig.2 DIT network

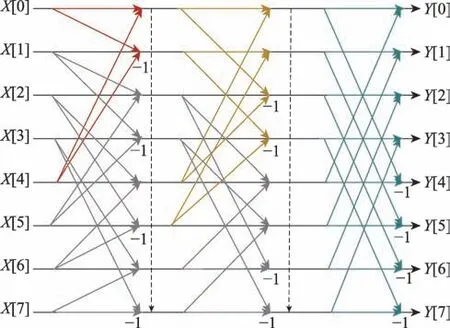
圖3 Stockham 蝶形網絡Fig.3 Stockham butterfly network

Stockham 蝶形網絡結構相比傳統蝶形網絡：（1）去除了位反轉排列，DIT 時域抽取需要將輸入序列重新排序為位反轉順序，位反轉排列引入了額外的不連續的內存訪問，不連續的內存訪問會導致統一輸入輸出的內存訪問困難。Stockham 蝶形網絡各級計算的輸入輸出都是自然順序，消除了位反轉排列，統一了蝶形網絡的訪存行為。（2）SIMD 友好，SIMD 為一條指令作用在多個數據操作上，為了有效使用SIMD，從內存中加載和存儲到內存中的數據應是連續的，Stockham 蝶形網絡結構中，蝶形網絡的輸入輸出是連續定位的，在同一級內SIMD 并行化友好。（3）混合基友好，由于每級的輸入輸出都是自然順序，不同RADIX 算法采取統一的方式，可以完美融合在一起。

為了得到更好的性能，將第一級蝶形網絡單獨優化。第一級蝶形網絡的旋轉因子為1，沒有必要從內存中讀取和計算，降低了不必要的內存訪問和計算成本。第一級輸出結果的寫入并不連續，在匯編優化時需要再進行數據重組和轉置。

蝶形網絡帶寬依賴較高，由于每一級內存訪存寫入，蝶形網絡級數過多會增加數據訪問量。使用大基參與FFT 計算可降低蝶形網絡的級數，減少數據訪問量。雖然大基參與蝶形網絡計算，寄存器不夠用，一定程度上降低了蝶形網絡性能，但使用大基參與計算帶來的性能增益優于性能損耗。

3.2 蝶形計算優化

在FFT 計算過程中，蝶形計算反復調用，蝶形計算的性能將直接影響FFT 算法的最終性能。因此，本節將介紹如何將FFT 蝶形計算的復雜度降到最低。根據離散傅里葉變換式（1），基(Radix-)的蝶形，本質上就是長度為的DFT 計算，而DFT 計算的實質即DFT 矩陣與輸入矩陣向量乘法。

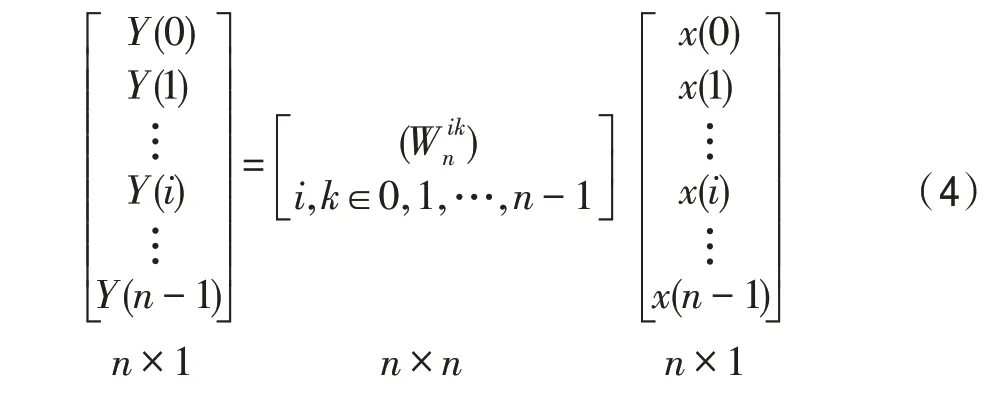
由于當基較小時已經有了成熟的計算方案，本文將研究大基的高性能實現方法，如基14 和基20。

下面將詳細地分析Radix-14 的蝶形計算方法。Radix-14 蝶形計算本質上是數據規模為14 的DFT計算。

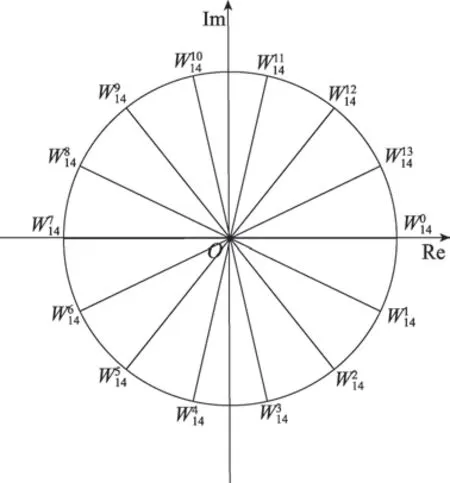
圖4 Radix-14 旋轉因子復平面分布圖Fig.4 Radix-14 twiddles complex plane distribution

根據Radix-14 在如圖4 所示復平面上的分布旋轉因子關于軸和軸對稱：實部相同虛部互為相反數；虛部相同實部互為相反數。

式（1）旋轉因子具有如下性質：

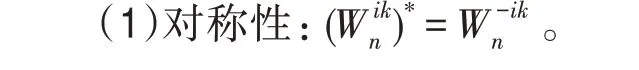
通過提取和預計算公因子，可以減少浮點計算和代碼冗余，將蝶形計算的時間復雜度降到最低。

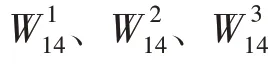
3.3 SIMD 優化

ARMv8 提供了32 個128 位的浮點寄存器，每個浮點寄存器可以存儲4 個32 位的單精度float 浮點數或2 個64 位雙精度double浮點數，一條指令最多可以同時并行處理4 個數據。在ARMv8 體系結構中，使用2個128位寄存器分別容納4個復數的實部和虛部。

X86-64 架構提供了16 個256 位的浮點寄存器，X86 架構SSE 指令可以用128 位通路XMM 浮點寄存器處理4 個32 位的運算或處理2 個64 位的運算。X86-64 AVX 指令是SSE 的兩倍，可操作16 個YMM 256 位浮點寄存器。并行操作1～8 個單精度float 浮點數，1～4 個雙精度double 浮點數。在Haswell X86-64 體系結構中，使用一個256 位寄存器交錯容納4 個復數的實部和虛部。

FFT 計算時，每個蝶形計算相互獨立。如圖5 所示SIMD 優化同時處理4 個蝶形計算，提高了程序的并行效率。

圖5 SIMD 優化Fig.5 SIMD optimization

高級語言程序，一般由編譯器負責寄存器使用。為提高FFT 算法性能，本文蝶形計算過程采用匯編語言。通過寄存器使用優化，可提高算法的性能。寄存器使用的主要思想是寄存器分組。浮點寄存器的使用分為輸入寄存器in，旋轉因子寄存器twiddles，中間結果寄存器scratch 及輸出結果寄存器out。ARM 架構復數實部虛部需要×2 個in 寄存器，(-1)×2 個tw 寄存器，×2 個輸出out寄存器；X86-64架構需要個in寄存器，-1 個tw寄存器，個out寄存器。隨著基數的增長，4 組寄存器需要更多的向量寄存器，寄存器資源無法獨立完成蝶形計算。

寄存器優化分為兩部分：一部分為寄存器復用；一部分為極大基臨時存入堆棧或內存。寄存器復用策略：復用旋轉因子臨時寄存器tmptw，輸入和旋轉因子數據相互獨立，寄存器使用緊張時分批加載旋轉因子，完成復數乘法后，繼續復用tmptw，在全部完成旋轉因子輸入乘法后，釋放tmptw；復用臨時輸入寄存器tmpin，在加載部分輸入后，計算中間變量，釋放tmpin 以復用；復用臨時寄存器tmp，在乘法等運算時需要臨時寄存器，這時的臨時寄存器需及時復用處理運算；復用tmpout 輸出寄存器，在獲得輸出后，立即存儲在內存，釋放tmpout以復用。

（1）在大基的情況下如Radix-14，浮點寄存器的合理充分利用，直接影響FFT計算程序性能。ARM架構寄存器合理復用的同時存在不夠用的情況。需將公共因子臨時存入堆棧，計算輸出結果時載入寄存器。

ARM 架構中，Radix-14 的Kernel 計算：中間結果scratch 實部虛部分別需要26 個浮點寄存器。輸入數據和旋轉因子成對載入，輸入數據乘以旋轉因子后載入下一對數據時計算中間結果，復用旋轉因子和輸入數據寄存器；計算中間結果后，+類中間結果寄存器可復用計算；計算過程中將通過寄存器分配無法分配溢出的中間數據+，-存入堆棧，計算輸出out 時取出；蝶形計算結果及時輸出釋放復用輸出寄存器。寄存器復用中間處理足夠多的指令可消除相鄰指令寄存器依賴，達到蝶形計算寄存器最大化合理利用。

X86-64 架構中，Radix-14 的Kernel 計算:中間結果scratch 需要26 個YMM，旋轉因子寄存器在乘以輸入后重復復用；輸入寄存器計算中間結果后釋放復用為中間結果寄存器。通過寄存器合理復用即可實現Radix-14 蝶形計算。

（2）在極大基的情況下，如Radix-20，X86-64 架構提供的16 個YMM 寄存器，ARM 架構提供的32 個V0～V31 浮點寄存器遠不夠用。通過復用寄存器，寄存器仍不夠用，此時需要使用堆棧或內存指令暫時保存相關數據，蝶形計算需要時取出載入寄存器。

ARM 架構中，Radix-20 的Kernel 計算：中間結果scratch 實部虛部分別需要50 個浮點寄存器。數據載入時分奇偶序列分開載入；輸入寄存器和旋轉因子乘運算后，復用旋轉因子寄存器；輸入數據載入后及時計算，復用輸入數據占用的寄存器；計算過程中寄存器占滿32 個，通過寄存器分配策略將計算輸出頻繁用到的S 類中間數據存入堆棧釋放所需寄存器，需要使用時再取出；蝶形計算結果及時輸出釋放復用寄存器。

X86-64 架構中，Radix-20 的Kernel 計算:中間結果scratch 需要50 個YMM。數據成對載入，及時計算中間變量，復用輸入寄存器；寄存器分配策略將無法占用寄存器的相關數據存入內存，計算輸出結果時載入寄存器；蝶形網絡計算第一級輸出結果存儲轉置時，還需將部分輸出結果存入內存，數據操作時載入寄存器。

指令選擇時，選擇延遲低吞吐量高的指令。X86-64 選擇vfnmadd231ps 和vfmadd231ps 乘加指令，ARMv8 選擇fmla 和fmls 乘加乘減指令。AVX2 還提供了vaddsubps 指令來完成交錯模式下的復數乘法。如圖6 列出了幾種運算的指令對比。在ARM NEON中支持ld2、st2 高效的加載存取指令，因此ARMv8 使用ld2、faddp、st2 等指令進行復數算數運算。

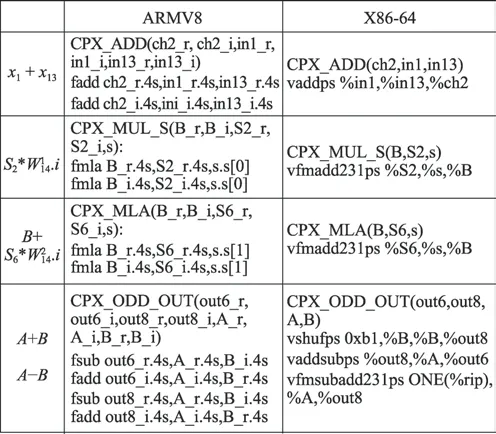
圖6 計算指令對比Fig.6 Instruction comparison

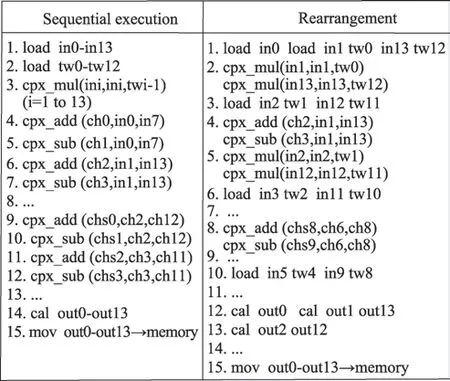
圖7 順序執行與指令重排對比Fig.7 Sequential execution and instruction rearrangement

相鄰指令間沒有依賴關系時可指令重排，避免了流水線stall。指令重排和順序指令相比并不影響計算結果，但性能會有一定提升。如圖7 是基14 指令重排對比圖，順序執行過長時間占用寄存器，寄存器還不夠使用，寄存器得不到有效利用，指令重排將載入數據的順序調整后及時計算中間結果。在中間結果計算后，釋放輸入寄存器的占用，供輸出結果復用。在Radix-14、20 這類大基計算時，指令重排配合寄存器的合理分配優化，一定程度上提高了算法的計算性能。

4 性能評估

4.1 測試環境

本文采用華為鯤鵬920 CPU和IntelXeonCPU E5-2640 V4 作為性能測試平臺。華為鯤鵬920 CPU采用ARMv8 架構，IntelXeonCPU E5-2640 V4 采用X86 架構。本文實驗條件如表1 所示。

由于FFTW、ARMPL、Intel MKL 是應用最廣泛、最成熟的FFT 算法庫，將OpenFFT 的性能與這些庫進行了比較。采用FFTW3.3.8 和ARM 公司的商業庫ARMPL20.0.0 在ARMv8 平臺上進行性能對比；采用FFTW3.3.8 和Intel MKL 在X86-64 平臺進行對比。本文實現的高性能FFT 算法庫為OpenFFT。

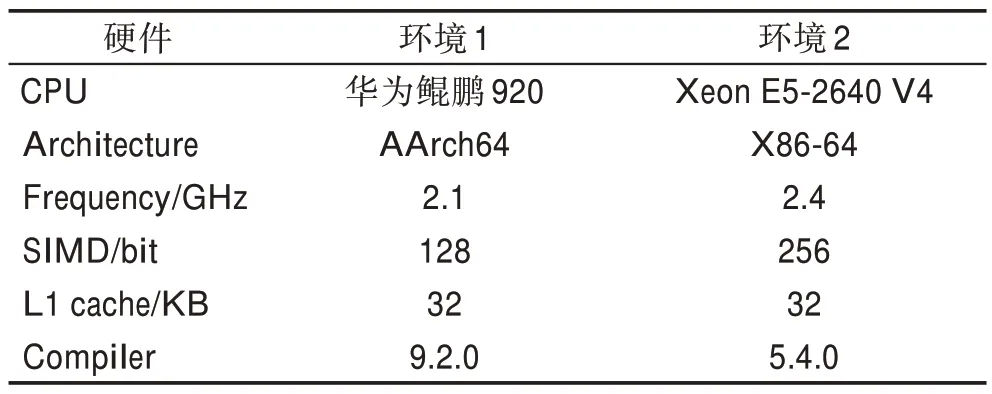
表1 實驗環境Table 1 Experimental environment

4.2 性能分析

本文測試數據維度為一維，數據規模為14×20×（以下性能分析圖橫坐標），輸入輸出均為復數序列。性能評估以每秒所執行的浮點次數（giga floating-point operation per second，Gflops）為單位（以下性能分析圖縱坐標）。

圖8給出了OpenFFT、ARMPL和FFTW在ARMv8體系結構上的一維C2C 的性能。對于單精度和雙精度序列，OpenFFT 算法庫的性能整體高于FFTW 和ARMPL 兩個算法庫。

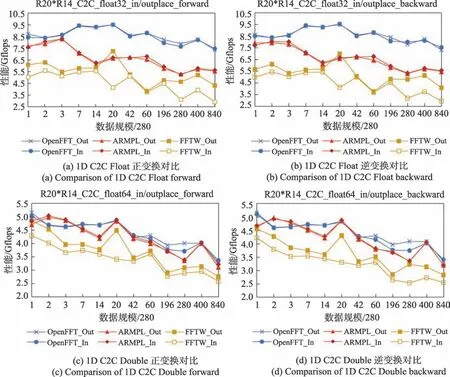
圖8 ARM 1D C2C FFT 性能對比Fig.8 Performance comparison of ARM 1D C2C FFT

（1）單精度Float

如圖8（a）所示，OpenFFT 在ARMv8 下一維C2C FFT 變換優化結果中，相對于ARMPL 實現了平均31.90%的加速比，最大加速比為51.00%，最小加速比為3.58%；相對于FFTW 實現了平均95.50%的加速比，最大加速比為145.80%，最小加速比為31.00%。圖8（b）所示相對于ARMPL 實現了平均32.00%的加速比，最大加速比為51.00%，最小加速比為4.00%；相對于FFTW 實現了平均98.00%的加速比，最大加速比為155.00%，最小加速比為36.10%。

通過比較OpenFFT、ARMPL、FFTW 性能曲線，三者在性能走勢上大致相同，從圖8（a）、圖8（b）可知，OpenFFT 性能在輸入規模為5 600 時，開始下降，主要原因在于，數據規模較小時，數據可存儲在Cache中，增加了Cache 命中率，減少了訪存開銷，導致小規模性能整體高于大規模。

（2）雙精度Double

如圖8（c）所示，OpenFFT 在ARMv8 下一維C2C Double FFT 變換優化結果中，相對于ARMPL 實現了平均4.30%的加速比，最大加速比為19.10%，最小加速比為1.81%；相對于FFTW 實現了平均27.90%的加速比，最大加速比為42.80%，最小加速比為2.90%。圖8（d）所示相對于ARMPL 實現了平均5.36%的加速比，最大加速比為22.20%，最小加速比為0.70%；相對于FFTW 實現了平均35.00%的加速比，最大加速比為47.60%，最小加速比為8.00%。

從圖8 可知，雙精度加速性能相對于單精度要低。主要原因在于SIMD 優化，雙精度Double 為64位，ARM 浮點寄存器為128 位，只能循環展開2 次，寄存器一次處理兩個數據；再有ARM 部分Double 浮點數指令性能低。圖8（c）、圖8（d）在數據規模為560、840 存在性能低于ARMPL 的情況，原因在于Cache命中率低，訪存開銷大且延遲高，再有數據預取不恰當，這些都有可能造成性能不高。

圖9 給出了OpenFFT、MKL 和FFTW 在X86-64體系結構上的一維C2C 的性能。對于單精度和雙精度序列，OpenFFT 算法庫的性能同樣整體高于FFTW和MKL 兩個算法庫。

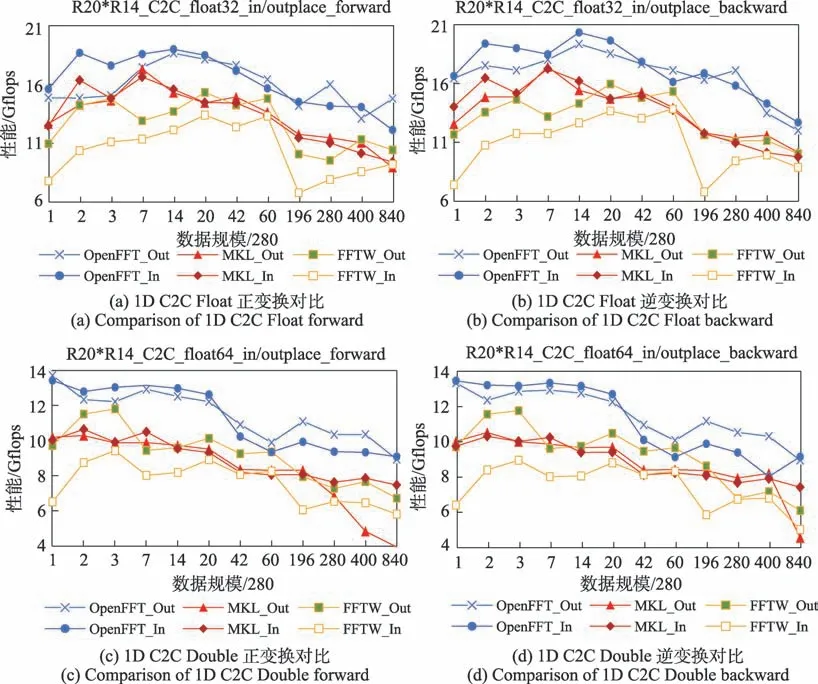
圖9 X86-64 1D C2C FFT 性能對比Fig.9 Performance comparison of X86-64 1D C2C FFT

（1）單精度Float

如圖9（a）所示，OpenFFT 在X86-64 下一維C2C FFT變換優化結果中，相對于MKL實現了平均26.00%的加速比，最大加速比為76.00%，最小加速比為0.92%；相對于FFTW 實現了平均70.00%的加速比，最大加速比為155.00%，最小加速比為3.60%。圖9（b）所示相對于MKL 實現了平均29.40%的加速比，最大加速比為55.20%，最小加速比為3.60%；相對于FFTW 實現了平均81.80%的加速比，最大加速比為175.00%，最小加速比為11.10%。

通過比較OpenFFT、MKL、FFTW 性能曲線，三者在性能走勢上大致相同，OpenFFT 性能走勢最高，其次是MKL，性能最低的是FFTW。從圖9（a）、圖9（b）可知，OpenFFT 性能在輸入規模為3 920 時達到最高點，隨后隨著規模的變大整體性能略下降后趨于穩定。小規模性能高在于數據能存在Cache 中，增加了Cache命中率，因此小規模性能整體高于大規模。

（2）雙精度Double

如圖9（c）所示，OpenFFT 在X86-64 下一維C2C Double FFT 變換優化結果中，相對于MKL 實現了平均45.00%的加速比，最大加速比為126.00%，最小加速比為18.80%；相對于FFTW 實現了平均50.50%的加速比，最大加速比為113.00%，最小加速比為6.50%。圖9（d）所示相對于MKL 實現了平均33.80%的加速比，最大加速比為96.00%，最小加速比為1.50%；相對于FFTW 實現了平均52.70%的加速比，最大加速比為110.00%，最小加速比為2.98%。

表2 總結了在ARMv8 和X86-64 架構在數據規模為14×20×一維C2C 復數序列下，OpenFFT 分別與FFTW、ARMPL 和MKL 算法庫性能對比的平均加速和最大加速。實驗表明OpenFFT 性能明顯優于FFTW、ARMPL 和Intel MKL FFT 算法庫。

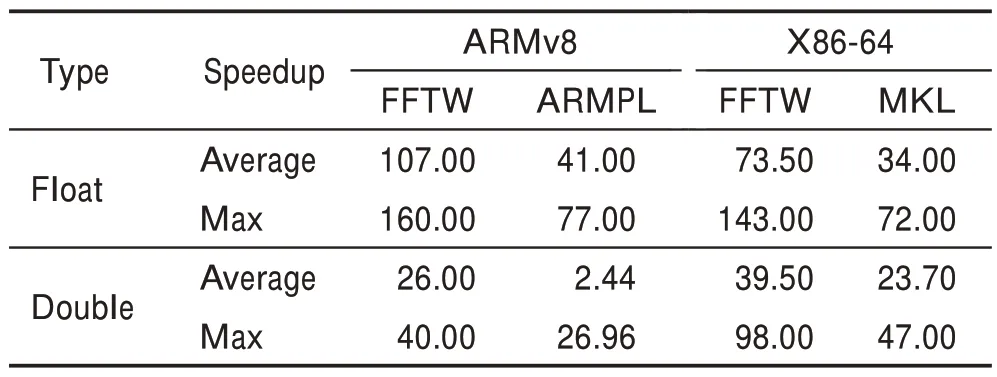
表2 OpenFFT 平均和最大加速Table 2 Average and maximum speedups of OpenFFT %

圖10、圖11 給出了OpenFFT 在ARMv8 體系結構和X86-64 體系結構上同一數據規模大基Radix-14、Radix-20 和中小基Radix-10、Radix-7 等一維C2C性能對比。對于單精度和雙精度序列，同一數據規模OpenFFT 大基性能總體優于小基性能，大基對于總體性能的提升大于大基帶來的性能損耗。

（1）ARMv8 大小基性能對比

①Float 如圖10（a）所示，OpenFFT 在ARMv8 下單精度一維大基C2C FFT 變換，相對于小基實現了平均0.16%的加速比，最大加速比為8.70%；大基跟小基在性能走勢上大致相同，在數據規模達到54 880性能優于中小基。從圖10（a）可知，大基在輸入規模為560、840、11 760、16 800，即為Radix-2 或Radix-3時，性能低于中小基，主要原因是ARM 體系結構單精度下Radix-2、Radix-3 對性能的影響，數據規模分解方式不唯一，ARM 單精度下異常性能的數據規模Radix-20*Radix-14*Radix-2 或Radix-3 不是最優分配造成的性能差異。

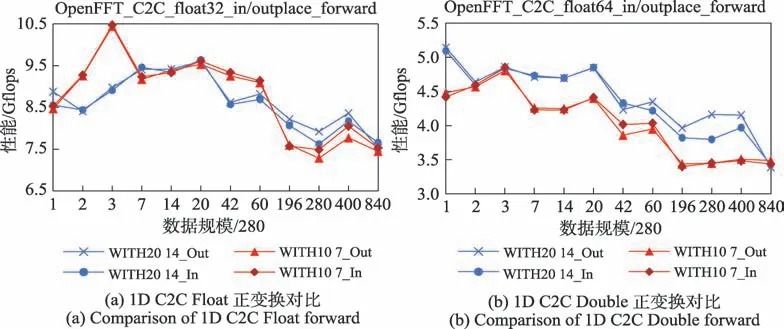
圖10 ARMv8 1D C2C FFT 性能對比Fig.10 Performance comparison of ARMv8 1D C2C FFT

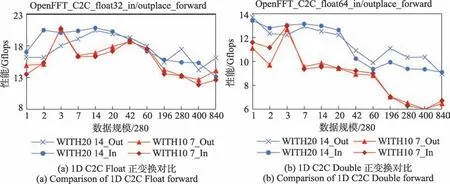
圖11 X86-64 1D C2C FFT 性能對比Fig.11 Performance comparison of X86-64 1D C2C FFT

②Double 如圖10（b）所示，OpenFFT 在ARMv8下雙精度一維大基C2C FFT 變換，相對于中小基實現了平均10.00%的加速比，最大加速比為20.70%；大基跟中小基相比，性能優于中小基。

（2）X86-64 大小基性能對比

①Float 如圖11（a）所示，OpenFFT 在X86-64 下單精度一維大基C2C FFT 變換，相對于小基實現了平均17.00%的加速比，最大加速比為35.90%；大基性能優于中小基，在數據規模超過16 800，大基性能優勢再次拉大。

②Double如圖11（b）所示，OpenFFT 在X86-64 下雙精度一維大基C2C FFT 變換，相對于中小基實現了平均33.30%的加速比，最大加速比為72.80%；大基跟中小基相比，性能優于中小基，性能優勢明顯。

實驗結果表明，大基雖然存在寄存器不夠使用，計算復雜的問題，一定程度上降低了蝶形計算性能，但大基減少了計算過程中的訪存，一定程度提升了性能，大基性能增益明顯大于性能的損耗。

5 結束語

本文在原有FFT 基礎上，通過蝶形網絡優化、大基網絡級數降低減少訪存、大基蝶形計算優化、SIMD 優化寄存器分配等優化方式，突破了快速傅里葉變換在ARMv8 與X86-64 硬件平臺上的算法性能，形成了一套FFT 算法在ARMv8 及X86 架構上的實現策略和優化方案，實現了一個跨平臺的高性能FFT 算法庫。同時對ARMv8 及X86-64 平臺上程序優化提供了思路。下一步的工作將實現和優化快速傅里葉變換列主序，完善OpenFFT 高性能算法庫，形成一套實用完善的高性能FFT 算法庫。