球對稱區域上分數階擴散方程逆源問題

耿肖肖， 程浩， 朱承澄

江南大學 理學院，江蘇 無錫 214122

分數階微分方程越來越受到人們的關注，其主要原因是分數階模型廣泛應用于金融統計、粘彈性力學、反常擴散等研究領域中[1].與整數階微分方程相比，分數階微分算子由于其非局部性質，能夠更精準地描述物理現象.目前，關于分數階擴散方程正問題的研究，不管是在理論還是數值上都已經有了很多有價值的研究成果[2-4].反問題上的研究相對較少，不過最近幾年也得到越來越多的關注，例如反向問題[5-8]、柯西問題[9-10]、逆源問題[11-14]、反演擴散系數問題[15]等等.逆源問題是反問題研究中的一個重要分支，在現實生活中，它也是一類很有應用背景的問題，比如環境污染源的確定、裂縫的識別、新能源的尋找等等.

本文考慮如下球對稱區域上分數階擴散方程：

(1)

若源項F(r，t)、初始條件φ(r)和邊界條件已知，則上述初邊值問題是經典的正問題.

本文所要研究的逆源問題是：假如初始條件和邊界條件已知，通過附加的終值數據

u(r，T)=g(r)，0≤r≤R

來辨識具有變量分離形式的源項F(r，t)=f(r)q(t)中的f(r)，其中q(t)是已知的.

在實際問題中，g(r)是通過測量得到的，帶有一定的誤差，故假設終值數據g(r)和測量數據gδ(r)滿足

‖g(r)-gδ(r)‖≤δ

(2)

其中‖·‖是L2([0，R]，r2)范數，δ>0是測量誤差.眾所周知，逆源問題是不適定的，目前已有很多正則化方法被提出來處理此類問題[17-20].

本文組織結構如下：第1節提供了一些輔助知識；第2節分析了問題的不適定性以及條件穩定性；第3節給出了迭代正則化方法，并獲得了兩種正則化參數選取規則下的誤差估計；第4節通過兩個算例驗證了該方法的有效性；最后一節給出了簡單的結論.

1 輔助知識

定義1對任意常數α>0和β∈R，Mittag-Leffler函數定義為

引理2[22]如果q(t)∈C[0，T]滿足：對?t∈[0，T]，都有q(t)≥q0>0，令

則有

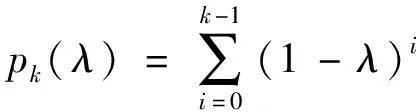
pk(λ)λμ≤k1-μ0≤μ≤1

(3)

rk(λ)λv≤θv(k+1)-v

(4)

其中

2 不適定性與條件穩定性

假如初邊值條件和源項都是已知條件，則通過分離變量法以及Mittag-Leffler函數的Laplace變換可得到正問題(1)的解u(r，t)如下

利用終值數據u(r，T)=g(r)可得

(5)

其中gn=(g(r)，ωn(r)).

記

hn=gn-φnEα，1(-λnTα)

可知算子K是一個具有奇異值

和特征函數ωn(r)的線性自伴算子.根據ωn(r)的性質，式(5)可改寫為

所以有

(6)

根據引理2可知

這表明終值數據g(r)中的微小擾動都會導致源項f(r)發生巨大變化，亦即該逆源問題是不適定的.因此需要通過正則化方法來恢復解的穩定性.

為了保證解的穩定性，假設源項f(r)滿足先驗界條件

‖f(·)‖p≤E，p>0

(7)

這里范數‖f(·)‖p的定義為

定理1若f(r)滿足‖f(·)‖p≤E，則有

其中

證由H?lder不等式和式(6)，有

(8)

根據引理2，則有

(9)

所以由式(8)，(9)可得

注1根據定理1的證明，可以類似得到

這意味著可以通過估計‖f‖p和‖Kf‖的L2范數來得到f的L2范數的界.

3 迭代正則化方法和誤差估計

本節將通過迭代正則化方法求得源項f(r)的正則近似解，并分別給出先驗和后驗參數選取規則下精確解與正則近似解之間的誤差估計.

我們通過構造如下正問題來逼近原來的逆源問題，這里uk(r，t)是如下問題的解

其中源項fk，δ(r)通過下面的迭代方式給出，

f0，δ(r)=0，fk，δ(r)=fk-1，δ(r)-s(uk-1，δ(r，T)-gδ(r))k=1，2，3，…

(10)

這里s是一個加速因子，它滿足：對?n∈N，有

k是迭代步數，它相當于正則化參數.

不妨記

則易得

根據式(10)有

(11)

3.1 先驗誤差估計

定理2設f(r)是逆源問題的精確解，fk，δ(r)是由式(11)給出的正則近似解，若先驗界條件(7)和假設(2)都成立，并選取正則化參數

(12)

則可得到如下誤差估計

證由三角不等式，有

‖fk，δ(r)-f(r)‖≤‖fk，δ(r)-fk(r)‖+‖fk(r)-f(r)‖

根據式(11)，(2)和(3)，并取μ=0，可得

(13)

(14)

結合式(13)和(14)，并選取

即可得到

3.2 后驗誤差估計

設τ>1為給定的常數，正則化參數k的取法是滿足下面偏差原理

‖Kfk，δ(r)-hδ(r)‖≤τδ<‖Kfk-1，δ(r)-hδ(r)‖

(15)

定理3設f(r)是逆源問題的精確解，fk，δ(r)是由式(11)給出的正則近似解，若先驗界條件(7)和假設(2)都成立，且正則化參數k由式(15)取定，則可得到如下誤差估計

證由三角不等式，有

‖fk，δ(r)-f(r)‖≤‖fk，δ(r)-fk(r)‖+‖fk(r)-f(r)‖

由式(13)知

‖fk，δ(r)-fk(r)‖≤skδ

(16)

由式(15)可得

故有

(17)

將式(17)代入式(16)，得

(18)

另一方面，

根據f(r)的先驗界條件以及范數‖f(·)‖p的定義，有

應用注1，可得

(19)

結合式(18)和式(19)，即可得到所要結果.

4 數值算例

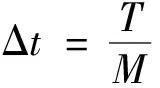
時間項導數可以通過Caputo分數階導數的L1插值逼近來近似得到

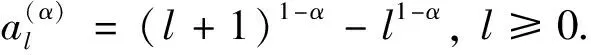
空間項導數由如下格式近似得到

對有限差分得到的終值數據g(r)按如下方式添加隨機擾動得到噪聲數據：

gδ=g+εg·(2rand(size(g))-1)

其中ε>0反映相對誤差水平，相應的噪聲水平為δ=‖gδ-g‖.

為了說明正則近似解的精確性，我們計算絕對誤差

e(f，ε)=‖fk，δ(r)-f(r)‖

和相對誤差

例1取函數q(t)=2t+π，φ(r)=sin(r)，精確的源項為

f(r)=2sin(πr)

圖1和圖2分別給出了先驗和后驗正則化參數選取規則下，取α=0.2，0.8時不同誤差水平下的正則近似解與精確解的數值結果.在表1和表2中，我們分別給出先驗和后驗規則下ε=0.01，α取不同值時精確解與正則近似解之間的誤差分析以及α=0.5，ε取不同值時精確解與正則近似解之間的誤差分析.

圖1 先驗參數選取規則下例1的精確解與正則近似解比較

圖2 后驗參數選取規則下例1的精確解與正則近似解比較

表1 例1關于不同α的數值結果(ε=0.01)

表2 例1關于不同ε的數值結果(α=0.5)

例2取函數q(t)=t+6π，φ(r)=r2-4r，精確的源項為

在圖3和圖4中，我們分別給出了先驗和后驗規則下，取α=0.2，0.8時不同誤差水平下的正則近似解與精確解之間的數值結果.在表3和表4中，我們分別給出先驗和后驗規則下，ε=0.01，α取不同值時精確解與正則近似解之間的誤差分析以及α=0.5，ε取不同值時精確解與正則近似解之間的誤差分析.

圖3 先驗參數選取規則下例2的精確解與正則近似解比較

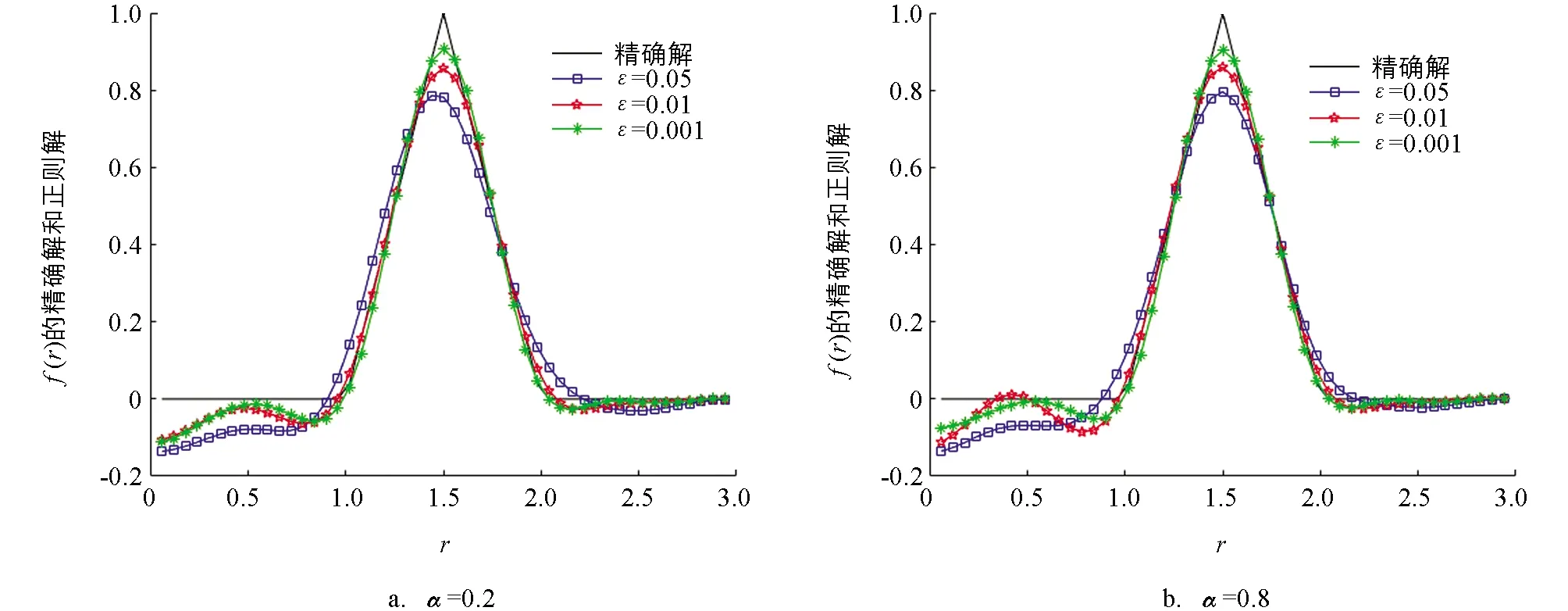
圖4 后驗參數選取規則下例2的精確解與正則近似解比較

表3 例2關于不同α的數值結果(ε=0.01)

表4 例2關于不同ε的數值結果(α=0.5)

綜合對比圖1至圖4，可以看出，后驗正則化參數選取規則下重構的源項與精確解之間的擬合效果總體要比先驗的好一些.再結合表1至表4，可以發現數值誤差關于α變化比較穩定，故我們的方法對α不太敏感(這與文獻[20]的結果相符)，同時也可以發現隨著隨機擾動ε的減小，數值誤差明顯在減小，精確解與正則近似解也越來越吻合.這說明對于球對稱區域上分階擴散方程的逆源問題，采用該迭代正則化方法有著非常好的效果.

5 結論

探討了球對稱區域上分數階擴散方程逆源問題.通過迭代正則化求得源項的正則近似解，并在先驗和后驗參數選取規則下給出了精確解與正則近似解之間的H?lder型誤差估計.最后，通過數值算例驗證了該迭代方法處理此逆源問題的有效性.