具有弱依賴組的復雜網絡上的級聯失效*

潘倩倩 劉潤然 賈春曉

(杭州師范大學,復雜科學研究中心,杭州 311121)

1 引言

真實世界中的許多復雜系統都可以抽象成復雜網絡,如常見的交通網絡[1-4]、電力網絡[5]、社交網絡[6]、疾病傳播網絡[7,8]和生物網絡[9,10]等.在復雜系統魯棒性的研究中,人們常常借助于復雜網絡級聯失效模型對復雜系統的崩潰過程進行建模和研究,節點的失效不僅會對網絡整體的連通性造成影響,也可能會因節點之間的依賴關系而引起失效在網絡中蔓延.最初復雜網絡魯棒性的研究是將兩種效應分開進行的,即針對網絡節點之間的連接關系來探討網絡在失去部分連接或節點之后的連通性[11-13],以及節點間的耦合或依賴性所引起的失效節點的雪崩或級聯效應[14].對于前者,人們借助于滲流模型發現,隨機網絡發生滲流相變的臨界點與網絡平均度呈反比關系[15];無標度網絡具備“魯棒性和脆弱性共存”的特征[16-18],即對隨機故障的魯棒性較強,但面對蓄意攻擊時則顯得十分脆弱;對于小世界網絡,“捷徑”使得網絡的魯棒性增強[19],但也更容易在蓄意攻擊下破碎[20].對于復雜網絡級聯失效的研究,如何對節點之間的耦合和依賴進行建模是一個核心問題.研究人員考慮了真實復雜系統的特征,主要考慮了動態負載分配、局部依賴和依賴組的引入等幾個方案.

1) 動態負載分配[21-27].當網絡中部分節點失效后,網絡節點之間最短路徑的分布發生較大的變化,網絡中信息或能量的流動路徑就會重新分配,從而引起部分節點的運行效率下降[21],甚至過載失效[27].在這類模型中,一個負載較小節點的失效可能不會引起負載失衡并誘發較大范圍的過載故障;而失效節點的負載較大時,這些節點的失效可能會顯著影響其他節點的負載,并引發一系列大范圍的過載故障[23,27].為了探討級聯失效的產生條件并為級聯失效的防御和控制提供思路和策略,節點失效后荷載的分配方案對網絡級聯失效動力學的影響也受到廣泛關注,如隨機荷載再分配機制[28]、基于邊權重的再分配策略[29,30]、供需網絡中的供應策略[31]等.除了流量分配機制外,網絡結構調整策略[32]、攻擊策略[33]、網絡中流量的漲落[34]、網絡的結構特征[35]等因素對于級聯失效的影響也受到廣泛的關注.

2)局部依賴.Watts 模型研究了鄰居中相反狀態節點比例對節點狀態的影響,發現了復雜網絡發生級聯失效的臨界判據[36,37].此外,考慮到網絡高度值互連部分節點(k核)所組成結構的重要性,Dorogovtsev 等[38]提出了k核滲流模型,該模型將通過一個反復迭代的剪枝過程獲得的最小度為k的節點所形成的連通子圖視為k核.度分布的二階矩有限時,隨著初始刪除節點的增加,k核巨分支在某一臨界點會突然消失,表現為不連續的混合相變現象.如果度分布的第二階矩發散,則網絡包含一個無限序列的k核,這些k核對隨機攻擊具有很強的魯棒性.類似地,靴攀滲流模型考慮了失效鄰居的數量對節點狀態的影響,當節點失效鄰居數達到某個閾值時該節點就會失效,研究發現,在不同的度分布情形下,網絡中也會出現一階不連續相變和連續相變的現象[39].

3)依賴組的引入.上述兩種模型中節點都是通過相互鄰接關系進行狀態傳遞的,但現實網絡中不相鄰的節點也可能存在隱含的相互影響.Parshani等[40]考慮到不相鄰節點之間也可能存在依賴性,于是提出了依賴組概念來描述復雜網絡中節點的隱含依賴性,這種依賴組的存在導致網絡能夠發生級聯失效并導致網絡更加脆弱,如在依賴組的密度較高或依賴組規模較大時網絡會在遭受攻擊時以一階不連續相變的方式發生突然性的崩潰[41],同時依賴組的規模和分布[41]以及依賴規則[42-44]等特征的變化對網絡魯棒性和級聯失效有著不同程度的影響.

在關于依賴組的研究中,大多數模型基于一個簡單的假設:一個節點的失效可以直接導致其依賴節點的全部失效,這種“節點對節點”的“強依賴”的假設導致了網絡在遭受攻擊時極為脆弱,這一結果不但與現實中某些觀測不符,也不能充分描述部分復雜系統節點之間的依賴關系[45,46].在現實網絡中,一個節點的失效可能對其依賴節點的一部分功能造成影響,而不是導致其完全失效[47,48].如金融系統中,所屬同一個投資者的公司之間相互依賴,由于風險分散,一家公司的倒閉不太可能直接導致投資者的其他公司全部破產,而現實的情況是,其余公司可能會因現金流的減少而收縮自己的業務.因此與以往模型所描述的“節點對節點”依賴模式不同,在一些普遍場景下系統節點之間的依賴關系體現在“節點對邊”的相互作用上,即一個節點失效后,依賴組內的其余節點會因受到沖擊而損失部分連接.這種描述“節點對邊”的相互作用機制可以描述更為一般化的場景,如屬于同一個依賴組的若干節點,當其中一個節點失效的時候,不會引起其余全部或部分節點立即失效,而是失效節點給剩余依賴節點帶來一定程度的沖擊和影響.

本文引入了“弱依賴組”概念,通過一個可調參數來控制同一依賴組內節點的相互依賴強度并研究依賴組的大小、分布和網絡度分布對網絡的級聯失效的影響.通過理論研究和數值模擬的結果,發現改變依賴組的參數時,網絡能夠發生連續和不連續的兩種滲流相變,且無標度網絡在滲流過程中可能會出現雙重相變現象.

2 具有弱依賴組的網絡級聯失效模型

考慮一個由N個節點通過一些連接邊所組成的網絡,節點的連接度服從概率分布函數P(k)[7],同時網絡中的每一個節點都隨機地與其他節點形成一個包含M個節點的依賴組,組內的節點互相依賴.當依賴組中一個節點失效時,其余節點會受到一定程度的沖擊,影響強度由解耦系數α控制,即其余每個節點的每條邊都以α的概率保留下來,而以 1-α的概率被刪除.參數α在描述失效節點對其余依賴節點所造成破壞性的同時,也描述了一種“節點對邊”的作用機理,在描述依賴節點之間的相互作用上更具有一般性的意義,當α →1 時,依賴組內節點的耦合強度最弱,一個節點的失效不能對組內其余節點造成任何影響,此時模型與普通的座滲流等價;而當α →0 時,依賴組內節點的耦合強度最強,一個節點的失效就能造成組內所有節點全部失效,此時模型與文獻[41]中強依賴組的模型等價.通過調整模型參數α可以研究不同耦合強度對網絡級聯失效動力學和魯棒性的影響[49,50].

網絡級聯失效通過隨機攻擊網絡中比例為1—p的節點來觸發,這些被攻擊節點及其連接被從網絡中全部刪除,進而導致網絡發生破碎.在網絡中,能夠連接到巨分支的節點視為功能節點,其他節點視為失效節點.由于弱依賴組內節點之間存在一定程度的依賴性,網絡中一個節點的失效會造成兩種影響:1)組外影響,節點失效會引起網絡破碎,進而導致組外部分節點不能通過該節點連接到網絡巨分支而失效;2)組內影響,失效節點所在的依賴組內的其余節點會受到損害,其每一條連接邊都以1 —α的概率被刪除,即以α的概率被保留.當一個節點失效后,組外影響導致失效能夠跨依賴組傳播,從而使失效擴展到更大的范圍,而組內影響導致組內的其余節點的邊受到破壞,從而引起組內更多節點失效.在這兩種影響的交替作用下,網絡上的級聯失效就會發生.我們將這兩種擴散過程稱為“組間級聯失效”和“組內級聯失效”.當這兩個過程停止時,網絡不會產生新的失效節點而發生進一步的破碎,所有依賴組內也不會有新的連接邊被刪除,網絡即達到穩態.本文用網絡穩態巨分支的相對大小S來衡量網絡的完整性,隨著初始保留節點比例p的降低,網絡巨分支的大小S會以二階連續相變或一階不連續相變的方式在一個臨界點或處降低至零,二階相變的臨界點或一階相變的臨界點通常用于度量網絡的魯棒性[15,51,52].

圖1 為具有弱依賴組的網絡的級聯失效示意圖.圖中虛線橢圓內的節點形成一個依賴組,實線表示網絡內功能正常的連接邊,點狀虛線表示被刪除的連接邊;功能正常的節點用綠色標記,失效節點用紅色標記,黃色節點表示功能正常但受到損壞的節點.圖1 中(a)表示的是一個未受到攻擊的網絡;(b)網絡中存在一個最初被刪除的節點2;(c)由于節點2 被刪除,其所有連接邊失效;(d)由于節點1 與網絡巨分支之間的連接邊被移除,導致節點1 脫離網絡巨分支而失效;(e)由于節點7 和節點1 屬于同一個弱依賴組,相互依賴,故節點1的失效會導致節點7 受損;(f)節點7 受到了一定的沖擊,節點7 與節點6 之間的連接邊失效;(g)因節點7 與節點6 之間的連接邊失效,導致節點6 脫離網絡巨分支,發生故障;(h)由于處在同一弱依賴組,節點5,4 受節點6 失效的影響而受損;(i)節點5 受損導致節點3 和節點5 之間的連接邊失效,并且網絡達到了最終的穩定狀態.

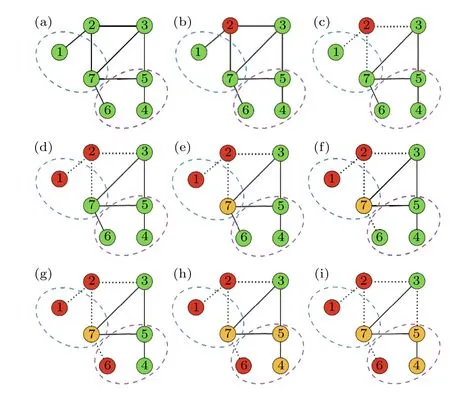
圖1 具有弱依賴組的網絡的級聯失效示意圖Fig.1.Schematic diagram of the cascading process in a network with weak interdependency groups.

3 理 論

用概率生成函數理論來對模型求解.在求解過程中,采用度分布的生成函數來生成網絡的度分布,即一個隨機節點度值為k的概率是P(k);類似地,采用余度分布生成函數來生成一條隨機邊到達一個度值為k的節點的概率,即排除這條隨機邊之外到達節點的余度為k—1的概率[53].在這兩個生成函數中,表示網絡的平均度.為了求解穩態時網絡巨分支的規模,定義R為網絡中任意一條隨機邊能夠連接到巨分支的概率.假定在網絡中隨機挑選一條邊后,沿著這條邊的任意一端可到達一個度值為k的節點i,若該節點所屬依賴組內有t個失效節點,他的每條邊能夠保留下來的概率為αt.由于任意一個節點度值k服從概率分布P(k),節點i的任意一條隨機邊能夠連到巨分支的概率分布遵循根據生成函數G1(x) 并考慮k的概率分布,可將一條隨機邊連接到巨分支的概率簡寫為αt[1-G1(1-αtR)][54,55].如果將任意一個節點所在的依賴組內失效節點數t所服從的概率分布記為f(t),考慮所有可能的t,可以得到R滿足自洽方程:

同理,可以得到一個隨機節點屬于網絡穩態巨分支的概率S的方程:

求解方程(1)和方程(2)需要用到概率分布函數f(t),該函數可以通過概率R來獲得.當網絡處在穩定狀態時,假如隨機選擇一個節點具有t個失效的依賴節點,那么該節點還能保留下來的概率為p[1-G0(1-αtR)],與其同在一個依賴組中的其他M—t—1 個依賴節點全部存活的概率為{p[1-G0(1-αtR)]}M-t-1.此外,依賴組內的失效節點分為兩種,一種是因遭受初始攻擊或因組外節點失效導致其脫離巨分支而失效,另一種是組內其他節點的失效導致其連接的減少而失效.假設有s個節點的失效是由前一種原因造成的,其發生概率為{1-p[1-G0(1-R)]}s,那么t-s個節點的失效是由后一種原因導致的,概率為{p[G0(1-αsR)-G0(1-R)]}t-s.因此,t的概率分布函數f(t) 為

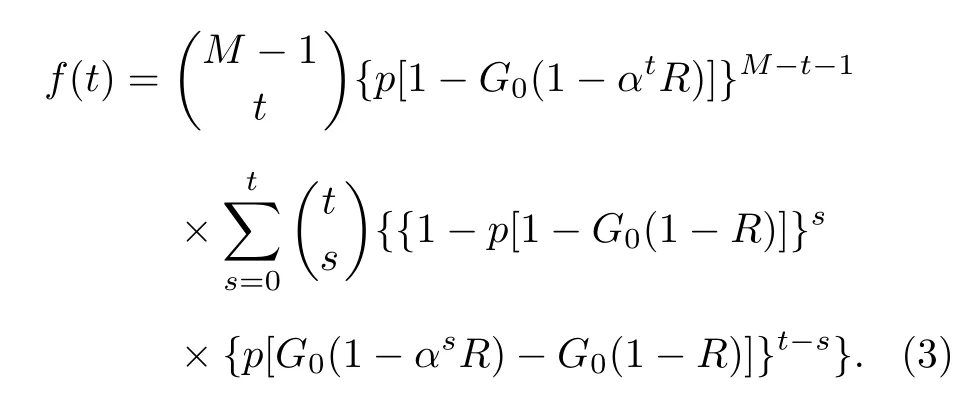
對于給定的度分布P(k)和弱依賴組大小M,結合方程(3)并通過聯立方程(1)和方程(2)可以得到網絡中巨分支的最終大小S.

當α →1 時,依賴組內節點依賴強度趨向0,節點之間無相互依賴性而不會發生級聯失效,隨著保留節點比例p的降低,網絡以二階連續相變的方式發生破碎[15].當α →0 時,弱依賴組內節點之間的依賴強度最強,一旦組內一個節點被刪除,組內其余節點將全部失效,網絡以一階不連續相變的方式發生破碎.因此,弱依賴組內節點之間的依賴強度α的值決定著網絡在遭受攻擊時的破碎形式,當α超過臨界點αc時,網絡的破碎方式可以從二階滲流相變轉變為一階滲流相變.在網絡以二階相變方式發生破碎的情況下,當p接近二階滲流相變點時,隨機邊屬于穩態巨分支的概率R趨于零.在R ≡ε →0 和p →時,可以將(1)式進行泰勒展開表示為

進而可以求出二階滲流相變點:

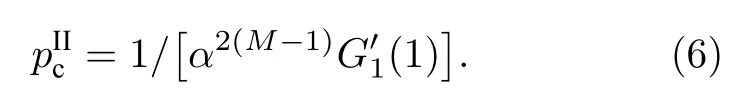
當α=1 或M=1 時,網絡不存在弱依賴組,其結果和普通網絡的滲流結果相同,二階滲流相變點(1)[17].同時還可以發現,二階滲流相變點隨著弱依賴組大小M的增大而減小,這意味著網絡中弱依賴組規模越大,網絡就越脆弱.這一結果與弱依賴多層網絡的結果類似,即二階相變點與網絡的層數和參數α有關[56].

圖2 在不同初始保留節點比例p 和解耦系數α 時(1)式的圖解 (a) α=0.5 的結果;(b) α=0.63 的結果;(c) α=0.8 的結果.本圖中所用網絡的度分布服從冪率分布 P(k)～k-γ(kmin ≤k ≤kmax),其中 kmin=2 ,kmax=141 ,γ=2.3Fig.2.The graphical solutions of Eq.(1) for different values of p and α:(a) Result for α=0.5 ;(b) result for α=0.63 ;(c) result for α=0.8 .For each panel,the degree distribution of networks follows a truncated power-law distributionP(k)～k-γ(kmin ≤k ≤kmax)with kmin=2 ,kmax=141,and γ=2.3 .

通過對(9)式求解,可以得到一階相變和二階相變發生轉變的臨界點αc.在隨機網絡中,節點度值服從泊松分布,方程(9)可以簡化為

從(10)可以看出,αc依賴于網絡平均度和依賴組的規模M.對于無標度網絡,(9)式可以寫成

其中括號〈·〉表示依據度分布對括號內的項取平均.因此,αc不僅取決于依賴組的規模M,而且依賴于無標度網絡的度分布P(k).

4 數值模擬結果與分析

本文選擇了兩種網絡模型,即度分布滿足泊松分布的ER 隨機網絡和度分布滿足近似冪律的無標度網絡,來研究弱依賴組內節點的依賴強度、依賴組的規模和分布等不同特征對網絡級聯失效動力學和魯棒性的影響,并通過理論計算對數值模擬的結果予以驗證.對于ER 隨機網絡,采用隨機向N個節點隨機加邊的方式生成.而對于無標度網絡,首先生成一個近似滿足冪率分布的度序列,然后采用配置模型生成其對應的無標度網絡.在兩種模型的生成過程中,自環和重復連接被禁止.

4.1 弱依賴組規模均勻分布

為了描述具有弱依賴組的網絡上的“組間級聯”和“組內級聯”兩種失效過程對網絡魯棒性的影響,本文以依賴組大小M=3 和M=4 的兩種情況為例,研究當弱依賴組大小均勻分布時網絡級聯失效動力學的特點.圖3(a)和圖3(b)分別給出了當M=3和M=4 時,平均度〈k〉=4 的隨機網絡穩態巨分支的大小S隨初始節點保留概率p的增加而變化情況.圖3(c)和圖3(d)給出了平均度〈k〉=5的隨機網絡,當弱依賴組大小M分別為3 和4 時,網絡穩態巨分支規模S隨p的增加而變化的情況.從圖3(a)和圖3(b)可以發現,無論是M=3還是M=4 的情況,當α較小時,隨著初始保留節點p的降低,網絡都是以一階不連續相變的方式發生崩潰;而對于較大的α值,隨著初始保留節點p的降低,網絡以二階連續相變的形式逐步瓦解.另外,可以發現M=3 的網絡的臨界點小于M=4的網絡的臨界點,這意味著前者比后者具有更強的魯棒性.對于〈k〉=5 的隨機網絡,雖然定量的結果與〈k〉=4 時存在差異,但定性的結果是相似的.這些結果證實了依賴組的規模和組內節點的依賴強度對網絡的破碎形式有著重要影響,依賴組規模越大,網絡的魯棒性就越差,同時依賴強度對網絡的魯棒性也有重要影響,當依賴強度較大時網絡以一階不連續相變的形式發生破碎,而依賴強度較小時網絡以二階連續相變的形式發生破碎.

圖3 依賴組規模 M=3 和 M=4 的隨機網絡上的滲流相變 (a),(b)平均度為 〈k〉=4 的隨機網絡,弱依賴組大小分別為M=3和 M=4 的結果;(c),(d)在 〈k〉=5 時,弱依賴組平均大小分別為 M=3 和 M=4 的隨機網絡的結果.圖中網絡規模N=105,實線表示由(1)式和(2)式得到的理論預測,而垂直虛線分別表示由(5)式和(7)式所預測的一階和二階滲流相變點.模擬結果來自于100 次不同初始條件下的平均Fig.3.Simulation results for the percolation transitions on random networks with group sizes M=3 and M=4 :(a),(b) Results for random networks with the interdependency group sizes M=3 and M=4 respectively,where the average degree 〈k〉 is set to 4 for both panels;(c),(d) results for random networks with the interdependency group sizes M=3 and M=4 respectively,where average degree 〈k〉 is set to 5 for both panels.The network size is N=105 .The solid lines behind the symbols denote the theoretical predictions that were obtained by Eqs.(1) and (2).The vertical dashed lines denote the first-order and second-order percolation transition points predicted by Eqs.(7) and (5),respectively.The simulation results were averaged from 100 realizations of different initial conditions.

圖3 還提供了理論預測的結果,理論預測的網絡巨分支規模S與模擬結果非常符合,另外,數值模擬所得到的網絡巨分支的規模S在理論預測的相變點處消失為0.這些結果證實了本文理論的正確性.此外,在不同初始條件下,初始節點保留概率p值對于極大簇的規模分布有著非常重要的影響.在p值遠離臨界點時,極大簇的規模分布是非常均勻的,而在p值處于臨界點附近時,極大簇規模的漲落會非常大.因此除了理論預測的方法之外,還可以通過數值模擬來獲得極大簇方差的大小來定位網絡發生破碎的臨界點[47].

圖4 給出了弱依賴組大小分布均勻時,無標度網絡的巨分支規模S隨初始保留節點比例p的變化.此時,網絡節點度服從P(k)～k-γ(kmin≤k≤kmax),其中kmax和kmin分別是節點度的上下限,γ是冪律指數,其平均度.與ER 隨機網絡的結果類似,對于較小的α值,網絡以一階不連續的方式發生崩潰,對于較大的α值,網絡以二階連續的方式逐步瓦解.兩種滲流相變形式由臨界點αc隔開.且當M=3 時,網絡的滲流相變點小于M=4 的網絡的滲流相變點,這意味著M=3的網絡比M=4 的網絡具有更強的魯棒性.有趣的是,我們還發現當α增大到一定程度時無標度網絡會發生雙重相變,如α=0.63 .對于雙重相變,網絡首先以二階連續相變的方式滲流,然后隨著p的增加又會發生一階不連續相變.隨著α的增加,網絡破碎形式轉變為單個二階連續相變;隨著α的減小,二階連續相變消失,網絡的破碎形式轉變為單個一階不連續相變.

圖4 依賴組規模 M=3 和 M=4 的無標度網絡滲流相變 (a),(b)在 〈k〉=4 (kmin=2 ,kmax=63,γ=2.5)時,弱依賴組平均大小分別為 M=3 和 M=4 時的結果;(c),(d)在 〈k〉=5 (kmin=2 ,kmax=141 ,γ=2.3)時,弱依賴組規模分別為M=3和 M=4 時的結果.網絡規模 N=105 .圖中實線表示由(1)式和(2)式得到的理論預測.垂直虛線分別表示(7)式和(5)式預測的一階和二階滲流相變點.模擬結果來自于100 次不同初始條件下的平均Fig.4.Simulation results for the percolation transitions on scale-free networks with the interdependency group sizes M=3 and M=4:(a),(b) Results for scale-free networks withthe interdependency group sizes M=3 and M=4 respectively,where the average degree 〈k〉 is 4 with kmin=2,kmax=63 and γ=2.5 ;(c),(d) results for scale-free networks with the interdependency group sizes M=3 and M=4 respectively,where the average degree 〈k〉 is 5 with kmin=2,kmax=141 and γ=2.3 .The network sizeis N=105 .The solid lines behind the symbols denote the theoretical predictions by Eqs.(1) and (2),and the vertical dashed lines denote the first-order or second-order percolation transition points predicted by Eqs.(7) and (5),respectively.The simulation results are averaged from 100 realizations of different initial conditions.

此外,圖4 的結果還表明,雙重相變發生于度分布異質性較強的無標度網絡且依賴組內節點依賴強度適中時.這是由于無標度網絡節點的度分布異質性較強,當網絡受到攻擊而發生級聯失效時,較多度值較小的節點會率先脫離網絡的巨分支而失效,當失效節點的規模發散時網絡就會發生一階不連續的相變,而此時網絡中度值較大的節點仍然能夠形成穩定的簇結構,需要更大的攻擊強度才能夠將其徹底破壞.當依賴組中節點的依賴強度較大時,度值較大的中心節點很容易受到度值較小節點的影響而失效,無法形成規模較大的簇結構來對抗級聯失效,此時網絡只能發生一階相變;在當依賴組中節點的依賴強度較弱時,節點會因相互之間的依賴太弱無法形成較大規模的級聯失效而發生二階連續相變.

圖5(a)和圖5(b)分別給出了在M=3 和M=4時隨機網絡的滲流相變點pc隨α變化的情況,其中不同顏色的曲線表示不同網絡平均度的結果.圖中αc表示一階相變和二階相變的轉變點,其值由弱依賴組的大小M和網絡平均度〈k〉決定.圖5(c)和圖5(d)分別給出了在M=3 和M=4 時無標度網絡的滲流相變點隨α的變化.

圖5 隨機網絡和無標度網絡在弱依賴組規模服從平均分布時滲流相變點 pc 與α 的關系 (a)依賴組規模 M=3 的隨機網絡的滲流相變點 或與α 的關系,其中平均度 〈k〉 為4,5 和6;(b)依賴組規模 M=4 的隨機網絡的結果;(c)平均度 〈k〉 為4,5 和6 (分別對應度分布的冪律指數 γ 為2.5,2.3 和2.1)且依賴組規模 M=3 的無標度網絡的結果;(d)依賴組規模 M=4 的無標度網絡的結果.圖中實線為一階滲流相變點,虛線為二階滲流相變點 .模擬結果來自于100 次不同初始條件下的平均Fig.5.The percolation transition point pc as functions of αon random networks and scale-free networks with uniform interdependency group size:(a) Results for random networks with the interdependency group size M=3,where the average degree 〈k〉 is 4,5 and 6 from high to low;(b) results for random networks with the group size M=4,where the average degree 〈k〉 is 4,5 and 6 from high to low;(c) results for scale-free networks with thegroup size M=3,where the average degree 〈k〉 is 4,5 and 6 (corresponding to a power-law exponent of degree distribution γ is 2.5,2.3 and 2.1,respectively);(d) results for scale-free networks with the interdependency group size M=4,where the average degree 〈k〉 is 4,5 and 6.The solid line is the first-order percolation transition point ,and the dashed line is the second-order percolation transition point .The simulation results were averaged from 100 realizations of different initial conditions.

從中可以發現,相變的方式以αc為界分為不連續和連續兩種,但αc的值取決于弱依賴組的大小M和網絡度分布P(k).另外,當無標度網絡出現雙重相變情況時,網絡先以二階連續相變的方式滲流,因此網絡滲流相變點為二階相變點.同時也可以發現,在大多數情況下,當依賴組內節點依賴強度較弱時,隨機網絡魯棒性比無標度網絡差,而當依賴組內節點依賴強度較強時,無標度網絡魯棒性比隨機網絡差.這是由于在隨機攻擊時,無標度網絡中度值較大的中心節點不容易受到攻擊,在依賴組內節點依賴強度較弱時也不容易受到其他節點的影響而受到損害,然而在依賴強度較大時,無標度網絡中度值較大的節點容易受到組內其他節點失效的影響而造成大量連接被刪除,從而對網絡整體的連通性造成較大的影響.這一結果表明,無標度網絡的魯棒性與依賴組內節點的依賴強度有著密切的關聯.

4.2 弱依賴組大小泊松分布

考慮到現實中一些復雜系統節點所形成的依賴組的規模并不一定是均勻的,本節以弱依賴組規模服從泊松分布的情況為例,用ER 隨機網絡和無標度網絡來研究弱依賴組規模的非均勻分布對網絡級聯失效動力學的影響.考慮弱依賴組規模服從泊松分布函數Q(M=i)=,i=1,2,···,Mmax,其中〈M〉表示依賴組的平均規模.此時方程(1) 轉換成

全國家用電器工業信息中心是面向全國家用電器行業服務的專業信息機構，擁有強大的行業研究、技術研究、標準研究和信息處理能力。全方位地提供行業分析、企業分析、市場分析及預測、預警等方面服務，在家電行業極具影響力。全國家用電器工業信息中心總部位于北京。

同理,方程(2)要轉換成

關于滲流相變點的求值與上文所述的弱依賴組平均分布的求值方法相同,可得到二階滲流相變點:

根據方程(14)可以發現,當網絡中弱依賴組規模分布服從泊松分布時,網絡的二階滲流相變點與依賴組平均規模〈M〉相關,二階滲流相變點隨著弱依賴組平均規模〈M〉的增大而減小,這意味著網絡中弱依賴組平均規模越大,網絡魯棒性就越差.

當網絡發生一階滲流相變時,R在相變點處從零跳躍到一個非零值Rc,此時方程(7)同樣成立,通過聯立方程(7) 和方程(12)求得弱依賴組規模服從泊松分布時的一階滲流相變點

與弱依賴組規模平均分布時一階與二階滲流相變的臨界點αc滿足的條件相同,當p →pc和α=αc時,h′′(0)=0,此時得到

在度分布服從泊松分布的隨機網絡中,方程(15)可簡化為

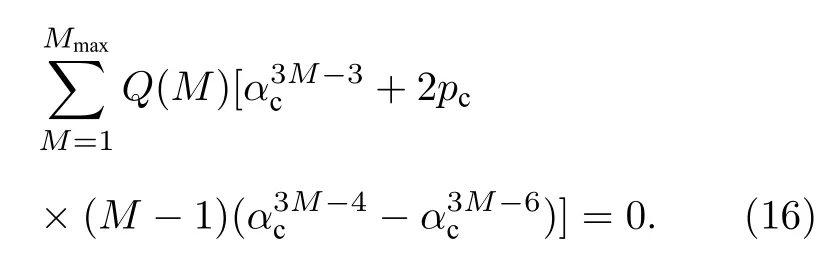
在度分布近似冪率分布的無標度網絡中,方程(15)可簡化為

圖6(a)和圖6(b)分別給出了弱依賴組規模服從泊松分布且平均值〈M〉分別為3 和4 時,平均度〈k〉=4隨機ER 網絡穩態巨分支的大小S隨p增加而變化的情況.圖6(c)和圖6(d)分別給出了弱依賴組規模服從泊松分布且平均值〈M〉分別為3 和4 時,平均度〈k〉=5 的隨機網絡穩態巨分支的大小S隨p增加而變化情況.從圖中可以發現在隨機網絡中,對于較小的α值,網絡以一階不連續相變方式滲流,對于較大的α值,網絡以二階連續相變方式滲流.兩種相變的形式在臨界點αc處發生改變.另外,可以發現〈M〉=3 時,網絡滲流相變點小于〈M〉=4 的網絡,這意味著依賴組平均規模較小的網絡魯棒性更強.當〈k〉=5 時,弱依賴組平均規模〈M〉=3和〈M〉=4 的隨機網絡也具備類似的現象.圖6 還提供了理論預測,結果與模擬結果基本符合.

圖6 弱依賴組平均規模 〈M〉=3 和 〈M〉=4 的隨機網絡滲流相變的模擬結果 (a),(b) 平均度 〈k〉=4 的ER 隨機網絡在依賴組平均規模分別為 〈M〉=3 和 〈M〉=4 時的結果;(c),(d)平均度 〈k〉=5 的ER 隨機網絡在依賴組平均規模分別為 〈M〉=3 和〈M〉=4時的結果.網絡規模設為 N=105 .圖中實線表示由(12)式和(13)式得到的理論預測.垂直虛線分別表示理論預測的一階和二階滲流相變點.模擬結果來自于100 次不同初始條件下的平均Fig.6.Simulation results for percolation transitions on random networks with average group sizes 〈M〉=3 and 〈M〉=4 :(a),(b) Results for random networks with the average group sizes 〈M〉=3 and 〈M〉=4,respectively,where the average degree 〈k〉 is 4 ;(c),(d) results for random networks with the average group sizes〈M〉=3 and 〈M〉=4 respectively,where 〈k〉 is 5.The network size is N=105 .The solid linesbehind the symbols denote the theoretical predictions that were obtained by Eqs.(12) and(13),and the vertical dashed lines denote the first-order and second-order percolation transition points predicted by theory.The simulation results were averaged from 100 realizations of different initial conditions.

圖7 給出了弱依賴組大小分布為泊松分布Q(M),且規模平均值〈M〉=5 和〈M〉=6 時,無標度網絡上的滲流相變.從圖7 可以發現類似于隨機網絡的結果,對于較小的α值,網絡以一階不連續相變方式滲流,對于較大的α值,網絡以二階連續相變方式滲流.兩種滲流相變的形式的轉變點發生于αc處,且〈M〉=5 的網絡的滲流相變點小于〈M〉=6的網絡,這意味著前者比后者具有更強的魯棒性.同時發現,當弱依賴組大小服從泊松分布時,無標度網絡的雙重相變現象依然存在.圖7 還提供了理論預測,理論結果與模擬結果的誤差相對于隨機網絡較大,主要存在兩個原因.首先對于無標度網絡在給定度序列的情況下,由于度值較大的節點的數量較小,但這些節點對網絡的魯棒性產生了非常關鍵的作用,不同網絡連接結構的差異性會對模擬結果產生較大的影響,因此模擬結果的誤差較大.第二,極大簇在相變點附近有較大的漲落,也會導致模擬結果存在一定的誤差.

圖7 弱依賴組平均規模 〈M〉=5 和 〈M〉=6 的無標度網絡滲流相變的模擬結果 (a),(b)在 〈k〉=4,即 kmin=2 ,kmax=63,γ=2.5時,弱依賴組平均規模分別為 〈M〉=5 和 〈M〉=6 的結果;(c),(d) 在 〈k〉=5,即 kmin=2,kmax=141,γ=2.3 時,弱依賴組平均規模分別為 〈M〉=5和 〈M〉=6 的結果.網絡規模為 N=105 .圖中實線表示由(12)式和(13)式得到的理論預測.垂直虛線分別表示預測的一階和二階滲流相變點Fig.7.Simulation results for percolation transitions on scale-free network with average group sizes 〈M〉=5 and 〈M〉=6 :(a),(b)Results for scale-free networks with average group sizes 〈M〉=5and 〈M〉=6 respectively,where the average degree 〈k〉 is 4 with kmin=2 ,kmax=63 and γ=2.5 ;(c),(d) results for scale-free networks with 〈M〉=5 and 〈M〉=6 respectively,where〈k〉is 5 with kmin=2 ,kmax=141 and γ=2.3 .The network size is N=105 .The solid lines behind the symbols denote the theoretical predictions by Eqs.(12)and (13),and the vertical dashed lines denote the first-order and second-order percolation transition points predicted by theory.The simulation results were averaged from 100 realizations of different initial conditions.

圖8(a)和圖8(b)分別給出了當網絡平均度〈k〉不同時,弱依賴組平均規模〈M〉=3和〈M〉=4的隨機網絡的滲流相變點pc隨α的變化.圖中網絡滲流相變的形式在αc處發生改變,且αc的大小由弱依賴組平均規模〈M〉和隨機網絡的平均度〈k〉決定.圖8(c)和圖8(d) 分別給出了不同平均度〈k〉時,弱依賴組平均大小〈M〉=3 和〈M〉=4 無標度網絡的滲流相變點pc隨α的變化.從中也可以發現類似依賴組大小平均分布的相變情況,相變的方式以αc為臨界點分為不連續和連續兩種,但臨界點αc還取決于度分布的參數設置.另外,由于無標度網絡出現雙重相變情況時,網絡先以連續相變的形式滲流,所以將視為此時滲流相變點pc.通過比較圖8 和圖5,可以發現依賴組規模不均勻分布的網絡比依賴組規模均勻分布的網絡具有更強的魯棒性.

圖8 隨機網絡和無標度網絡在弱依賴組規模服從泊松分布時滲流相變點 pc 與α 的關系 (a) 〈M〉=3 的隨機網絡的滲流相變點 pc (或)與α 的關系,其中平均度 〈k〉 分別為4,5 和6;(b) 〈M〉=4 的隨機網絡的結果;(c)平均度 〈k〉 分別為4,5 和6 (度分布的冪指數 γ 分別為2.5,2.3 和2.1)且 〈M〉=3 的無標度網絡的結果;(d) 〈M〉=4 的無標度網絡的結果.圖中實線為一階滲流相變點,虛線為二階滲流相變點Fig.8.The percolation transition point pc as functions of α on random networks and scale-free networks when the interdependency groups size follows poisson distribution:(a) Results for random networks with the average interdependency group size〈M〉=3,where the average degree 〈k〉 is 4,5 and 6 from high to low;(b) the same results to panel (a) but for 〈M〉=4 ;(c)results for scale-free networks with the average interdependency group size 〈M〉=3,where the average degree 〈k〉 is 4,5 and 6 from high to low (corresponding to a power-law exponent of degree distribution 2.5,2.3 and 2.1,respectively);(d) the same results to panel (c) but for 〈M〉=4 .The solid line is the first-order percolation transition point ,and the dashed line is the second-order percolation transition point .

5 總結與展望

在一些真實的復雜系統中,網絡節點可能通過隱含的依賴關系而形成一些依賴組,其中一個節點失效后會對依賴組內其余節點造成一定程度的損害,進而會引發更多節點的失效而形成級聯過程.基于此,本文提出了一種具有“弱依賴組”的復雜網絡級聯失效模型,依賴組中節點的依賴方式由一種“節點對邊”的相互作用機制決定,與過去“節點到節點”的相互作用機制不同,當依賴組內一個節點失效時,組中其余節點都會受到一定程度的損害,而非完全失效.本文通過引入一個可調參數α來描述復雜網絡中弱依賴組內節點的依賴強度,并研究了網絡節點所形成的弱依賴組的規模,規模分布和依賴強度等幾個特征對于復雜網絡級聯失效動力學和網絡魯棒性的影響.

由于“節點對邊”的弱依賴機制的引入,本文發現網絡在級聯失效過程中存在兩種效應:組間級聯失效和組內級聯失效.具體而言,組間級聯失效表示一個節點的失效使依賴組外的部分節點不能通過失效節點連接到網絡的巨分支而失效,這些新增失效節點進而會造成更多節點的失效,組間級聯使得失效節點能夠跨依賴組傳播;組內級聯失效表示一個節點的失效會給依賴組內其余功能節點造成損害而失去部分連接,從而使這些節點脫離網絡巨分支而失效,這些新增失效節點進而給組內其余節點造成更大的損害而誘發更多節點失效,導致故障在依賴組內傳播,這一微觀效應在之前強依賴機制的模型中是不存在的,因在強依賴機制下,一旦依賴組中一個節點被刪除,其余節點將會被完全刪除.由于組外級聯失效的存在,某一個依賴組內產生的失效會在擴張到其他依賴組后又傳播到該依賴組內,從而進一步導致組內更多節點失效.而組內級聯失效的存在打破了網絡在部分節點在脫離網絡巨分支后的平衡.因此可以看出,二者存在協同作用.

在兩種級聯動力學的共同作用下,網絡以一階或二階相變的形式瓦解,且網絡瓦解的形式由節點之間的依賴強度決定.這說明依賴組內節點的依賴強度對網絡發生級聯失效的形式產生了至關重要的影響.當節點之間的依賴性較弱時,節點的失效不能對組內依賴節點造成較大的破壞性,從而抑制了故障的傳播,使系統通過二階滲流相變的形式發生破碎.當節點之間的依賴性較強時,節點的故障會以組內級聯的方式傳播到較為廣泛的范圍,從而導致系統的突然崩潰.這些結果表明,組內級聯失效過程影響著組間級聯失效的過程,并對網絡級聯失效的形式和網絡魯棒性起到了至關重要的作用.

數值模擬和理論分析的結果表明,隨著依賴組的規模和依賴組內節點的依賴強度的增大,網絡的魯棒性會逐漸下降,這是由于弱依賴組規模更小的網絡可將組內級聯限制在一個較小的范圍內,避免了失效在較大范圍內擴散.同時,依賴組規模不均勻分布的網絡比依賴組規模均勻分布的網絡具有更強的魯棒性,這是因為依賴組規模分布不均勻的網絡雖允許更大規模的依賴組出現,但大規模依賴組出現的概率較低,不容易受到攻擊,且攻擊數量較多且規模較小的依賴組也不會造成太大范圍的組內級聯,從而限制了組內級聯的范圍.

此外,在大多數情況下,當依賴組內節點依賴強度較弱時,隨機網絡魯棒性比無標度網絡差,而當依賴組內節點依賴強度較強時,無標度網絡魯棒性比隨機網絡差.這一結果表明,存在依賴組的情況下,度分布的異質性和依賴組規模分布的異質性都能夠對系統的魯棒性造成顯著的影響.

最后,本文還發現了無標度網絡中在依賴組中節點依賴強度適中時會發生二重相變的現象,這是由于無標度網絡度分布的異質性較強,當網絡受到一定程度的攻擊時所發生的級聯失效只能破壞為數眾多的度值較小的節點,而對于度值較大的節點還能形成穩定的簇結構,如將網絡徹底破壞還需更強的攻擊強度.

本文將“節點對邊”作用機理引入到了具有依賴組的的級聯失效模型中,描述了節點之間更為一般的依賴機制,不但對于理解依賴組的規模、規模分布和節點依賴強度等因素對網絡級聯失效的作用和級聯失效的發生機理具有重要的科學意義,而且對于通過依賴組的特征來對復雜網絡級聯失效的控制、預防干預策略的設計和魯棒性的優化具有重要的啟發意義.本文所研究的依賴組基于組內節點的相互依賴性完全相同的假設,然而在現實中依賴組內節點的相互影響可能不是完全等同的.因此后續的研究仍然存在較大的拓展空間,如依賴強度的非均勻性或非對等性對于網絡的級聯失效動力學是否具有顯著的影響？此外,依賴組內的節點是否能夠形成某種結構,依賴組的內節點的依賴結構是否對網絡級聯失效有較大的影響？這些問題都值得我們進一步進行實證或理論研究.