基于分步子空間映射的無標記膈肌運動預測算法

余 航 李晨陽 余紹德 馮冬竹 許錄平

呼吸運動(Respiratory motion)是放射治療(Radiation therapy,RT)中,導致誤差和不確定性的重要因素[1?2].一方面,現代放射治療技術可以達到毫米級的傳輸精度,如調強放療(Intensity-modulated radiation therapy,IMRT)[3];另一方面,呼吸運動可以導致胸部和腹部的腫瘤移動多達35 毫米[4].在此情況下[5],如果不對呼吸運動進行有效控制和補償,要么腫瘤得不到足夠的放射計量,要么腫瘤周圍的健康組織將會受到放射的傷害[6?7].因此,有效減少呼吸對器官和腫瘤運動的影響,對整個放射治療的進程和效果顯得尤為重要[8?10].

針對這一問題,研究者提出了多種不同的解決方法,包括:1)屏氣法[11?13];2)淺呼吸法[11?19];3)呼吸門控法[15?16];4)動態目標跟蹤法[17?21].呼吸門控法和動態目標跟蹤法都需要實時了解腫瘤的位置.呼吸門控法通過在呼吸周期的預定階段打開放射光束,從而減少正常組織的照射量.動態目標跟蹤法可以讓光束和腫瘤進行同步的運動,實現連續照射,是目前最為有效的呼吸管理技術.腫瘤的位置可以通過直接方式和間接方式來獲得.直接方式通過放射線成像系統對腫瘤或植入體內的標志物進行成像,該方法可以獲得人體內的結構信息,但會給患者帶來額外的輻射負擔[10,22?27],并且需要進行昂貴的、創傷性手術,因此目前還沒有廣泛應用.

間接方式是使用呼吸信息對內部解剖結構的運動進行建模和預測.Hoisak 等[27]通過肺活量測定和實時位置跟蹤系統,研究肺部腫瘤運動與呼吸運動的相關性.該方法的局限是,只使用了線性相關系數來度量腫瘤和參考物在一個方向上的運動相關情況.Paganelli 等[8]從核磁共振圖像(Magnetic resonance imaging,MRI)中提取SIFT (Scale-invariant feature transform)圖像特征,對基于圖像特征的跟蹤方法與基于標志物的跟蹤方法進行對比.該方法采用二次多項式進行建模,需要在人體表面放置標志物,并計算45個圖像特征的均值,較為繁瑣.文獻[9]通過實驗表明,相比于其它解剖結構,膈肌與呼吸運動具有更強的相關性.根據這一結論,很多研究者采用膈肌作為參考點,對腫瘤運動情況進行研究.文獻[28]針對不同患者,提出了一種基于膈肌的患者特異性呼吸模型,取得了良好的實驗結果.

另一方面,人體內部結構的運動情況,可以通過機體外部的觀察來進行預測.最近的研究[9]表明,人體整個外表面的運動與內部結構的運動具有很強的相關性.據此,文獻[29?30]使用K-means 算法對人體胸腹部表面的運動軌跡進行聚類,以產生呼吸運動的參考點.但是由于K-means 算法易受到初始值和數據結構的影響,該方法容易受到噪聲的干擾.Malinowski 等[1]將三個標記物固定在患者貼身背心上,據此來研究人體表面與腫瘤位置的相互運動關系.Ozhasoglu 等[4]通過使用光學監測裝置觀察附著在胸部和腹部的紅外發光二極管(LED),來研究呼吸運動對肺和胰腺腫瘤運動的影響.這兩種方法[1,4]均需在人體外表面放置標記物,因此較為繁瑣,易受到操作者的影響.

對體內膈肌和體外胸腹表面之間關系的準確、系統的研究,不僅可以提高呼吸運動管理的準確性,而且可以顯著降低放射治療的復雜性,但相關工作仍然較少,且要么需要患者佩戴標記物,較為繁瑣,要么模型建立比較簡單.考慮到這兩個器官具有不同的運動模式,其數據具有不同的分布結構,形成不同的子空間,無法直接進行準確的映射.針對這一問題,本文提出了一種新的分步子空間映射(Twostep subspace mapping,TSSM)算法,通過體外無標記胸腹部表面的測量來預測體內膈肌的運動情況.該方法無需患者佩戴標記物,且采用多種線性、非線性模型,系統地對體內膈肌和體外胸腹表面運動情況進行對比研究.本文首先針對4D CT 圖像,利用三維圖像分割方法,對體內膈肌和體外胸腹部表面的位移進行準確的測量.為了解決域自適應(Domain adaptation)問題,TSSM 首先利用主成分分析法(Principal component analysis,PCA)為每組數據構建特征子空間.然后通過線性嶺回歸(Ridge regression)優化過程,將膈肌數據與胸腹部表面數據連接起來,得到一個子空間映射模型.基于得到的映射模型,該方法可以通過體外胸腹部表面數據,對體內膈肌的運動情況進行預測.為了研究數據的非線性相關性,本文進一步將TSSM 擴展到基于核的分步子空間映射算法(Kernel TSSM,kTSSM),包括多項式核和高斯核.本文給出了兩種算法的解析解,其不需要遞歸迭代的操作,具有運算速度快的特點.對比實驗表明,這種分步映射的策略可以有效解決跨空間數據的預測問題,具有很好的準確性和魯棒性,優于經典的線性模型和ANN模型,本文也進一步給出了內部膈肌與外部胸腹部表面之間的運動關系模型.

本文的其余部分安排如下:第1 節具體介紹了所提方法和數據,實驗在第2 節中介紹,第3 節給出結論和討論.

1 方法

1.1 內部膈肌位移提取

當獲得患者的4D CT 圖像后,本文設計了一種三維圖像分割方法對其進行分割.在4D CT 圖像中,由于具有不同的組織結構,身體區域的體素值(Voxel)均大于800,而背景區域和肺部區域主要為空氣,其體素值在50 以下.考慮到圖像的背景、身體區域和肺部區域具有顯著的灰度差別,本文采用閾值法對其進行初步分割.具體地,本文設置閾值(本文設為500),首先將身體區域從背景中分割出來;然后根據區域面積,將圖像中的最大目標區域作為身體區域;最后進一步通過形態學方法,去除背景中的孤立區域并填充身體區域中的孔,從而得到身體區域的分割結果.在獲得身體區域之后,由于肺部區域在身體區域內部,并與身體區域的灰度值明顯不同,因此可以進一步執行閾值法分割出肺部區域,此時分割算法會將肺部區域作為目標,將身體區域作為背景.在最終的三維分割結果中,本文將背景體素設置為0,身體區域體素設置為1,肺部區域體素設置為3.圖1 顯示了第55、65 和75橫斷平面(Axial plane)的分割結果.圖2(a)顯示4D CT 第1 相位的三維分割結果,我們可以進一步地將肺部區域和身體區域分開,如圖2(b)、圖2(c)所示.

圖1 三維圖像分割結果橫斷平面展示圖,背景體素值為0,身體區域的體素值為1,肺部體素值為3Fig.1 3D segmentation images shown on the axial plane,where the background voxels is set to 0,the voxels of body area to 1,and the voxels of lungs to 3

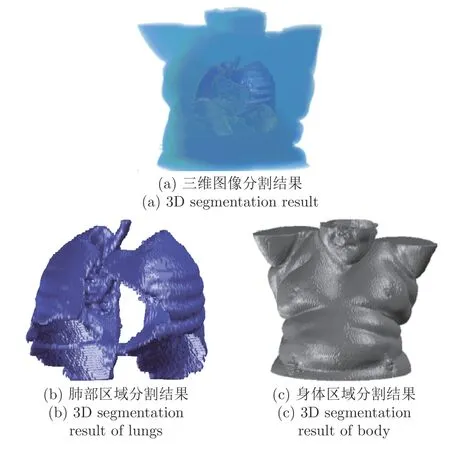
圖2 三維圖像分割結果,及其對應的肺部區域和身體區域Fig.2 A 3D segmentation result and the corresponding separated 3D lungs and body

膈肌位于肺部下面,并且與肺部的下邊界同步運動.考慮到難以直接通過4D CT 觀測到膈肌結構,因此本文使用肺部的下邊界來代表膈肌.本文工作面向的是肝癌立體定向體部放療(Stereotactic body radiation therapy,SBRT),其主要受到右肺的影響.因此,本文設計了右肺自動確定方法,來提取右肺區域,具體操作如下:首先,在肺部區域的三維分割結果上(如圖2(b)),從左到右分別計算各個矢狀平面(Sagittal axis)上肺部區域的面積(體素標簽為3 的數目),這樣以左右方向為橫軸,以肺部面積為縱軸,便可得到沿左右方向的肺部面積曲線,如圖3 所示.可以注意到,由于肺部的對稱性,在兩肺之間肺部面積值比較小,因此肺部面積曲線像字母 “M”一樣具有兩個峰,每個峰對應一個肺.因此,選擇肺部面積曲線兩個峰之間的最低點,便可以確定右肺所包含的切片.

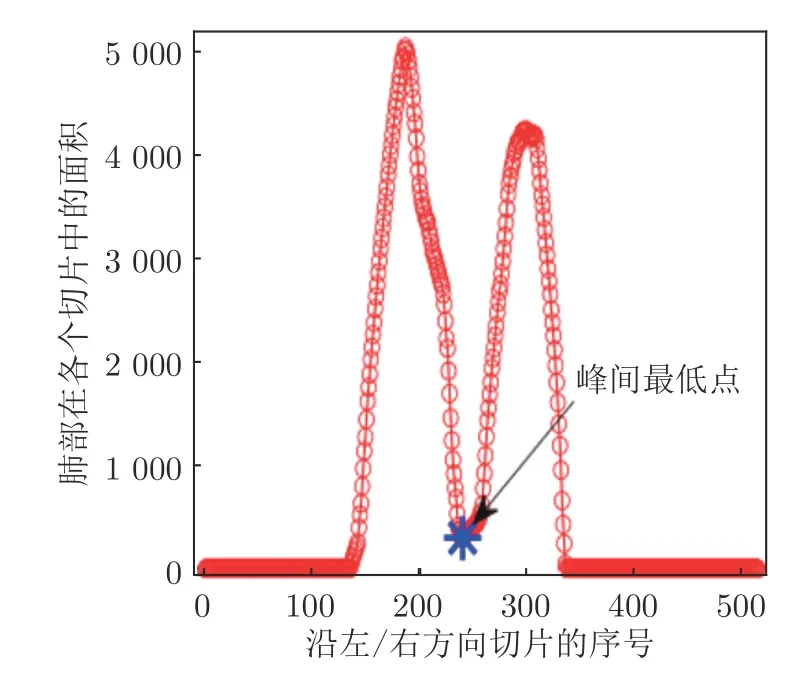
圖3 肺部面積沿左右方向的曲線Fig.3 The curve of lung area along the left/right direction

接下來,在右肺的三維分割圖像中,可以通過從下到上(解剖坐標系下)確定肺部區域的最低體素(在分割圖像中,身體體素值為1,肺部區域體素值等于3),從而獲得右肺下表面的三維圖像.在肺部下表面,有一些高于膈肌的體素,這些體素可以通過形態學運算進行去除.最后,可以獲得右肺下表面膈肌的三維空間坐標,表示為:

1.2 外部胸腹部表面位移提取

本節從三維分割結果的身體區域(如圖2(c)所示)中獲取胸腹部表面,進而計算胸腹部表面的位移.首先,沿前/后方向找出身體的邊界體素(體素值為1),獲得胸腹部表面.圖4(a)顯示了胸腹部表面在前/后方向的透視圖,其中像素灰度代表距最前端冠狀平面的距離.我們進一步對初始胸腹部表面進行處理,首先在得到的初始胸腹部表面圖上(如圖4(a)),沿左/右方向找到最寬的位置,該位置對應人體的肩膀,我們去除肩膀之上的區域.考慮到人體是一個類似的圓柱體,其在冠狀面的投影,將會包含正面的胸腹表面和人體兩側的區域,因此,為了更加準確地獲得胸腹部表面,本文運用腐蝕操作,來進一步地去掉人體兩側的區域.當人體進行呼吸時,人體兩側區域會沿左/右方向伸縮,其在冠狀面的投影有顯著的變化,且位于初始胸腹部表面的邊緣區域.因此,在對不同相位的初始胸腹部表面進行腐蝕后,得到的人體胸腹表面大小不一致,考慮到是同一個病人,為了統一大小,本文對所有相位的胸腹表面取交集,我們可以得到如圖4(b)所示的患者胸腹部掩膜.將該掩膜與初始胸腹部表面取交集,我們可以進一步獲得最終胸腹部表面,如圖4(c)所示,其表示為:

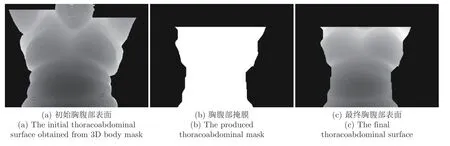
圖4 胸腹部表面Fig.4 The thoracoabdominal surface

相比于胸腹部的面積,胸腹部位移是非常小的,因此本文采用ICP 算法(Iterative closest point)[31]來計算胸腹部表面的位移.ICP 算法的輸出包括一個三維旋轉矩陣和一個平移向量.通過測試發現,人體胸腹部運動的旋轉角度小于0.5 度,其位移主要來源于平移,因此可以根據ICP 算法輸出的平移向量,來計算胸腹部表面的位移,表示為:

1.3 分步子空間映射

在提取胸腹表面的位移數據x ∈X和膈肌的位移數據y ∈Y之后,本節將要在它們之間建立映射F:X →Y,這樣對于任意新輸入測試數據,可以通過觀測胸腹表面的位移數據xTest,對膈肌的位移數據進行預測yTest=F(xTest).然而,胸腹表面和膈肌是兩種不同的解剖器官,其運動模式也不相同,所產生的兩種數據具有不同的分布結構.例如,在實驗中發現,有的病人膈肌位移很大,而其胸腹表面的運動卻很小.因此難以在這兩種數據集之間直接構造映射.為了解決這一問題,本節提出一種新的分布子空間映射算法(Two-step subspace mapping,TSSM).

本文將數據分為訓練數據和測試數據,x=xTrain∪xTest,y=yTrain∪yTest.假設器官結構相似的人,其胸腹部表面與膈肌有相似的運動情況.基于此假設,本文定義兩種距離:1)子空間域內距離:dintra(xi,xj)或dintra(yi,yj),i,j=1,2,···,N,計算在同一個子空間的兩個數據之間的距離;2)子空間域間距離dinter(xi,yj),i,j=1,2,···,N,計算來自不同子空間的兩個數據之間的距離.TSSM 算法的核心是找到一種映射,使同一患者數據的子空間域間距離dinter(xi,yi),i=1,2,···,N小于不同患者的子空間域間距離dinter(xi,yj),ij.子空間域內距離dintra能夠準確度量兩個器官運動的相異性.這樣對于新輸入的數據,我們通過對觀測數據xTest作映射來近似表示yTest.下面給出子空間的構造方法和映射方法.

膈肌位移數據和胸腹部表面位移數據的維數均為K維,因此可以生成K維子空間,選擇一組數據作為子空間的基,其他數據由這些基來表示,但這樣會導致數據冗余或不完整.為了克服這個問題,本文采用PCA 來構建子空間[32?34].PCA 通過最大均值差異最小(Maximum mean discrepancy,MMD)的準則,找到包含數據本質特征的公共子空間.

首先,對膈肌的位移數據和胸腹部表面的位移數據進行歸一化,表示為K維向量的形式,如下所示:

其中,λ ≥0 是控制收縮量的規則化參數.對式(6)關于β求導,并使等式等于0,則可以獲得最優表達式,如下所示:

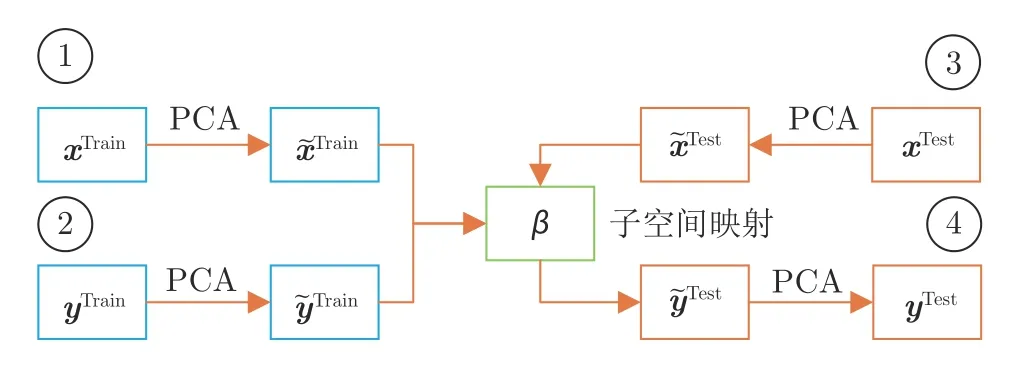
圖5 TSSM 算法的流程圖Fig.5 The flowchart of the propose TSSM

與支持向量機(Support vector machine,SVM)相似,僅使用線性模型進行子空間映射,無法充分地描述數據之間的關系.為了解決這個問題,本文進一步將TSSM 推廣到基于核的分步子空間映射算法(kTSSM).令?為非線性空間 Rx到高維空間 Zx的映射,核函數為K(xi,xj)=〈?(xi),?(xj)〉.可以注意到,預測數據可通過變換后數據?() 的線性組合來表示.因此,基于核函數的非線性嶺回歸優化變換可以表示為:

現有關于體內組織器官與體外基準點相對運動的研究[1?2,4,7?10],主要集中在線性模型或二次指數模型,為了更加詳細、全面地研究體內膈肌和體外胸腹表面的相對運動關系,以進行準確的膈肌位移預測,本文除了構造分步線性映射模型,并進一步將其擴展到了基于非線性核的映射模型.本文采用了兩種最常見的核函數:多項式核和高斯核,其中多項式核可以實現將低維的輸入空間映射到高維的特征空間,其并不只限于二次函數,通過升維操作可以提高建模的準確性,但多項式核的缺點是參數較多,容易出現過擬合現象.高斯核函數是最常用的核函數之一,可以將數據映射到無限維空間.考慮到本文醫用數據樣本較少,維數較高,且沒有數據分布的先驗知識,本文進一步選擇高斯核對體內膈肌和體外胸腹表面的相對運動關系進行度量.在實驗中,本文將對線性模型和兩種非線性模型進行對比研究,通過設置不同的參數,給出膈肌與胸腹部表面之間運動關系的準確度量.

2 實驗

2.1 患者情況與數據采集

本研究中使用的臨床數據由Philips Brilliance CT Big Bore Scanner 設備獲得,在這項研究中采用了來自20 位患者的4D CT 數據集,每個患者包括10個相位(具體為平均呼吸周期的0%,10%,···,90%).每個胸部CT 的大小為512×512×185個體素(Voxel),尺寸分別為1.1719 mm×1.1719 mm×3 mm (分別對應于A/P、I/S和L/R三個方向).在采集數據時,病人按正常狀態、有規律的呼吸.

在實驗中,我們選擇相關研究中的經典線性模型和非線性模型,與本文所提三種模型進行對比,具體如下:OLS (Ordinary least squares)多變量線性回歸模型[1]、人工神經網絡模型(Artificial neural network,ANN)、TSSM、多項式核的kTSSM 和高斯核的kTSSM.本文采用三個指標,對5 種算法的性能進行定量評估:均方誤差(Mean-square error,MSE)、R2誤差和平均絕對百分比誤差(Mean absolute percentage error,MAPE),計算方法如下:

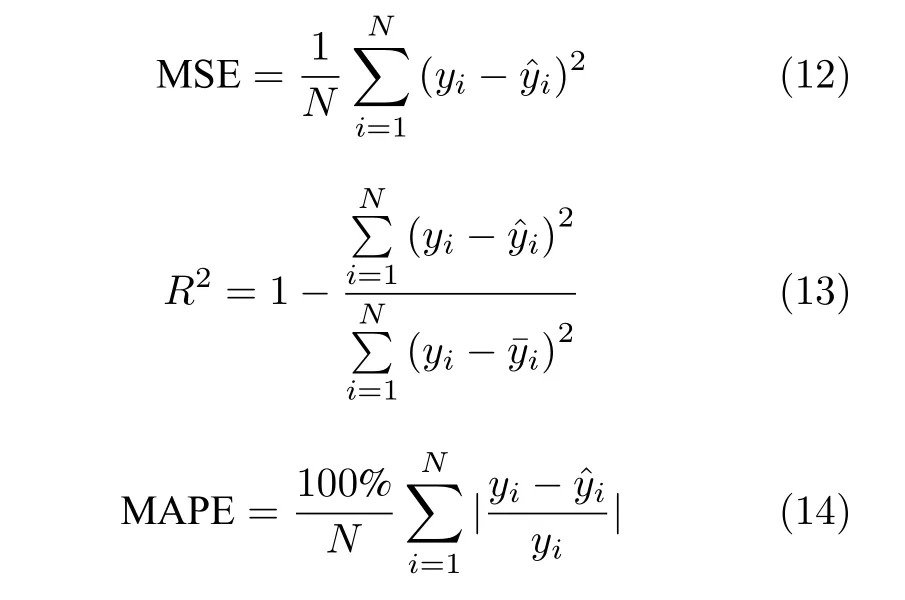
其中,yi是模型的實際值,是模型實際值的均值,是模型的預測值.MSE 衡量模型的預測均方誤差,MSE 的值越低,預測結果越好.R2比較模型的優劣性,消除數據分布域對實驗結果的影響.R2的范圍為(?∞,1],值越大預測效果越好.MAPE 衡量模型的預測值與實際值的平均偏差,消除數據取值范圍的影響,值越低預測結果越好.

在實驗中,本文采用K-fold 策略將整個數據集分為訓練數據和測試數據,其中80%的隨機樣本作為訓練數據,其余樣本進行模型測試.為了評估該算法的魯棒性,在訓練數據和測試數據中分別添加高斯噪聲σ={0.1,0.2,0.3,0.4,0.5},從而分析不同級別的高斯噪聲對算法的影響.本文算法參數選擇如下:對于嶺回歸優化,λ={10?10,10?9,···,1010};在高斯核K(x,y)=中,σkernel的值等于{0.1,0.2,0.4,0.8,1.6,3.2,6.4,12.8};在多項式核K(x,y)=(xTy+c)d中,d={0.5,1,···,11},c={?10,?9,···,10};對于ANN,本文采用兩層前饋神經網絡,其隱層節點數依次選擇{2,3,4,···,29,30}.對于每個算法的每組參數,本文單獨運行算法100 次,選擇每個算法的最優參數組合,并獲得統計結果.所有算法的運行環境相同,均為Inter Xeon 3.6 GHz,32 GB 內存,Windows10 和MATLAB R2019b 平臺.

2.2 膈肌和胸腹部表面的位移

圖6 膈肌和胸腹部表面的位移,每一種顏色的曲線對應一個患者的數據Fig.6 The displacement of diaphragm and thoracoabdominal surface,where each color corresponds to a specific patient＇s data

由于性別、年齡、體型和情緒等都會對身體器官的運動產生影響,不同患者器官運動的幅度不盡相同.因此,根據式(5)對膈肌和胸腹部表面的位移進行歸一化,結果如圖7 所示.從圖7 可以看出,不同患者胸腹部表面在前/后方向,膈肌在下/上運動方向的數據分布更加一致.

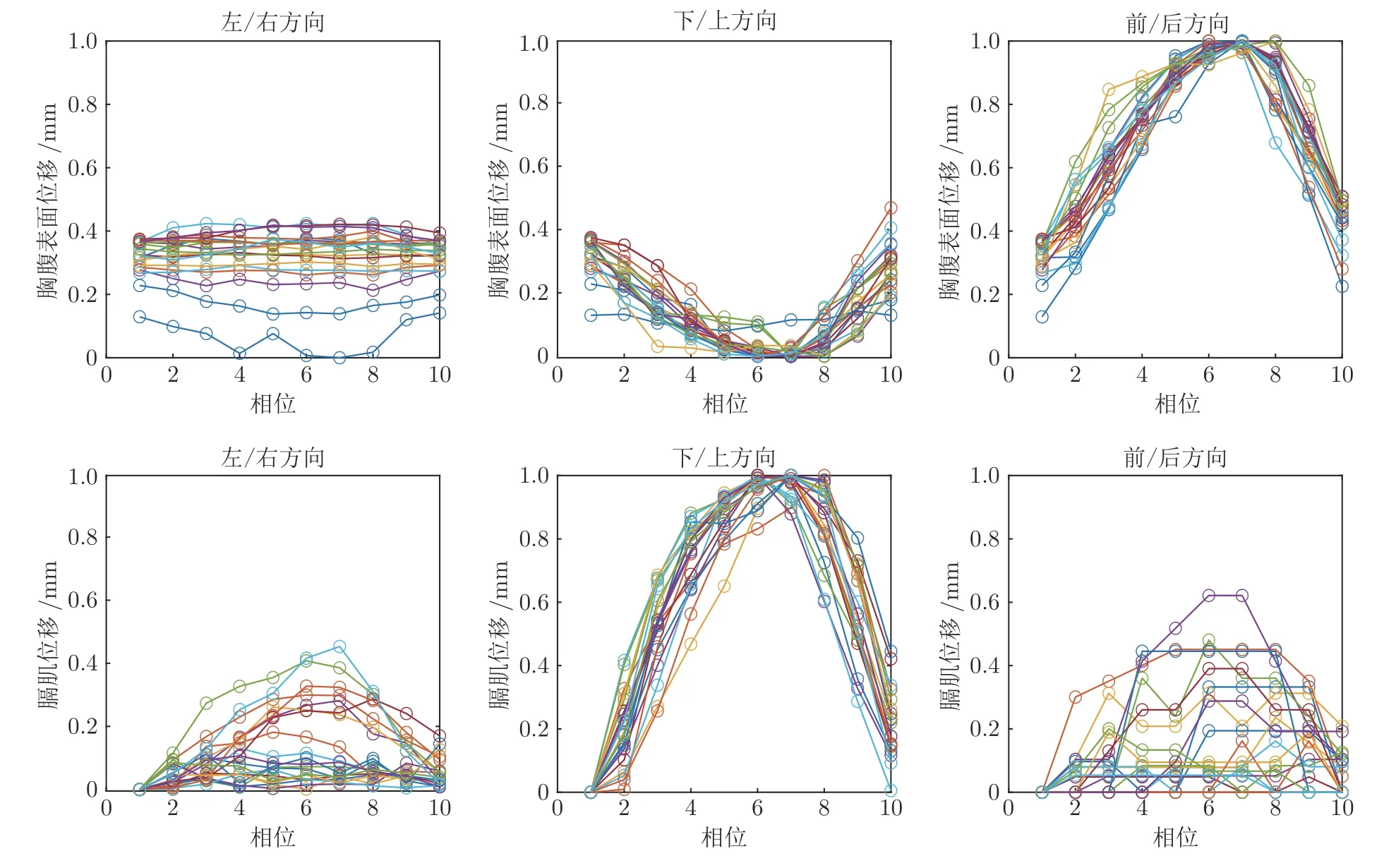
圖7 歸一化后的膈肌和胸腹部表面的位移,每一種顏色的曲線對應一個患者的數據Fig.7 The displacement of diaphragm and thoracoabdominal surface after normalization,where each color corresponds to a specific patient＇s data

2.3 三個方向的預測

在本節中,將根據胸腹部表面在三個方向的運動,來預測膈肌在三個方向上的運動.本文將同一患者三個方向10個相位的數據連接在一起,形成一個包含30個元素的向量,胸腹部表面位移向量為輸入,膈肌位移向量為輸出,預測結果如表1 所示.其中每個單元有兩個數據,前一個值代表100 次獨立運行的平均值,括號中的值代表100 次獨立運行的標準偏差.本實驗記錄MSE 和MAPE 的最小值,記錄R2的最大值,加粗標記代表5 種算法中的最佳結果.在表1 中,從上到下,噪聲等級依次增加.從表1 可以看出,同為線性模型,TSSM 算法優于OLS 模型;非線性模型ANN 的表現較OLS 模型要更好.所提的三個算法的預測結果相近,MSE值和R2值均令人滿意,但多項式核的kTSSM 算法獲得多數的最佳預測值.值得一提的是,由于向量取值的不平衡性,兩種組織器官在有的相位和方向上移動范圍大,在其它相位和方向上移動范圍小,取值范圍小的預測值會增加MAPE 值,因此使得MAPE 值均超過100%.

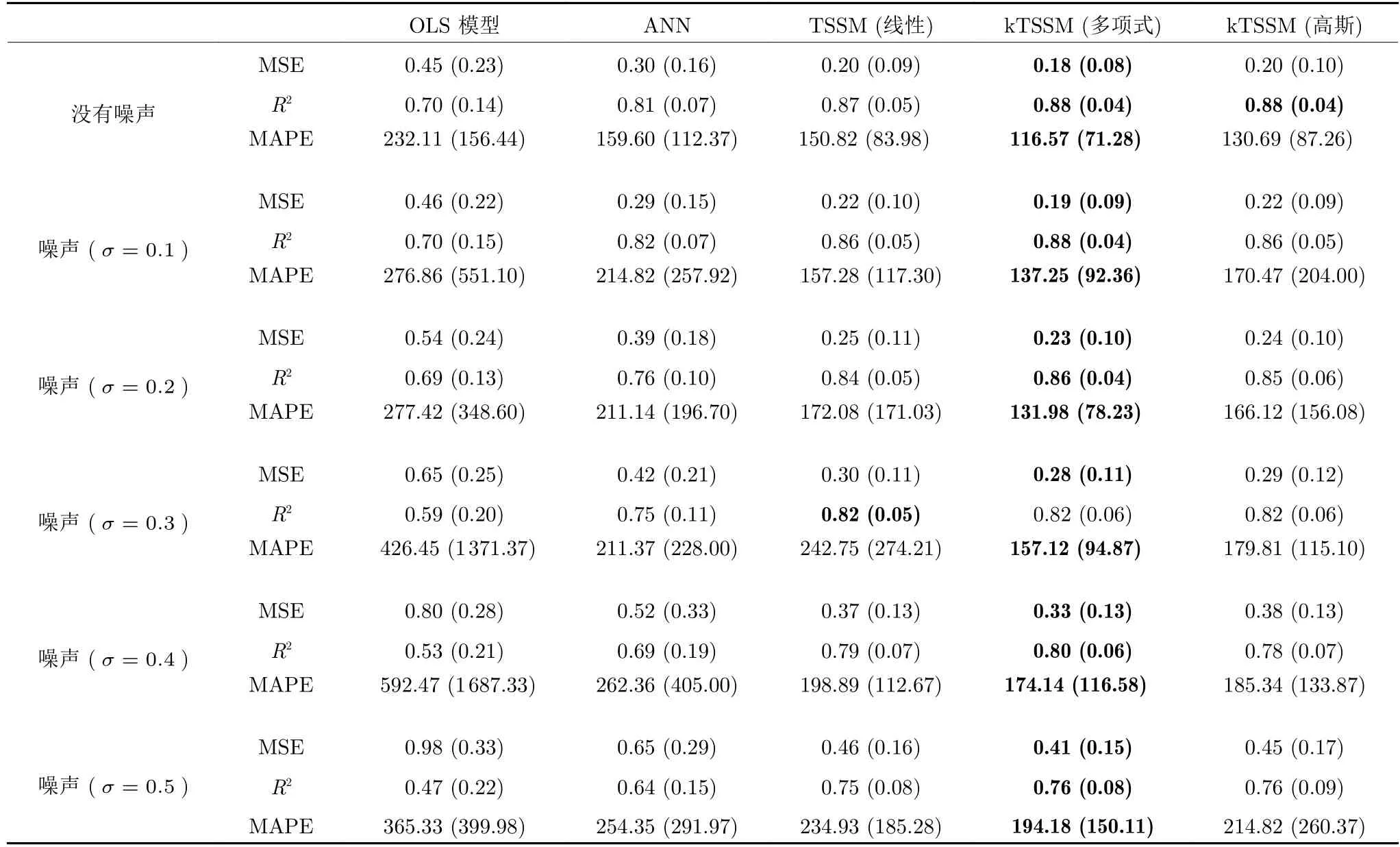
表1 在三個方向上的預測結果Table 1 Prediction results in three directions

圖8 顯示5 種算法預測結果,其對應100 次獨立運行中,MSE 的中間值對應的結果.圖8(a)為 OLS模型,圖8(b)為ANN,圖8(c)為TSSM,圖8(d)為多項式內核的kTSSM,圖8(e) 為高斯內核的kTSSM.在每個子圖中,有4個預測結果(占總數的20%),其中橫軸表示10個相位,縱軸表示實際位移值,紅色曲線表示實際值,藍色曲線表示預測值.在橫軸上,L/R表示左/右方向,I/S表示下/上方向,而A/P表示前/后方向.從圖8(a)可以看出,OLS 模型在下/上方向上可以預測膈肌運動,但是在某些相位,OLS 模型在左/右和前/后兩個方向上的預測效果不佳,仍然存在誤差.同為線性模型,TSSM 算法具有更好的預測效果.與OLS 模型相比,非線性模型ANN 的表現更好,而本文設計的kTSSM (多項式)在大多數情況下,取得了最佳的預測結果.

圖8 三個方向的預測結果.該結果對應于100 次運行MSE 的中位數值Fig.8 Prediction results corresponding the median MSE value in three directions after 100 independent runs

圖9 顯示了100 次獨立運行的統計箱圖,其中橫軸表示三個方向10個相位,縱軸表示預測值和實際值之間的絕對誤差.圖9 子圖中的每個方框都包含100 次獨立運行的結果,在每個方框上,中心的標記表示中值,而框的底部和頂部邊緣分別表示第25個和第75個百分點,“+”符號代表異常值.從圖9我們可以清楚地看到,圖9(a)中縱軸的范圍比其他子圖中的大得多,圖9(b)中縱軸取值范圍居中,而圖9(c)～圖9(e)的誤差絕對值比較小,這也說明本文所提的方法具有更優、更穩定的預測性能.從圖9(c)～圖9(e)可以看到,下/上方向上的統計值低于其他方向上的統計值;對于下/上方向,位于中間相位(5、6、7 相位)的預測誤差較小,這表明當患者處于滿吸氣狀態時,預測效果會更好.

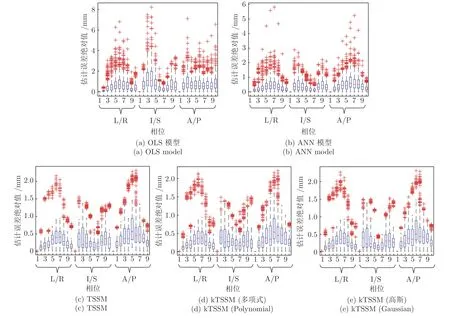
圖9 三個方向各相位預測誤差的統計箱圖Fig.9 Boxplot of the prediction performance on every phase in three directions

2.4 主方向的預測

在本節中,僅使用胸腹部表面的前/后方向,對膈肌的下/上方向的運動進行預測.表2 顯示了100 次獨立運行后的預測結果.圖10 顯示5 種方法對應MSE 中間值的預測結果.圖11 為每個相位的預測誤差絕對值的統計箱圖.從表2 可以看出,TSSM 算法的性能優于OLS 模型.ANN 算法結果優于OLS 模型.在沒有左/右和前/后方向的數據影響的情況下,TSSM 算法的性能得到了很大的提高,而且MAPE 值已降至100%以下,證明了TSSM算法的良好性能.從圖10 可以看出,本文所提方法均取得了令人滿意的預測結果.圖11 可以看出,在第5、6、7 相位上的預測結果,要好于在其它相位上的預測結果,這也進一步證明,當患者處于滿吸氣狀態時,從外部體表能更加準確地預測體內結構的運動.

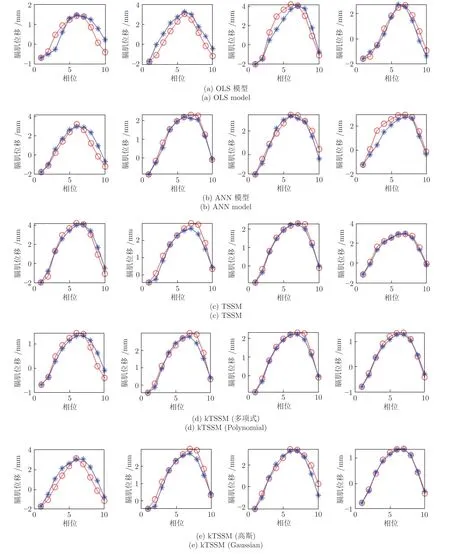
圖10 主方向的預測結果,該結果對應于100 次運行MSE 的中位數值Fig.10 Prediction results corresponding the median MSE values in the principal direction after 100 independent runs

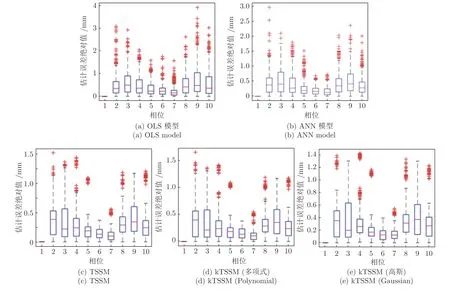
圖11 主方向各相位預測誤差的統計箱圖Fig.11 Boxplot of the prediction performance on every phase in the principal direction

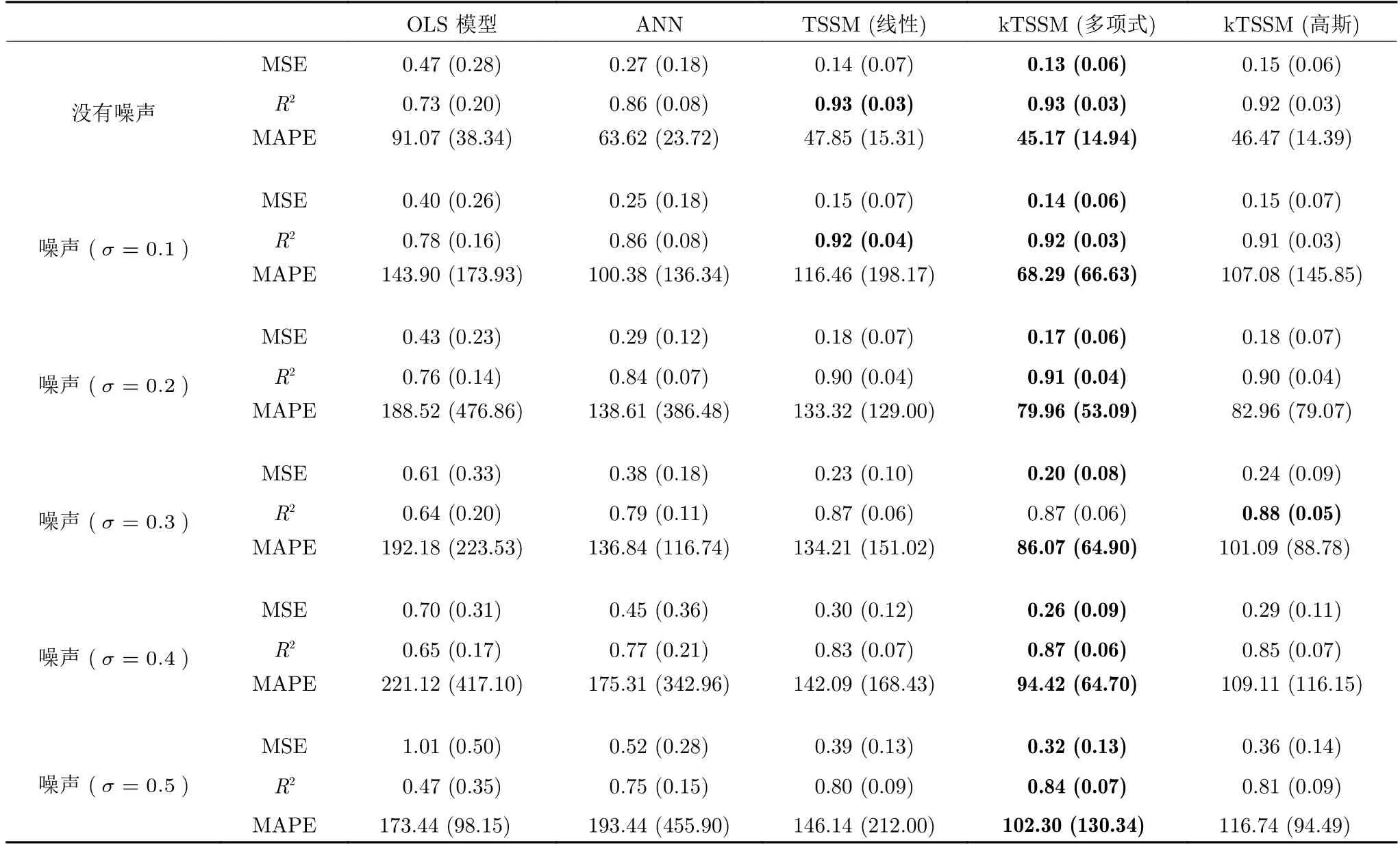
表2 在主方向上的預測結果Table 2 Prediction results in principal direction

2.5 噪聲的影響

本節驗證算法的魯棒性.噪聲對三個方向預測性能的影響如圖12 所示.在圖12 的子圖中,橫軸表示高斯噪聲的等級,縱軸表示算法100 次獨立運行后指標的平均值.圖13 是噪聲對主方向預測的影響,可以看出,隨著噪聲等級的增加5 種算法的性能都會下降.但是與OLS 模型相比,ANN 算法和TSSM 算法的下降速度較慢且穩定,這表明ANN,TSSM 和kTSSM 算法比OLS 模型對噪聲的魯棒性更高;對于準確性和穩定性,尤其是在MAPE度量方面,具有多項式核的kTSSM 算法在5 種算法中表現最好.

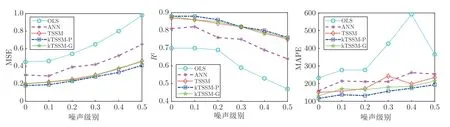
圖12 噪聲對三個方向預測性能的影響Fig.12 Influence of noise on the prediction in three directions

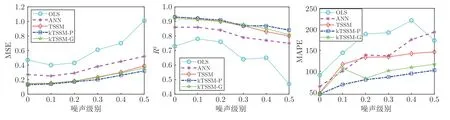
圖13 噪聲對主方向預測性能的影響Fig.13 Influence of noise on the prediction in principal direction

2.6 關于算法參數的討論

TSSM 和kTSSM 取得最優值時,參數設置如表3 所示.對于線性模型TSSM,其參數只有嶺回歸一個參數λ,其取值范圍為λ={10?10,10?9,···,1010}.在絕大多數情況下,λ的最優設置為1,只有兩次為0.1,這兩次對應λ=1 的預測結果與最優結果接近.因此,TSSM 對膈肌位移的預測是比較穩定的,受參數影響較小,可直接設置為1 即可.對于kTSSM(高斯)模型,其參數為λ和σkernel,其中λ的取值范圍與TSSM 相同,σkernel={0.1,0.2,0.4,0.8,1.6,3.2,6.4,12.8}. 可以看到,在絕大多數情況下λ=0.1,σkernel=0.1 或0.2,只相差一個取值間隔.在實驗結果中我們發現,當σkernel=0.1 或σkernel=0.2 時,kTSSM (高斯)模型的預測結果非常相近,具有很好的穩定性.kTSSM (高斯)模型的參數設置,可按如下策略:當獲得的數據沒有噪聲或者比較干凈時,可直接設置為λ=0.1,σkernel=0.2;當數據噪聲比較 大 時,參 數 可 直 接 設 置 為λ=0.1,σkernel=0.1.對于kTSSM (多項式)模型,其具有三個參數λ、d和c,其中λ的取值范圍與TSSM 相同,d={0.5,1,···,11},c={?10,?9,···,10}.可以看到,相比于TSSM 和kTSSM (高斯)模型,kTSSM (多項式)模型的參數變化浮動較大,特別是同時進行膈肌三個位移方向的預測時,嶺回歸參數λ、指數d隨著噪聲的增加逐漸降低,最后維持在λ=10 和d=1.這主要是因為在沒有噪聲或噪聲較小時,kTSSM(多項式)模型發生了過擬合現象;當噪聲增加時,降低了kTSSM (多項式)模型對數據的敏感性,因而最優參數可以達到相對穩定.kTSSM (多項式)模型對于主方向的預測,受參數影響較小,比較穩定,λ在1 上下浮動,d在0.5 和1 之間選擇,參數c設置為4 即可.從kTSSM (多項式)模型的參數d可以看出,胸腹部表面與膈肌的相對位移,近似滿足線性模型(d=1),這一點也可以通過TSSM 的參數穩定性得到驗證.盡管kTSSM (多項式)模型在實驗中取得了最好的預測結果,但是考慮到kTSSM(多項式)模型具有更多的參數需要設置,并容易出現過擬合現象,本文認為在實際中,只需要采用線性模型TSSM 即可達到準確的預測結果.

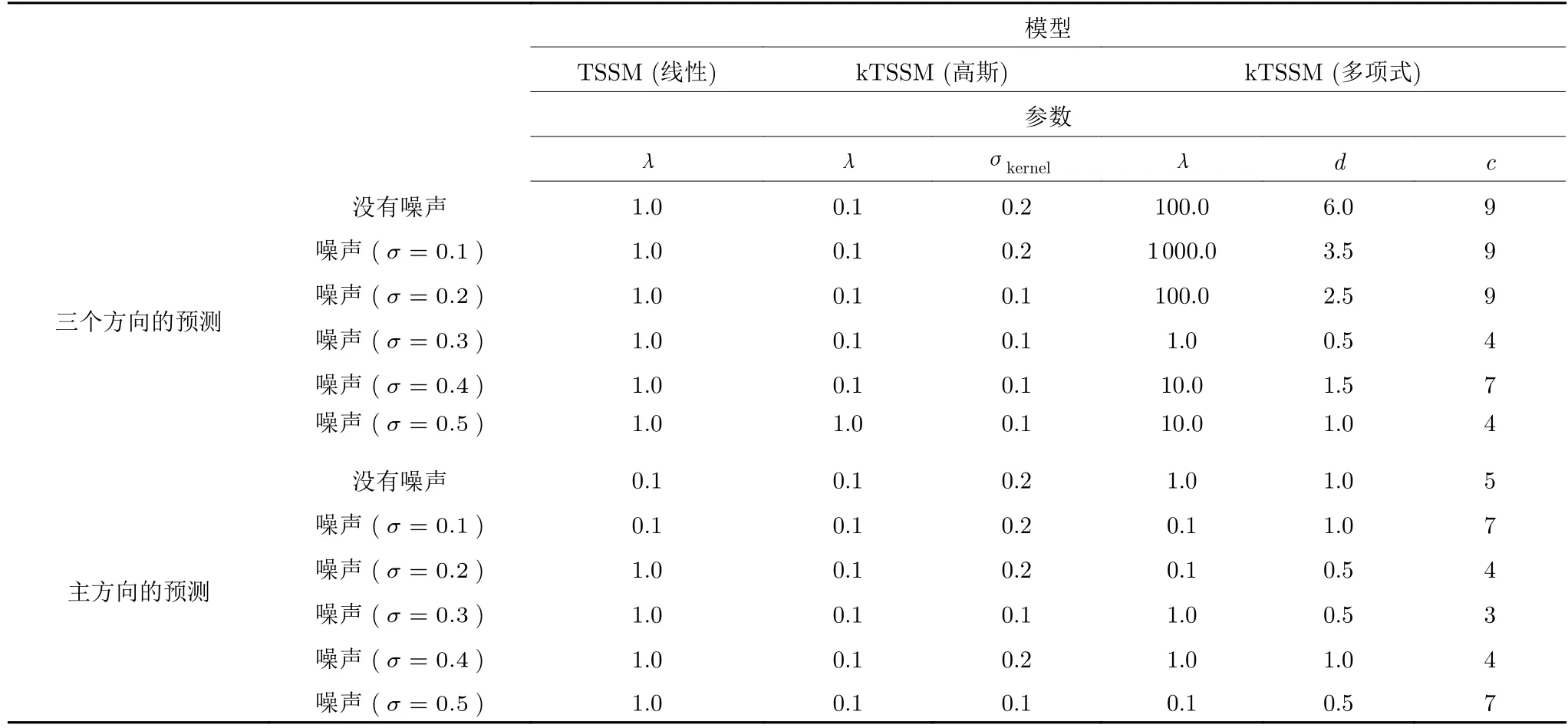
表3 TSSM 和kTSSM 取得最優預測結果時的參數設置Table 3 Parameter setting of TSSM and kTSSM for optimal results

本文進一步使用TSSM 模型研究PCA 算法中不同的閾值ε對算法性能的影響.我們選擇不同的閾值ε={1,10?1,10?2,10?3,10?4,10?5,10?6},確保由PCA 構造子空間的維數,從1 維逐漸變到原始數據的維數,然后在不同的噪聲水平(σ={0.1,0.2,0.3,0.4,0.5}) 下,單獨運行TSSM 模型(λ=1) 100 次.計算結果如圖14 所示,其中圖14(a)為三個方向預測的統計結果,圖14(b)為主方向預測的統計結果.每個子圖中,橫坐標表示不同的閾值ε,縱坐標依次為子空間維數、MSE 值、R2值和MAPE值.可以看到,當ε=1 時,此時PCA 構造的子空間只有1 維;隨著ε的增大,子空間維數逐漸增大至原始數據的維數,即PCA 沒有對原始數據進行降維.隨著ε的增大,MSE 值逐漸減小,這主要是由于子空間映射時,維數越多,信息量損失越小,因此可以得到更加準確的預測結果.同時注意到,MSE值、R2值和MAPE值的變化范圍非常小,特別是R2值和MAPE 值僅出現小范圍的變化,可近似看作穩定.即使當PCA構造的子空間只有1 維時,TSSM模型也能取得令人滿意的預測結果,這也說明PCA構造的子空間能夠有效提取原始數據的主要成分,具有很強的穩定性.為了對比驗證所提算法的有效性,本文在實驗中選擇ε=10?4,此時PCA 構造的子空間保留了原始數據絕大部分信息,信息損失量較少,獲得預測 結果較為準確.

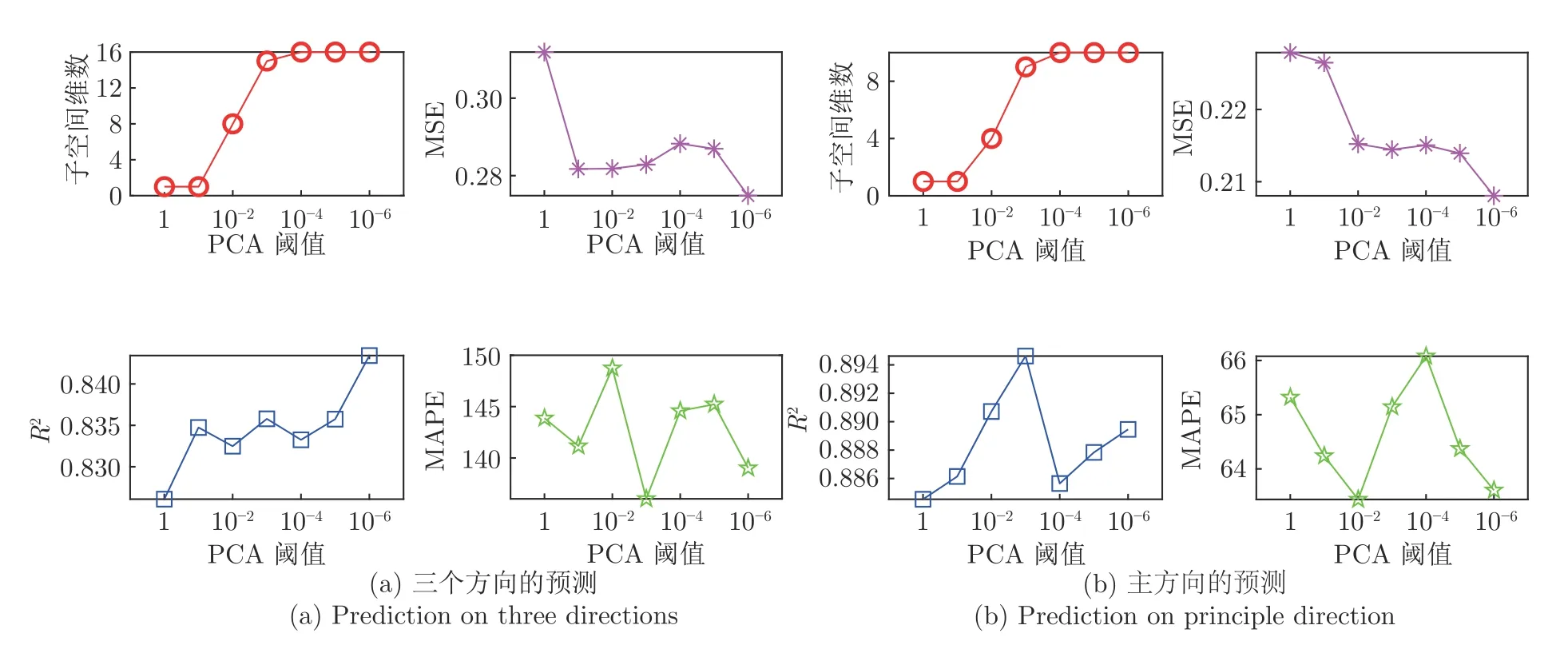
圖14 PCA 中的閾值 ε 對TSSM 預測模型的影響Fig.14 The influence of ε in PCA on the prediction performance of TSSM

3 討論和結論

呼吸運動是放射治療(RT)中導致誤差和不確定性的重要因素[1?2].本文首先采用三維圖像分割技術,對4D CT 圖像進行分割,在不使用標記物的情況下,通過提取膈肌的質心以準確度量膈肌的位移,使用ICP 算法計算胸腹部表面的位移.為了解決跨空間預測問題,本文提出了一種新的分步子空間映射算法(TSSM),通過構造特征子空間,并在高維子空間中進行映射,從而可以有效地提高跨空間數據預測的準確性.

對20 位患者真實數據的實驗表明,本文提出的方法可以有效地描述膈肌和胸腹部表面的運動情況.相比于通過原始空間的直接預測,TSSM 算法在準確性和魯棒性方面均優于經典線性的OLS 模型和非線性的ANN 模型.考慮到具有多項式核的kTSSM 算法比TSSM 算法具有更多的參數,容易出現過擬合現象,因此在實際應用中,我們建議直接應用TSSM 算法,線性模型已經可以獲得令人滿意的預測效果.值得一提的是,我們發現在病人吸氣處于最高點的位置時,預測效果會更好.所提算法具有解析解,總計算時間(訓練加上測試)在0.6 ms以下,可以達到實時處理速度,運行效率較高,這將有助于提高放射治療中門控技術和跟蹤技術的效率和精度.