借問考生錯何處，題意暗指素養(yǎng)故

周穎穎

摘要：本文通過錯例示范法，研究立體圖形中的最短路徑問題，分析學生產生錯誤的本質原因，從而啟發(fā)教師在平時教學過程中，從五個方面重視學生數(shù)學學科素養(yǎng)的培養(yǎng).

關鍵詞：錯例示范;最短路徑;數(shù)學素養(yǎng);

原題呈現(xiàn)與試題分析

【原題呈現(xiàn)】

在幾何體表面上，螞蟻怎樣爬行路徑最短？

如圖①，圓錐的母線長為12cm，B為母線OC的中點，點A在底面圓周上，的長為4πcm，在圖②所示的圓錐的側面展開圖畫出螞蟻從點A爬行到點B的最短路徑，并標出它的長（結果保留根號）.

圖③中的幾何體由底面半徑相同的圓錐和圓柱組成，O是圓錐的頂點，點A在圓柱的底面圓周上. 設圓錐的母線長為l，圓柱的高為h.

①螞蟻從點A爬行到點O的最短路徑的長為_______（用含h，l的代數(shù)式表示）.

②設的長為a，點B在母線OC上，OB=b，圓柱的側面展開圖如圖④所示，在圖中畫出螞蟻從點A爬行到點B的最短路徑的示意圖，并寫出求最短路徑的長的思路.

【試題分析】

本題是立體圖形表面爬行的最短路徑問題，需要學生將立體圖形轉化成平面圖形，第一問也正是為這一點做好鋪墊：將立體圖形展開成平面圖形，繼而在平面圖形上找到最短路徑. 第二問是在組合的立體圖形表面找最短路徑，難點是將立體圖形展開成平面圖形，這里需要學生具有類比聯(lián)想的能力：圓錐的平面展開圖是一個扇形和一個圓，它們通過一個點連接，從而可以類比出本題的組合圖形的平面展開圖.而且還考察了學生的臨界思想：展開后找最短路徑轉化成兩條線段的和的最小值，當三點共線時最小.本題對學生的綜合能力要求高，考察了學生的轉化思想、化歸思想以及臨界思想.

二、解法與思路分析

解（1）如圖①，AB即為最短路徑.

（2）①h+l

②如圖②，AB即為最短路徑.

求最短路徑的長的思路如下：

設切點為E，作AF⊥EC，連接OE，作BG⊥OE.

第一步，設EF=x，則=EC=a-x，于是∠EOC=? ? ? ? ? ? ? .

第二步，解Rt?OBG可得BG=b·cos∠EOC ，OG=b·sin∠EOC ，

于是EG=l-b·cos∠EOC

第三步，由ΔAEF∽ΔEBG得，可求出x的值.

第四步，根據(jù)勾股定理求出AE和BE，則最短路徑的長為AB=AE+BE.

特別地，若點B在O或者C處，易得最短路徑長.

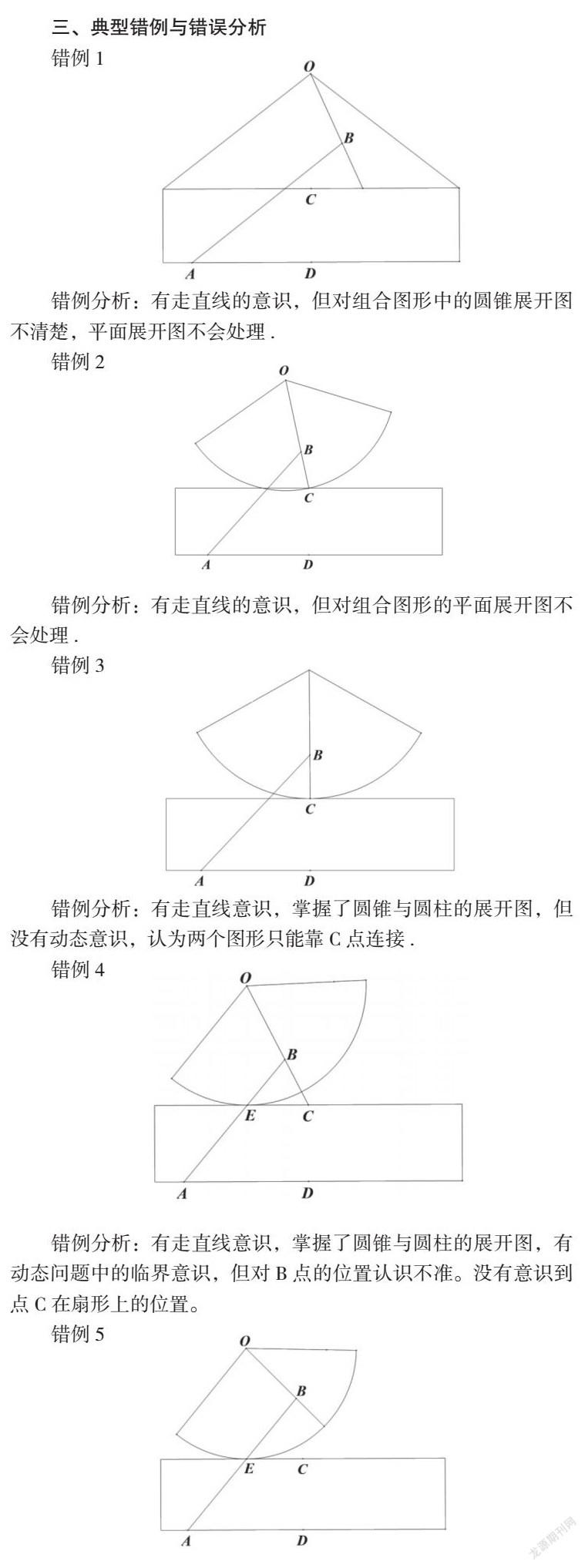
三、典型錯例與錯誤分析

錯例分析：有走直線的意識，但對組合圖形中的圓錐展開圖不清楚，平面展開圖不會處理.

錯例分析：有走直線的意識，但對組合圖形的平面展開圖不會處理.

錯例分析：有走直線意識，掌握了圓錐與圓柱的展開圖，但沒有動態(tài)意識，認為兩個圖形只能靠C點連接.

錯例分析：有走直線意識，掌握了圓錐與圓柱的展開圖，有動態(tài)問題中的臨界意識，但對B點的位置認識不準。沒有意識到點C在扇形上的位置。

錯誤分析：有走直線意識，掌握了圓錐與圓柱的展開圖，有動態(tài)問題中的臨界意識，沒有意識到點C在扇形上與點E構成的弧長等于EC.

四、教學啟示

（一）在幾何教學中，培養(yǎng)學生“降維式”思維方式

初中生更擅長解決平面幾何問題，該題的難點是給出的圖形是由圓柱與圓錐組成的立體幾何問題.如何把螞蟻從點A爬行到點B的最短路徑的立體幾何問題，轉化為平面幾何問題，是一大難點.大多數(shù)學生均能想到將立體幾何展開，可這道題與以往的立體幾何平面展開圖不同：圓柱和圓錐的展開圖如何合成一個圖.這需要借鑒立體圖形的平面展開圖獲得的經驗產生聯(lián)想.

（二）經歷由“靜”到“動”的思維過程，培養(yǎng)學生化歸與轉化的數(shù)學思想

在幾何問題中，很多看似靜態(tài)的問題，在嘗試、分析、挖掘題目后其實本質是一個動態(tài)問題.如本題：圓錐的展開圖扇形與圓柱的展開圖矩形是通過一個點來連接的，這個點是任意的，這就相當于可以將扇形在矩形上滾動，是一個動態(tài)問題，在這個動態(tài)問題中找出最值.在平時的教學中，碰到此類問題，要鼓勵學生去挖掘、去分析、去化歸，以獲取這類經驗.

（三）利用最近發(fā)展域，培養(yǎng)學生類比猜想能力

兩點之間線段最短，學生對這個結論是比較熟悉的。本題問的是螞蟻從點A爬行到點B的最短路徑，學生根據(jù)經驗，猜想：線段最短，進而會去尋求何時為線段，從而想到使得點A，E，B在一條直線上時.至于猜想正確與否，題目中并沒有要求證明，因為要用到高中的導數(shù)知識.“猜想——驗證”是數(shù)學學習的重要方法，有時候猜想比驗證更重要，如果在平時的教學過程中，有意識地利用學生已有的知識，引導其進行類比猜想，那初中生的猜想能力以及創(chuàng)新能力均能得到有效地發(fā)展，為后期的學習打下堅實的基礎.

（四）強化臨界意識，培養(yǎng)學生特殊與一般的數(shù)學思想

在教學中，學生面對一些“動態(tài)型”的應用問題常常會束手無策.如果能想象問題的動態(tài)情景，尋找臨界條件，問題就能迎刃而解.比如本文中研究的這道題，求螞蟻從點A爬行到點B的最短路徑，就是一個動態(tài)問題.最終把其轉化為：當點A，E，B在一條直線上時最短，此時點E的位置就是一個臨界點.在教學的過程中，鼓勵學生由一些特殊的情況進行大膽的猜想，再嘗試用嚴格的數(shù)學方法進而論證一般情況，培養(yǎng)學生特殊與一般的數(shù)學思想，進而培養(yǎng)學生敢于質疑，勇于創(chuàng)新的科學品質.

（五）在日常教學與解題教學中，注重分析的過程，有大局觀

平時解題過程中，學生傾向于想到一步，就求解一步，以“量”的形式解題，缺乏對題目的定性認識：這可求嗎？為什么可求？要想提高學生的定性認識，我們在平時的教學中要有意識地去讓學生定性的分析求解的過程，有哪些條件可求什么，進而可求什么，這樣的分析方式;在代數(shù)教學時滲透各個公式中有幾個未知量，知道其中幾個量其余幾個量就可求的思想;在幾何教學中滲透“確定即可求”的思想：如三角形的兩邊及其夾角確定，三角形也隨之確定，進而三角形的其他基本元素也是確定的，可求解的等等.