一類分數階p-q型臨界橢圓邊值問題的非平凡解

張愛旎， 鄧志穎

重慶郵電大學 理學院，重慶 400065

本文討論含有Sobolev臨界指數項的分數階p-q型橢圓系統

(1)

形如方程組(1)的分數階橢圓邊值問題具有很強的物理背景和廣闊的應用前景，廣泛應用于諸多領域，例如反常擴散問題、極小曲面問題、最優化問題、相變問題等[1-2]．

近年來，p-q型臨界橢圓邊值問題受到了學者們的廣泛關注．例如文獻[3]討論了p-q型橢圓耦合系統

(2)

其中Ω?RN是包含原點的有界光滑區域，10，α，β>1滿足α+β=p*，p*是Sobolev臨界指數．應用山路引理和Lusternik-Schnirelmann(簡稱LS)疇數理論，得到了在一定條件下問題(2)至少存在cat(Ω)個正解．有關帶有臨界指數項的結論還可參見文獻[4-10]．

近年來，分數階臨界橢圓邊值問題引起了人們的廣泛興趣，目前已獲得了一定的研究成果[11-17]．例如文獻[14]研究了分數階p-q型橢圓耦合系統

(3)

研究方程組(1)的主要困難在于：一方面，方程組(1)含有Sobolev臨界指數項，使得對應的能量泛函失去緊性；另一方面，p-q型方程沒有p-Laplace方程的齊次性，從而通常的變分方法和分析技巧受到很大的限制．本文應用山路引理克服了上述困難．

設a(x)，b(x)，H滿足下述條件：

(H2)H(-ζ，-τ)=H(ζ，τ)，?(ζ，τ)∈R2；

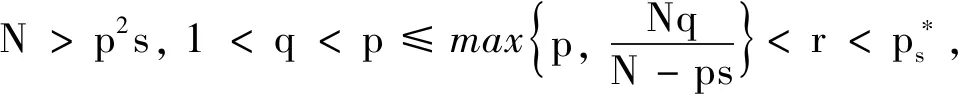
全文中，設Ω?RN為有界光滑區域，s∈(0，1)，p>1，C，C1均代表正常數．用Xs，p(Ω)表示通常的分數階Sobolev空間，

其范數定義為

設乘積空間

這兩個Banach空間的范數分別定義為

令空間E=Wp∩Wq，賦以范數

‖(u，v)‖E=‖(u，v)‖s，p+‖(u，v)‖s，q

下面我們定義分數階Sobolev最佳臨界常數

(4)

(5)

證該證明與文獻[18]中引理3.2的證明類似．

(6)

容易驗證J(u，v)∈C1(E，R)，從而泛函J(u，v)在E中的臨界點對應于方程組(1)的弱解．我們稱(u，v)∈E是方程組(1)的弱解，當且僅當對?(φ，ψ)∈E，都有

(7)

其中

引理2若{(un，vn)}?E是J(u，v)的(PS)c序列，則{(un，vn)}在E中有界．

證若{(un，vn)}?E是J(u，v)的(PS)c序列，則有

(8)

應用反證法，假設當n→∞時，有‖(un，vn)‖E→∞．下面將分3種情況進行討論：

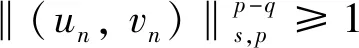
由此可知‖(un，vn)‖E有界，矛盾．

情形2 ‖(un，vn)‖s，p有界，‖(un，vn)‖s，q→∞．根據(8)式，可知

從而可知

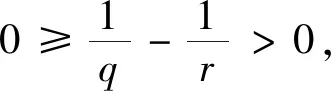
情形3 ‖(un，vn)‖s，p→∞，‖(un，vn)‖s，q有界．與情形2同理，矛盾．

引理3若{(un，vn)}?E是J(u，v)的(PS)c序列，且在E中有(un，vn)?(u，v)，則有J′(u，v)=0和J(u，v)>0．

證由文獻[11]的引理3.3可知，J′(u，v)=0，即

(9)

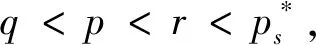
(10)

成立，那么泛函J在E中滿足(PS)c條件．

證設{(un，vn)}?E是J(u，v)的(PS)c序列，即滿足

(11)

(12)

由引理2和引理3可知，{(un，vn)}在E中有界，從而{(un，vn)}存在子列(仍記為{(un，vn)})，在E中有(un，vn)?(u，v)，且(u，v)是J(u，v)的一個臨界點．當n→∞時，有

un→u，vn→va.e.x∈RN

并且當n→∞時，由Lebesgue控制收斂定理可知

(13)

(14)

和

(15)

同時，對任意的(φ，ψ)∈E，若有

那么(u，v)∈E是方程組(1)的弱解，將(13)-(15)式代入(11)和(12)式，可得

(16)

(17)

不失一般性，設

由(5)和(17)式可知

(18)

這與(10)式矛盾，由此可知a=0，在E中有(un，vn)→(u，v)，引理4得證．

證證明與文獻[15]中引理4.1、引理4.2、定理1.2的證明類似．

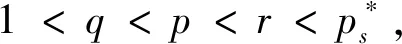
證顯然J(0，0)=0成立．由(5)和(17)式可知

因此，存在常數ρ，β>0，使得對所有滿足‖(u，v)‖s，p=ρ的(u，v)，都有J(u，v)≥β成立．

當t→∞時，J(tu，tv)→-∞，因此存在t0>0，使得當‖(t0u，t0v)‖s，p>ρ時，有J(t0u，t0v)<0．令(u0，v0)=(t0u，t0v)，則有成立．

Γ={γ∈C([0，1]，E)：γ(0)=0，γ(1)=e}

再結合引理4，可得泛函J的一個臨界點(u1，v1)，因為J(u1，v1)=c1>0，故(u1，v1)是方程組(1)的非平凡解．