基于卷積神經網絡的地下水磁共振數據隨機噪聲壓制方法

李 邦，蔣川東,2,3，王 遠,2,3，田寶鳳,2，段清明,2,3，尚新磊,2,3

1.吉林大學儀器科學與電氣工程學院，長春 130026 2.地球信息探測儀器教育部重點實驗室(吉林大學)，長春 130026 3.國家地球物理探測儀器工程技術研究中心(吉林大學)，長春 130026

0 引言

地面磁共振探測(magnetic resonance sounding，MRS)是一種非侵入式直接探測地下水的技術。和其他地球物理探測方法相比，MRS技術具有直接高效、信息量豐富、定量準確及解釋唯一的優點[1]。近年來，MRS技術還被應用到水污染監測、水文環境評價[2]和地質災害預警等領域[3]。

MRS信號微弱，僅為納伏級別，極易受到周圍環境中電磁干擾的影響，導致采集到的MRS數據質量嚴重依賴于測量地點的電磁噪聲水平。尤其在城市和村鎮這些人類活動較多的區域進行磁共振探測時，MRS信號被噪聲完全淹沒，信噪比極低，這使得MRS數據反演解釋的準確度嚴重下降[4]。同時這也是制約目前MRS技術大規模應用的主要瓶頸。因此，研究磁共振信號的噪聲壓制具有非常重要的意義。

根據噪聲來源和信號特征的不同，地面磁共振數據中的噪聲可被分為隨機噪聲、工頻諧波噪聲和尖峰噪聲3種。去除工頻諧波噪聲的方法有自適應濾波[5]和工頻諧波建模[6]等，去除尖峰噪聲可以用壓縮小波變換方法[7]，通過上述方法可以較好地去除這兩種噪聲。隨機噪聲的特征為高斯白噪聲，一般通過疊加多次測量數據取平均值的方式減小[8]。2018年，王琦等[9]提出基于稀疏表示的隨機噪聲背景下多弛豫MRS信號的提取方法。林婷婷等[10]使用時頻峰值濾波(time-frequency peak filtering，TFPF)方法，對隨機噪聲起到了良好的壓制效果。但上述兩種方法處理過程較為繁瑣，計算耗費時間長，對于野外實驗取得的大量數據難以實現實時處理，且仍不能完全達到滿意的噪聲壓制效果。

針對MRS信號隨機噪聲壓制中存在的上述問題，本文提出使用卷積神經網絡(convolutional neural networks，CNN)[11]對磁共振數據中的隨機噪聲進行壓制。本文首先介紹地面磁共振數據信號和噪聲的特征，以及基于CNN的MRS數據噪聲壓制的過程。然后，利用CNN對仿真MRS數據進行隨機噪聲壓制，并與TFPF方法處理的結果進行對比，證明CNN的優勢。最后，通過野外實測數據的MRS噪聲壓制結果，驗證了基于CNN的MRS數據隨機噪聲壓制方法的有效性和實用性。

1 原理與方法

1.1 磁共振信號及其噪聲特征

在發射線圈中通入Lamor頻率電流，向地下發射電磁場，地下水中的氫質子被電磁場激發，形成宏觀磁矩，這一宏觀磁矩在地磁場B0中以B0方向為軸進行旋進運動。自由感應衰減(free induction decay, FID)是核磁共振與磁共振成像中最簡單的信號形式。受激發的氫核對磁振頻譜儀或磁振造影掃描器的射頻線圈造成感應電流而產生信號，并因為發生弛豫而使信號強度逐漸衰減至0，這種逐漸衰減的信號即稱為FID。當激發場停止后，氫質子旋進產生弛豫現象；地面接收線圈記錄到的宏觀磁矩進動產生的電磁信號就是FID信號VFID，可表示為

(1)

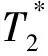
由于FID信號極為微弱，單位僅為納伏級別，要采集這樣的微弱信號就必須使用高靈敏度的接收器。因此，最終采集到的信號中包含了大量噪聲。

采集到的MRS數據可表示為

VMRS=VFID+Vrandom+Vspike+Vharmonic。

(2)

式中：Vrandom為隨機噪聲；Vspike為尖峰噪聲；Vharmonic為工頻諧波噪聲。由于尖峰噪聲和工頻諧波噪聲已經有了多種成熟有效的去除方式，因此本文僅對MRS信號中隨機噪聲的壓制展開研究。

1.2 MRS數據預處理

對采集到的數據進行尖峰壓制和工頻諧波建模消噪后，得到僅包含MRS信號和隨機噪聲的數據，對其進行希爾伯特變換，得到包絡信號(以單指數信號為例)的實部Vr和虛部Vi分別為：

(3)

(4)

式中：df為頻率偏量；εr與εi分別為噪聲的實部和虛部分量。

CNN善于提取二維信息中的特征[11-12]。為了使用MRS數據訓練CNN，首先利用式(5)對MRS信號E=Er+iEi(Er和Ei分別為MRS信號的實部和虛部)進行短時傅里葉變換 (short-time Fourier transform，STFT)：

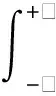
(5)

式中：τ和f分別為時頻譜的時間點和頻率點；ω(t-τ)為窗函數；X為神經網絡的輸入時頻譜。

圖1展示了純凈MRS信號和含噪MRS包絡數據經過STFT后的時頻譜[12-13]。可以看出，STFT的結果可以同時反映信號在時域和頻域上的分布。含有更多信息的二維時頻信號可以使神經網絡學習到更多MRS信號特征，提高噪聲壓制結果的準確度。

2 基于卷積神經網絡的噪聲壓制方法

CNN是一種多層的監督學習神經網絡，運行的機制是輸入層的數據在多個隱藏層中依次進行特征提取，最后在輸出層輸出，若輸出與理想結果偏差超過可接受的范圍，則調整隱藏層神經元的權重和偏置[13]。這樣根據輸入和輸出結果之間的關系，訓練得到一個最優的模型的方法，稱為監督學習。本文利用如圖2所示CNN結構。

網絡主要包含輸入層、卷積層、批歸一化(batch normalization，BN)層、激活函數層和輸出層。

卷積層通過將卷積核與輸入數據作卷積運算，提取輸入數據不同位置的局部特征。而通過設置平移步長，可以令卷積核分別提取數據不同位置的特征，最終得到輸入數據的特征圖(feature map)。卷積操作的公式為

C(i,j)=(X*W)(i,j)=

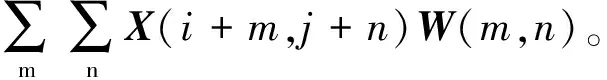
(6)

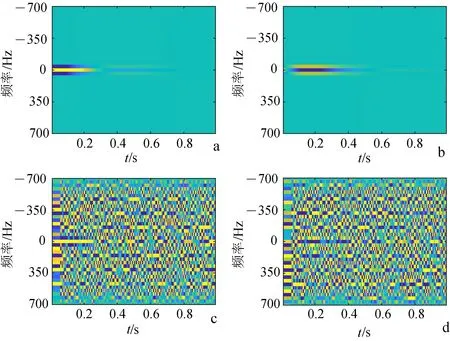
a. 純凈MRS信號的實部；b. 純凈MRS信號的虛部；c. 僅含隨機噪聲MRS信號的實部；d. 僅含隨機噪聲MRS信號的虛部。

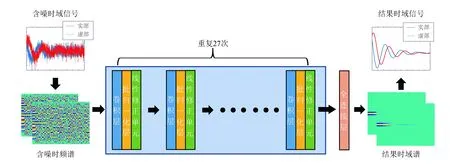
含噪時頻譜和結果時頻譜圖片前面的是實部，后面的是虛部(示意圖)。

式中：i、j、m、n分別為位置坐標；W為卷積核；*為卷積運算；C為卷積結果。

為了避免神經網絡的內協變量偏移，每層使用批歸一化方法[14]。批歸一化層在神經網絡層的中間進行預處理，即上一層的輸入經歸一化處理后再進入網絡的下一層，這樣可有效地防止訓練時發生梯度爆炸，并加速網絡訓練。每層卷積層均使用線性修正單元(rectified linear unit，ReLU)函數[15-16]作為激活函數。

CNN大多采用池化層對上一層的輸出特征進行下采樣以及對網絡引入平移不變性。本文研究內容為由輸入含噪時頻圖像得出純凈MRS信號的時頻圖像，由于訓練集中信號的頻率與測試MRS信號的頻率較為接近，訓練集和驗證集的時頻圖像出現位置相差不大，因此不需要用到池化層的平移不變性。基于以上兩點原因，本文構建了不含有池化層的CNN。

隱藏層中包含27個卷積層，每個卷積層后都設置一個批量歸一化層與激活函數層，共81層。不同卷積層所對應的神經元節點數在300～1 000不等。第一個卷積層使用了大小為9×8的卷積核，后續卷積層使用的卷積核大小為9×1與5×1。就如前文所述，卷積核大小為9×1的卷積層代替了池化層的作用。在隱藏層的最后，使用全連接(full connection，FC)層獲得神經網絡的輸出。

本文將純凈FID數據和去噪后數據的時頻譜之間的均方誤差(mean squared error，EMS)作為損失函數來訓練網絡參數：

(7)

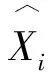
最后，我們采用Adam算子[17]最小化損失函數對網絡進行優化。

第二天一早，一看表，七點多啦！完蛋了，看來又得挨批了。我趕緊起床洗漱，一抬頭，哇！鏡子里那只“熊貓”是誰呀！都是蚊子惹的禍！唉，蚊子呀蚊子，你犯下的滔天大罪我會永遠記住的！

3 結果

3.1 實驗過程

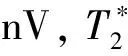
對訓練集數據的實部和虛部分別進行STFT，得到其時頻譜。實驗中STFT的窗寬設置為256，重疊率為0.75。為了降低神經網絡所需的運算資源，在進行訓練時，只取-700～700 Hz的時頻信息作為神經網絡的輸入和輸出。每一次訓練分別是以含噪信號的時頻矩陣作為網絡輸入，對應的純凈MRS信號的時頻譜作為輸出。

設置每次訓練的批次大小為512，初始學習率設置為10-3，每迭代4輪之后，學習率衰減為之前的1/2，一共迭代24輪。

本文訓練CNN所用的計算機配置為：CPU i5 8500，RAM 32 Gb。該計算機使用給定的訓練集對CNN進行訓練，總用時538 min。神經網絡模型一次訓練完成后，后續每次對MRS信號做噪聲壓制時只需把信號做STFT后，得到的時頻矩陣與神經網絡的參數矩陣做線性運算，這個過程僅需0.32 s，而TFPF方法耗時為6.89 s，相較之下極大節省了數據處理所需的時間。

3.2 基于CNN的MRS隨機噪聲壓制結果

使用訓練完成的CNN模型對隨機挑選的一組驗證MRS信號的噪聲壓制后，數據的信噪比為5 dB。從圖3a、b可以看出，經噪聲壓制之后的MRS信號與純凈MRS信號包絡能夠較好地吻合；由圖3c、d,3e、f與圖3g、h可以看出，經CNN噪聲壓制后的時頻譜與純凈信號的時頻譜基本相同，證明了CNN方法可以對MRS信號中的隨機噪聲起到良好的壓制作用且不存在MRS信號的能量損失。

3.3 噪聲影響

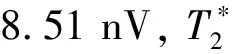
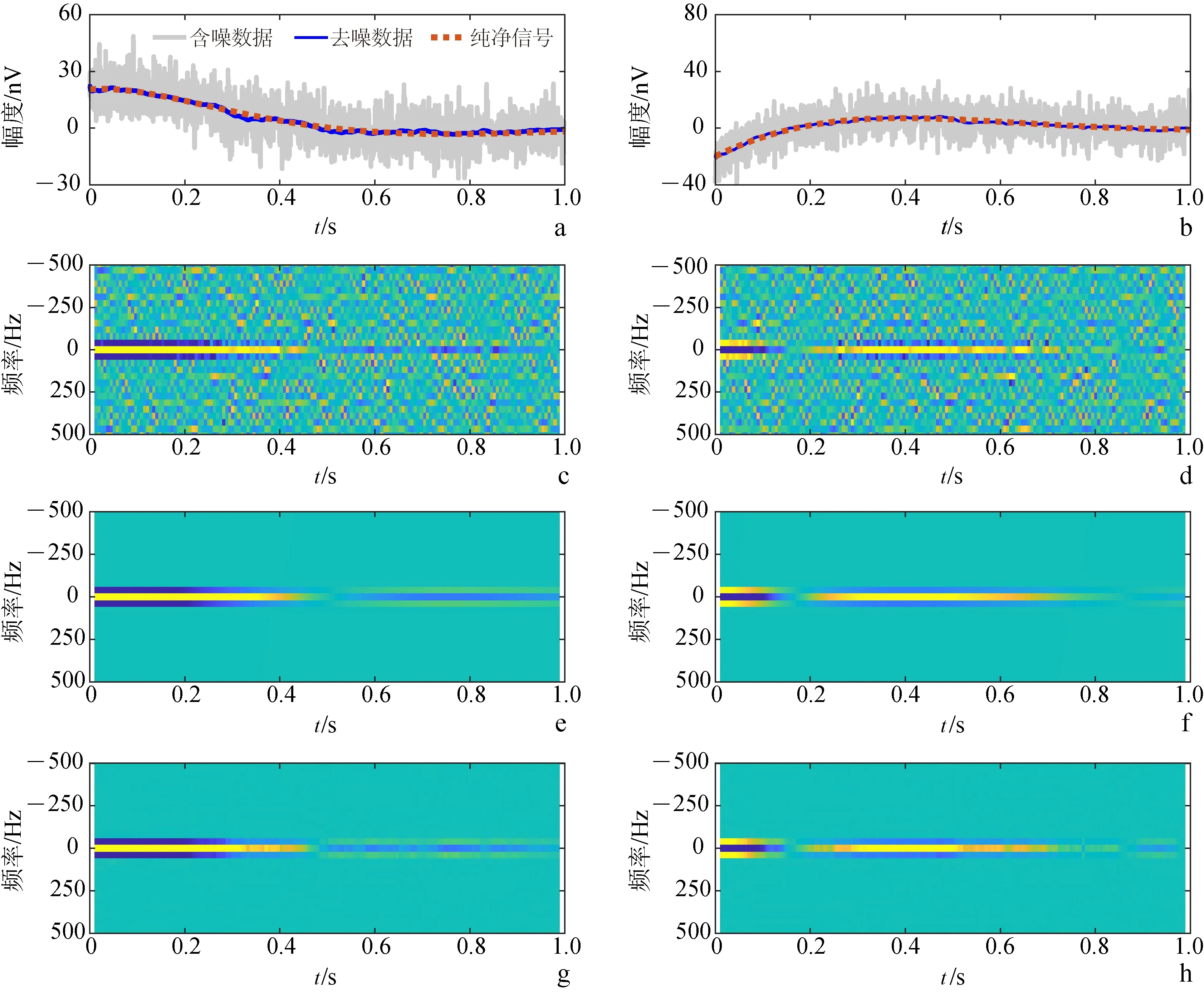
a. MRS數據實部的時域圖；b. MRS數據虛部的時域圖；c. 含噪數據實部的時頻譜；d. 含噪數據虛部的時頻譜；e. 純凈信號實部的時頻譜；f. 純凈信號虛部的時頻譜；g. 噪聲壓制后實部的時頻譜；h. 噪聲壓制后虛部的時頻譜。

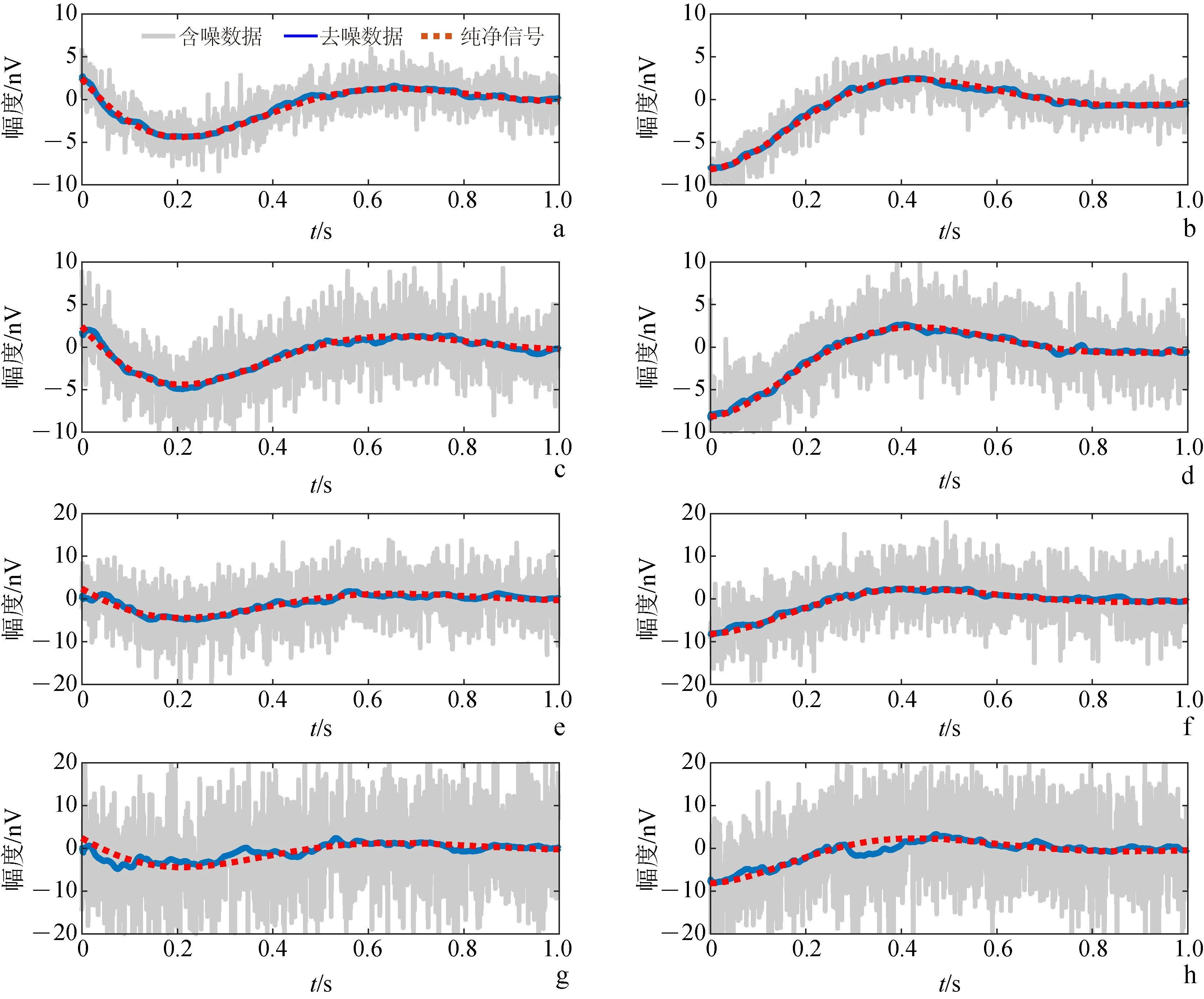
a. SNR=5 dB,實部；b. SNR=5 dB，虛部；c. SNR=0 dB，實部 ；d. SNR=0 dB，虛部；e. SNR=-5 dB，實部；f. SNR=-5 dB，虛部；g. SNR=-10 dB，實部；h. SNR=-10 dB，虛部。

由圖4可以看出，當信噪比大于等于-5 dB時，經CNN噪聲壓制后，實部和虛部的包絡曲線與純凈FID信號包絡(圖中紅色曲線)基本重合。當信噪比為-10 dB時，消噪后包絡曲線略有扭曲。

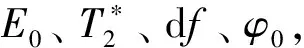
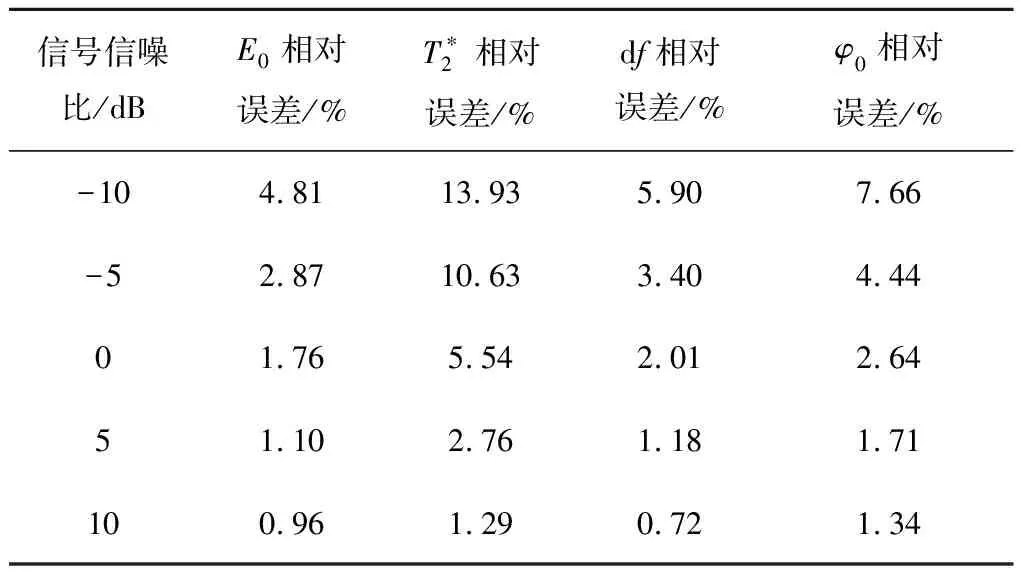
表1 CNN與TFPF單指數信號噪聲壓制結果參數擬合效果對比

3.4 CNN與TFPF對比

圖5為這1組多指數MRS信號加入不同水平噪聲后分別使用CNN和TFPF兩種方法進行噪聲壓制的結果。

由圖5可以得出，對于多指數MRS信號，當信噪比大于0 dB時，CNN和TFPF兩種方法均可以對噪聲實現有效的抑制。當信噪比小于-5 dB時，TFPF方法得到的包絡信號產生嚴重的失真，此時CNN方法的效果顯著優于TFPF方法。

針對不同信噪比，分別使用CNN和TFPF對不同信噪比情況下的100組仿真MRS數據進行噪聲壓制。單指數信號處理結果的信噪比和均方根誤差(root mean squard error，ERMS)見表2，多指數信號處理結果的信噪比和均方根誤差見表3。其中均方根誤差采用式(8)計算：

a. SNR=5 dB，實部；b. SNR=5 dB，虛部；c. SNR=0 dB，實部；d. SNR=0 dB，虛部；e. SNR=-5 dB，實部；f. SNR=-5 dB，虛部；g. SNR=-10 dB，實部；h. SNR=-10 dB，虛部。

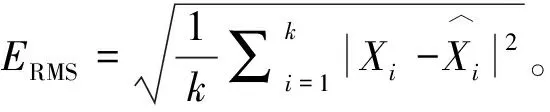
(8)

式中，k為時頻譜矩陣中元素數目。

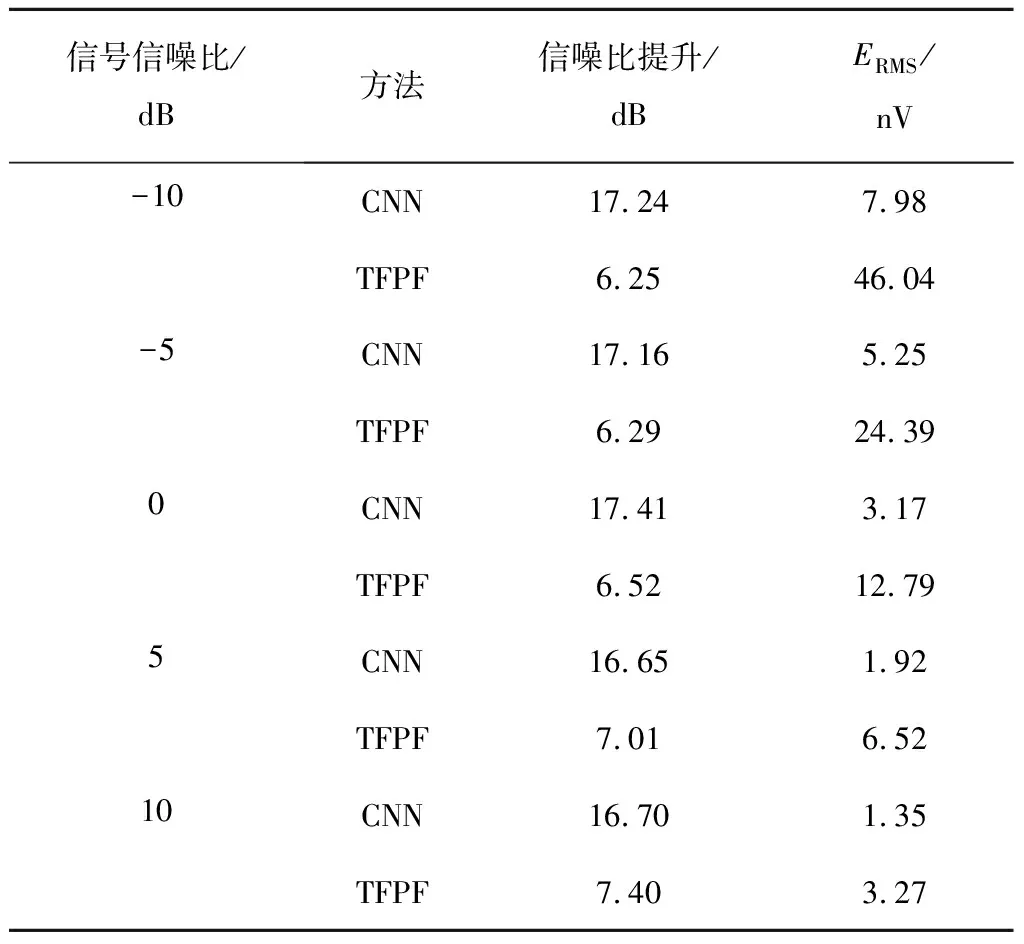
表2 CNN與TFPF單指數信號噪聲壓制結果信噪比和均方根誤差對比

表2和表3列出的數據表明：經CNN方法進行噪聲壓制后的信號擬合誤差相比TFPF方法的結果擬合誤差更低；在進行實驗對比的信噪比下，CNN的擬合誤差明顯低于TFPF。

另外可以看出，基于CNN和TFPF的兩種MRS隨機噪聲壓制方法，在信噪比高于0 dB時，均可有效地壓制噪聲，其ERMS均小于20 nV。在信噪比低于0 dB時，CNN方法的ERMS仍小于20 nV，而TFPF方法的ERMS已經高于20 nV。整體來看，CNN方法噪聲壓制結果的信噪比提升量在各個場景下都比TFPF方法高出8～11 dB，而CNN處理結果的ERMS值比TFPF方法降低了59%～82%。由此可以得出：CNN進行噪聲壓制后的MRS仿真信號信噪比獲得了提升，且信噪比提升效果明顯優于TFPF方法處理的效果。以ERMS作為評估指標時，CNN處理結果擁有更低的ERMS值，效果同樣優于TFPF方法。

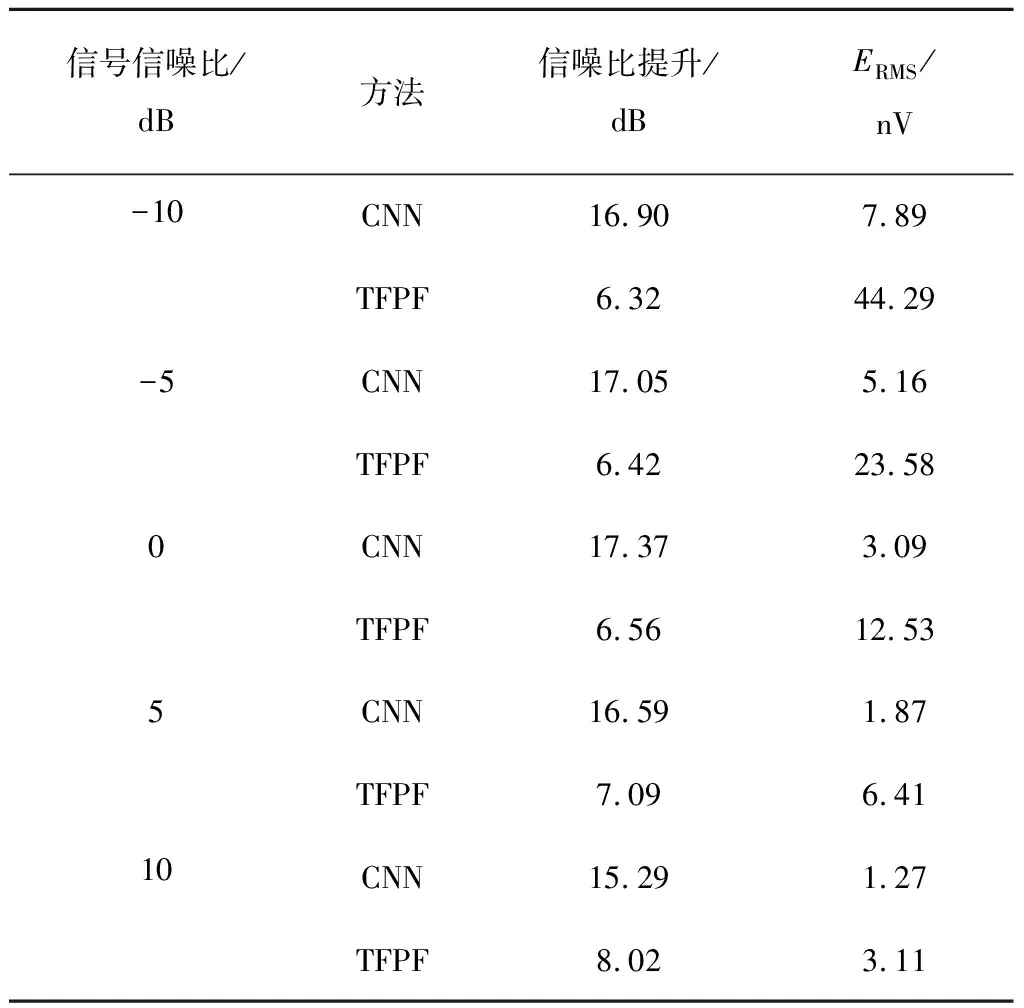
表3 CNN與TFPF多指數信號噪聲壓制結果信噪比和均方根誤差對比

3.5 野外實測數據驗證

為了驗證本文設計的CNN對實際采集MRS信號進行隨機噪聲壓制的有效性，在吉林省長春市燒鍋鎮進行了MRS探測實驗，探測點附近均為農田和樹林，地勢平坦，且臨近水庫，具有豐富的地下水資源。野外實驗數據使用JLMRS-IV型磁共振地下水探測儀獲得，測量地點的地磁場強度為54 908 nT，Larmor頻率為2 338 Hz，地磁傾角為60°，發射/接收一體線圈的尺寸為100 m×100 m，使用不同發射脈沖矩測得16組MRS信號。以實測磁共振信號作為研究對象，并與TFPF方法作比較。圖6展示其中一組測量信號的噪聲壓制結果。

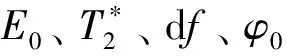
4 結論

1)為了克服隨機噪聲給磁共振反演解釋帶來的問題，本文設計了用于壓制MRS信號中隨機噪聲的CNN，并使用仿真數據和實測數據做了驗證。

2)使用CNN對單指數/多指數MRS信號進行噪聲壓制時均能取得良好的效果。與TFPF方法進行對比，CNN的噪聲壓制效果更優秀。

3)通過野外實測數據驗證，得到了和仿真實驗相同的結論，證明了此方法在實際工程應用中的價值。