“雙減”背景下初中數學作業的設計與批改

摘 要:作業的設計及批改是關系“雙減”政策背景下減輕學生作業負擔的關鍵因素。也就是說,有效的數學作業設計及批改方式的應用直接影響著“量”到“質”的轉變。所以,在“雙減”政策背景下的初中數學教學過程中,教師要將“設計”與“批改”整合在一起,充分發揮學生的學習主動性,使學生在靈活運用所學知識分析問題及解決問題的過程中真正形成基本的數學學習能力。
關鍵詞:初中數學;作業設計;作業批改
中圖分類號:G427 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼:A ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文章編號:2095-9192(2022)17-0091-03
引 ?言
作業是檢驗學生課堂學習情況的重要手段,更是鞏固所學知識的有效方式之一。但是,在以往的教學過程中,大多數教師選擇的是“題海戰術”,通過組織學生完成大量的試題來豐富學生的“見題”面,導致學生的學習壓力越來越大。為了解決這一問題,2021年7月國家提出了“雙減”政策,目的就是減輕學生的作業負擔,降低學生的課業壓力。所以,如何在這樣的大背景下實現減負增效的目的也就成了一線教師重點思考的問題。本文從“作業設計”“作業批改”兩個大方面入手對如何實現提質增效的目的進行論述。
一、作業設計
(一)基礎類作業的設計
基礎類作業是指掌握基礎知識時需要完成的作業,基礎類作業的設計是“雙減”政策背景下減輕學生作業數量的關鍵部分。為了能夠達到減負增效的目的,在初中數學作業的設計中,教師可以遵循分層原則,通過設置不同層次的作業來達到提高學生作業效率的目的,為減輕學生的作業壓力打好基礎[1]。
以“三角形全等的判定”這一節內容為例,由于這部分內容主要的教學目的是讓學生掌握基本的三角形全等的判定定理,并能靈活運用,所以,在進行作業設計時,教師分了三個層次。
A層:基礎層
這部分作業主要是打基礎的,也是針對一些基礎較差的學生設計的,目的是幫助他們打好基礎,再進行一步步的改進。因此,教師設計了如下作業。
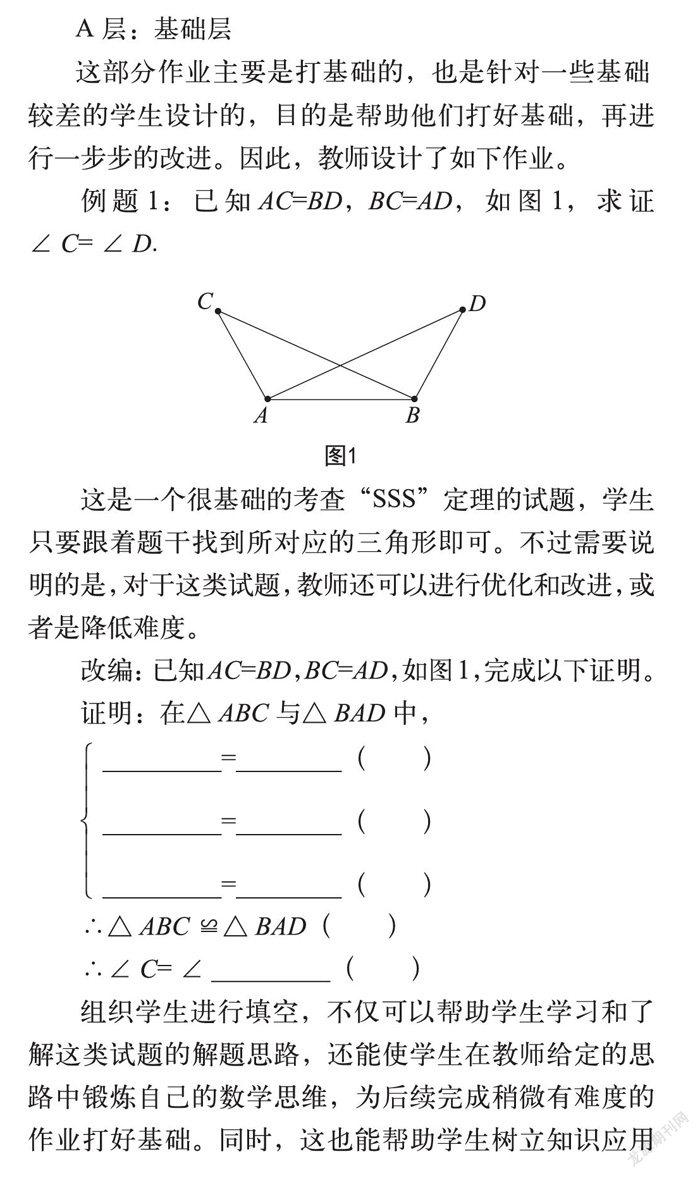
例題1:已知AC=BD,BC=AD,如圖1,求證∠C=∠D.
這是一個很基礎的考查“SSS”定理的試題,學生只要跟著題干找到所對應的三角形即可。不過需要說明的是,對于這類試題,教師還可以進行優化和改進,或者是降低難度。
改編:已知AC=BD,BC=AD,如圖1,完成以下證明。
證明:在△ABC與△BAD中,
∴△ABC≌△BAD( )
∴∠C=∠_________( )
組織學生進行填空,不僅可以幫助學生學習和了解這類試題的解題思路,還能使學生在教師給定的思路中鍛煉自己的數學思維,為后續完成稍微有難度的作業打好基礎。同時,這也能幫助學生樹立知識應用的意識,有助于后進生的轉變。
B層:中等層
這一層次的作業主要是針對中等生,且這部分學生劃分的范圍要大一些。作業本身就是為了鞏固所學,鍛煉學生的思考能力,所以,教師可以將大部分學生劃歸到這一層次,確保每個學生都能在思考交流中掌握知識。
例題2:已知AD=CE,∠A=∠E,BC∥FD,如圖2,求證:AB=EF.
例題3:已知∠1=∠2,∠ABC=∠DCB,如圖3,
求證:AC=BD.
通過這兩道題可以看出,例題2的難度要比例題3的難度小一些,基礎層的學生可以嘗試完成例題2,但中等層的學生都要完成。此外,從這兩道例題的設計來看,學生并不能簡單找到與某一個判定定理有關的已知量,需要進行一些思考,引入一些之前學過的知識。比如,對于例題2來說,在該題的解答過程中,學生要思考BC∥FD能夠得到哪些結論,AD=CE能夠得到什么結論,需要求證的AB、EF分別在哪兩個三角形中等。這些都需要學生通過思考找到證明的思路。
C層:拔高層
拔高層作業設計的綜合性要強一些,要鍛煉學生的綜合知識應用能力[2]。當然,中等生也可以嘗試做,但不強制。
例題4:已知△ABC是等腰三角形,D是邊AB上一點,DF交AC于點E,∠ADE=∠F,DE=FE,如圖4,求證:AC-FC=BD.
從該題的解題思路來看,該題不僅考查三角形的判定定理,還考查等腰三角形的性質、平行線的判定等,綜合性相對強一些。當然,對于分層作業的完成來說,基礎層的學生在完成本層的作業后,可以嘗試完成中等層的作業,中等層的學生如果感覺自己哪部分知識掌握得不牢固也可以在基礎層作業中進行挑選練習。每個層次之間的作業是相對的,并不是絕對的。
(二)能力類作業的設計
能力類作業的設計主要是為了鍛煉和提高學生的知識應用能力,并使學生在知識應用中思維得到發散,能力得到鍛煉,是建立在基礎類作業的基礎上,也是提升學生數學素養不可缺少的。所以,在能力類作業的設計中,教師除了要培養學生的問題思考能力,還要通過一題多變、一題多解等來發散學生的思維[3]。
以上文提到的例題3為例,該題有多種解答方式,所以,在設計能力類作業的過程中,教師不妨鼓勵學生對所要完成的練習進行進一步的思考。具體如下。
解法一:通過證明△ABC≌△DCB來證明AC=BD;解法二:通過證明△AOB≌△DOC來證明AC=BD。具體如圖5。
這一問題的解法還有很多種,學生要大膽借助自己所學的知識尋找已知量與未知量之間的關系。同時,為了鍛煉學生的知識應用能力,提高學生的解題能力,在該題的基礎上,教師可以布置“一題多變”的試題,讓學生自主結合網絡資源或者課外材料來進行創編,這也是鍛煉學生創編能力的過程,具體如下。
變形一:在△ABC和△DCB中,已知:∠A=
∠D=90°,AC=BD,AC和BD的交點為O,如圖6,求證△OBC是等腰三角形。
變形二:在△ABC和△DCB中,請從下面三個條件中選擇兩個為題設,第三個作為結論,并加以證明。(可以嘗試寫出多種)
①AB=DC;②AC=DB;③∠ABC=∠DCB。
從這些試題的設計來看,學生可以通過變式的思考及交流達到鍛煉和提高解答問題能力的目的。從初中數學的一些基礎練習中,我們也可以知道,這張圖的應用是比較廣泛的。所以,在組織學生進行練習時,教師要充分發揮學生的主動性,從多角度引導學生思考,幫助學生對這張圖有比較全面的認識。
(三)實踐類作業的設計
實踐類作業的設計主要是將數學與學生熟悉的生活結合在一起,讓學生在實踐應用中感受數學的應用價值。但是,這類作業的設計難度要大一些,不僅要緊密地結合教材內容,還要具有可操作性,確保學生在實踐應用中調動數學學習積極性。
以“數據的分析”為例,為了培養學生的數學運算能力,也為了讓學生感受到數學與生活之間的緊密聯系,教師可以設計下面的作業。
以小組為單位自選50名學生來進行身高的調查,并做出相關的分析。
從這一作業的設計來看,有以下幾點需要注意。首先是“自選”,學生可以選擇某一個班的50名學生,也可以隨機選擇50名學生。其次是學生需要自主進行分析。這個分析里不僅要制作直方圖,還要計算出中位數、平均數、眾數等。總之,要將這一單元所學知識都拿來進行分析,并對數據所反映的情況進行明確。
綜上,不難看出,不同類型的作業所達到的目的也不一樣。在教學過程中,教師要做好教材內容的挖掘工作,逐步落實“雙減”政策,這也有助于實現提質增效的目的。
二、作業批改
批改是作業中的一部分,其作用與設計布置是同等重要的,所以,在“雙減”政策背景下,教師除了要做好作業的設計與布置,還要注重批改活動的開展。
(一)學生互批
所謂學生互批是指雙方或者多方就作業的對錯、方法、過程等進行評價,是幫助學生鍛煉分析能力、鞏固基礎知識的有效方式之一。所以,在批改環節,教師要充分發揮這一批改方式的作用,使學生的學習效率得到大幅度提高。
還以上文提到的“分層作業”設計為例,我們都知道這類作業是將學生進行了分層,而學生之間的互批是可以增強這類作業的實施效果的。具體來說,在互批中,拔高層的學生批改中等層學生的作業、中等層學生批改基礎層學生的作業。由于中等層學生相對較多,在批改時,可以小組為單位共同批改。不過需要說明的是,在批改的過程中,學生要做好批注,指出哪里出錯了、如何糾正等。總之,教師要將主動權交給學生,但也要幫助學生明確批改活動的目的,這樣才能真正發揮學生互批的作用。
(二)小組長批改
小組長批改是指以合作學習小組的形式來開展批改活動,在這個過程中小組長非常關鍵,因為小組長需要進行批改,之后與組員、教師進行交流、互動,幫助組內成員學習。
以上文提到的例題3為例,在這道例題的設計中,教師除了要求中等生進行基礎解答,還可組織拔高層次的學生進行“一題多解”“一題多變”。在組織小組長批改的過程中,教師首先要按照學生的情況將其分成不同的批改小組,且每個小組內要包含各層次的學生,由小組長負責批改,其他學生要對這些試題進行思考。在批改后,小組成員進行討論,比如,該題的考查點都包含哪些?該學生提出了幾種問題解答的方式?分別是怎樣的?是否還有其他的問題解答方式?出錯率最高的點在哪里?總之,充分發揮小組的作用,確保學生在交流思考中對該題有一個全面的認識,可以使學生在這樣的批改中加強認識,提高效率。
結 ?語
作業的設計與批改是“雙減”政策背景下一線數學教師亟須解決的問題,也是重點需要思考的問題。在數學作業設計與批改的過程中,教師要充分發揮學生的主動性,確保每類試題的價值都能發揮到最大,真正實現減負增效的目的。
[參考文獻]
陳傳東,趙蘭,王浪.“雙減”背景下初中數學作業的批改與輔導[J].教學與管理,2022(10):39-41.
薛潔.初中數學作業現狀與應對策略研究[D].重慶:西南大學,2020.
李柳花.初中數學作業分層設計的研究[J].科學咨詢(科技·管理),2020(07):167.
作者簡介:劉加慶(1976.9-),男,福建南安人,任教于福建省泉州市南安國光中學,中學一級教師,本科學歷,南安市優秀教師,南安市教研積極分子,泉州市優秀班主任,南安市數學學科帶頭人。

