反思解題再生習題資源，有效提升初中生數學解題能力

李曉玲

[摘? 要] 數學學習不僅要重視解題，更要重視解題后的反思和回顧. 在教學過程中教師通過解題反思和總結的教學活動，培養學生自主學習和自主歸納的能力，讓學生在獨立思考、自主探究的過程中不僅知其然，更能知其所以然，體會解題思路和方法，有效提升解題能力.

[關鍵詞] 解題反思;習題資源;解題能力

數學課程給人的傳統印象是解題，注重解題的結果和結論的獲得，而結論形成的過程卻常常被忽略，以至于學生只記住了結論，不知道結論的由來過程，影響了學生學習能力的提升. 長此以往，造成部分學生習慣用記憶結論和模仿解題方法的方式進行學習，失去分析和探究問題的能力，不利于學生的長期學習和發展. 數學課程的教學不僅要關注解題結果，更要關注解題后的反思，處理好解題過程與結果之間的關系，才能真正激發學生的學習興趣，讓學生理解數學的本質和內涵. 筆者在教學中嘗試從解題后的再認識和再創造，引導學生進行思考，探究試題的考查意圖，總結解題方法，尋找解題規律，有效提升學生的解題能力.

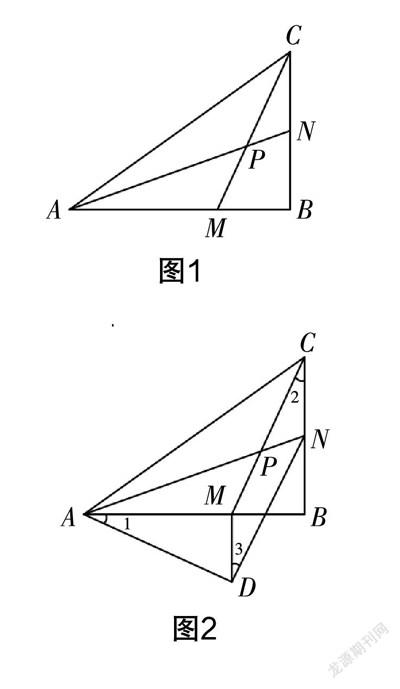
案例? 如圖1，在△ABC中，∠B為直角，AB上有一點M，并且AM與BC相等，BC上有一點N，并且CN與BM相等，AN與CM相交于點P，求∠APM的度數是多少？

通過測量或者觀察分析可以猜想出結論：∠APM=45°.

解法1? 如圖2，過點M向△ABC外作MD平行于CN，并截取MD與CN相等，連接DN與AD，因為四邊形CMDN是平行四邊形，所以DN與MC相等且平行，∠2與∠3相等. 又因為∠B為直角，MD平行于CN，所以MD與AB垂直. 因為CN與BM相等，MD與CN相等，所以BM與MD相等. 又因為AM與BC相等，所以△AMD與△CBM全等，所以AD，MC，DN相等，∠1，∠2與∠3相等，又因為∠1與∠ADM的和為90°，所以∠3與∠ADM的和為90°，即∠ADN為直角，所以△AND為等腰直角三角形，∠AND為45°. 因為DN與MC平行，所以∠APM與∠AND相等為45°.

那么這道題是否還可以利用圖形變換的知識，尋找更多的解法呢？

反思考查意圖，尋找多種解法

通過這樣的解題方法，引導學生反思試題的考查意圖、考查的知識點和數學思想以及構成的條件與試題背景之間的關系，找到考查的核心數學模型是等腰直角三角形. 通過觀察和分析，添加了輔助線將AM與BC相等，CN與BM相等，進行有效利用，通過轉換和平移的方式，構造出新的圖形即平行四邊形以及全等三角形，就可以得到等腰直角三角形. 通過解題后的反思，學生發現了一種全新的解題方法.

思路一：利用等量轉換

通過圖形的平移將相等的角或者線段進行等量轉換，將已知條件與求證問題之間構建起聯系，從而尋找解題思路. 本題就是將所求的角轉換到一個等腰直角三角形當中，從而求得角的度數.

解法2? 如圖3，過點A作AD與BC平行，取AD與CN相等，連接CD和MD構造出平行四邊形ADCN，并且出現全等△MAD和△CBM，從而得到等腰直角三角形DMC，可以得出∠APM與∠DCM相等為45°.

在反思中交流，進行歸納總結

解題結果的完成并不是真正完成了解題過程，解題之后還需要組織學生進行相互交流，將自己分析的思路和解題方法進行表達，生生之間互相傾聽解題分析，將各種解題方法進行對比、分析和評價，互相取長補短，實現優勢互補. 這樣可以使學生加深解題過程的印象，也能培養學生的表達能力和合作能力，促進學生共同進步，協調發展.

思路二：利用圖形的位置變化

圖形可以通過平移、旋轉等方式改變位置，但是不改變形狀，從而實現有關角或者線段位置的變化，實現已知條件與所求結論之間的聯系，進而找到解題的方法和策略. 本題中，為了構建所求的角與已知條件之間的關系，可以通過圖形的旋轉變化進行新的圖形構造.

解法3? 如圖4，△ABC以點C為中心進行旋轉，將CB進行順時針90°旋轉到CD，連接AD和DN，由此可以得到CD，CB與AM相等，CD與AB平行，這樣可以構造出平行四邊形CDAM和全等三角形，△DCN與△CBM全等，從而得到等腰直角三角形DAN，由此可以得出∠APM與∠DAN相等為45°.

通過上述幾種解題方法的探討可以看到，這些解法都需要用到“添加輔助線構造圖形”的方法，這種“特別”的解法都圍繞著角和線段的等量變換進行展開，運用到圖形變化的多種方式，如平移、旋轉、翻折等，通過改變圖形的位置，在求答問題與已知條件之間構建聯系，使結論與條件之間的關系充分顯現出來，從而獲得解題思路. 這樣的變化是解題過程中常用的技巧，需要學生能夠熟練掌握并強化，需要教師通過多種方式不斷訓練學生，使學生能夠非常熟練地掌握這一解題的策略.

在解題之后反思解法，總結

成敗經驗

解題之后我們還常常需要反思剛剛的解題方法是否是最優解法，有沒有更好的解法，解題方法是否需要進行改進等. 在進行復雜題型的解答時，我們并不能一開始就找到最佳的解法，因此需要在解題過程中不斷地調整，以求找到最佳的解題路徑. 因此在解題之后進行回顧，尋找最優解法，從而思考是否抓住問題的關鍵，反思解題過程，拓展學生思維，鍛煉學生思維的靈活性和發散性，培養學生創新意識.

經過上述方法進行思考，學生又發現了另外一種解題方法.

解法4? 如圖5，過點A作AF與AB垂直，過點M作EM與AB垂直，過點C作FC與BC垂直，三條線的交點分別有點F和點E，由此得到矩形ABCF和正方形AMEF，再在CF上截取CG與CB相等，連接GN和GA，得到全等△GCN和△AFG，以及平行四邊形AMCG. 這一解題方法與解法3的方法類似.

由此可以得到等腰直角三角形GAN，得出∠APM與∠GAN相等為45°.

這一解題方法較為煩瑣，需要構造全等三角形和平行四邊形，但是圖形中由于有兩個正方形，因此給了我們一些啟示，那就是正方形的對角線可以平分對角得到45°，從而使得解法4能夠找到另外一條解題思路. 通過相似三角形的對應角相等，再進行相應的轉化就可以找到解題的結論，得到解法5.

思路三：利用相似圖形進行變化

圖形的相似變換需要利用數學性質或者概念中有關角或者線段進行位置轉化，實現等量轉換，從而在求答問題與已知條件構建聯系，進而尋找解題思路.

解法5? 如圖6，過點M作EM與AB垂直，過點C作EC與BC垂直，交點為點E，連接AE和EN. 因為四邊形MBCE是矩形，所以EC，BM相等，EM，BC相等，又因為AM與BC相等，BM與CN相等，所以△AME和△NCE是等腰直角三角形. 這樣可以得到兩個底角∠AEM和∠CEN都等于45°. 所以EM與AE的比值與EC和EN的比值相等，都等于. 又因為∠AEN等于∠AEM與∠MEN的和即∠CEN與∠MEN的和為90°，則∠AEN與∠MEC相等. 所以△AEN與△MEC相似，∠1與∠2相等. 因為∠3與∠4相等，所以∠AEM與∠APM相等為45°.

在反思中進行拓展延伸，總結規律

經過解法5的嘗試，我們可以聯想到其中經常使用到的一種解題方法，即兩個正多邊形如果共頂點，那么其對應頂點的連線的夾角正好等于其內角. 因為兩個正多邊形的邊若相等，那么這兩個正多邊形相似，其對應的頂點連線的夾角就等于其共頂點的角.

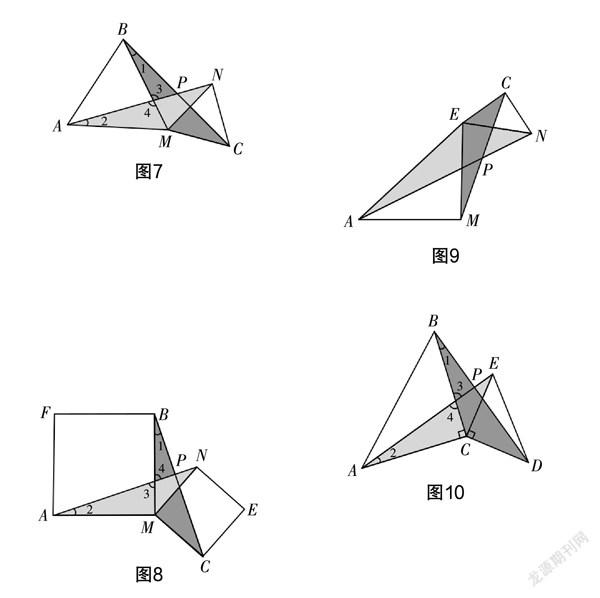
如圖7，正△ABM和正△CNM，連接BC與AN相交于點P，那么可以得到∠APB為60°.

如圖8，正方形AMBF和正方形CENM，連接CB和AN相交于點P，可以得到直角∠APB. 觀察圖8，可以證明△BMC和△AMN為相似三角形或者全等三角形，得到對應的∠1與∠2相等. 又因為∠3與∠4相等，所以∠APB與∠AMB相等.

因此可以進一步探究：兩個等腰直角三角形共頂點，那么這兩個等腰直角三角形相似嗎？如圖9和圖10，可以發現其對應頂點的連線夾角也等于共頂點的角.

觀察圖9，等腰直角△AME和等腰直角△NCE相似，可以得到AE與EN的比值與ME和CE的比值相等，由∠AEM與∠NEC相等，可以得到∠AEN與∠MEC相等. 所以△AEN與△MEC相似，∠1與∠2相等. 因為∠3與∠4相等，所以∠APM與∠AEM相等為45°.

運用同樣的解題方法可以得到圖10中∠APB，∠ACB為直角.

由此可以得到進一步的猜想：兩個三角形相似，其中有一對對應頂點為共點，那么另外兩組對應頂點的連線的夾角與共頂點的對應角度數相等.

……

綜上所述，解題之后反思試題本質，將題目的條件進行變化和聯想，在圖形變化中通過多種解法的運用，能鍛煉學生的思維能力. 習題的反思和圖形的變化，不僅在于探討多種解法，更重要的是通過不同解法的探究，發展學生思維的靈活性. 通過解題反思，進行解題方法共性總結，可以總結規律，歸納解題方法，由特殊到一般，使學生的思維更加廣闊，在探索中感受數學的魅力.