基于納什議價博弈的微電網一體化電站分布式協調優化

程杉， 尚冬冬， 魏昭彬， 倪凱旋

(1.三峽大學 電力系統智能運行與安全防御宜昌市重點實驗室，湖北 宜昌 443002； 2.國網重慶市電力公司北碚供電分公司，重慶 400000)

0 引 言

燃油機動車等移動源污染已成為我國大氣污染的重要來源，大力發展電動汽車勢在必行[1]。作為電動汽車電能補給的核心基礎設施，充換電站(battery charging-swapping station, BCSS)的投資、規劃和運維備受矚目。將BCSS中退役下來的動力電池作為儲能電站(energy storage station，ESS)的儲能電池，組成CSSIS，可實現電池的二次利用，并進一步增強CSSIS的供電能力[2]。將CSSIS和可再生能源發電以及其他負荷組成一體化電站微電網(integrated station microgrid, ISMG)，不僅可以顯著降低兩者單獨接入電網造成的不良影響，而且還能減小儲能成本，提高可再生能源利用率[3-4]，實現優勢互補，互利共贏。

當前很多文獻對含換電站(battery swapping station,BSS)或CSSIS的微電網經濟運行展開研究。文獻[5-6]提出了含BSS的微電網經濟運行模型，文獻[7-8]提出CSSIS的框架，但未將其與微電網進行結合以實現兩者優勢互補，而文獻[9]則研究了基于機會約束規劃的含CSSIS的微電網經濟調度問題。隨著售電側改革加深，微電網與CSSIS或BCSS很可能歸屬于不同利益主體，文獻[10]據此以微電網和BSS各自收益最大為目標函數，構建了微電網經濟調度雙層優化模型，但其計算效率有待提高。

在不同主體之間的策略和價格制定方面，Stackelberg博弈具有高效的求解能力。文獻[11]將電網與電動汽車電能交易過程構建為Stackelberg博弈模型，不僅平抑了電網負荷波動，還提升了電動汽車收益。考慮到電動汽車可促進可再生能源消納，文獻[12-13]利用KKT條件將運營商與電動汽車的Stackelberg博弈模型轉化為含整數的線性規劃問題進行求解，促進了新能源的消納，提高了電動汽車和分布式能源在參與電網能量交易中的經濟收益。文獻[14]基于Stackelberg博弈建立了CSSIS和微電網交互模型。上層微電網作為領導者制定交互電價；下層CSSIS作為跟隨者根據交互電價調整調度計劃，以上下層各自利益最大迭代求解直至達到Stackelberg均衡。

上述基于非合作博弈的方法使博弈參與者能夠獨立且經濟有效地做出決策。然而，這些策略未充分發揮博弈雙方之間存在的潛在合作可能性，因此通常得到的是非帕累托最優解[15-17]。同時，非合作博弈的納什均衡解一般不是交互系統社會最優解[18-19]，而合作博弈正好可以有效改善這一問題。作為合作博弈的一個分支，納什議價理論同樣適用于該問題，并能提高群體交互效益。基于納什議價理論，文獻[20]建立了配電網與微電網之間的經濟互動模型，參與者相互協調最小化爬坡率，文獻[21]則通過促進配網公司與需求響應聚合商這兩個非合作博弈參與者之間的合作，提高雙方收益。考慮到電動汽車充、放電管理，文獻[22]考慮光伏陣列、電動汽車以及居民負荷三方建立靜態合作博弈模型，采用Shapley值對合作利潤進行分配，但是并不能保證分配結果位于核中[23]。

基于上述文獻提及的不足之處，本文研究ISMG中微電網與CSSIS之間的能量交互策略。首先介紹ISMG的非合作博弈和合作博弈模式。需要著重指出的是，本文中的非合作博弈模式是基于文獻[14]中的Stackelberg博弈模型及其求解方法，而合作博弈模式則是在該Stackelberg博弈模型基礎上引入納什議價博弈模型，然后利用交替方向乘子法(alternating direction method of multipliers,ADMM)對納什議價模型中耦合變量進行解耦并迭代式求解。在合作博弈模式中，微電網與CSSIS之間只需共享交互功率即可求解該合作調度模型，得出納什議價解，從而有效保護博弈參與者隱私。本文最后通過對比分析非合作博弈模式和合作博弈模式下算例結果，驗證所提方法的可行性和高效性。

1 一體化電站微電網交互模型

1.1 系統結構

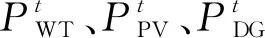
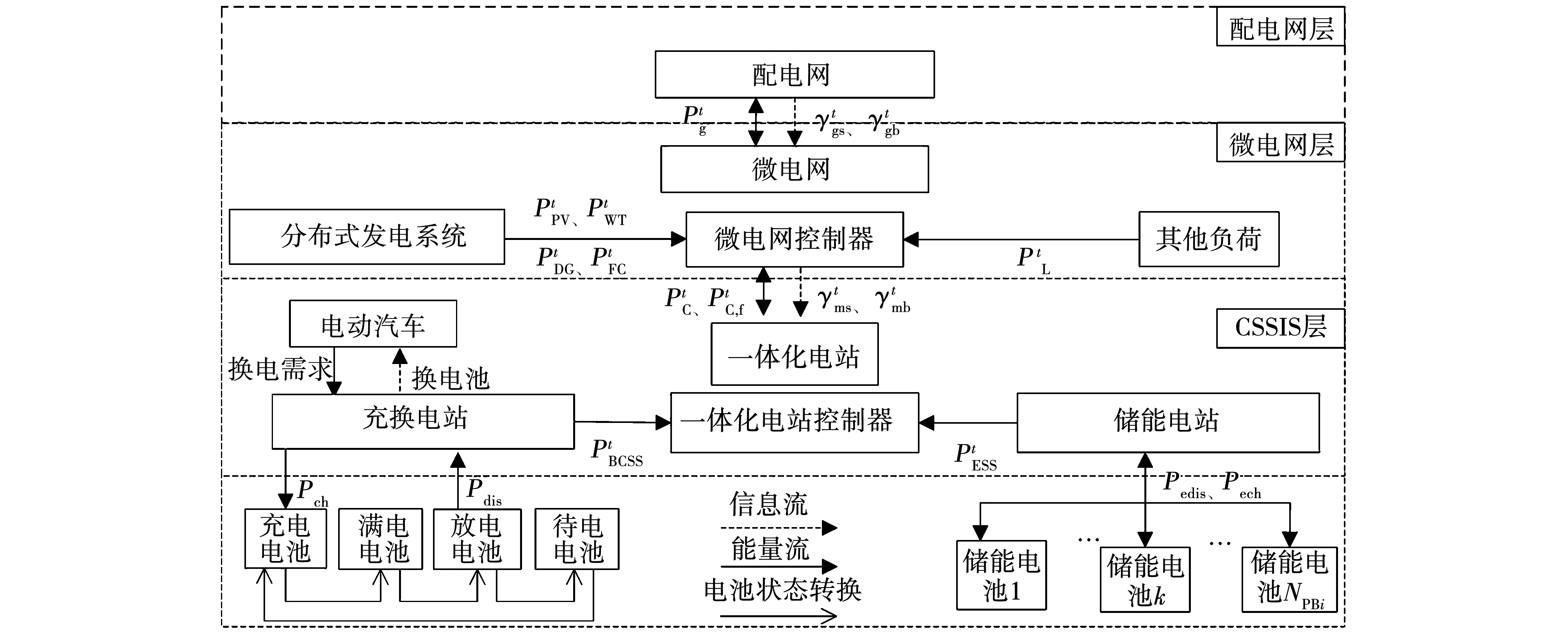
圖1 ISMG信息與能量交互框架

1)非合作博弈模式：以Stackelberg博弈為基礎構建兩者交互模型。上層微電網作為領導者，制定與下層CSSIS交互的內部電價；下層CSSIS作為跟隨者，根據上層發布的內部電價調整自身充放電計劃。上下兩層追求各自利益最大化，據此博弈，循環迭代直至達到Stackelberg均衡。

2)合作博弈模式：以納什議價博弈為基礎構建兩者交互模型。微電網通過給予CSSIS一定補償，令其更改充放電計劃，促使交易雙方達成合作。交易雙方經過協商對補償價格討價還價確定交互功率，循環迭代直至達到納什議價解，使整個系統社會收益最優。

1.2 微電網經濟運行模型

1)目標函數。

結合WT、PV和CSSIS出力值，制定FC和DG的出力計劃，以最大化微電網收益UMG為目標：

maxUMG=CExch-Ccost。

(1)

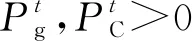
(2)

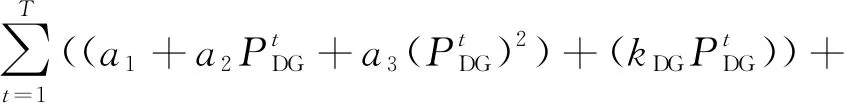
(3)

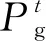
2)模型約束條件。

(4)

(5)

(6)

(7)

(8)

(9)

(10)

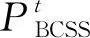
1.3 CSSIS經濟運行模型

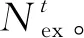
CSSIS根據微電網制定的內部電價信號協調自身充放電計劃，最大化CSSIS收益UCS，即

maxUCS=CR+UC-Cpay。

(11)

其中：CR表示CSSIS換電和售電收入之和；UC表示CSSIS電能消耗的滿意度；Cpay為CSSIS總支出。CR、UC和Cpay具體計算方法為：

(12)

(13)

(14)

其中：γ為單位電動汽車電池更換費用；en、dn表示CSSIS電能消耗的偏向因子，其可影響電力用戶對電能的需求程度；kom為CSSIS運維系數。

CSSIS需要滿足的約束條件如下：

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

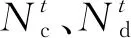
2 納什議價合作模型

假設分屬不同利益主體的微電網、CSSIS在選擇交互方式時是獨立且理性的。假設將非合作博弈模式中Stackelberg博弈的均衡解作為納什議價博弈初始分歧點，則該模式中滿足Stackelberg均衡唯一性條件[24-25]。假設微電網調度機構能意識到非合作博弈模式中Stackelberg博弈的均衡解不能達到社會最優，仍然存在利潤增加的可能性，則只要微電網提供的補償能夠使CSSIS獲利更高或者成本更低，CSSIS是愿意達成合作的。即式(1)可表示為

maxUMG=(CExch-Ccost-zn)。

(24)

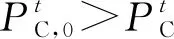
式(11)可表示為

maxUCS=CR+UC-Cpay+zn。

(25)

所以，微電網與CSSIS之間基于納什議價博弈的交互模式可以表述為

(26)

式中U0MG、U0CS分別為非合作博弈模式中微電網和CSSIS的利潤。

通過求解式(26)的均衡解，可以求解出最優納什交易策略，實現第2日利潤的最大化。

為了便于計算，對式(26)取對數，將連乘轉化為求和，目標函數轉化為：

(27)

將系統社會收益ψsw定義為微電網與CSSIS的利潤之和，則系統社會收益最大化模型可表述為

ψsw=UMG+UCS=

Cexch-Ccost+CR+UC-Cpay。

(28)

對式(27)求關于Zn的一階導數可得

(29)

恒等變化化簡可得：

(30)

由式(31)可以看出，納什議價問題實際上也是使系統社會收益最大化問題。

由于CSSIS與微電網交易的相應補償zn在社會收益最大化模型中被抵消，無法確定zn值，有必要引入納什議價理論來分析微電網與CSSIS最優能源交易問題，而不是簡單地利用社會收益最大化模型。由納什定理：在一個有m個博弈方的博弈G={S1,…,Sm：u1,…,um}中，如果m是有限的，且Si|i=1,…,m都是有限集，則該博弈至少存在一個納什均衡，但可能包含混合策略。而根據式(26)可知博弈方為微電網和CSSIS，且交互功率均在限定范圍內，因此存在納什均衡解。

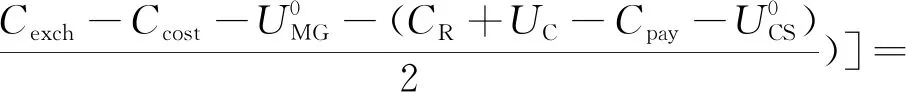
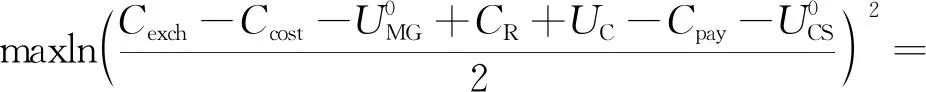
(31)

3 納什議價博弈模型的分布式求解

3.1 求解算法

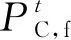
(32)

然后，考慮式(32)中所述的一致性約束，購/售能源達成協議。式(27)可以改寫為

(33)

式(33)具有一致性約束的增廣拉格朗日函數為

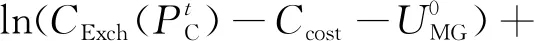
(34)

式中ρk為第k次迭代的罰系數。

由于拉格朗日函數式(27)對于微電網和CSSIS的決策變量是一個可分離函數。利用ADMM分解技術，將問題(27)分解為式(35)和式(36)所示的關于微電網和CSSIS的子問題：

(35)

(36)

式中λk為第k次迭代的拉格朗日乘子。

原問題的ADMM形式表示如下：

maxF1(x)+F2(z)。

(37)

式中F1(x)、F2(z)為微電網、CSSIS的目標函數；x、z為存在耦合的變量，滿足一致性約束：

x=z。

(38)

ADMM迭代求解過程如下，直至滿足式(40)：

(39)

(40)

式中：‖R(k)‖2、‖S(k)‖2分別為原殘差、對偶殘差；εpri、εdual分別為原殘差、對偶殘差的收斂精度。

3.2 求解步驟

納什議價博弈的分布式求解步驟如下：

2)令k=1，迭代開始；

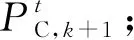
5)基于式(39)更新拉格朗日乘子；

6)為加速ADMM算法收斂，采用文獻[26]中所述罰系數變步長更新公式：

(41)

式中μ、τincr、τdecr為常數。

7)根據式(40)計算殘差，判斷是否滿足收斂條件。若滿足則迭代停止；否則k=k+1，回到式(3)。

4 算例分析

4.1 算例系統

以實際ISMG系統進行信息與能量交互以驗證結論的有效性。實際ISMG系統由微電網和CSSIS組成。其中，上層微電網與電網連接，其組成部分包含WT、PV組成的分布式電源、柴油發電機、燃料電池以及普通負荷；下層CSSIS與微電網連接，由儲能電站以及充換電站組成。

4.2 參數設置

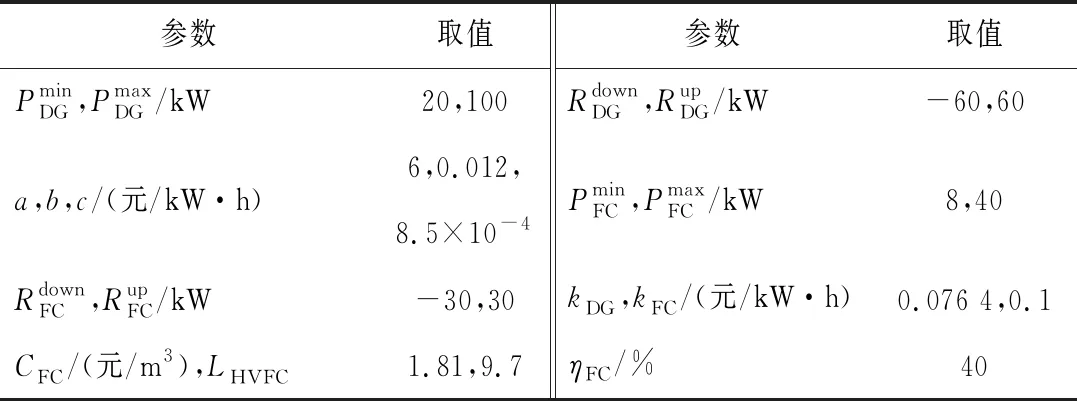
表2 微電網參數

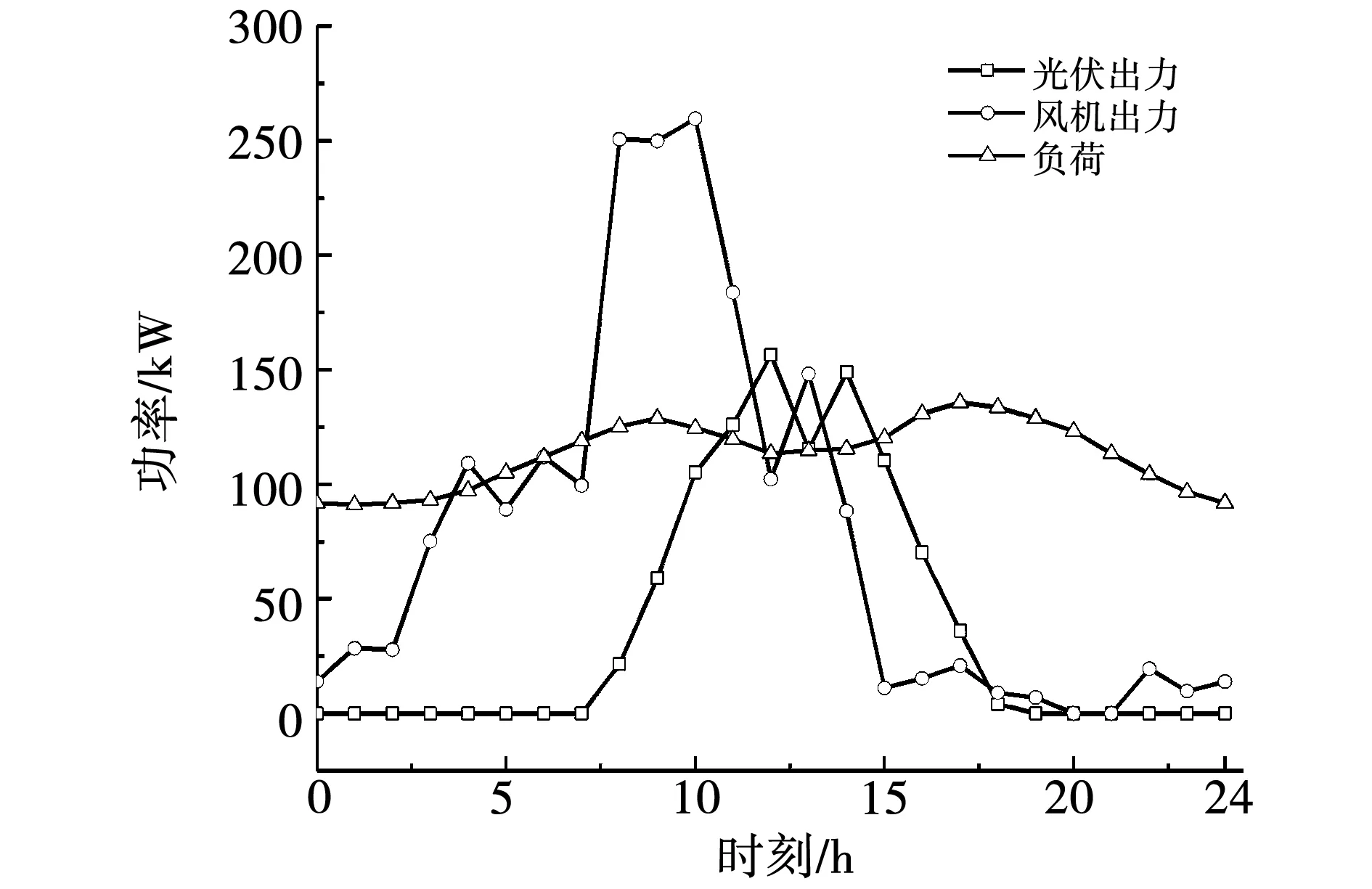
圖2 風機、光伏和負荷的預測出力

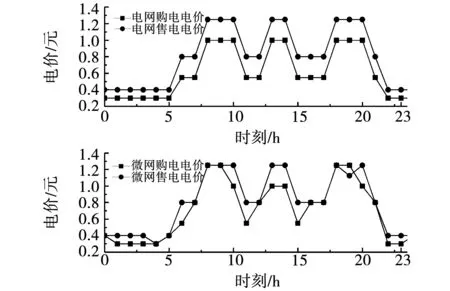
圖3 式(2)涉及的電價信息

4.3 仿真結果及其對比分析

設計2種Case進行對比分析，即：基于納什議價博弈(Case 1)的分布式協調優化調度和基于Stackelberg博弈的雙層協調優化調度(Case 2)，分別就算法收斂性、各利益主體利潤和相關設備出力情況進行分析比較。需要說明的是，Case 2中的博弈模型及求解過程均源自文獻[14]。

4.3.1 算法收斂性

圖4是ADMM算法收斂迭代曲線，可以看出迭代7次上下兩層即可同時達到收斂。隨著迭代的進行微電網利潤逐漸減小，而CSSIS利潤逐漸增大，最終兩者收斂至納什議價解處。圖5是ADMM殘差收斂曲線，由圖可知迭代7次即可達到收斂標準。圖4和圖5表明了ADMM算法具有良好的收斂性，同時也驗證了本模型的可行性。

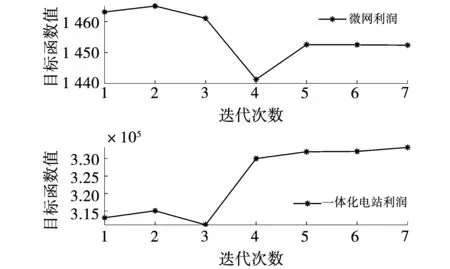
圖4 ADMM算法收斂曲線

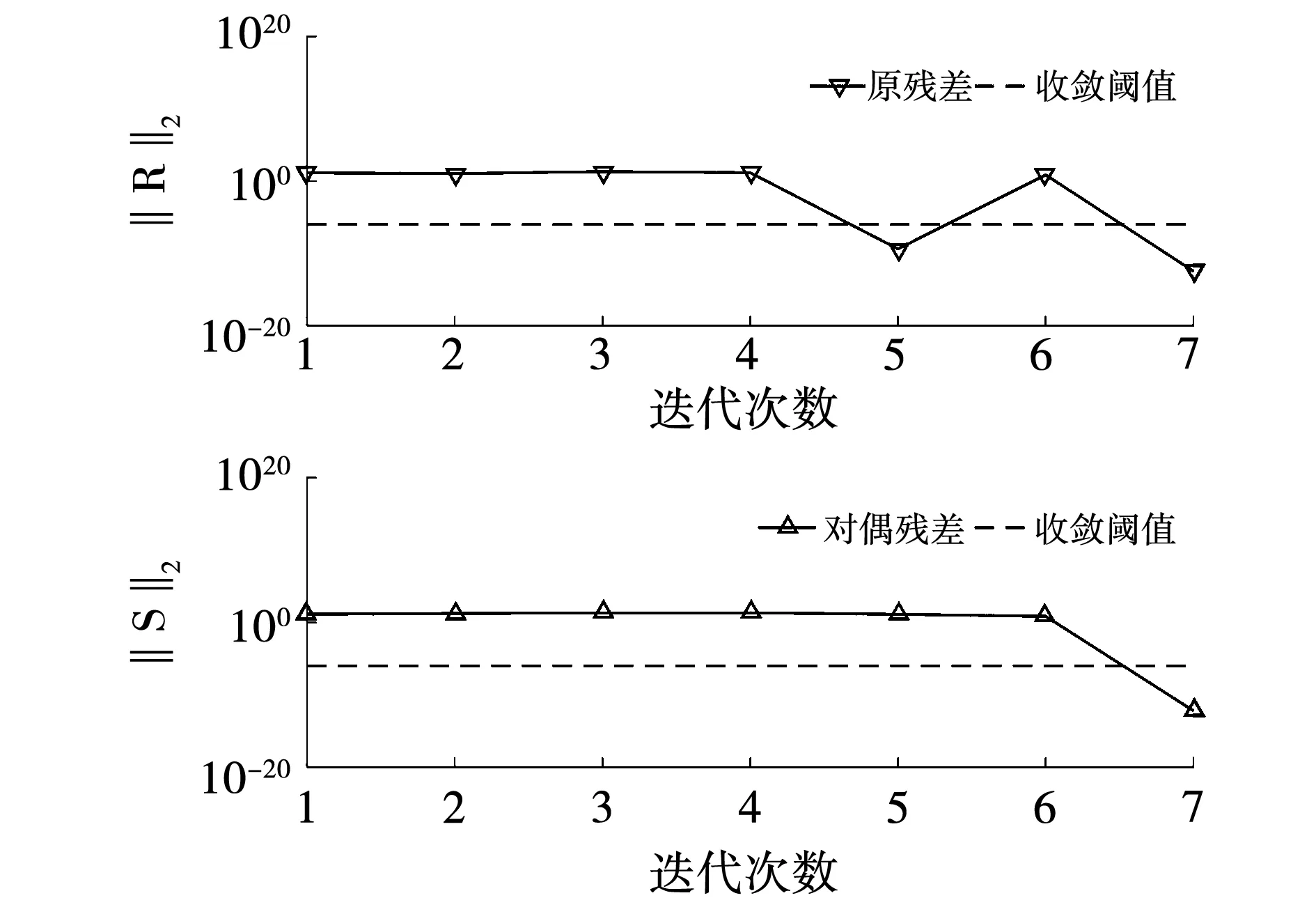
圖5 ADMM殘差收斂曲線

4.3.2 各利益主體的利潤

由表3可知，相比Case 2，Case 1的微電網利潤、CSSIS利潤和系統社會收益分別提高了7.21%、19.03%和18.97%。這充分體現了采用納什議價博弈的經濟性優勢，不僅能同時提高各博弈參與者的經濟效益，而且還能實現更公平、合理的利潤分配，也進一步說明了本模型的有效性。另外，結合表3和公式(30)還可得出納什議價下微電網補償為-26 581.15元。綜合來看，由納什議價理論[30]可知，在此補償下聯盟各參與者可達到帕累托最優，使系統社會收益最大。至于納什議價博弈相比Stackelberg博弈能取得經濟性優勢的原因，將在接下來的設備出力情況部分進行詳細分析和說明。

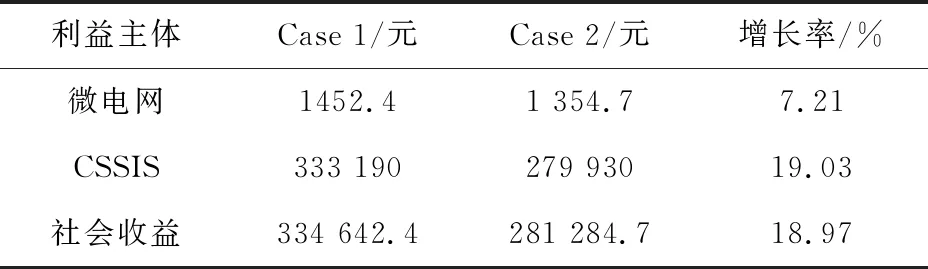
表3 兩種方案下各利益主體利潤對比

4.3.3 微電網及CSSIS出力情況

圖6是2種Case中微電網和CSSIS出力情況，可以看出兩種情況下CSSIS出力趨勢大致相同，但是Case 1中CSSIS出力在大多數時段相比Case 2中都有一定程度的降低。同時可以看出Case 1電網交互功率相較Case 2具有較好的“削峰填谷”效果，時段5-7處于負荷較低，Case 1高于Case 2；時段7-14和時段21-22負荷較高，Case 2一直高于Case 1。即負荷較低時段通過加大與電網交互功率微電網可以獲得更高利潤，CSSIS充電成本也更低；負荷較高時段減小與電網交互功率降低交互成本。這一現象也就能解釋為何納什議價博弈可使微電網和CSSIS利潤以及系統社會收益同時提高，并取得比Stackelberg博弈更多經濟性優勢的原因。

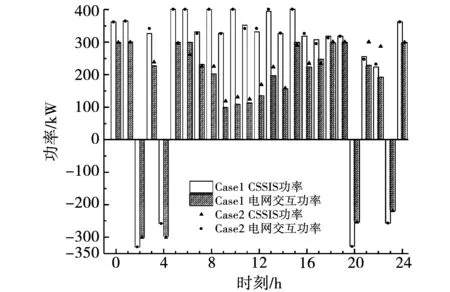
圖6 2種Case中的微電網和CSSIS功率曲線

4.3.4 ESS出力情況

如圖7所示為ESS各時段的出力及SOC值。由圖可知，兩種Case中的SOC值基本都呈現出先升后降的趨勢，但在具體ESS出力情況存在一定區別。具體而言，Case 2中ESS基本都是以極限功率進行充放電，增加了CSSIS的運維及購電成本，而Case 1中ESS的充放電功率調度結果更加靈活，在大部分時刻以相對小功率進行充放電操作或者處于閑置狀態，這在一定程度上減輕了CSSIS的運維成本壓力。這種現象也說明了采用納什議價博弈的調度優勢。即從整個調度過程的角度上來考慮，該方法相比Stackelberg博弈能夠給出更優的調度結果，避免因為不合理的資源調度而帶來的經濟損失。

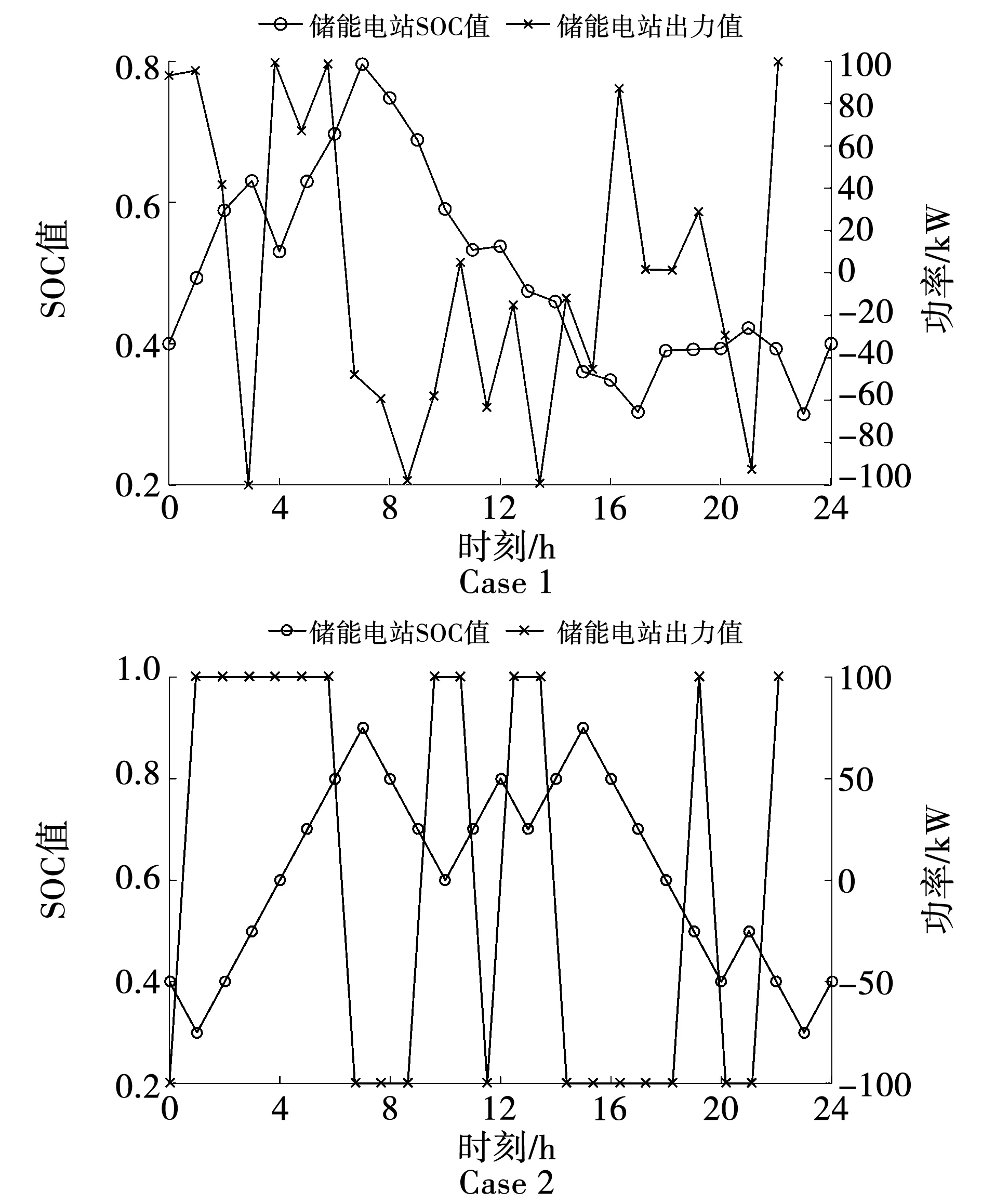
圖7 2種Case中ESS各時段出力及SOC值

4.3.5 FC和DG出力情況

如圖8所示為FC和DG的出力，可見：兩種方案都在PV、WT出力不足時段盡可能以最大功率發電滿足負荷需求，在其出力充足時段盡可能消納能源，DG、FC出力維持在較低水平。可以看出Case 1中DG、FC出力相比Case 2更平滑，主要是由于在時段7-13中，Case 1中DG、FC出力相比Case 2更高。這一時段結合圖2、圖6可知PV、WT出力雖然很高，但仍然無法滿足CSSIS需求。通過增加DG、FC出力不僅可以減少與電網交互功率，降低交互成本，還可以平滑電網交互功率曲線，減少對電網造成的沖擊，這是圖6該時段中電網交互功率下降的原因之一。另外，在時段5-7，Case 1中DG、FC總出力比Case 2小，這是圖6中該時段電網交互功率會上升原因之一。這一現象充分說明了納什議價博弈的優勢，通過促進微電網和CSSIS合作，可更合理調度整個系統內資源，實現兩者互利共贏。

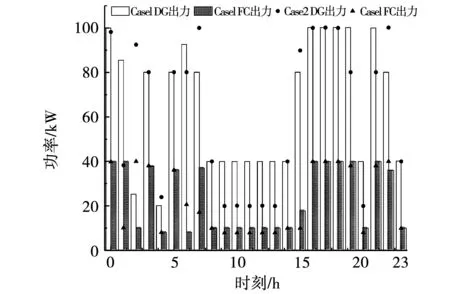
圖8 2種Case中FC、DG出力情況

5 結 論

本文將納什議價博弈運用于不同利益主體的微電網與CSSIS電能交互模型當中，考慮到納什議價模型交互變量存在耦合，利用ADMM算法對其進行解耦，結合商業求解軟件CPLEX對問題進行分布式迭代求解，同時也有效保護了博弈參與方的隱私。最后，結合具體仿真算例對所提出模型以及算法有效性進行了驗證。仿真結果表明：相較非合作博弈模型，本文所提模型通過促進交易雙方達成合作，進一步提升了微電網與CSSIS利潤，更合理調度系統資源，避免因不合理的調度資源帶來的經濟損失，還能實現系統社會收益最大化。對于后續研究可做一定的指導，具體包括：

1)為微電網與CSSIS聯合運行提供借鑒；

2)為后續多充換儲一體化電站微電網運行等研究工作提供分布式計算指導，保障CSSIS和微電網雙方利益與優化計算效率；

3)后續包括進行多微電網與一體化電站存在多方博弈，即多方不同利益主體等研究工作時可供借鑒。

未來將進一步考慮可再生能源以及換電需求不確定性，開展針對含多充換儲一體化電站微電網的分布式優化調度研究工作。