熱傳遞對燃氣輪機突降負載的過渡態性能影響
丁一波, 余又紅, 李鈺潔
(1. 海軍工程大學 艦船動力工程軍隊重點實驗室, 武漢 430033;2. 海軍工程大學 動力工程學院,武漢 430033)
為減少燃氣輪機系統試驗成本,以及研究燃氣輪機控制系統和控制策略,燃氣輪機建立仿真模型具有重要意義。早期的燃氣輪機建模方法大多立足于對其穩態性能的匹配,精度十分有限。然而燃氣輪機實際運行時常常處于復雜多變的動態過程,燃氣輪機內的狀態參數隨著時間變化而不斷發生變化,穩態匹配的研究方法難以滿足對燃氣輪機的精確仿真。因此,為了得到高精度的燃氣輪機仿真模型,對燃氣輪機的動態仿真必不可少。
到目前為止,燃氣輪機的過渡態性能研究已經取得了不少成果,但大部分燃氣輪機模型只考慮了轉子慣性和容積效應。根據研究證明[1-4],除了轉子慣性和容積效應外,熱端固體部件的熱慣性也有著不容忽視的影響。
文獻[5]給出一種用于估算氣流與零部件間熱交換對過渡過程影響的方法,并對某雙軸渦扇發動機的“冷” “熱”兩種加速過程進行仿真計算,結果表明:高溫部件與氣流的熱交換對噴氣發動機的過渡過程有不容忽視的影響,且零部件換熱面積和質量對精度有一定影響但不顯著。屠秋野等[6]在此基礎上,提出了“換熱效應不影響壓氣機、渦輪部件的耗功、做功大小而是影響做功能力”的假設,并考慮了渦輪葉片上的冷卻效果,對雙轉子渦扇發動機的燃氣輪機加速和減速的過渡態性能影響進行研究,結果表明:換熱效應對整機性能的影響主要表現為各部件的響應滯后,而低壓轉子的響應滯后最為明顯;壓氣機的換熱時間常數小于渦輪;在部件中,葉片的換熱時間常數最小,輪轂次之,機匣最大。
對于燃氣輪機而言,除加速、減速的過渡過程之外,還包括負載突變。因此,為進一步研究換熱效應對燃氣輪機過渡態性能的影響,本文建立某三軸燃氣輪機穩態與動態的模型,同時建立傳熱模型,深入研究熱傳遞對燃氣輪機負載突變性能的影響。
1 模型建立
本文以SIMULINK為平臺,采用基于機理的非線性建模方法,采用模塊化建模的思想,基于燃氣輪機轉速平衡、功率平衡、流量平衡建立船用三軸燃氣輪機穩態、動態模型,并在轉子慣性和容積效應的基礎上加入了熱慣性模塊,對突降負載的過渡態進行數值仿真,探究燃氣輪機的動態特性,分析熱傳遞對燃氣輪機動態特性的影響。
1.1 燃氣輪機模型
采用上述模塊化的思想對燃氣輪機進行部件的劃分,如圖1所示,分別建立低壓壓氣機(LC)、高壓壓氣機(HC)、燃燒室(B)、高壓渦輪(HT)、低壓渦輪(LT)、動力渦輪(PT)模塊和轉子慣性環節、容積慣性環節。各模塊均反應了輸入參數與輸出參數之間的關系,模塊與模塊之間通過相關的流動參數連接起來。燃氣輪機性能仿真中須要求解部件特性方程組、參數聯系方程組以及動態環節微分方程組。部件特性方程組表達了部件內的氣動熱力過程,參數聯系方程組則是根據一定的氣路的連接順序計算發動機各部件進出口截面氣流參數,得到有關氣流參數須受共同工作方程的約束。
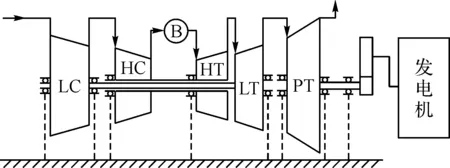
圖1 三軸燃氣輪機示意圖
本文依據文獻[6]提供的方法,建立的燃氣輪機模型如圖2所示:
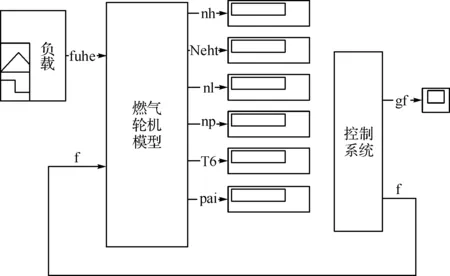
圖2 三軸燃氣輪機仿真模型
1.2 熱傳遞模型
假設燃氣溫度高于金屬溫度,那么從燃氣到金屬的熱傳導率可以用一個一維熱傳導公式來近似[8]:
(1)
式中:q為熱流量;h為對流換熱系數,與氣體物性、換熱表面的幾何性質、氣體流動狀態、表面粗糙度等因素有關;A為換熱面積;Tg、Tm分別為氣體和金屬固體溫度;M、Cm分別為為金屬質量和比熱容;t為時間;下標g、m別表示氣體和固體。
采用過余溫度θ表示:
θ=Tm-Tg
(2)
則公式(1)可以表示為:
(3)
式中:τ為換熱時間常數。
金屬部件的溫度為:
(4)
式中:Tm0為金屬部件初始溫度;t0為開始進行換熱的初始時間。
則得到修正后的出口氣體溫度Tg′可表示為:
(5)
式中:Cg為氣體定壓比熱容;mg為氣體質量流量。
壓氣機和渦輪部件的質量較大,因而有較大的熱慣性,而燃燒室等薄殼結構部件的熱慣性可以忽略。在壓氣機和渦輪部件中沿流道方向的各級幾何尺寸、氣流壓力、溫度以及速度分布都有很大差別,都會影響換熱系數和熱流量。本文對此進行了簡化,采用進出口對流換熱系數的平均值作為熱端部件整體的對流換熱系數,對傳熱模型進行簡化。
本文采用簡化公式(6)計算對流換熱系數:
(6)
式中:Nu為努塞爾數;λ為氣體導熱系數;d為特征長度。
根據文獻[9]使用公式(7)計算Nu:
(7)
式中:Re為雷諾數;Pr為普朗特數。
建立的傳熱模型如圖3所示,并將其加入到搭建好的燃氣輪機的仿真模型中進行計算。
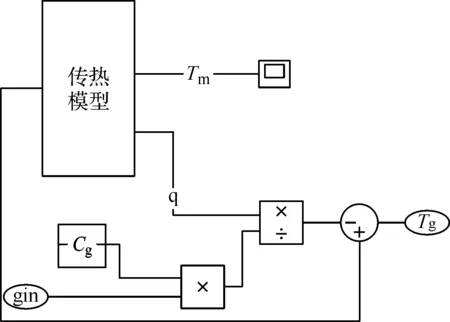
圖3 傳熱模型
2 仿真結果與性能分析
燃氣輪機通過動力渦輪做功帶動負載,其部件性能決定整機性能,故選取動力渦輪作為渦輪部件的代表進行分析。同時轉子系統中高壓渦輪和高壓壓氣機相距最近,且中間經歷燃燒室,其傳熱影響較為明顯,故選取高壓壓氣機作為壓氣機部件的代表進行分析。本文對燃氣輪機進行了120 s數值仿真計算,在50 s時突降負載,以部件溫度、熱流量、出口溫度、功率、轉速為性能分析參數。
根據上一節建立的傳熱數學模型和文獻[10] 可知,熱慣性系統為一階慣性系統,負載突變條件下的燃氣溫度輸入為階躍輸入。如圖4仿真結果所示,熱端部件溫度響應為一階階躍響應,證明了傳熱模型建立的正確性。由于負載突降,導致動力渦輪出口溫度突降,而熱端部件溫度由于存在較大的熱慣性,呈緩慢下降趨勢,使得較長的時間內流體與固體之間存在溫差驅動產生的熱傳遞。
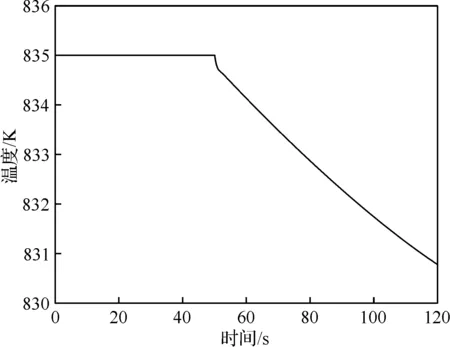
圖4 動力渦輪部件溫度響應
為了進一步量化分析熱傳遞產生的影響,得到如圖5所示的渦輪部件內熱流量變化曲線(負值代表固體向流體傳熱)。50 s之前燃氣輪機處于穩態運行狀態,不存在溫差,熱流量為0。在50 s負載突降時,溫差最大,熱流量最大,達到1 414 kW。隨著燃氣輪機的控制調節作用,系統重新趨向于穩定狀態,傳熱量逐步減小并趨向于0。由分析可以得到,燃氣輪機穩態運行時,熱傳遞對性能不產生影響,各參數都處于穩態,當燃氣輪機工況發生改變,處于進入到新穩態的過渡態之中,熱傳遞在一定時間內產生的影響不可忽略。
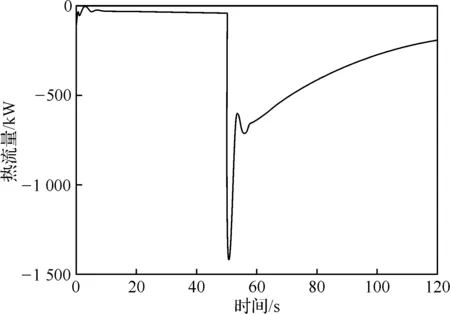
圖5 渦輪部件內熱流量響應
從圖6、圖7可以看出,在溫度波動的50~60 s內以及溫度相對穩定的60~120 s內,換熱模型的高壓壓氣機和動力渦輪出口溫度均高于絕熱模型,這是由于負載突變造成溫差和熱端部件較大的熱慣性對流體加熱的效果,熱傳遞對燃氣輪機過渡態性能的影響不可忽略。
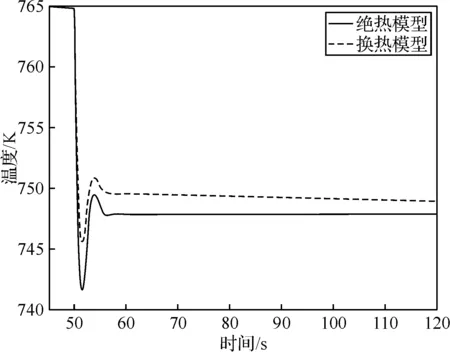
圖6 高壓壓氣機出口溫度響應
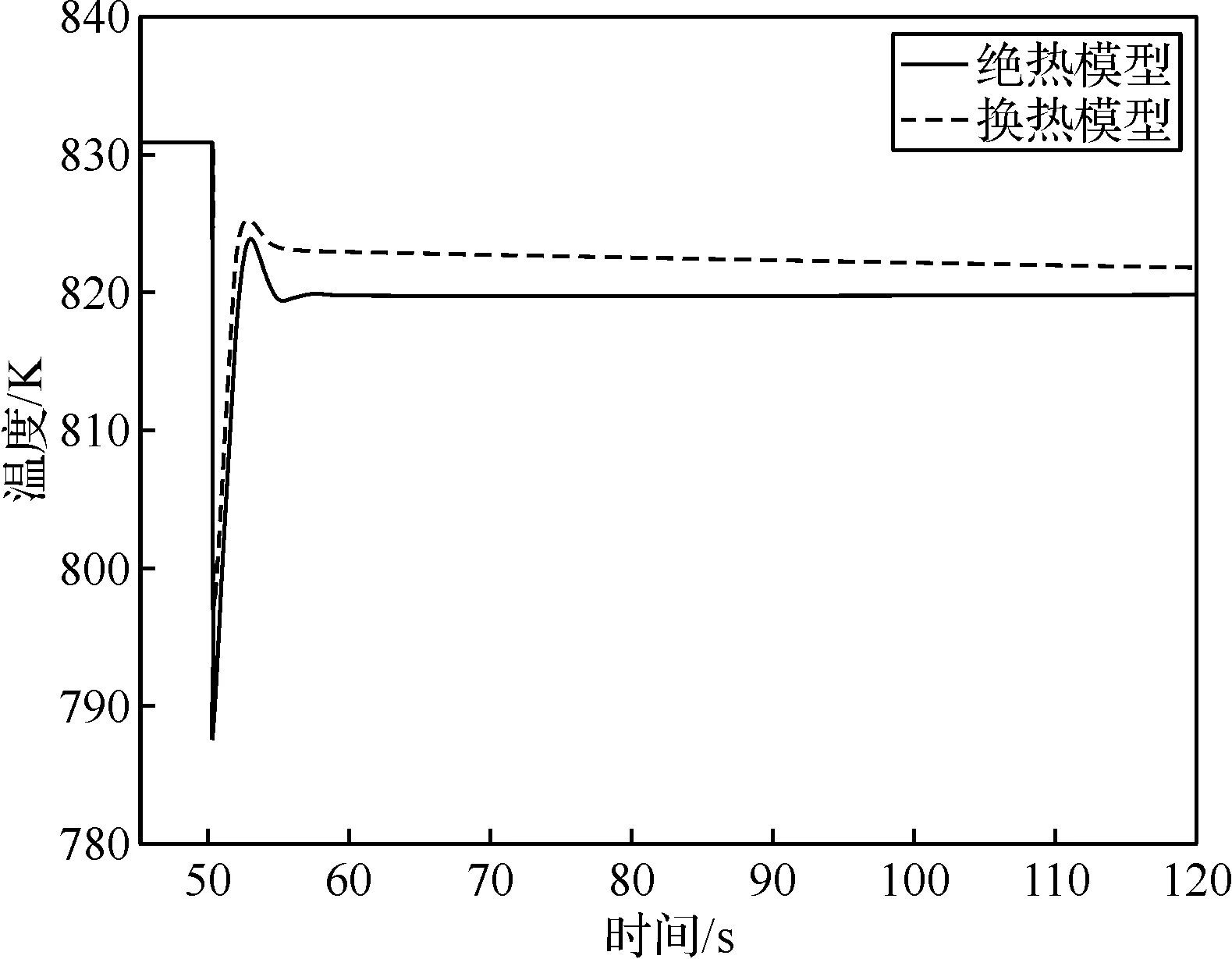
圖7 動力渦輪出口溫度響應
如圖8、圖9所示,60~120 s內,換熱模型和絕熱模型的動力渦輪做功功率相等,換熱模型的壓氣機功率高于絕熱模型。由于加熱使得空氣在壓氣機內被加熱,更難被壓縮,導致壓氣機耗功增大。同時,由圖10可以看出,熱傳遞導致燃氣輪機耗油量增大。這是因為相較于絕熱模型,由于壓氣機耗功增大,且熱損失增加,控制系統為保持渦輪做功功率不變,增大了燃油供給量。
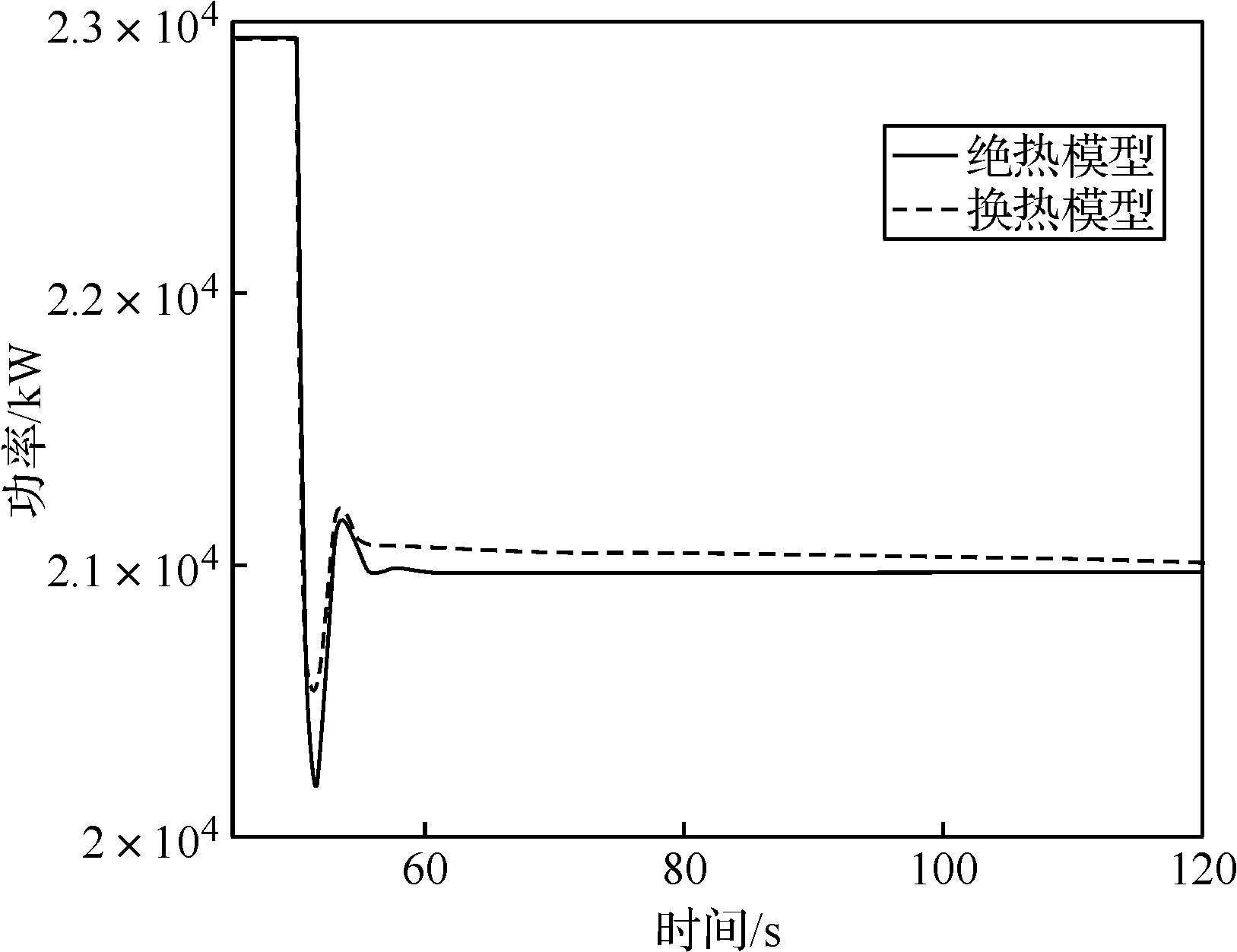
圖8 高壓壓氣機功率響應
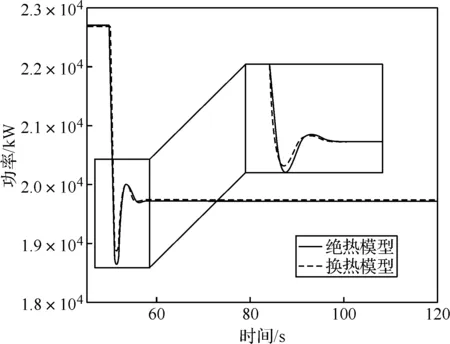
圖9 動力渦輪功率響應
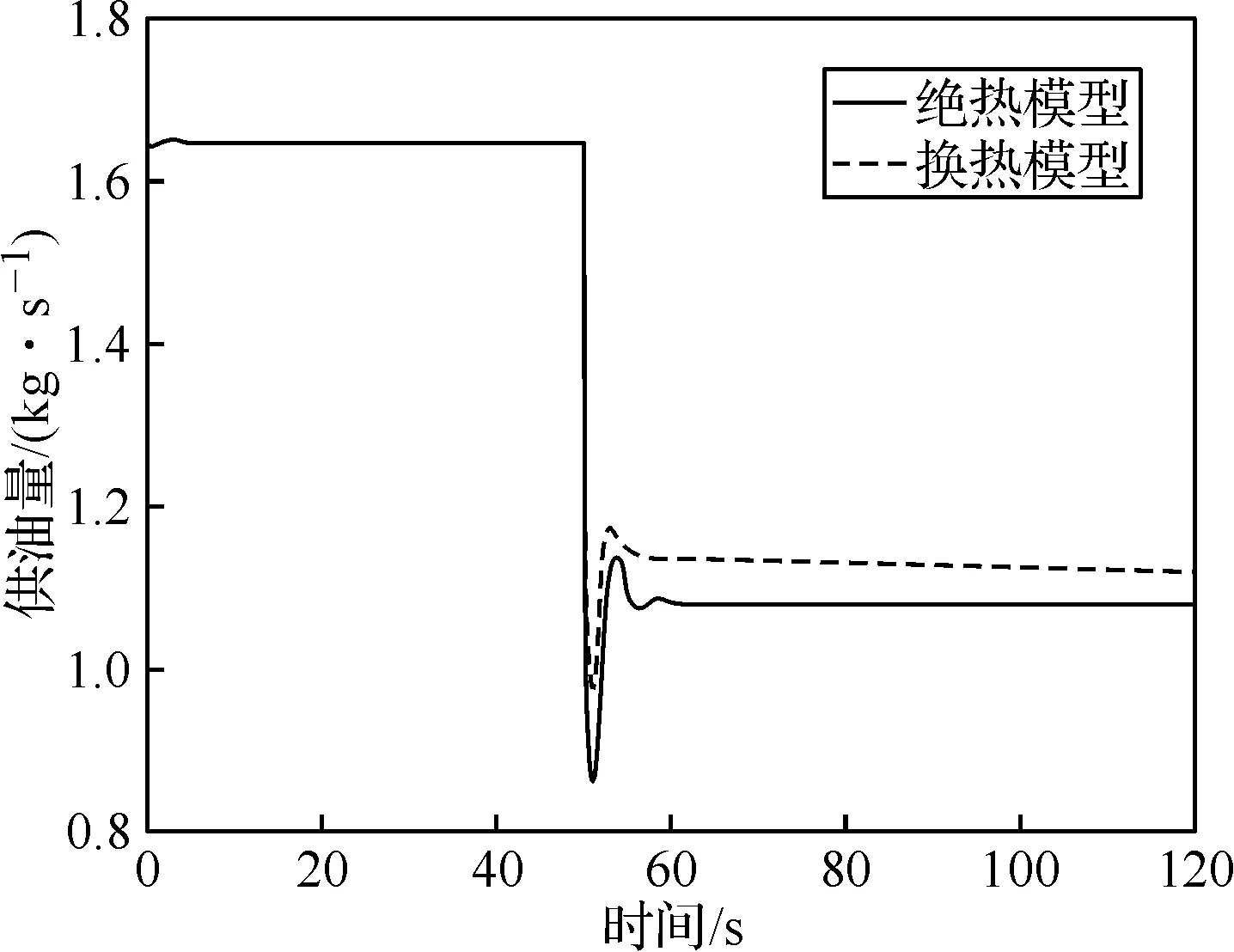
圖10 供油量響應
本模型為發電燃氣輪機,為保證動力渦輪轉速在任何條件下都穩定在3 000 r/min,控制系統需要對轉速進行調節。由圖11可得,換熱模型的動力渦輪轉速超調量小于絕熱模型,換熱模型的超調量降低了40%。除此之外,由圖7至圖11所示,換熱模型各個參數的超調量均低于絕熱模型。因為熱慣性的存在,當溫度下降時,熱端部件源源不斷地加熱,降低了溫降速率;當溫度上升時,熱端部件成為熱阻,降低了溫升的速率,且溫度作為燃氣輪機一個重要的狀態參數,熱傳遞對溫度的影響決定了它必然對燃氣輪機性能產生影響,傳熱降低了溫度的超調量,所帶來的結果就是功率、轉速的變化趨勢同溫度的變化趨勢相同,其超調量均有所降低。
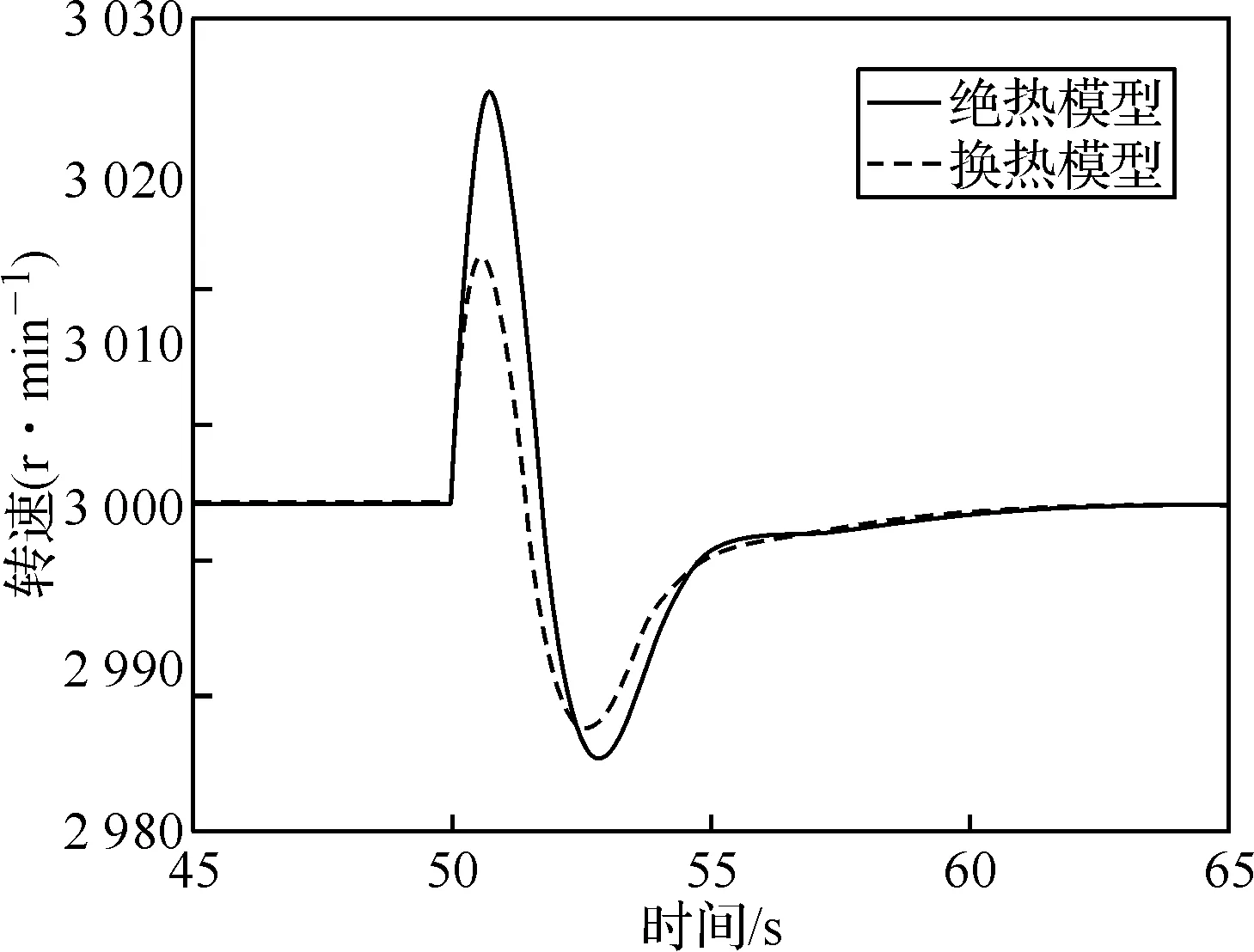
圖11 動力渦輪轉速響應
3 結論
(1) 負載突降的過渡態過程中,流體溫度響應屬于階躍響應,熱端部件溫度響應屬于一階系統響應,其變化速率的不同是帶來溫差的根本原因。
(2) 燃氣輪機穩定運行時,熱傳遞對穩態性能不產生影響,當燃氣輪機處于過渡態之中,熱傳遞在一定時間內產生的影響不可忽略。
(3) 熱傳遞導致壓氣機耗功增大,熱損失增加,控制系統為保持渦輪做功功率不變,增大了燃油供給量。
(4) 溫度作為燃氣輪機一個重要的狀態參數,熱傳遞對溫度的影響決定了它必然對燃氣輪機性能產生影響,熱傳遞降低了溫度的超調量從而降低燃氣輪機其他性能參數在控制階段的超調量。

