絲網芯內鈉薄液膜蒸發與毛細特性研究

馬譽高，張英楠，余紅星，黃善仿,*

(1.清華大學 工程物理系，北京 100084；2.中國核動力研究設計院 核反應堆系統設計技術重點實驗室，四川 成都 610041)

堿金屬熱管是一種利用毛細力驅動的高效非能動傳熱元件，主要應用于核能、航空航天等領域[1-4]。由于特種用途對于幾何尺寸和重量的嚴格限制，堿金屬熱管管徑通常較小(小于20 mm)，在該尺寸下一般采用金屬絲網芯結構。絲網芯提供的毛細力是熱管內工質自然循環的最終動力來源。

毛細力由絲網內的液膜形態決定，而液膜形態受絲網幾何構型及工質與絲網的潤濕特性影響。其中，絲網芯的幾何構型由絲徑、孔徑等參數決定，工質與絲網的潤濕特性受絲網與工質間分子作用力、界面形態、粗糙度和運行溫度等因素影響。

在理論方面，已有大量學者針對毛細孔內蒸發薄液膜的傳熱傳質過程開展了研究，其難點在于液膜與固體接觸線的微觀形態描述。當前的主流理論認為，在宏觀的三相接觸點處吸附有納米級厚度的前驅膜。前驅膜理論解決了三相點直接相交帶來的應力奇異性問題(Huh-Scriven佯謬[5])，該理論已在實驗上得到了證實[6-11]。1976年，Wayner等[12]基于前驅膜理論，提出了相變傳熱中接觸線上的吸附和毛細管冷凝模型，并系統性地建立了一維液膜傳熱傳質本構方程。Wayner將液膜分為3個區域，包括平衡液膜區、蒸發薄液膜區和本征液膜區。在平衡液膜區，存在納米級厚度的靜止液膜；在蒸發薄液膜區，液膜開始流動導熱，并在氣液界面發生相變，液膜厚度上升，液膜受分離壓力和毛細力的共同作用；在本征液膜區，液膜的曲率趨于定值，液膜主要受毛細力的作用。Wang等[13-14]、寇志海[15]、金鑫[16]以及Hanchak等[17]基于Wayner模型進行了進一步研究，針對非極性工質，發展了一維毛細孔蒸發彎月面液膜理論，對氨、甲醇、戊烷和正辛烷等非極性工質進行了分析，考慮過熱度、孔徑、蒸發冷凝系數和固液界面滑移等因素對液膜的傳熱傳質和潤濕特性的影響，對初始液膜厚度進行了敏感性研究。在這一階段的研究中，由于非極性工質熱導率低(一般低于絲網芯材料2個數量級)，傳熱過程通常簡化為一維導熱模型。Tipton等[18-19]在Wayner理論的基礎上，進一步考慮了分離壓力的電子分量(電場力)，對圓柱孔內的鈉液膜進行了計算。分析表明，在液態金屬薄膜的傳熱傳質與潤濕過程中，電場力的作用不可忽略。

為進一步研究堿金屬工質在絲網芯中的毛細和浸潤特性，本文以前驅膜理論和蒸發液膜理論為基礎，考慮鈉工質的高導熱率特性與絲網芯的圓柱幾何結構，基于廣義Young-Laplace方程、Hertz-Knudsen-Schrage方程、Kelvin方程和穩態導熱方程，建立液態鈉在絲網芯內的蒸發薄液膜傳熱傳質與鋪展模型，對液態鈉工質在絲網芯表面的浸潤現象和毛細現象進行分析，并探究不同運行參數對鈉液膜傳熱傳質與毛細特性的影響。

1 模型與方法

本文基于前驅膜理論和蒸發液膜理論建立微觀液膜模型。計算模型包括廣義Young-Laplace方程、Hertz-Knudsen-Schrage方程、Kelvin方程和穩態傳熱方程。

在對純液態金屬工質分析中，考慮其分子特性對分離壓力的影響，以及高熱導率對液膜和壁面橫向傳熱的影響。同時考慮絲網芯幾何形狀對液膜分布的影響，在一維平板模型的基礎上建立一維圓柱模型。使用Bond數(Bo)衡量重力與表面張力的相對效應：

Bo=ρgL2/σ

(1)

其中：ρ為液相密度；g為重力加速度；L為特征尺寸，取絲網孔徑；σ為表面張力。

當絲網孔徑達到100 μm以下時，Bo降低至10-3量級，此時表面張力σ遠大于重力，因此忽略絲網內液膜所受重力。本文采用的基本假設為：1)工質和壁面熱物性參數為常數；2)氣相工質為飽和蒸汽；3)液相工質的流動狀態為不隨時間變化、不可壓縮層流流動；4)忽略熱毛細力對傳熱傳質的影響以及馬蘭戈尼對流效應。

1.1 壓力控制方程

毛細蒸發薄液膜模型需要首先建立氣液界面兩側的壓強關系。Young和Laplace在1805年提出了Young-Laplace方程，認為氣液界面兩側的壓強差為毛細壓強[5]。隨著研究的深入，廣義Young-Laplace方程考慮了分離壓強，認為氣液界面兩側的壓強差是由毛細壓強pc和分離壓強pd共同決定的：

pv-pl=pc+pd=pc+pd,vdw-pd,ele

(2)

式中：pv為氣相壓強；pl為液相壓強；pd,vdw為范德華分量；pd,ele為電子分量。式(2)表明，在常物性的假設下，毛細壓強pc和分離壓強pd只與液膜厚度的0～2階導數有關。對于液態鈉工質，毛細壓強pc與氣液界面的曲率有關；分離壓強pd與液膜的厚度有關，包括范德華分量pd,vdw和電子分量pd,ele。

對于任意的氣液界面，毛細壓強pc的表達式為：

pc=σ(K1+K2)

(3)

其中，K1和K2為曲面上任意兩個互相垂直平面的曲率，兩個曲率之和為定值[20]。在不同的曲面和維度下，曲率的取值也不完全相同。如在毛細管中，毛細管半徑為r，若假設曲面為球面，則K1=K2=cosθ0/r；若曲面不為球面，則K1=δ′/(1+δ2)1.5、K2=δ/(r-δ)(1+δ2)0.5，其中δ1為液膜厚度。在一維模型下，K1=K=δ′/(1+δ2)1.5、K2=0。

在一維模型下，分離壓強的范德華分量和電子分量具體表達式為：

(4)

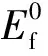
1.2 蒸發質量通量

在液膜中所傳導的熱量，除少部分用于提供工質在流動中升溫所需的焓變，絕大部分用于工質在氣液界面發生蒸發相變。計算氣液界面上凈蒸發質量通量最常用的方程為Hertz-Knudsen-Schrage方程[15]：

(5)

其中：m″為蒸發質量通量；α為蒸發冷凝概率；M為液相原子質量；Rg為氣體常數；p為壓強；T為溫度，下標v表示氣體，lv表示氣液交界面；pv_equ為氣液界面平衡蒸汽壓；psat為氣相飽和壓強。

若氣液界面存在曲率，且滿足薄液膜的假設，則毛細壓強和分離壓強對氣液界面平衡蒸汽壓的影響不可忽略。基于Kelvin方程對氣液界面平衡蒸汽壓進行修正[5]：

(6)

其中氣相飽和壓強可通過相應的熱物性方程進行計算。可見，當毛細壓強與分離壓強之和越大，越傾向于使液膜脫離壁面時，對工質蒸發的抑制程度越強；反之，則促進工質的蒸發。若已知參考溫度和相應的參考飽和壓，當氣液界面溫度與參考溫度差異較小時，也可通過Clausius-Clapeyron方程[5]計算：

pv_equ(Tlv)=psat_ref(Tsat_ref)·

(7)

蒸發質量通量不僅與毛細壓強和分離壓強有關，同時也與液相壓強的1階導數有關。基于不可壓縮層流流動的假設，同時假設固液界面無滑移、氣液界面無剪切力，液相壓強與蒸發質量通量可通過如下表達式計算：

(8)

其中：ν為液體黏度；θ為接觸角。

對式(8)求導，可得到：

(9)

基于上述分析，式(2)～(9)在液相壓強、毛細壓強和分離壓強與蒸發質量通量之間建立了聯系，從而實現液膜潤濕特性與傳熱傳質的耦合計算。

1.3 傳熱模型

在對水和有機物等非極性工質進行薄液膜分析計算時，往往將壁面邊界假設為定壁溫邊界條件，不考慮橫向傳熱[14]。這是因為與金屬材質的壁面相比，水和有機物等非極性工質的熱導率非常小，熱量幾乎全部通過壁面傳導，壁面溫度的變化在計算中可忽略，因此定壁溫的假設合理。但對于液態堿金屬工質，液膜熱導率與壁面熱導率相當，甚至高于壁面熱導率。在這一工況下，液膜和壁面的橫向傳熱不能忽略，溫度梯度的主方向為計算方向，定壁溫邊界條件也不再適用，需要建立新的傳熱方程。

忽略厚度方向上的溫度梯度，則在xi處，壁面和液膜的溫度均為定值，即：

(10)

本文模型中，不同的傳熱路徑對應不同的熱阻，從而建立工質液膜的熱傳導模型。

1.4 接觸角

在絲網芯熱管中，影響絲網芯抽吸能力的一個重要指標是接觸角。確定不同工況下接觸角的大小、分析接觸角的影響因素，是微觀液膜模型實現的主要任務之一。趙亞博[5]提出了兩種計算接觸角θ0的方法，第1種為微觀方法，設分離壓強pd的不定積分為Π，即Π′=pd，通過修正的Frumkin-Derjaguin方程計算接觸角：

(11)

第2種為宏觀方法，即選取蒸發液膜區和本征彎月面交界處位置的斜率作為接觸角。

這兩種方法均存在一定缺陷，微觀方法的缺陷在于難以確定合適的平衡液膜厚度以及在平衡液膜厚度下液膜所受到的力的種類和具體表達式；而在宏觀方法中，對于判別液膜進入本征彎月面的標準尚未統一，通過主觀判斷會引入較大的不確定性。

因此，本文提出了第3種計算接觸角的方法，即假設在距離平衡液膜區足夠遠的位置，氣液界面曲率為定值，沿圓弧對氣液界面進行延伸，直至與壁面相交，認為氣液界面與壁面在這一點的夾角為接觸角。若二者相切或相離，則認為接觸角為0。

2 模型驗證

本文對微觀液膜模型進行校核。Hanchak等[17]使用顯微反射法測量了正辛烷蒸發薄液膜在毛細孔內的液膜厚度變化，測量精度為±1 nm。實驗中，正辛烷為非極性有機工質，因此分離壓力只需考慮范德華分量；其熱導率較小，不考慮橫向傳熱，采用定壁溫模型。正辛烷工質的物性參數列于表1，通過式(7)計算氣液界面溫度的飽和壓強。

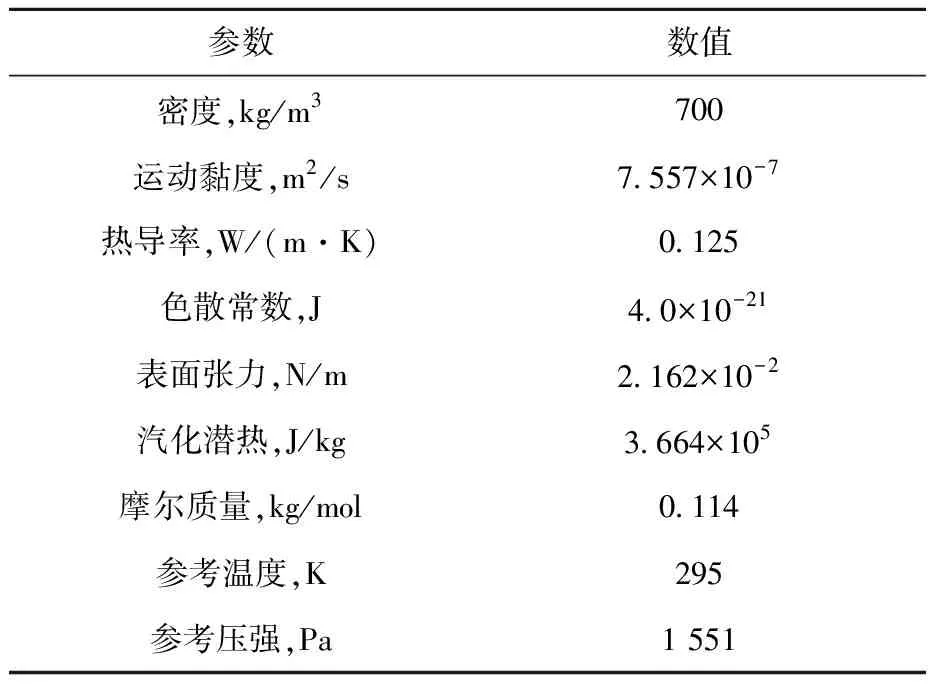
表1 正辛烷工質物性參數

利用微觀液膜模型計算不同工況時所使用的運行參數列于表2，其中蒸發冷凝系數、運行溫度和過熱度均與Hanchak等[15]的結果保持一致。不同工況下微觀液膜模型計算結果與實驗案例的液膜厚度分布示于圖1，實驗誤差棒高度為±10 nm。在微觀液膜模型中，固定初始液膜厚度為20 nm，通過調節初始液膜厚度2階導數，得到不同的液膜厚度分布。Hanchak等也對實驗結果進行了數值模擬，其模擬結果與實驗比對的最大誤差為35 nm，平均誤差在10 nm以內。本文所構建的微觀液膜模型最大誤差為35 nm，平均誤差在10 nm左右，基本達到相同水平，驗證了本文模型的穩定性與準確性。

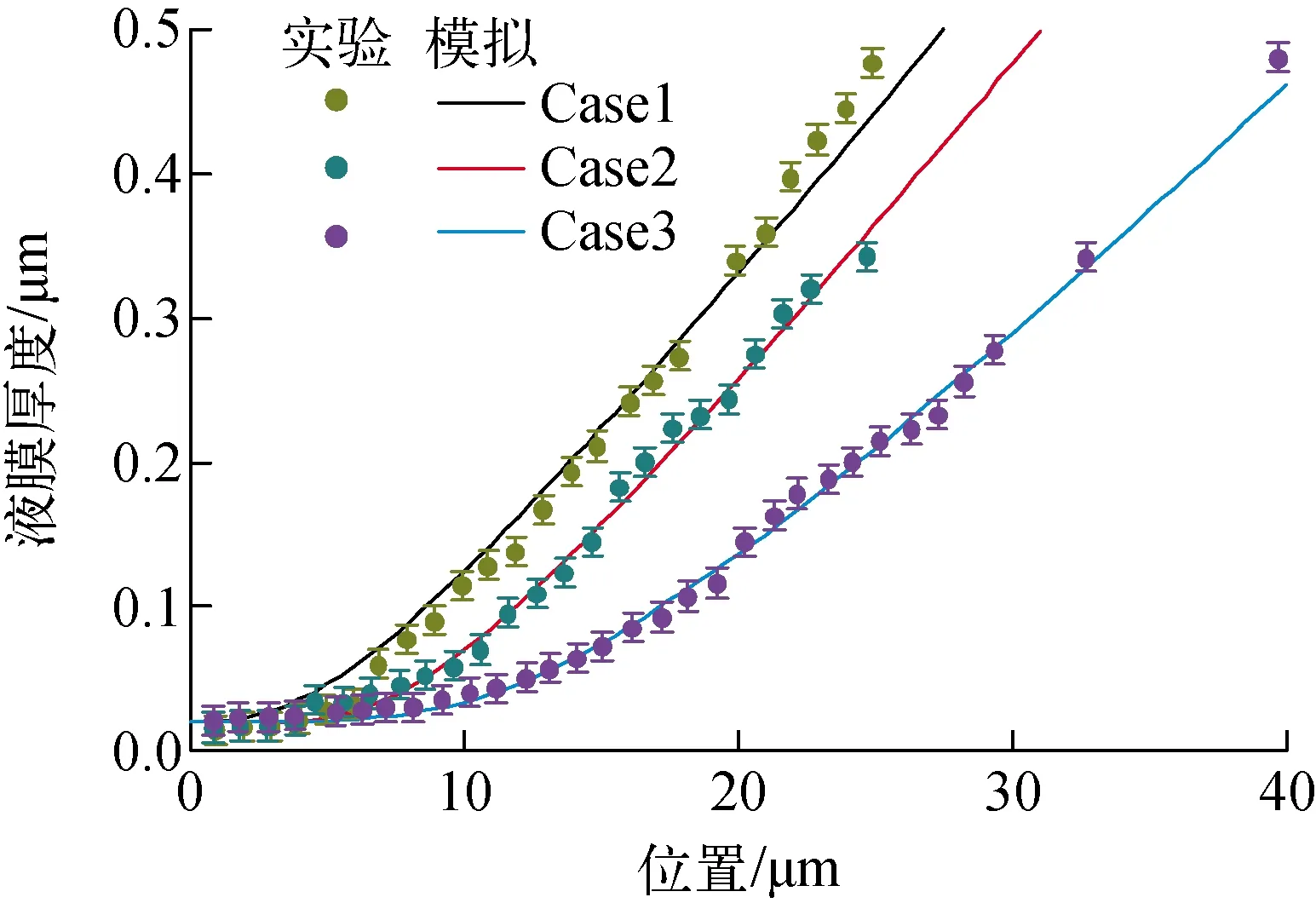
圖1 正辛烷工質微觀液膜模型與實驗案例液膜厚度分布對比

表2 正辛烷工質運行參數

在模型層面，液態鈉和正辛烷的差異性主要體現在工質熱物性和分子作用力種類上，但控制方程的形式并未改變。

3 蒸發薄液膜參數敏感性分析

本文將對影響液態鈉薄膜的傳熱傳質與潤濕特性的運行參數進行逐個分析，包括運行溫度、過熱度、蒸發冷凝系數、絲網芯尺寸和液膜位置。其中過熱度的定義為三相接觸線處液膜溫度和運行溫度(即氣相溫度)的差值。本文的敏感性分析將基于基準運行參數(表3)展開。

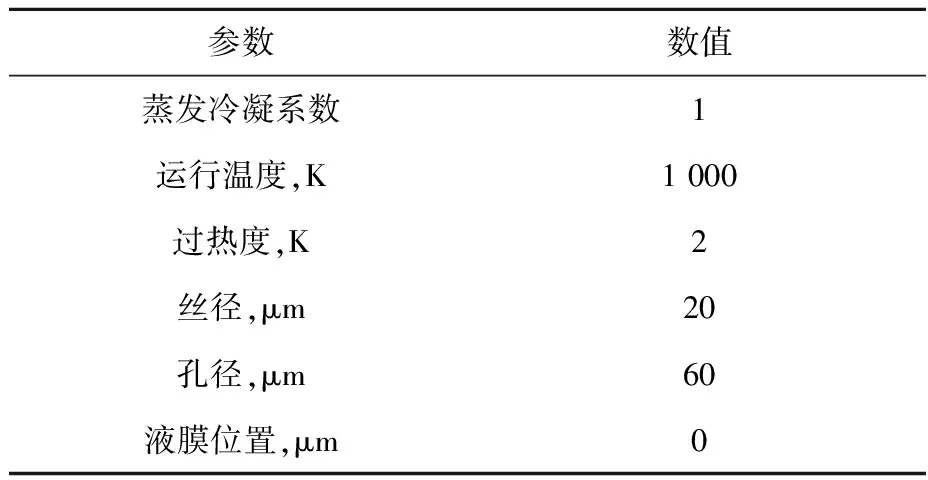
表3 基準運行參數

3.1 運行溫度、過熱度和蒸發冷凝系數的影響規律

首先在一維平板模型下，對運行溫度、過熱度和蒸發冷凝系數進行分析。在其他學者[13-17]的研究中，這3個參數已被廣泛分析，結論也較統一，且普遍適用于目前已知工質。在不同運行溫度、過熱度和蒸發冷凝系數的工況下，計算得到的熱流總量列于表4，液膜厚度和蒸發質量通量分布示于圖2。可見，在不同運行溫度、過熱度和蒸發冷凝系數下，液膜厚度分布趨勢基本一致；蒸發質量通量分布趨勢相似，但數值相差較大。計算的運行溫度區間為800～1 200 K，接觸角從7.5°上升至9.5°，熱流總量從10 W/m上升至2 090 W/m；過熱度區間為0.1～10 K，接觸角從7.5°上升至9.0°，熱流總量從7.5 W/m上升至805 W/m；蒸發冷凝系數區間為0.001～1，接觸角從7.5°上升至8.0°，熱流總量從0.05 W/m上升至155 W/m。

表4 不同運行溫度、過熱度、蒸發冷凝系數工況下的熱流總量

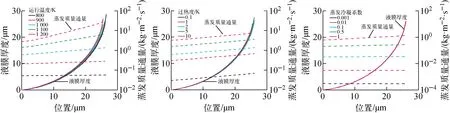
圖2 運行溫度、過熱度和蒸發冷凝系數對液膜厚度和蒸發質量通量分布的影響

綜上，運行溫度、過熱度和蒸發冷凝系數對接觸角基本無影響，對熱流總量有量級上的影響，即運行溫度越高，熱流總量越高；過熱度越大，熱流總量越高；蒸發冷凝系數越大，熱流總量越高。這一結論也可從液態鈉工質的熱物性[23]及式(6)中得到體現。

3.2 絲徑、孔徑和液膜位置的影響規律

對上述一維平板模型參數分析的結論同樣適用于一維圓柱模型。在一維圓柱模型中，除絲徑和孔徑外，液膜位置(即三相接觸點在弧上的位置，液膜位置減小代表液膜后退)也會對計算結果產生影響，這在一維平板模型中無法考慮。如在一維平板模型下，曲率半徑R和孔徑Rc、接觸角θ0的關系為：

R=Rc/cosθ0

(12)

而在一維圓柱模型下，還要考慮水平傾角φ和絲徑Rw，如圖3a所示。

(13)

可見，曲率半徑很大程度上取決于液膜位置。對于簡單方形毛細孔模型，其俯視圖是密接正方形。假設三相接觸線的高度相同，且曲率半徑R1=R2=R，則單孔毛細力F的表達式為：

(14)

液膜在絲網內后退的過程如圖3b所示。可見，在液膜后退的過程中，氣液界面在計算方向上的投影面積先下降后上升，曲率半徑變化趨勢與具體的接觸角和水平傾角有關。當水平傾角大于90°時，液相工質力學平衡穩定性差，液膜難以在這一幾何下維持穩定。400目不銹鋼絲網下單孔毛細力隨接觸角和豎直角(豎直角為水平傾角與接觸角之和，反映三相接觸點在圓柱截面上的位置)的變化示于圖4，運行參數與基準工況參數相同。圖4中，實線位置的水平傾角小于90°，液膜穩定性較好，接觸角越大，毛細力越大；虛線位置的水平傾角大于90°，液膜穩定性較差，接觸角越大，毛細力越小。可見，在不同的接觸角下，隨著豎直角的增加，毛細力均出現先上升后下降的變化趨勢，且接觸角越大，極值點出現的豎直角越大，數值也越大。如果只考慮水平傾角小于90°的工況，則當接觸角相同時，毛細力隨著豎直角單調上升。從前文分析可知：在運行溫度較高的工況下，液態鈉工質的潤濕性較好，接觸角較小，因此毛細力隨液膜接觸線位置的變化存在拐點。因此在一定范圍內，液膜在絲網內回退將提升毛細力，但當液膜進一步在絲網芯內部回退時，便有可能發生液膜接觸線位置下降同時毛細力下降的正反饋現象，導致局部干涸。

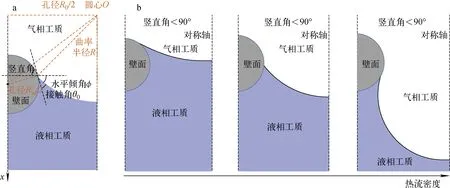
圖3 一維圓柱模型(a)和液膜后退過程(b)示意圖

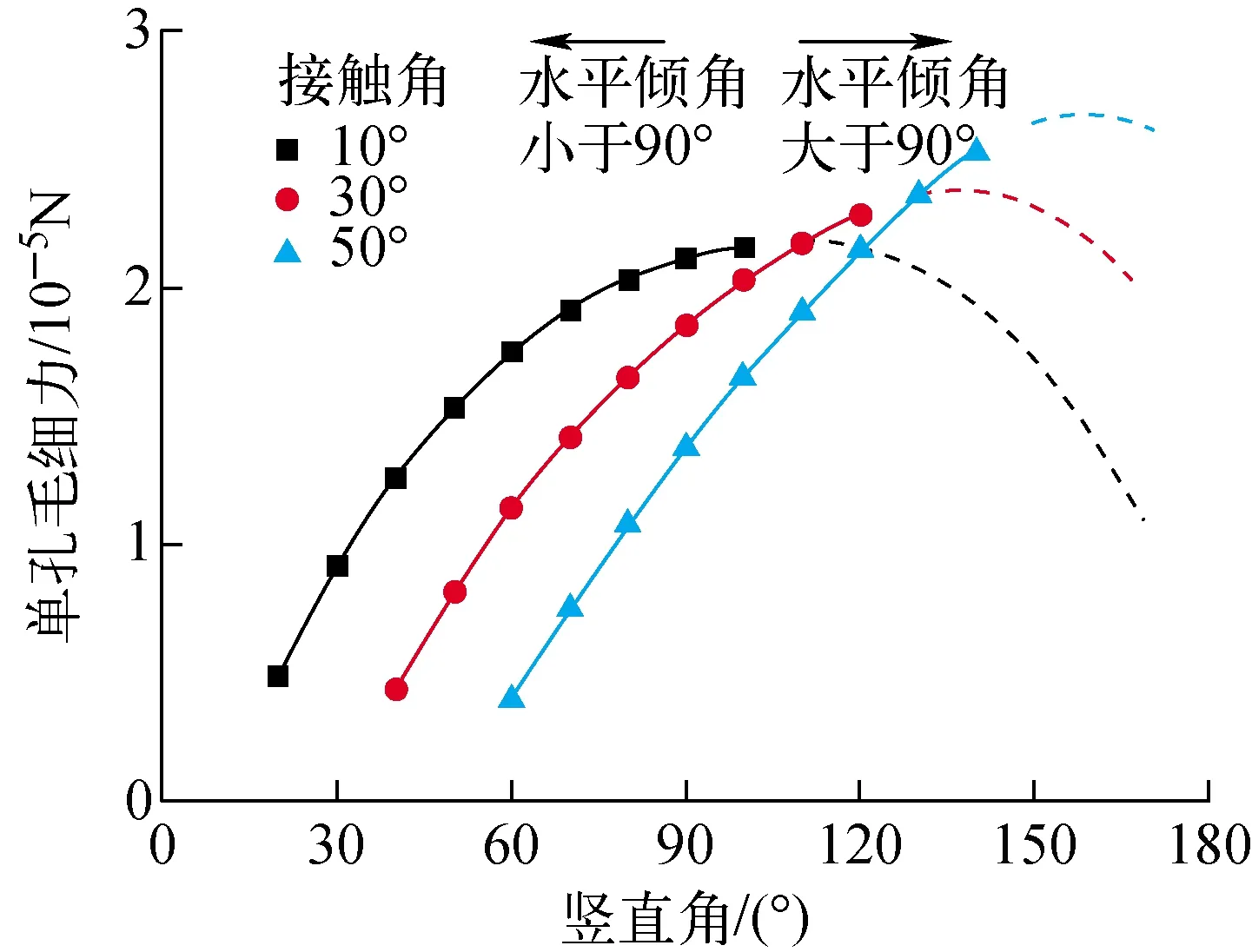
圖4 單孔毛細力分布

不同絲徑、孔徑和液膜位置下計算得到的熱流總量列于表5。可見，這些參數對液膜厚度分布和蒸發質量通量分布產生了影響。絲徑區間為10～50 μm，熱流總量從120 W/m下降至15 W/m；孔徑區間為40～80 μm，熱流總量從35 W/m上升至175 W/m；液膜位置區間為3～-1 μm，熱流總量從65 W/m上升至225 W/m。

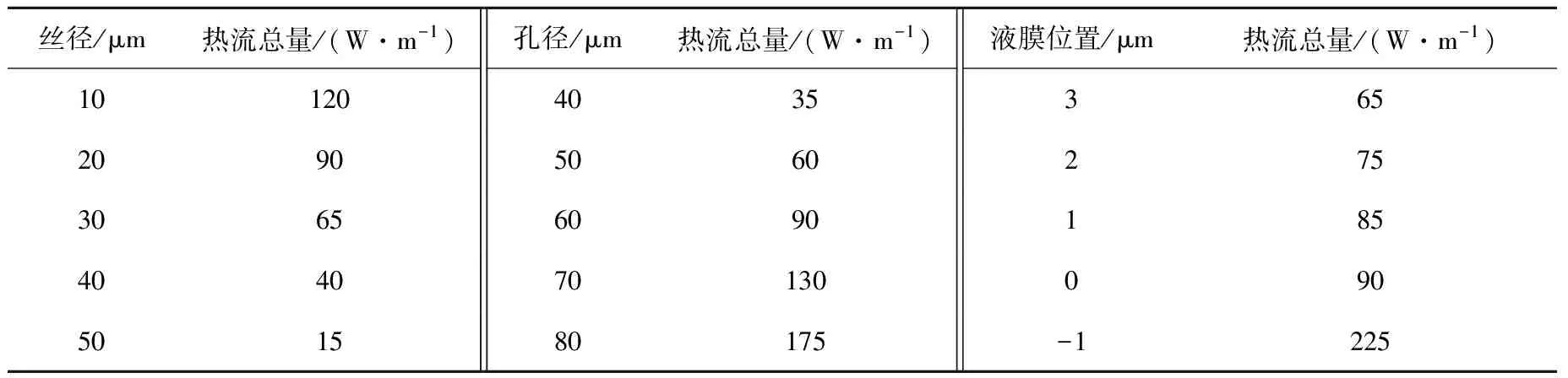
表5 絲網芯尺寸工況

對于不同的絲徑和孔徑，從孔隙率角度考慮，孔隙率越大，氣液界面的面積越大，從而影響蒸發質量通量分布和熱流總量。因此，絲徑越大，熱流總量越低；孔徑越大，熱流總量越高；液膜越后退，熱流總量越高。不同絲徑、孔徑和液膜位置下的液膜厚度和蒸發質量通量分布示于圖5。在其他條件不變的前提下，液膜朝著絲網芯內部后退，接觸角上升的同時，傳熱面積增大，傳熱傳質能力上升，毛細孔能提供的毛細力先上升后下降。因此在輸入熱流的一定變化范圍內，液膜能通過調整自身的位置，在一定范圍內契合絲網芯所需的蒸發量和力學平衡，體現了液膜的動態調整能力。但動態調整能力存在范圍，而范圍的大小取決于工質種類與絲網芯尺寸。

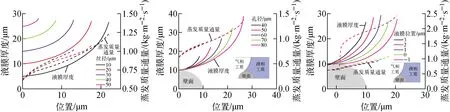
圖5 絲網芯尺寸對液膜厚度和蒸發質量通量分布的影響

4 結論

本文基于前驅膜理論和蒸發液膜理論建立了微觀液膜模型。通過對運行參數進行敏感性分析，研究了各參數對液膜傳熱傳質與潤濕特性的影響。運行溫度、過熱度和蒸發冷凝系數對接觸角基本沒有影響，但對熱流總量有量級上的影響。運行溫度越高，熱流總量越高；過熱度越大，熱流總量越高；蒸發冷凝系數越大，熱流總量越高。絲徑越大，熱流總量越低；孔徑越大，熱流總量越高。

液膜接觸線位置與絲網芯的動態調整能力有關。在液膜在絲網內回退的過程中，毛細力呈先上升后下降的變化趨勢。因此在一定熱流范圍內，液膜在絲網內回退將提升毛細力，從而具有動態調整能力，隨輸入熱流的變化來改變液膜接觸線位置，能自動適應所需的蒸發量和力學平衡。但由于毛細力隨液膜接觸線位置的變化存在拐點，因此在熱流較高的工況下，有可能發生液膜接觸線位置下降的同時毛細力下降的正反饋現象，導致液膜脫離絲網芯，并發生干涸。

值得指出的是，文獻中堿金屬薄液膜蒸發實驗研究稀缺，因此本文模型采用正辛烷蒸發薄液膜實驗結果進行了初步驗證。后續將開展液態鈉液膜相關的實驗研究，結合理論模型進一步探索由于工質變化帶來的特殊現象。