多元線性回歸模型的異方差問題的淺析
尚云艷 祝師強 孫浩


摘 要:“應用回歸分析”課程是高校應用統計學專業均開設的專業核心課程,多元線性回歸模型是非常重要的知識內容,但是由于其理論內容復雜,學生學習難度大,針對此問題,本文從權的概念出發,利用權倒數的性質論證了加權線性回歸的合理性。并以北京市15個經濟開發區的銷售收入數據為例,運用加權最小二乘估計方法改進模型,最后從殘差圖和擬合值絕對誤差(率)兩個方面進行比較,結果均表明加權線性回歸效果好。該方法應用于教學,為教學內容的設計提供了新的思路,便于學生掌握并深入學習。
關鍵詞:異方差;加權最小二乘估計;殘差分析;權
文獻標識碼:A
回歸分析的發展經歷了很長的一段歷史,早在18世紀,F.Galton提出利用最小二乘原理進行回歸分析[1],從那時開始,回歸分析就越來越備受關注,但是隨著回歸分析的普及,在實際應用中往往出現違背線性回歸假設的情況,比如,隨機誤差異方差、隨機誤差存在序列相關性、數據觀測值異常等問題[2]。特別是對隨機誤差異方差的情況,加權線性回歸是對普通線性回歸的一種改進,但是文獻[3-4]中并未證明加權線性回歸的合理性。回歸診斷是回歸分析中必不可少的內容,由于回歸假設都是針對隨機誤差項提出的,所以要從分析隨機誤差項ε的估計量(殘差)入手,通過從殘差和殘差圖分析來考察模型的合理性[5]。
本文主要討論在隨機誤差異方差的情況下,怎樣建立合理、合適的模型。根據以往的經驗,處理隨機誤差異方差問題的方法有加權最小二乘法(WLS)、BOX-COX變換法和方差穩定性變換法,這些方法應用于實際,可以消除或者減弱異方差對擬合模型造成的不良影響。教科書上僅對加權線性回歸的原理有所介紹,但是并沒有涉及其本質內容。本文通過權、權函數、權倒數的性質揭示了加權線性回歸的本質,論證了其合理性。以北京市經濟開發區的銷售收入數據為例,利用加權最小二乘法建立數學模型,并且進行比較分析,模擬結果表明加權線性回歸比普通線性回歸有一定的改進之處。
1 線性回歸的基本假定[6-7]
線性回歸模型I(矩陣形式)
4 實例分析
4.1 問題描述
本文數據來源于文獻[6],因變量Y為各開發區的銷售收入(百萬元),自變量X1為截至1998年底各開發區累計招商數目,X2為招商企業注冊資本(百萬元),15個開發區的具體數據如表1所示。
從因變量Y的直方圖(圖1)也可以看出銷售收入信息呈右偏態分布,即數據具有異方差特征。
4.2 多元線性回歸模型
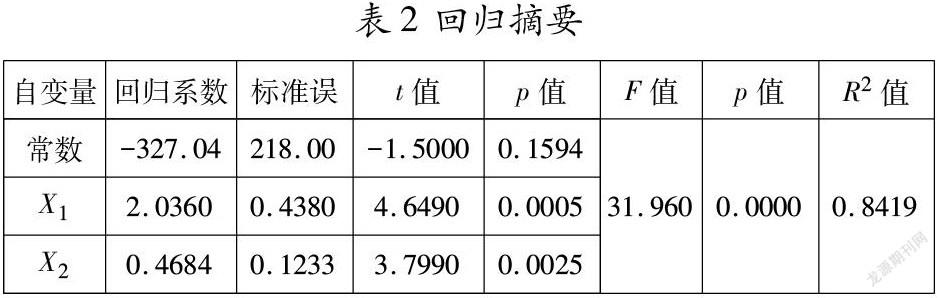
若對上述數據進行最小二乘回歸,得到結果如表2所示,造成回歸系數方差較大且不能通過顯著性檢驗的原因可能是異方差性;另外,模型的決定系數為0.8419,擬合度值并不高,有提高的可能性。
4.3 加權線性回歸模型的建立
由于4.2中普通殘差的絕對值與自變量X中X1的等級相關系數為0.4429,與X2的等級相關系數為0.7214,于是根據2.1,選擇X2構造權函數,即W=diag(1Xm1,1Xm2)。
根據對數似然值越大,回歸模型擬合效果越好的原則,表3列出了m值的選擇過程。
表3表明,當m=2.5時,對數似然統計量的值最大,于是m的最優值為2.5。同時,回歸模型結果如表4所示。
與表2相比,表4中常系數方差變小,且通過了顯著性檢驗,另外,模型決定系數為0.8494也大于之前的0.8419。
4.4 方法比較
對加權線性回歸模型做殘差圖,結果如下所示:
圖2中,從左至右圖形中的大部分散點并沒有向外側擴散,反而有收斂趨勢,可見“權”對異方差問題有一定的修正效果。
普通最小二乘和加權最小二乘的擬合值與殘差的比較結果如表5所示,顯然,加權最小二乘的效果較好。
4.5 回歸診斷
從圖示結果可以看出,圖3中殘差值并未出現極端上升或下降趨勢,是隨機均勻分布的。
結語
本文對多元加權線性回歸模型的原理與本質內容作了梳理,利用權倒數的性質,論證了加權線性回歸的參數估計也具有“最優”無偏性,同時結合數據案例驗證了加權線性回歸是解決異方差問題的有效途徑,不管是從殘差圖還是擬合值絕對誤差來講,效果都有所改善,回歸診斷結果也表現良好,即模型較優。文章的理論為以后的教學和學生學習運用加權線性回歸解決此類問題提供了充分的理論依據,為學生深入學習多元線性回歸模型提供了更多的可能性。
參考文獻:
[1]G.A.F.塞伯.線性回歸分析[M].方開泰,等,譯.北京:科學出版社,1987,1.
[2]Fabsitz,R.et al.Regression Analysis of Data with Correlated Errors.An Example from the NHLBI Twin Study[J].Chron.Dis.1985,38(2):165.
[3]何曉群,劉文卿.淺談加權最小二乘法及其殘差圖[J].統計研究,2006(4):53-57.
[4]林天水,陳佩樹.一元線性回歸中異方差的處理[J].統計與決策,2015(17):86-88.
[5]胡菊華.基于殘差分析的線性回歸模型的診斷與修正[J].統計與決策,2019(24):5-8.
[6]何曉群,劉文卿.應用回歸分析[M].北京:中國人民大學出版社,2012.
[7]茆詩松,程依明,濮曉龍.概率論與數理統計[M].北京:高等教育出版社,2012.
基金項目:2021年度陜西省教育科學“十四五”規劃一般課題“理實一體化的BOPPPS與‘六個下功夫相融合下數學教學模式創新研究”(編號:SGH21Y0293);2020年11月陜西省教育部產學合作協同育人項目“大數據下的數學課程教學模式改革與實踐”(編號:202002021019)
作者簡介:尚云艷(1986— ),女,陜西咸陽人,碩士,講師,研究方向:質量控制。FEA13F87-8594-4C1A-B251-F71883B69B98

