我國新凱恩斯菲利普斯曲線的經驗研究

戴曉兵 李志超

摘 要：本文基于1991—2020年的季度數據，通過構建適應性學習預期的狀態空間模型，采用卡爾曼濾波算法對我國學習型預期進行了測度，并將適應性學習預期、高階滯后適應性預期、理性預期和混合預期分別代入新凱恩斯菲利普斯曲線進行經驗研究，進而分析我國新凱恩斯菲利普斯曲線的混合學習預期特征。研究結果表明：首先，我國適應性學習預期并非完全理性預期，而是一種近理性預期，具有近理性特征。其次，我國新凱恩斯菲利普斯曲線具有高階滯后適應性預期與適應性學習預期的混合學習預期特征，同時高階滯后預期對通脹率的影響表現為逆向的通脹慣性。最后，適應性學習預期特征要強于高階滯后適應性預期特征，即相比于高階滯后適應性預期，適應性學習預期可以更好地反映我國通脹預期形成機制，但適應性學習預期相對于高階滯后適應性預期的強度受通脹率衡量指標的影響。

關鍵詞：新凱恩斯菲利普斯曲線;混合學習預期;適應性預期;適應性學習預期;高階滯后適應性預期;卡爾曼濾波

中圖分類號：F822.5? 文獻標識碼：A

文章編號：1000-176X（2022）04-0055-10

2019年下半年，我國整體宏觀經濟已表現出由弱企穩的增長趨勢，實際CPI通脹率也低于通脹目標水平，盡管政府公布的2020通脹率目標水平略高一點為3.5%，但實際CPI通脹率仍低于3%。一方面，是由于穩健的宏觀經濟調控政策;另一方面，也反映了國內公眾通脹預期較為穩定。央行從2010年開始加強通脹調控，2011年首次將穩定通脹預期和控制通脹率作為貨幣政策的首要目標，尤其是在通脹壓力較大時期更加注重通脹預期管理。（例如，2011年第一季度、2019年第四季度）。作為貨幣政策傳導機制之一的新凱恩斯菲利普斯曲線能夠較好地刻畫通脹與產出缺口和通脹預期的關系，因而成為各國央行制定貨幣政策的重要參考，這意味著如果能夠準確刻畫通脹率與產出缺口的權衡關系，央行可以通過調控產出缺口來實現通脹目標。但通脹預期會影響通脹率與產出缺口的權衡關系，因而合理評估通脹預期成為估計新凱恩斯菲利普斯曲線的關鍵。我國通脹預期具有怎樣的特征，是否具有近理性的學習型特征以及如何評估我國的學習型預期？受通脹預期影響，我國新凱恩斯菲利普斯曲線具有純粹預期特征還是混合預期特征，如果具有混合預期特征，那么是哪些預期的混合呢？本文正是基于上述問題，對我國通脹預期的學習型特征以及附帶混合學習預期的新凱恩斯菲利普斯曲線展開經驗研究。

一、文獻綜述

理性預期學派代表Lucas[1]指出，適應性預期會產生系統誤差，建議用理性預期替代適應性預期，且從理性預期的角度得到的菲利普斯曲線不論在短期還是在長期都是垂直的。Taylor [2]則對菲利普斯曲線做了改進，認為在粘性價格下，即使企業可以根據獲得的一切信息實現理性預期，菲利普斯曲線在短期也是傾斜的。那么菲利普斯曲線中的理性預期假設是否是合理的呢？Evans[3]認為，理性預期學派對預期的假設過于嚴格，放松理性預期假設將其轉變為適應性學習預期假設會更加符合公眾預期的形成機制。Cogley和Sargent[4]同樣建議使用適應性學習預期的形成方式來代替理性預期。在Evans和Honkapohja[5]提出預期形成的適應性學習理論的基礎上，相關文獻開始關注學習型預期的微觀基礎。Orphanides和Williams [6]通過對預期形成和參數調整機制的刻畫，使得公眾的通脹預期得以內生化，而且通過控制學習過程的相關參數，適應性學習預期可以較好地刻畫預期的有限理性內涵。Milani[7-8]發現，學習行為是通脹持久性的主要來源，前瞻性因素在通脹動態中起更重要的作用。Zhang和Kim[9]基于通脹預期調查數據和近似理性預期進行了研究證實，前瞻性行為在通脹驅動中作用較小。Sousa和Yetman[10]發現，新興經濟體的央行制定政策也越來越依靠預期變量，通過分析通脹預期的影響因素比較了不同通脹預期測算方法的差異，并發現新興經濟體通脹預期穩定態勢呈現逐漸加強的趨勢。Coibion等[11]通過隨機對照實驗研究了不同形式的溝通如何影響個體的通脹預期發現，影響公眾通脹預期形成的相關信息更多來自權威新聞且經濟主體獲取信息具有很強的自主性。

國內關于通脹預期的研究主要集中在我國通脹預期的測度和新凱恩斯菲利普斯曲線的特征方面。對通脹預期的測度方法大體分為三類：一是統計調查法。通過對公眾進行問卷調查，獲取公眾對未來通脹的判斷數據。如黎文靖和鄭曼妮[12]將央行定期發布的儲蓄問卷調查報告數據用滾動方法進行OLS回歸，算出預期通脹率。何啟志和姚夢雨[13]將學習型預期與調查問卷法結合起來，提出了遞歸法和滾動法兩種通脹預期測度方法。二是金融市場價格法。選取金融市場中相關指標對未來通脹率進行預測。如姚余棟和潭海鳴[14]利用卡爾曼濾波法，建立無套利仿射模型，從利率期限結構中分解出中長期通脹預期。三是模型估算法。利用宏觀經濟模型或計量模型等估計通脹預期。如卞志村和高潔超[15]基于常系數最小二乘法的固定收益學習模型對適應性學習預期進行了估算。國內學者也對我國新凱恩斯菲利普斯曲線的預期特征進行了廣泛研究，近期研究認為，很多學者認為，我國菲利普斯曲線具有慣性特征、混合預期特征或學習型預期特征。如李昊和王少平[16]發現，我國通脹形成機制具有理性預期與適應性預期相混合的特征。卞志村和胡恒強[17]則基于粘性信息給出了我國菲利普斯曲線具有混合預期特征的一個微觀解釋。何啟志和范從來[18]則發現，我國新凱恩斯菲利普斯曲線具有學習型預期特征。

適應性學習預期假設公眾能夠基于歷史信息不斷調整和更新預期行為，從而使得通脹預期逐漸趨于理性預期。相對于純粹理性預期，具有適應性學習預期的公眾在得到更新信息時會立即調整自身行為，使得通脹預期趨于理性而并非完全理性，更符合公眾預期的形成方式，且體現了公眾對于當期與預期信息的有限可得性。相對于純粹適應性預期，具有適應性學習預期的公眾考慮到了所有滯后通脹率包含的歷史信息，而非僅依賴一階滯后通脹率，體現了公眾對歷史信息的完全可得性。因此，適應性學習預期可以更好地刻畫公眾通脹預期的形成過程。從現有研究結論可以看出，我國新凱恩斯菲利普斯曲線具有混合預期特征和學習型預期特征，但并未將混合預期與學習型預期聯系起來，本文的研究結果表明，我國新凱恩斯菲利普斯曲線具有混合學習預期的特征。

本文的創新之處主要體現在兩個方面：一是基于卡爾曼濾波算法的適應性學習理論引入通脹預期測度中，并對我國通脹預期的認知偏差、無偏性和有效性進行檢驗。二是分別將理性預期和適應性預期與學習型預期組成混合預期，經驗分析了我國新凱恩斯菲利普斯曲線的混合學習預期特征。

本文結構安排如下：第二部分為研究設計，包括卡爾曼濾波適應性學習方程、單一預期與混合學習預期菲利普斯曲線模型的設定;第三部分為我國適應性學習預期的估計及檢驗，包括基于卡爾曼濾波適應性學習方程測度通脹預期，并進行認知偏差、無偏性和有效性檢驗;第四部分為我國混合學習新凱斯菲利普斯曲線的估計，包括基于適應性學習預期、適應性預期和理性預期，以及由適應性學習預期和其他兩種預期組合成混合學習預期對我國菲利普斯曲線的具體形式進行經驗分析;第五部分為主要結論與政策建議。

二、研究設計

（一）卡爾曼濾波適應性學習方程的設定

假定公眾對通脹預期π*t與實際通脹率πt的關系為：

πt=π*t+ε1t（1）

其中，ε1t為預期誤差。在適應性學習規則下，公眾在形成通脹預期時會參考歷史通脹預期π*t-i及通脹率的均值，即：

ln（π*t）=ρ1ln（π*t-1）+ρ2ln（π*t-2）+ρ3ln（π*t-3）+（1-ρ1-ρ2-ρ3）ln（）+ε2t（2）

將模型（2）在π*t=1處做一階泰勒展開有：

π*t=1+ρ1（π*t-1-1）+ρ2（π*t-2-1）+ρ3（π*t-3-1）+（1-ρ1-ρ2-ρ3）ln（）+ε2t（3）

將模型（1）和模型（3）分別作為觀測方程和狀態方程，則通脹預期的適應性學習方程可以寫成下面的狀態空間模型：

ξt=ct+Tξt-1+vt

Pt=Hξt+ut（4）

其中，H=100000000，ct=（1-ρ1-ρ2-ρ3）ln（）ln（）ln（），T=ρ1ρ2ρ3100010，ut=（ε1t，0，0），Pt=（πt，0，0），ξt=（π*t，π*t-1，π*t-2）T，vt=（ε2t，0，0）。本文通過卡爾曼濾波算法估計狀態空間模型（4），進而得到適應性學習預期π*t。

（二）新凱恩斯菲利普斯曲線的設定

新凱恩斯菲利普斯曲線的基準形式為：

πt=βπet+λyt+εt（5）

其中，λ為通脹與產出缺口的權衡系數，β為預期增廣系數，εt為隨機誤差項。設定πet存在三種預期形式：

首先，高階滯后適應性預期。將各階滯后通脹率乘以一定的權重并加總求和，即πet=Et-1πt=∑kj=1β0，jπt-j。

其次，適應性學習預期。將基于卡爾曼濾波算法得到的通脹預期作為適應性學習預期，即πet=π*t。

最后，理性預期。通常采用下一期實際通脹率作為當期通脹率的理性預期，即πet=Etπt+1=πt+1。為更全面地分析我國新凱恩斯菲利普斯曲線的形式，本文分別將三種預期以及將適應性學習預期與理性預期、適應性學習預期與高階滯后預期的混合預期代入模型（5）進行經驗分析。因此，本文經驗分析的新凱恩斯菲利普斯曲線共五種形式，分別為：

πt=∑kj=1β0jπt-j+λyt+εt（6）

πt=β1π*t+λyt+εt（7）

πt=β2Etπt+1+λyt+εt（8）

πt=β1π*t+β2Etπt+1+λyt+εt（9）

πt=∑kj=1β0jπt-j+β1π*t+λyt+εt（10）

（三）變量選取與數據處理

本文選取我國季度經濟數據進行參數估計，這是因為年度數據較少，不能反映每年數據變化的具體情況，影響模型估計的有效性，而月度數據的波動性較大，影響模型估計的穩定性。所有數據均來自中經網統計數據庫。

在通脹率衡量指標的選擇上，常用的指標有消費者價格指數CPI、生產者價格指數PPI和GDP平減指數等。PPI是反映生產企業提供的商品價格在一定時期內變化程度的指標，但其未將勞務產品的變化包含在內，因而不能全面反映出物價的變化。GDP平減指數的編制是以年為單位的，不能反映作為季度通脹率的變化程度，且數據樣本容量較小，不能得出參數的有效估計量。因此，本文選擇CPI作為通脹率的衡量指標，同時采用商品零售價格指數RPI進行穩健性檢驗。數據選取1991年1季度至2020年4季度的實際季度通脹率。由于CPI和RPI均為月度數據，需要將其加權平均轉化為季度數據，同時為縮短價格變化周期，本文沒有采用同比數據，而是采用季度環比數據進行研究。由于官方公布的CPI在1991—2000年、RPI在1991—2002年為同比數據，因而需要將同比數據轉化為環比數據。

本文還選取了固定資產投資額、社會消費品零售總額、進出口差額、流通中的現金M0、貨幣與準貨幣M2、實際通脹率、全國銀行間同業拆借市場7天加權平均利率和人民幣對美元的平均匯率等經濟系統中的其他變量，對我國適應性學習預期的有效性進行檢驗。鑒于部分數據的時間可得性，選擇2003—2020年的經濟數據進行檢驗。

在產出缺口的估計上，常用方法有生產函數法和趨勢分解法兩種，包括線性趨勢法、HP濾波法以及單變量和多變量的卡爾曼濾波法等。本文采用HP濾波法對產出缺口進行估計。其一，為避免通脹影響，將名義GDP轉換為實際GDP，以CPI為基礎的實際GDP1=名義GDP/（1+CPI），以RPI為基礎的實際GDP2=名義GDP/（1+RPI）。其二，為避免季節效應的影響，采用X12方法對實際GDP1和實際GDP2進行季節調整。其三，利用HP濾波法得到以CPI為基礎的產出缺口GDP_GAP1和以RPI為基礎的產出缺口GDP_GAP2。

三、我國適應性學習預期的估計及檢驗

（一）我國適應性學習預期的卡爾曼濾波估計

表1給出我國適應性學習預期的卡爾曼濾波估計結果。，圖1給出了實際通脹率與估計的預期通脹率的時序圖（左邊為CPI通脹率，右邊為RPI通脹率）。由表1可知，當用CPI衡量通脹預期時，滯后一期的預期、滯后二期的預期和滯后三期的預期對當期預期的影響程度分別為0.7305、，滯后二期的預期對當期預期的影響程度為0.9414和-0.7533，通脹均值對當期預期的影響程度為0.0814。當用RPI通脹預期時，滯后一期的預期、滯后二期的預期和滯后三期的預期對當期預期的影響程度分別為0.7260、0.9554和-0.7632，通脹均值對當期預期的影響程度為0.0818。可見，滯后通脹預期對當期預期的影響存在顯著差別，滯后一、二期通脹預期對當期預期存在正向影響，滯后三期通脹預期對當期預期存在負向影響，且通脹均值對當期預期的影響較小。

（二）我國適應性學習預期的檢驗

1.認知偏差檢驗

將適應性學習預期與實際通脹率的差值作為公眾對通脹率的認知偏差，即：

et=πt-π*t（11）

其中，et為認知偏差。若et>0，則說明公眾高估實際通脹率，若et<0，則說明公眾低估實際通脹率，若et=0，則表示公眾對實際通脹率既不存在高估也不存在低估，符合理性預期的假設。圖1分別給出了CPI通脹預期（左）和RPI通脹預期（右）認知偏差et的時序圖。零假設為：et的均值為0，結果表明，CPI通脹預期和RPI通脹預期的認知偏差均值為0的P值分別為0.1001和0.0712，在5%的顯著性水平下不能拒絕原假設，因而可以認為公眾對實際通脹率的認知偏差的均值為0 ，公眾對實際通脹率的預期既沒有高估也沒有低估。

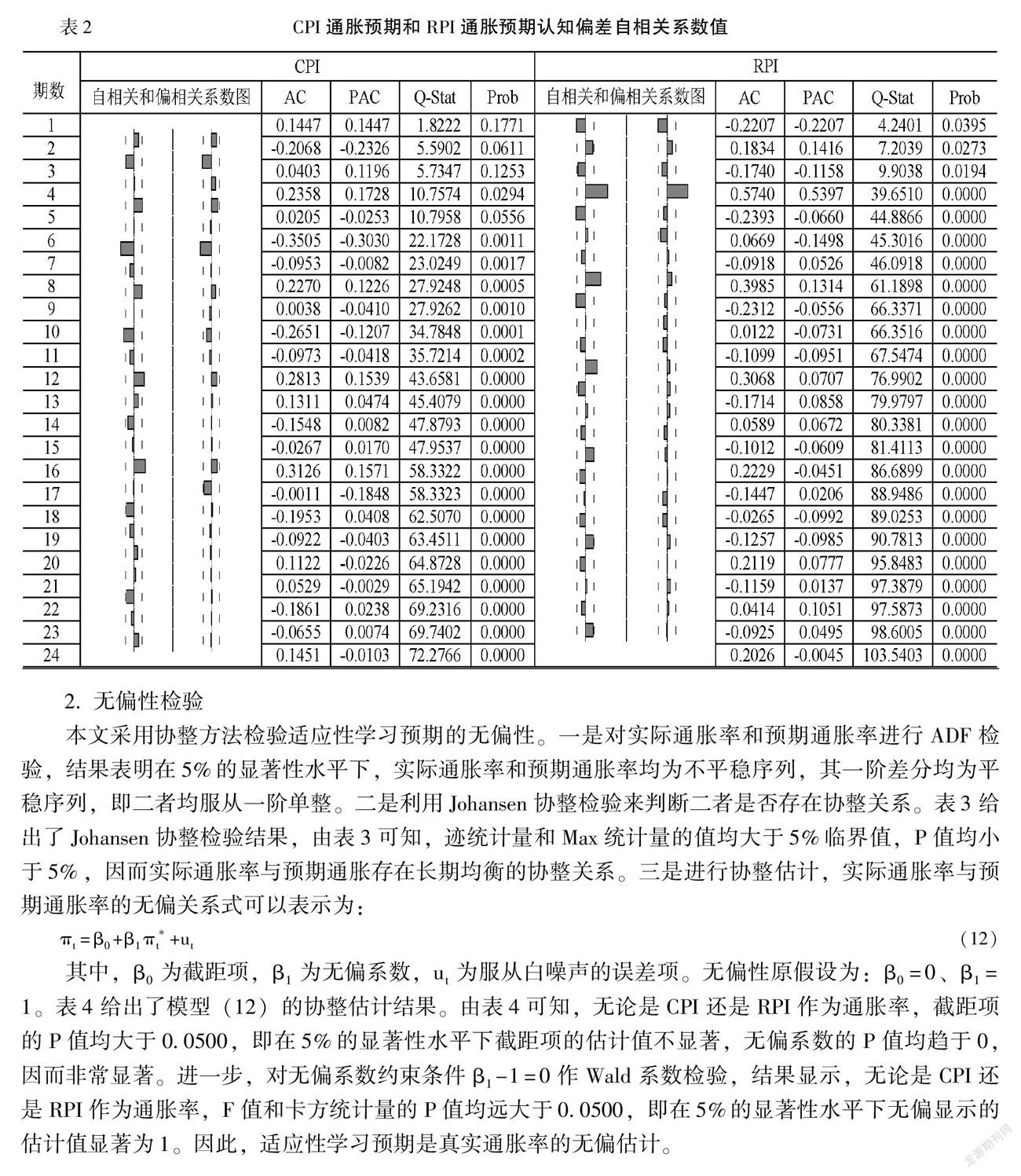
表2給出了CPI通脹預期和RPI通脹預期認知偏差自相關系數、偏自相關系數及其檢驗值。由表2可知，認知偏差前幾階的自相關系性比較明顯，但是隨著階數的滯后，認知偏差自相關性較為顯著的情況就會消失，根據Cuckierman和Meltzer[19]，如果公眾對通脹預期的誤差只在有限階數內存在相關性，則不能否認公眾預期為理性預期，因為具有完全理性的公眾對通脹預期也會出現這種情況，因而可以認為適應性學習預期的認知偏差符合理性預期的要求。同時，CPI通脹率只有2、6階偏自相關系數落在兩倍標準差之外，RPI通脹率只有4階偏自相關系數落在兩倍標準差之外，其余階數的偏自相關系數均不顯著，即當期公眾基于t期信息所得到的通脹預期認知偏差，在保證k期信息不變的條件下，與t+k期的認知偏差無相關性，即公眾在得到歷史信息以后，對將來任意兩期的認知偏差均可以近似看成與歷史信息不相關，可以進一步認為適應性學習預期認知偏差符合理性預期要求。

2.無偏性檢驗

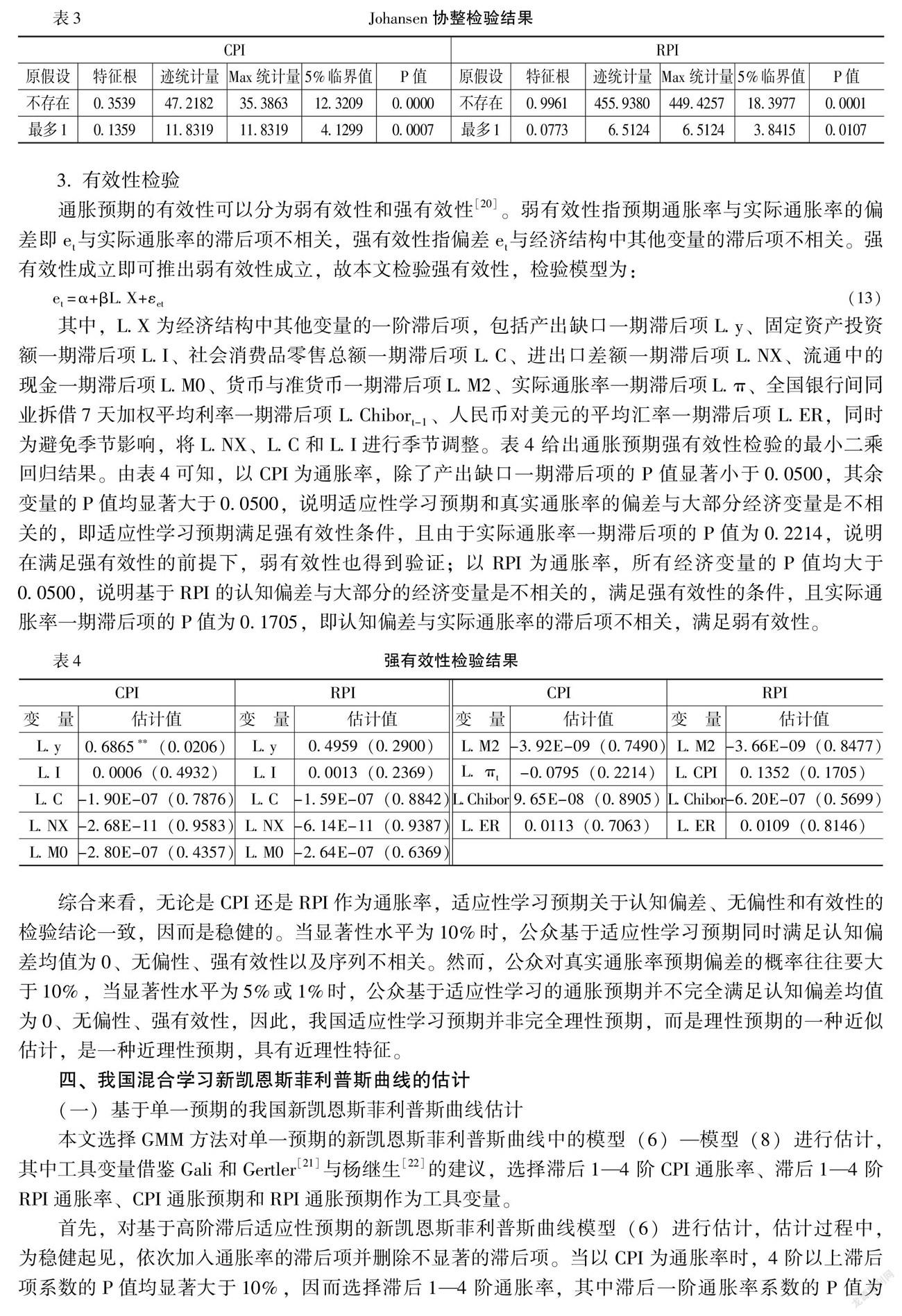
本文采用協整方法檢驗適應性學習預期的無偏性。一是對實際通脹率和預期通脹率進行ADF檢驗，結果表明在5%的顯著性水平下，實際通脹率和預期通脹率均為不平穩序列，其一階差分均為平穩序列，即二者均服從一階單整。二是利用Johansen協整檢驗來判斷二者是否存在協整關系。表3給出了Johansen協整檢驗結果，由表3可知，跡統計量和Max統計量的值均大于5%臨界值，P值均小于5%，因而實際通脹率與預期通脹存在長期均衡的協整關系。三是進行協整估計，實際通脹率與預期通脹率的無偏關系式可以表示為：

πt=β0+β1π*t+ut（12）

其中，β0為截距項，β1為無偏系數，ut為服從白噪聲的誤差項。無偏性原假設為：β0=0、β1=1。表4給出了模型（12）的協整估計結果。由表4可知，無論是CPI還是RPI作為通脹率，截距項的P值均大于0.0500，即在5%的顯著性水平下截距項的估計值不顯著，無偏系數的P值均趨于0，因而非常顯著。進一步，對無偏系數約束條件β1-1=0作Wald系數檢驗，結果顯示，無論是CPI還是RPI作為通脹率，F值和卡方統計量的P值均遠大于0.0500，即在5%的顯著性水平下無偏顯示的估計值顯著為1。因此，適應性學習預期是真實通脹率的無偏估計。

3.有效性檢驗

通脹預期的有效性可以分為弱有效性和強有效性[20]。弱有效性指預期通脹率與實際通脹率的偏差即et與實際通脹率的滯后項不相關，強有效性指偏差et與經濟結構中其他變量的滯后項不相關。強有效性成立即可推出弱有效性成立，故本文檢驗強有效性，檢驗模型為：

et=α+βL.X+εet（13）

其中，L.X為經濟結構中其他變量的一階滯后項，包括產出缺口一期滯后項L.y、固定資產投資額一期滯后項L.I、社會消費品零售總額一期滯后項L.C、進出口差額一期滯后項L.NX、流通中的現金一期滯后項L.M0、貨幣與準貨幣一期滯后項L.M2、實際通脹率一期滯后項L.π、全國銀行間同業拆借7天加權平均利率一期滯后項L.Chibort-1、人民幣對美元的平均匯率一期滯后項L.ER，同時為避免季節影響，將L.NX、L.C和L.I進行季節調整。表4給出通脹預期強有效性檢驗的最小二乘回歸結果。由表4可知，以CPI為通脹率，除了產出缺口一期滯后項的P

值顯著小于0.0500，其余變量的P值均顯著大于0.0500，說明適應性學習預期和真實通脹率的偏差與大部分經濟變量是不相關的，即適應性學習預期滿足強有效性條件，且由于實際通脹率一期滯后項的P值為0.2214，說明在滿足強有效性的前提下，弱有效性也得到驗證;以RPI為通脹率，所有經濟變量的P值均大于0.0500，說明基于RPI的認知偏差與大部分的經濟變量是不相關的，滿足強有效性的條件，且實際通脹率一期滯后項的P值為0.1705，即認知偏差與實際通脹率的滯后項不相關，滿足弱有效性。

綜合來看，無論是CPI還是RPI作為通脹率，適應性學習預期關于認知偏差、無偏性和有效性的檢驗結論一致，因而是穩健的。當顯著性水平為10%時，公眾基于適應性學習預期同時滿足認知偏差均值為0、無偏性、強有效性以及序列不相關。然而，公眾對真實通脹率預期偏差的概率往往要大于10%，當顯著性水平為5%或1%時，公眾基于適應性學習的通脹預期并不完全滿足認知偏差均值為0、無偏性、強有效性，因此，我國適應性學習預期并非完全理性預期，而是理性預期的一種近似估計，是一種近理性預期，具有近理性特征。

四、我國混合學習新凱恩斯菲利普斯曲線的估計

（一）基于單一預期的我國新凱恩斯菲利普斯曲線估計

本文選擇GMM方法對單一預期的新凱恩斯菲利普斯曲線中的模型（6）—模型（8）進行估計，其中工具變量借鑒Gali和Gertler[21]與楊繼生[22]的建議，選擇滯后1—4階CPI通脹率、滯后1—4階RPI通脹率、CPI通脹預期和RPI通脹預期作為工具變量。

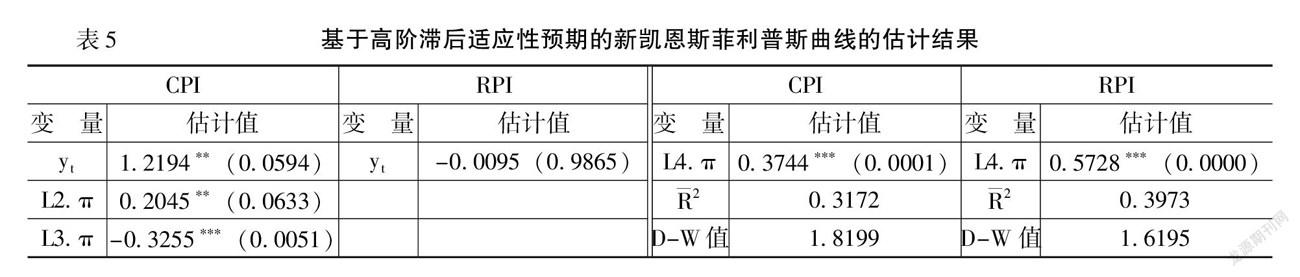
首先，對基于高階滯后適應性預期的新凱恩斯菲利普斯曲線模型（6）進行估計，估計過程中，為穩健起見，依次加入通脹率的滯后項并刪除不顯著的滯后項。當以CPI為通脹率時，4階以上滯后項系數的P值均顯著大于10%，因而選擇滯后1—4階通脹率，其中滯后一階通脹率系數的P值為0.4905，參數估計值不顯著，因而刪除重新估計，表5給出了估計結果。由表5可知，滯后2—3階通脹率的系數、產出缺口與通脹率的權衡系數至少在10%水平下均顯著。

當以RPI為通脹率時，4階以上滯后項系數的P值均顯著大于10%，因而選擇滯后1—4階通脹率，其中滯后1—3階通脹率的系數估計值不顯著，因而選擇滯后4階通脹率進行估計。結果顯示，產出缺口與通脹率的權衡系數不顯著，這與CPI為通脹率的結論不一致，但4階滯后項系數顯著至少說明我國新凱恩斯菲利普斯曲線具有高階滯后適應性預期的特征。

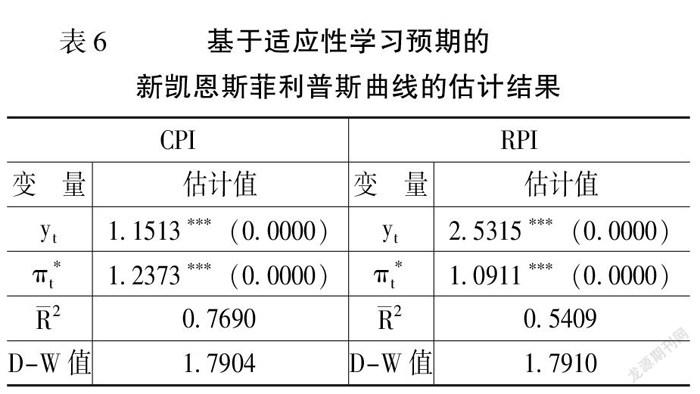
其次，對基于適應性學習預期的新凱恩斯菲利普斯曲線模型（7）進行估計，如表6所示。由表6可知，當以CPI為通脹率時，產出缺口與通脹率的權衡系數顯著大于0，且模型擬合優度顯著大于模型（6），因而模型（7）較優，同時適應性學習預期的系數為正值且P值趨于0，說明適應性學習預期對當期通脹率存在顯著的正向影響。當以RPI為通脹率時，產出缺口與通脹率的權衡系數和適應性學習預期系數均顯著，與前述結論一致。相對于高階滯后適應性預期，適應性學習預期可以更好地刻畫通脹預期對當期通脹率的影響，因而我國新凱恩斯菲利普斯曲線還具有適應性學習預期的特征。

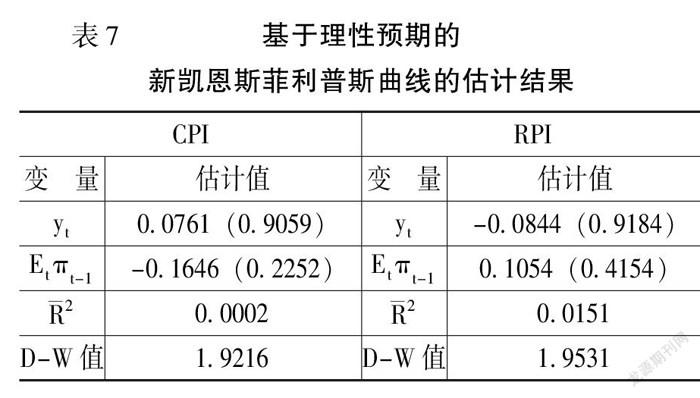
最后，對基于理性預期的新凱恩斯菲利普斯曲線模型（8）進行估計，如表7所示。由表7可知，無論是以CPI為通脹率還是以RPI為通脹率，產出缺口與通脹率的權衡系數、理性預期系數均不顯著，且模型擬合優度較小，因而單一理性預期不能很好地刻畫通脹預期對當期通脹率的影響，說明我國新凱恩斯菲利普斯曲線不具有純粹理性預期的特征。

（二）基于混合學習預期的我國新凱恩斯菲利普斯曲線估計

本文設定的混合學習預期有兩種：一種是理性預期與適應性學習預期的混合學習預期;一種是高階滯后適應性預期與適應性學習預期的混合學習預期。估計過程與單一預期一致。

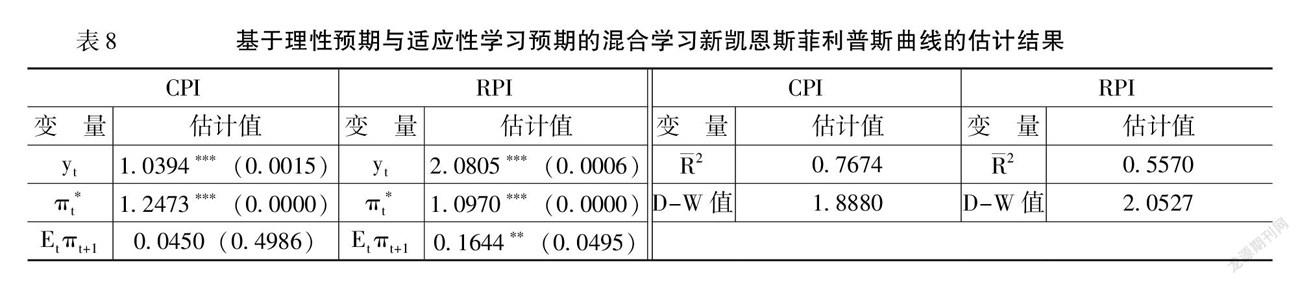
首先，對基于第一種混合學習預期的新凱恩斯菲利普斯曲線模型（9）進行估計，如表8所示。由表8可知，當以CPI為通脹率時，產出缺口與通脹率的權衡系數、適應性學習預期系數均在1%的水平下顯著，但理性預期系數卻并不顯著。對比模型（9）與模型（7）的產出缺口與通脹率的權衡系數及適應性學習預期系數，發現二者的系數差別不大，模型（7）中的權衡系數和學習預期系數分別為1.1513和1.2373，模型（9）的權衡系數和學習預期系數分別為1.0394和1.2473，且均在1%水平下顯著。這表明，理性預期的引入并不能有效改變新凱恩斯菲利普斯曲線模型（7）的預期特征，同時考慮到理性預期系數不顯著，因此，我國新凱恩斯菲利普斯曲線不具有理性預期與適應性學習預期的混合學習預期特征，但具有適應性學習預期特征。當以RPI為通

脹率時，產出缺口和通脹率的權衡系數、適應性學習預期系數在1%的水平下顯著，同時菲利普斯曲線模型（9）和模型（7）的產出缺口與通脹率的權衡系數及適應性學習預期系數估計值也差別不大且均在1%水平下顯著，新凱恩斯菲利普斯曲線模型（7）中的權衡系數和學習預期系數分別為2.5315和1.0911，新凱恩斯菲利普斯曲線模型（9）的權衡系數和學習預期系數分別為2.0805和1.0970。盡管新凱恩斯菲利普斯曲線模型（9）的理性預期系數在5%的水平下顯著，但其系數值（0.1644）相對于權衡系數和學習系數要小得多，理性預期對通脹率的影響依然不大，理性預期與適應性學習預期的混合學習預期特征仍不顯著，但具有較強的適應性預期特征，這與以CPI為通脹率的結論是一致的。

其次，對基于第二種混合學習預期的新凱恩斯菲利普斯曲線模型（10）進行估計，估計過程中，為穩健起見，依次加入通脹率的滯后項并刪除不顯著的滯后項。當以CPI為通脹率時，6階以上滯后項系數的P值均顯著大于10%，因而選擇滯后1—6階通脹率，其中滯后3階通脹率系數的P值為0.5669，參數估計值不顯著，因而刪除重新估計，表9給出了最終估計結果。由表9可知，產出缺口與通脹率的權衡系數和適應性學習預期系數均在1%的水平下顯著，且適應性學習預期對通脹率存在正向影響，這與新凱恩斯菲利普斯曲線模型（7）和模型（9）的結論一致。對比新凱恩斯菲利普斯曲線模型（10）和模型（7）的權衡系數和學習預期系數，可以發現權衡系數下降，由1.1513變為0.4829，而學習預期系數上升，由1.2373變為1.9605，這表明，適應性預期的引入增強了我國新凱恩斯菲利普斯曲線的學習預期特征。與基于高階滯后適應性預期的新凱恩斯菲利普斯曲線模型（6）對比，適應性學習預期的引入顯著提高了調整擬合優度，因而可以更好地刻畫我國新凱恩斯菲利普斯曲線的預期特征。對于通脹率的高階滯后項，1、2、4、5和6階滯后項系數估計值均顯著，而在五個滯后項的系數中，只有5階滯后項的系數是正值，其他階數滯后項的系數均為負值，其中2階滯后項系數的絕對值最大，因而在高階滯后預期中對通脹率的影響最大。進一步，五個滯后項的系數之和為-0.8876，系數之和的絕對值小于適應性學習系數，因而適應性學習預期特征要強于高階滯后預期特征。這與前面的結論也一致，即相比于高階滯后預期，適應性學習預期可以更好地反映我國的通脹預期形成機制。在基于混合預期的新凱恩斯菲利普斯曲線中，通脹率的滯后項反映了通脹慣性和貨幣政策的時滯性，但是在基于適應性學習預期的條件下，通脹率滯后項的系數之和卻小于0，這意味著我國新凱恩斯菲利普斯曲線具有適應性預期與適應性學習預期的混合學習預期特征，同時適應性預期對通脹率的影響表現為逆向的通脹慣性。

當以RPI為通脹率時，6階以上滯后項的系數P值均顯著大于10%，因而選擇滯后1—6階通脹率，其中滯后3—5階通脹率的系數估計值不顯著，因而刪除重新估計，表9給出了最終估計結果。由表9可知，產出缺口與通脹率的權衡系數、適應性學習預期系數均在1%的水平下顯著，且適應性學習預期對通脹率存在正向影響，這與CPI為通脹率的結論一致，也與新凱恩斯菲利普斯曲線模型（7）和模型（9）的結論一致。對比新凱恩斯菲利普斯曲線模型（10）與模型（7）的權衡系數與學習預期系數發現權衡系數下降，由2.0805變為1.3142，而學習預期系數上升，由1.0970變為1.3986，這同樣說明了適應性預期的引入增強了我國新凱恩斯菲利普斯曲線的學習預期特征。與新凱恩斯菲利普斯曲線模型（6）對比，適應性學習預期的引入同樣顯著提高了調整擬合優度。對于通脹率的高階滯后項，1、2、6階滯后項系數估計值均顯著，而在三個滯后項的系數中，只有1階滯后項的系數是正值，其他階數滯后項的系數均為負值，三個滯后項的系數之和為-0.3191，系數之和的絕對值小于適應性學習系數，因而我國新凱恩斯菲利普斯曲線具有適應性預期與適應性學習預期的混合學習預期特征，但適應性學習預期特征要強于高階滯后預期特征。通脹率滯后項的系數之和小于0，同樣說明適應性預期對通脹率的影響表現為逆向的通脹慣性。這與以CPI為通脹率的結論一致。

雖然基于第二種混合學習預期可以較好地刻畫出兩種不同通脹率指標下的我國新凱恩斯菲利普斯曲線的形式，但是估計結果還是有所差異。以CPI為通脹率的新凱恩斯菲利普斯曲線模型（10）包含五階滯后項，而以RPI為通脹率的菲利普斯曲線模型（10）則包含三階滯后項。將新凱恩斯菲利普斯曲線中通脹率滯后項系數和的絕對值與適應性學習預期項的系數相比，則以CPI為通脹率的比值為0.5016，以RPI為通脹率的比值為0.2268，說明以RPI為通脹率的新凱恩斯菲利普斯曲線的適應性學習預期的特征更強，高階滯后適應性預期對通脹率的影響相對較小。因而在不同通脹率指標下，通脹預期對新凱恩斯菲利普斯曲線影響程度不同，即采用不同的指標來

衡量通脹率，高階滯后適應性預期和適應性學習預期的影響程度會不同，因此，貨幣當局在制定貨幣政策時，應首先明確關心通脹率指標，然后才能有的放矢地穩定公眾通脹預期以及調整通脹慣性。而無論采用哪種通脹率指標，貨幣當局都應提高貨幣政策的信譽度、透明度和獨立性，并適度減少貨幣政策的調整頻率，這樣既能夠穩定公眾通脹預期，又能夠減少通脹慣性的逆向影響。

五、主要結論與政策建議

本文基于1991—2020年的季度數據，通過構建適應性學習預期的狀態空間模型，采用卡爾曼濾波算法對我國學習型通脹預期進行了測度，并將適應性學習預期、高階滯后適應性預期、理性預期及其混合預期分別代入新凱恩斯菲利普斯曲線進行經驗研究，進而分析我國新凱恩斯菲利普斯曲線的混合學習預期特征。同時為使結論穩健，本文分別以消費者價格指數CPI和商品零售價格指數RPI為通脹率指標進行檢驗。結果表明：

第一，當顯著性水平為10%時，公眾基于適應性學習預期同時滿足認知偏差均值為0、無偏性、強有效性以及序列不相關;當顯著性水平為5%或1%時，公眾基于適應性學習預期并不完全滿足認知偏差均值為0、無偏性、強有效性。因此，我國適應性學習預期并非完全理性預期，而是一種近理性預期，具有近理性特征。

第二，我國新凱恩斯菲利普斯曲線具有高階滯后適應性預期與適應性學習預期的混合學習預期特征，同時高階滯后適應性預期對通脹率的影響表現為逆向的通脹慣性。

第三，適應性學習預期特征要強于高階滯后適應性預期特征，即相比于高階滯后適應性預期，適應性學習預期可以更好地反映我國通脹預期形成機制，但適應性學習預期相對于高階滯后預期的強度受通脹率衡量指標的影響。

基于此，筆者提出如下政策建議：

第一，由于不同通脹率衡量指標所對應的新凱恩斯菲利普斯曲線的具體形式不同，具體表現為適應性學習預期對高階滯后預期的相對強度不同，或者說適應性學習預期和高階滯后預期對通脹率的影響程度不同，因而貨幣當局在制定政策時，應首先明確關心的是哪種通脹率指標可以更好地對我國新凱恩斯菲利普斯曲線進行刻畫，這樣才能保證貨幣政策有的放矢和有效性。

第二，從我國近年來貨幣政策的實踐來看，宏觀經濟運行本身具有復雜多變的特征，加之近兩年新冠肺炎疫情的沖擊，經濟發展受到嚴重挑戰，使得公眾難以形成穩定預期，而我國新凱恩斯菲利普斯曲線具有適應性學習預期和高階滯后適應性預期的混合學習預期特征，既包含了學習特征，又包含了慣性特征，因此，貨幣政策調控應從兩個方面完善：一方面，對于適應性學習預期，貨幣當局應注意對公眾預期的引導，防止公眾學習程度出現過高或過低;另一方面，對于高階滯后適應性預期，貨幣當局應適度控制貨幣政策的調整頻率。

第三，在適應性學習預期的引導上，貨幣當局應重視公眾適應性預期的形成機制。雖然本文估計的適應性學習預期可以很好地刻畫真實通脹率，但公眾的學習機制是一個不斷調整的過程，在這一調整過程中，央行溝通和貨幣政策工具實施至關重要。如果貨幣當局溝通邊界有限造成所提供的信息不如私人信息準確，或者對主要實施的貨幣政策工具并沒有給予足夠的重視，則貨幣當局溝通反而會造成公眾信息損失，其政策實施也會與公眾的預期存在偏差。為引導適應性學習預期趨于理性預期，貨幣當局應該提高貨幣政策的透明度與可信度，提高與公眾溝通的信息質量，確保公眾從貨幣當局的溝通中得到的信息要大于通過其他方式所得到的信息，避免公眾形成預期過程中的信息損失。同時貨幣當局應注重聲譽和信用，保持貨幣政策工具實施的一致性和連貫性。，避免由于主要貨幣政策工具實施的轉換導致貨幣政策出現動態不一致性。

參考文獻：

[1] Lucas，R.E.Expectations and the Neutrality of Money [J].Journal of Economic Theory，1972，4（2）：103-124.

[2] Taylor，J.B.Aggregate Dynamics and Staggered Contracts [J].Journal of Political Economy，1980，88（1）：1-23.

[3] Evans，G.Expectations Stability and the Multiple Equilibria Problem in Liner Rational Expectations Models [J].Quarterly Journal of Economics，1985，100（4）：1217-1233.

[4] Cogley，T.，Sargent，T.J.The Conquest of US Inflation： Learning and Robustness to Model Uncertainty[J].Review of Economic Dynamics，2005，8（2）：528-563.

[5] Evans，G.W.，Honkapohja，S.Learning and Expectations in Macroeconomics[M].Princeton ：Princeton University Press，2001.

[6] Orphanides，A.，Williams，J.Imperfect Knowledge，Inflation Expectations，and Monetary Policy[R].NBER Working Paper No.9884，2004.

[7] Milani，F.Adaptive Learning and Inflation Persistence[R].University of California-Irvine Working Paper No.50607，2005.

[8] Milani，F.Expectations，Learning and Macroeconomic Persistence[R].University of California-Irvine Working Paper No.50608，2005.

[9] Zhang，C.，Kim，O.D.H.The New Keynesian Phillips Curve： From Sticky Inflation to Sticky Prices[J].Journal of Money，Credit and Banking，2008，40（4）：667-699.

[10] Sousa，R.，Yetman，J.Inflation Expectations and Monetary Policy[R].BIS Papers，2016.

[11] Coibion，O.，Gordnichenko，Y.，Weber，M.Monetary Policy Communications and Their Effects on Household Inflation Expectations[R].NBER Working Paper No.25482，2019.

[12] 黎文靖，鄭曼妮.通貨膨脹預期、企業成長性與企業投資[J].統計研究，2016，（5）：34-42

[13] 何啟志，姚夢雨.中國通脹預期測度及時變系數的菲利普斯曲線[J].管理世界，2017，（5）：66-78.

[14] 姚余棟，譚海鳴.中國金融市場通脹預期——基于利率期限結構的量度[J].金融研究，2011，（6）：61-70.

[15] 卞志村，高潔超.適應性學習、宏觀經濟預期與中國最優貨幣政策[J].經濟研究，2014，（4）：32-46.

[16] 李昊，王少平.我國通貨膨脹預期和通貨膨脹粘性[J].統計研究，2011，（1）： 43-48.

[17] 卞志村，胡恒強.粘性價格、粘性信息與中國菲利普斯曲線[J].世界經濟，2016，（4）：22-43.

[18] 何啟志，范從來.學習型預期與中國擴展的新菲利普斯曲線的研究[J].金融研究，2014，（9）：34-52.

[19] Cuckierman，A.，Meltzer，A.H.A Theory of Ambiguity，Credibility and Inflation Under Discretion and Asymmetric Information[J].Econometrica，1986，54（5）：1028-1099.

[20] Mehra，Y.P.Survey Measures of Expected Inflation： Revisiting the Issues of Predictive Content and Rationality[J].Economic Quarterly，2002，88（3）： 17-36.

[21] Gali，J.，Gertler，M.Inflation Dynamics： A Structural Econometric Analysis[J].Journal of Monetary Economics，1999，44（2）： 195-222.

[22] 楊繼生.通脹預期、流動性過剩與中國通貨膨脹的動態性質[J].經濟研究，2009，（1）：106-117.

An empirical Study on the New Keynesian Phillips Curve in China Based on Mixed Learning Expectation

DaiXiaobing? Guo Kai，Li Zhichao

Abstract：Based on quarterly data from 1991 to 2020，this paper uses the Kalman filter algorithm to measure China's learning inflation expectations by constructing an adaptive learning inflation expectations state space model.And the adaptive learning expectations，high-order lagging adaptive expectations，rational expectations and their mixed expectations are respectively substituted into the New Keynes Phillips Curve for empirical analysis，so as to analyze the characteristics of mixed learning expectations of China's New Keynes Phillips Curve.Empirical research shows that： （1） China's adaptive learning inflation expectations are not completely rational expectations，but a near-rational expectation with near-rational characteristics; （2） China's New Keynesian Phillips curve has the characteristics of mixed learning expectation of high-order lag adaptive expectation and adaptive learning expectation.At the same time，the impact of high-order lag expectation on inflation rate is reverse inflation inertia;（3） The characteristics of adaptive learning expectation are stronger than high-order lag expectation，that is，compared with high-order lag expectation，adaptive learning expectation can better reflect the formation mechanism of inflation expectation in China.However，the strength of adaptive learning expectation relative to high-order lag expectation is affected by the measurement index of inflation rate.

Key words：Adaptive Learning Expectation;New Keynesian Phillips Curve;Hybrid Expectation; Kalman Filter

（責任編輯：劉 艷）

收稿日期：2021-12-03

基金項目：教育部人文社會科學規劃基金項目“金融穩定、前瞻性擴展貨幣政策規則與不確定性：基于LRE模型的實證分析與檢驗研究”（18YJA790027）;遼寧省教育廳高等學校基本科研項目“數字普惠金融與遼寧綠色全要素生產率”（LJKR0432）

作者簡介：戴曉兵（1986-），女，遼寧遼陽人，講師，博士，主要從事金融市場研究。E-mail： daixiaobing_800@sina.com

李志超（1995-），男，遼寧鐵嶺人，碩士研究生，主要從事貨幣政策研究。E-mail：252182806@qq.com]