基于流固雙向耦合的轎車氣動與流致振動特性

胡興軍，王澤偉，于果，劉飛，蘭巍，余天明，桑濤

（吉林大學汽車仿真與控制國家重點實驗室，吉林長春 130022）

汽車空氣動力學由于影響汽車的燃油經濟性，操縱穩(wěn)定性及安全性等已經成為汽車開發(fā)中不可缺少的一部分，傳統(tǒng)計算流體力學仿真只考慮流體對車輛的氣動特性影響，忽略了車輛振動與外流場的耦合作用，從而導致得到的數(shù)據(jù)與實際情況存在一定偏差.尤其在高速行駛工況下，流固耦合效應加劇將更加影響車輛行駛的穩(wěn)定性.因此，在計算流體力學中考慮流固耦合效應，采用流體與固體軟件協(xié)同仿真的方法［1］，使數(shù)值仿真結果更為精準，可以更好地開展車輛氣動特性和振動特性研究.對提高車輛的穩(wěn)定性、舒適性設計提供參考依據(jù).

許多研究人員進行了流固耦合相關研究，文獻［2］在時域內對剪切三角翼的流固耦合效應進行了研究.文獻［3］對汽車外后視鏡風致振機理與特性采用流固耦合手段進行了探究.文獻［4］建立了風-車（列車）-橋耦合系統(tǒng)模型，研究環(huán)境風對耦合系統(tǒng)的振動影響，計算結果表明流致振動現(xiàn)象嚴重影響車輛穩(wěn)定性.李田［5］利用任意拉格朗日歐拉法實現(xiàn)列車的流固耦合仿真，指出了風激振對高速列車運行安全性的影響.當前的流固耦合數(shù)值仿真研究對象一般為列車、機翼或建筑等，對汽車實車研究多采用單純空氣動力學、多體動力學方法或者單向流固耦合數(shù)值仿真研究.

針對以上所述關于車輛流固耦合氣動及流致振動研究的不足，本文以某實車模型為研究對象，將考慮雙向流固耦合效應的數(shù)值仿真與傳統(tǒng)計算流體力學仿真進行對比，探究兩者流場及氣動力差異的產生機理，并進行整車風激振特性研究.

1 流固耦合理論基礎

流固耦合數(shù)值仿真需要將流體域與固體域聯(lián)立協(xié)同求解，兩相交界面上的數(shù)據(jù)傳遞是關鍵問題所在.由于固體域與流體域計算采用的分別是拉格朗日和歐拉描述方式，在仿真過程中，當固體產生較大位移時，兩者交界面上的節(jié)點不再重合，因此仿真出錯.為解決此問題，采用任意拉格朗日歐拉（ALE）法［6］即引入?yún)⒖甲鴺讼担梢赃B續(xù)追蹤邊界，交界面的網(wǎng)格節(jié)點跟隨固體結構節(jié)點運動，防止網(wǎng)格畸變.此外，流固耦合交接面上需要滿足位移與力平衡的動力學條件［7-8］.

式中：df，ds為流體節(jié)點與固體節(jié)點位移.

式中：τ(f/s)為應力（流體/固體）；n為單位法向量分量.

節(jié)點坐標可以在流體中通過已知的運動學條件求得，在流固交界面上將積分計算出的合力施加到對應固體節(jié)點上［9］：

式中：hd為固體節(jié)點位移；ds為微元面積.

流固耦合體系里解向量為：

Xsf是耦合交界面節(jié)點上的解，分別位于固體與流體上.

已知ds=ds(Xs)，τf=τf(Xf)，耦合系統(tǒng)的有限元方程式如下所示：

式中，F(xiàn)f是流體方程；Fs是結構方程.

進行流固耦合瞬態(tài)仿真計算時，固體的變形會影響流場結構，因此在流體計算時需要用動網(wǎng)格技術來完成網(wǎng)格的更新.相關動網(wǎng)格參數(shù)設置完成后，變形區(qū)域的網(wǎng)格即會進行自適應變形.本文中動網(wǎng)格方法采用迭代法，主要分為彈簧光順，動態(tài)分層和局部網(wǎng)格重劃三個模型，彈簧光順模型核心思想為在計算中，假定網(wǎng)格節(jié)點之間為平衡狀態(tài)下的彈簧系統(tǒng)，節(jié)點位移之后根據(jù)Hooke 定律經過迭代確定新平衡狀態(tài)下的網(wǎng)格節(jié)點坐標.動態(tài)分層模型多用結構化網(wǎng)格中，在網(wǎng)格運動邊界根據(jù)其運動狀態(tài)增減網(wǎng)格層數(shù).局部網(wǎng)格重劃模型主要應用于非結構網(wǎng)格中，對運動區(qū)域的網(wǎng)格進插值計算進而重新劃分.本文采用的主要為局部網(wǎng)格重劃模型.

迭代法可以較好地處理結構大位移運動，適合車身姿態(tài)變化的情況，但不足的是由于需要進行大量插值計算，迭代動網(wǎng)格方法會延長計算時間，降低計算效率［10-14］.

2 基于流固耦合效應的車輛數(shù)值仿真

本章考慮流固耦合效應，對實車在流場中的氣動力及風激振現(xiàn)象展開研究.

2.1 模型及網(wǎng)格參數(shù)

采用某轎車實車模型，長度×寬度×高度為4.4 m×2.0 m×1.5 m，正投影面積：2.18 m2.對車輛的細節(jié)進行簡化及平整化處理，并將實車的懸架及輪胎等效為彈性單元，使用貼體性好的5～20 mm 尺寸漸變三角形網(wǎng)格對模型進行網(wǎng)格劃分，如圖1 所示.在輪胎和車體之間加入彈性阻尼單元以代替懸架和車輪等彈性結構，車身及其部件的形變忽略不計，并將車輪底部設置為固定端以便研究車身在流固耦合仿真中的位移情況，彈性阻尼單元根據(jù)實車條件等效剛度設為20 000 N/m，阻尼150N/（m·s-1），固體計算采用ABAQUS軟件中瞬態(tài)隱式方法求解.

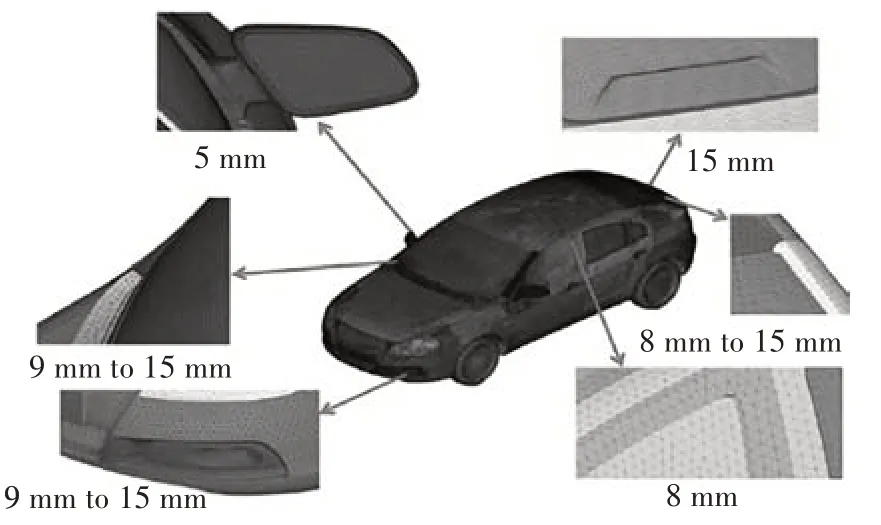
圖1 實車網(wǎng)格劃分Fig.1 Real vehicle meshing

流固耦合計算對計算資源有一定要求，在保證精度的前提下，也要考慮硬件條件.流體軟件使用STAR-CCM+，并對流體網(wǎng)格進行網(wǎng)格無關性驗證，網(wǎng)格數(shù)量與阻力系數(shù)的關系見圖2.隨著流體網(wǎng)格數(shù)量逐漸增加，可以發(fā)現(xiàn)，當網(wǎng)格數(shù)超過900 萬時，阻力系數(shù)逐漸穩(wěn)定在0.332左右，另外邊界層厚度為面網(wǎng)格尺寸的1/3，層數(shù)設定為5 層.最終確定流體域尺寸設為10 倍車長，9 倍車寬，5 倍車高［15-17］，并設置兩個加密區(qū)，最終使用20～300 mm 的流體網(wǎng)格［18-22］.如圖3所示，網(wǎng)格數(shù)量大約為910萬.

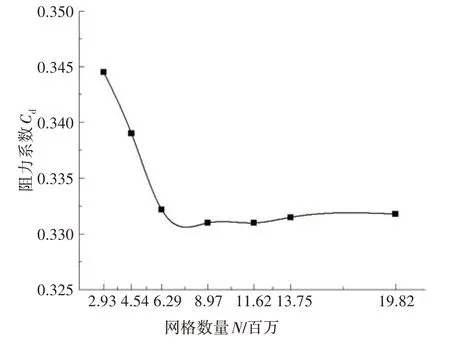
圖2 阻力系數(shù)與流體網(wǎng)格數(shù)Fig.2 Drag coefficient and fluid mesh number

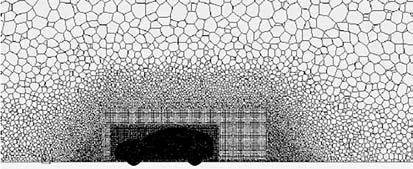
圖3 車輛外流場網(wǎng)格方案Fig.3 Grid scheme of vehicle flow field

本文采用瞬態(tài)流固耦合數(shù)值仿真，使用k -ωSST湍流模型［23］，時間步長設為0.001 s，流體與固體的數(shù)據(jù)傳遞通過車身作為耦合交界面實現(xiàn)［24］.

2.2 氣動性能分析

本節(jié)對整車氣動阻力和氣動升力展開研究，如圖4 所示分別為是否考慮流固耦合效應數(shù)值仿真中阻力與升力對比圖.圖5 為升阻力差異率曲線，圖6為兩種仿真方法波動情況.圖7為速度為120km/h時（常用高速工況）兩種仿真方法的氣動升力對比.（FSI為流固耦合，NO-FSI為非流固耦合）

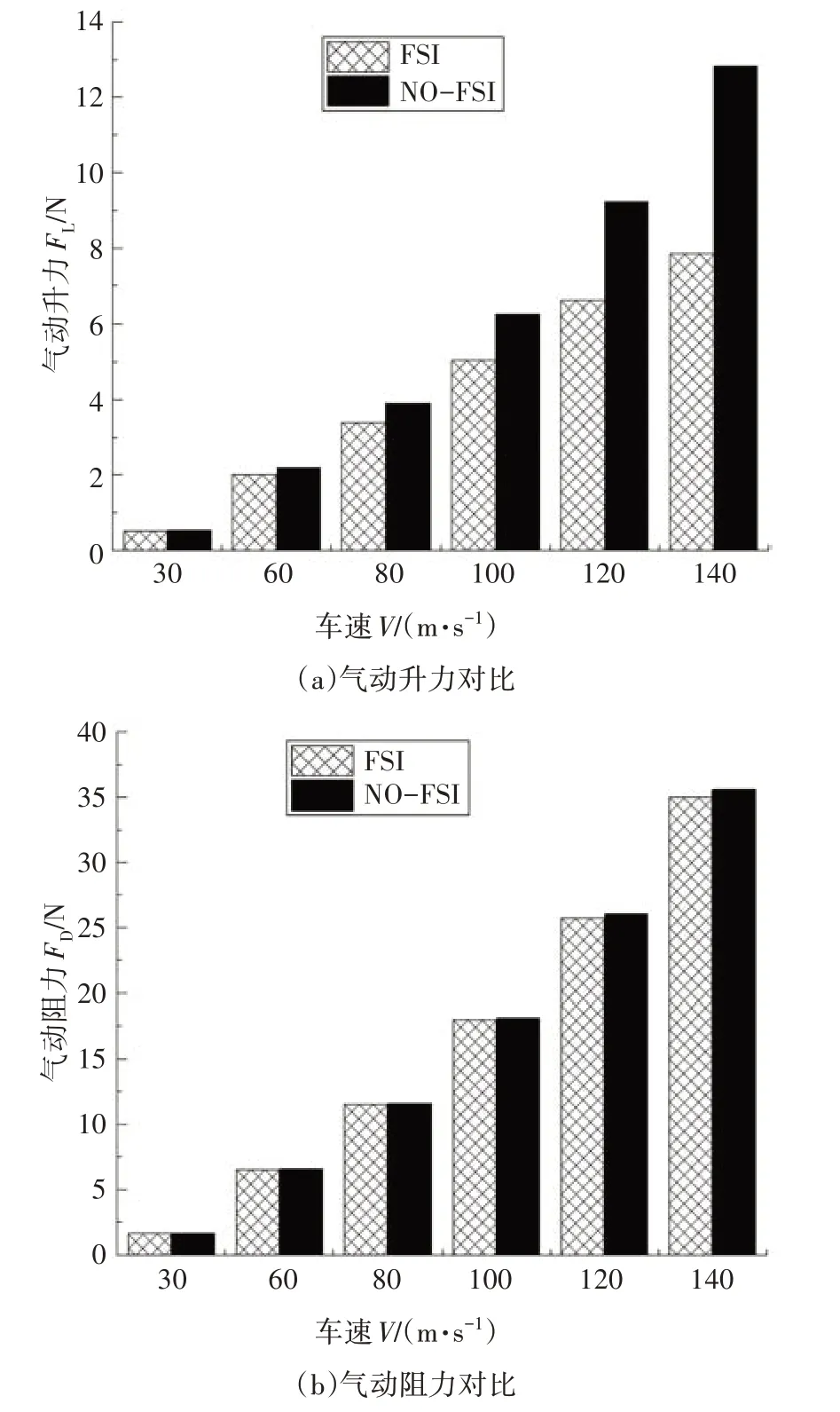
圖4 兩種仿真方法氣動阻力與氣動升力對比圖Fig.4 Comparison of aerodynamic drag and aerodynamic lift between two simulation methods

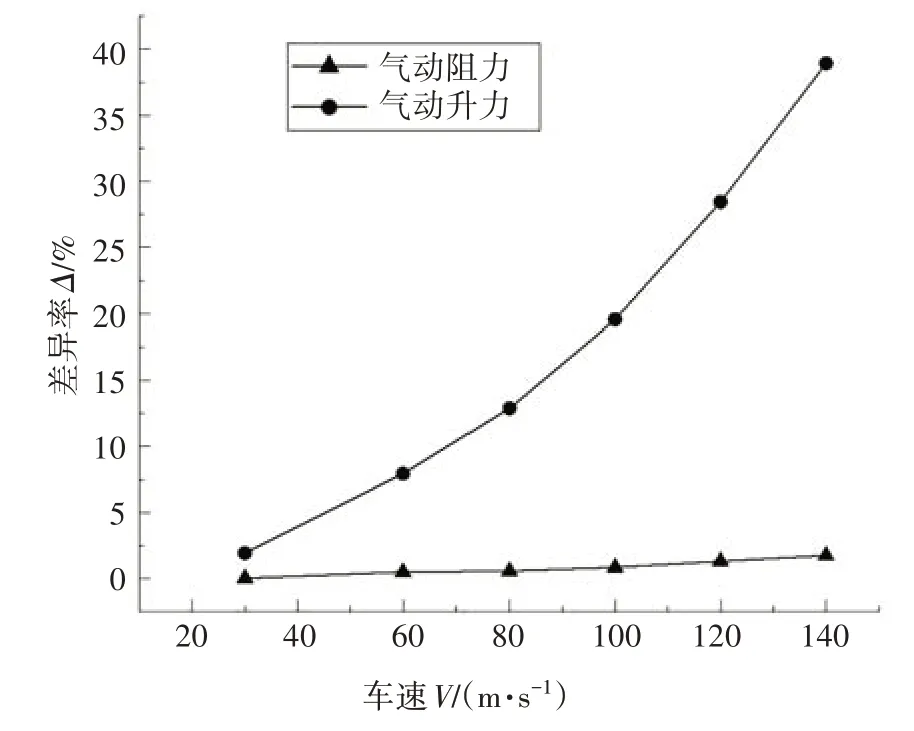
圖5 升力阻力差異率曲線Fig.5 The difference rate curve of lift resistance

圖6 整車升阻力波動情況Fig.6 The fluctuation of the lift and drag of the whole vehicle

在高速工況下，懸架受時變氣動載荷影響以及輪胎行駛過程中發(fā)生形變，進而車輛姿態(tài)改變量變大，改變了車輛周圍外流場結構，氣動力受此影響繼而改變.

由圖4圖5可以看出，是否考慮流固耦合效應對車輛氣動阻力影響較小，不同車速下差異率均在4%以下并且流固耦合數(shù)值仿真阻力值普遍較傳統(tǒng)數(shù)值仿真偏小，相反地，流固耦合對氣動升力的影響較氣動阻力更加嚴重，數(shù)值仿真結果明顯小于傳統(tǒng)CFD數(shù)值仿真，隨車速增大，差異率增大并且都在5%以上，最大可達到38.9%.氣動升力直接影響車輛對地面的附著力，由圖5 圖6 可知，考慮流固耦合效應數(shù)值仿真變化與傳統(tǒng)數(shù)值仿真相比更加劇烈，因此流固耦合CFD 更能真實反映車輛行駛情況，為車輛穩(wěn)定性設計提供參考.

為了更加明顯體現(xiàn)氣動力改變的原因，使用車頭下移到最大時車底部速度矢量來對比分析兩種仿真方法結果，如圖7所示.

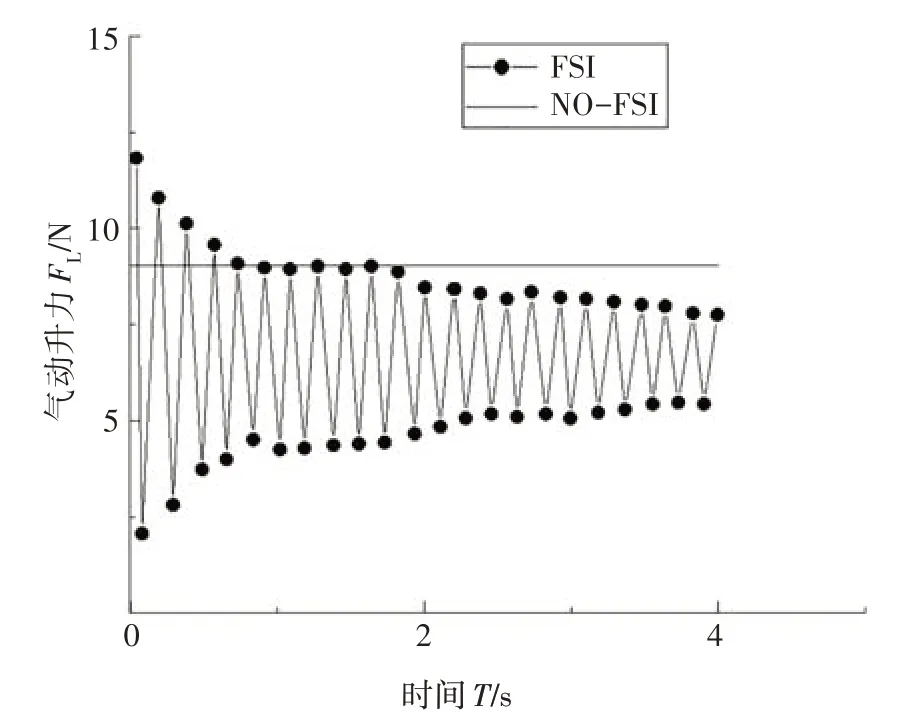
圖7 不同仿真方法升力時域圖（120 km/h）Fig.7 Time-domain diagram of lift for different simulation methods（120 km/h）

傳統(tǒng)CFD 仿真結果車底部流速保持在一個穩(wěn)定的值，而流固耦合CFD 仿真，車底部速度隨時間變化，由圖8 可知，F(xiàn)SI 車底部流速大于傳統(tǒng)仿真流速.由伯努利原理，流速變大導致壓力變小，即為流固耦合仿真升力小于非耦合仿真的原因.

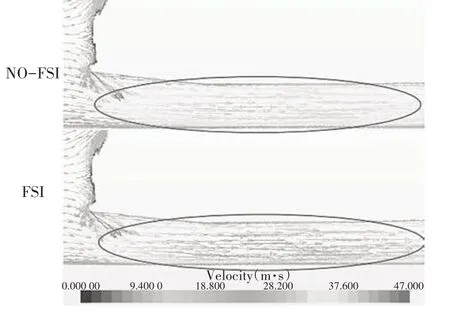
圖8 整車速度矢量圖Fig.8 Vehicle speed vector graph

2.3 風激振特性分析

車身振動屬于流致振動中的風激振，車體在流場中，雷諾數(shù)大于特定值時，會產生周期性的渦脫，作用在車體使其產生振動.主要分析車輛的氣動升力頻譜以及車身振動頻譜.圖9 為車輛氣動升力頻譜分析，圖10為車身振動頻譜分析.

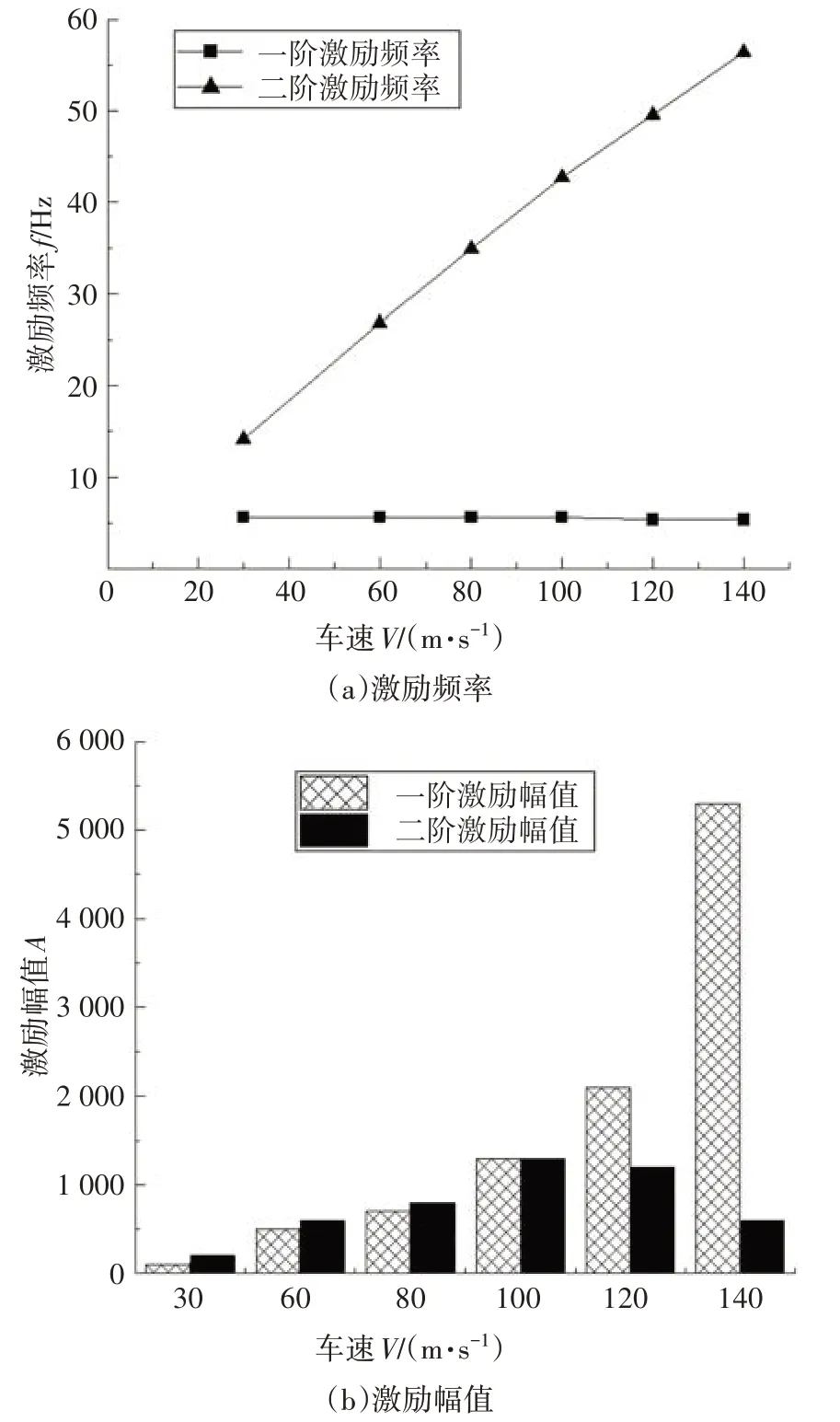
圖9 車輛氣動升力頻譜分析圖Fig.9 Spectrum analysis diagram of vehicle aerodynamic lift

圖10 車輛結構振動頻譜分析圖Fig.10 Vibration spectrum analysis diagram of vehicle structure

由圖9 可知，氣動升力頻譜有兩階頻率，一階為氣動升力與車體的激勵頻率，隨流固耦合效應而發(fā)生改變.車速在100km/h 以上時振動頻率逐漸下降至5.4Hz，其他工況下一階振動頻率基本保持穩(wěn)定在5.6Hz，幅值則隨車速逐漸增加.二階為氣動升力自振頻率，隨車速增加，二階振動幅值先增后減而頻率一直呈現(xiàn)增加的趨勢.

由圖10 可知，整車一階頻率為固有頻率，二階頻率為風激振頻率.對整車進行模態(tài)分析得到車輛振動頻率為4.86 Hz，對比仿真得到的一階頻率4.88 Hz，差別僅為0.4%.可以證明流固耦合仿真方法準確性.車身振動幅值均隨車速增加而增大，一階固有頻率不隨車速變化而改變.對比圖4 圖5、圖9 圖10，當車速較低小于60 km/h 時，氣動升力較小導致流固耦合效應較弱，此時氣動升力體現(xiàn)出自振特性，頻率距離車身一階固有頻率較遠，因此振幅較小.隨著車速提高，氣動升力使車身姿態(tài)改變量增大，流固耦合效應增強，車身振幅增大，該情況下幅值影響因素主要為激勵作用力大小.當速度繼續(xù)增大到100 km/h 以上時，固有頻率與氣動升力頻率接近，升力振幅與車身振幅都迅速增大，因為結構阻尼影響，最終車身振幅達到一定閾值并趨于穩(wěn)定，在此工況下，外界激勵頻率成為決定振幅的主要因素.綜上，如果車輛高速工況下，長時間車身處在強烈振動下，會影響車輛氣動性能和造成部件的疲勞破壞.因此根據(jù)考慮流固耦合效應的數(shù)值仿真方法可以準確獲得車輛各種工況下流致振動情況，為進一步優(yōu)化汽車結構造型方面提供參考.

2.4 汽車風激振的改善措施

車輛風致振動會在一定程度上影響車輛穩(wěn)定性和乘員的舒適性，因此從車輛內部的彈性結構入手，尋找最合適的懸架參數(shù)改善風激振現(xiàn)象.

表1 為人體舒適度與加權加速度均方根aw的評價標準［25］，aw為加權加速度均方根值.

表1 舒適度評價標準Tab.1 Comfort evaluation standard

如圖11所示，當車速小于100 km/h，氣動力耦合效應較弱，人體無不舒適反應，當車速逐漸增大至120 km/h，流固耦合效應增強，車輛與流場產生共振，隨著振動強度的增加，人體不適感也隨之增加.當車速繼續(xù)增加，流固耦合效應更加劇烈，振動強度增加導致人體不適感大幅增加.

圖11 各車速下aw值Fig.11 aw value at different speeds

隨著車輛高速化趨勢發(fā)展，流致振動（風激振）對乘員舒適度和安全性影響越發(fā)增強，因此對此類振動尋找抑制的手段是有必要的.本節(jié)僅考慮懸架彈性剛度的對風激振情況的影響，從而得到不同剛度下的aw值，如圖12所示.

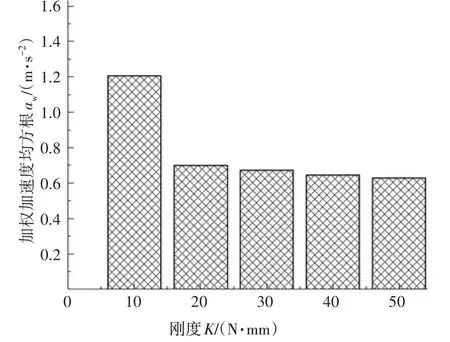
圖12 aw隨懸架剛度K變化趨勢Fig.12 aw changes with suspension stiffness K

由圖12 可知，通過改變彈性元件剛度可有效提高人體舒適度.由于僅考慮了風激振的情況，如果要獲得最佳懸架參數(shù)，需對其他因素（如路面，發(fā)動機激勵）進行綜合考慮.

3 結論

1）流固耦合效應對氣動升力影響嚴重，對氣動阻力影響較小，對二者的影響均隨車速增加而增大.

2）流固耦合數(shù)值仿真對氣動升力的預測更貼近真實情況，可以為車輛的穩(wěn)定性和安全性提供更準確的參考.

3）模態(tài)分析和流固耦合仿真分別得到的車身振動頻率差異率僅為0.4%，證明流固耦合仿真的準確性.影響車身振動的主要因素為外界激勵頻率及作用力大小，獲得各工況下的車輛風激振特性，可以對車身結構進行進一步優(yōu)化設計，依此對振動情況采取改善措施并提高乘員的舒適性.