基于潮流發電與蓄電池充電控制相結合的最大功率跟蹤研究

王世明，董 超

（上海海洋大學 工程學院，上海 201306）

0 引言

當今世界各國對能源匱乏的擔心及對新能源的的研究的重視下,海洋能及其利用技術也在新能源發展的大潮流中作為新能源技術領域中儲量巨大的新生力量也在世界各個國家的重視中取得了前所未有的大發展。現在潮流發電機大多采用直驅式同步發電機,由于是水流直接驅動水輪機帶動發電機發電,中間沒有升速齒輪箱,由于少了中間傳動裝置,所以直驅式的發電方式有更小的傳動損耗,更高的可靠性。

最大功率跟蹤最重要的是控制策略,有根據輸入量發生劇烈變化時的跟蹤算法設計[1,2],有根據實際使用的發電設備類型來設計控制策略[4～9],有根據實際使用的控制電路來設計控制方法的[5],還有根據多種控制方法相結合的算法[3,8]。綜上這些方法幾乎都是直接并網或沒有考慮輸出給誰用的問題,本論文結合爬山搜索法與蓄電池充電方法相結合的控制,從而實現更為簡單的潮流能的利用。

對于雙向直驅式潮流發電機來說,其輸出的電壓及頻率大小易受流速的影響。而且潮流發電不想風力發電那樣在陸地上,潮流發電有的可能在孤島附近遠離電網和用戶,所以這就決定了潮流發電使用方式和風力發電存在不同。接下來將研究潮流發電設備給固定用電設備供電的控制問題,該論文的用電設備選用蓄電池,蓄電池的選擇主要是考慮應用到小型單機發電設備上,及潮流發電的實際使用地方。當發電設備輸出電能經過整流濾波,在經過BUCK-BOOST電壓變換電路獲得幅值滿足要求（蓄電池充電要求）且基本穩定的直流電后給蓄電池充電。

現在,蓄電池充電最常用到的方法是分三個階段充電：預充電（0.1C或0.2C的恒流）,恒流階段,恒壓階段。但由于潮流發電輸出電壓隨流速變化的特點提出一種新的三階段充電方法：預充電（0＜I＜0.2C）,最大功率充電階段,恒壓階段。這樣充電的好處是在保護蓄電池的前提下盡可能的實現潮流發電設備最大功率的輸出。

本文所采用的的最大功率跟蹤控制通過改變BUCKBOOST電路的放大倍數來觀察輸出功率的變化。如果輸出功率變大,那么繼續朝著同樣的方法改變放大倍數,如果輸出功率減小,BUCK-BOOST的放大倍數朝著上次變化的反方向變化。

1 雙向直驅式潮流發電設備的數學模型

1.1 水輪機模型

潮流發電系統的動力來源是捕捉水的動能,根據貝茲證明,水輪機從潮流能中捕獲的功率如式(1)所示：

其中ρ為海水密度,v為流速,A為橫流面積,Cp為潮流能利用系數,該式可以看成：

其中m為單位時間通過橫流面積的海水質量,式(2)所表達的實際物理意義是：水流在流過葉輪的過程中一部分動能被葉輪吸收,一部分繼續以動能的形式保留在水中。

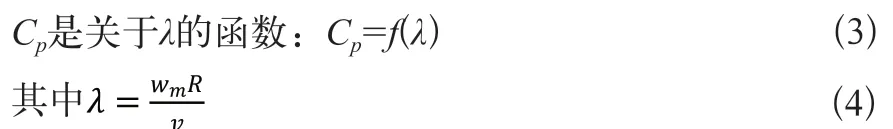
λ為速尖比,wm為葉輪的角速度,R為葉輪半徑,可知wmR為葉尖速度。

根據式(1)～式(4)能夠得出當流速v為某一恒定值時P-wm的關系,如圖1所示。

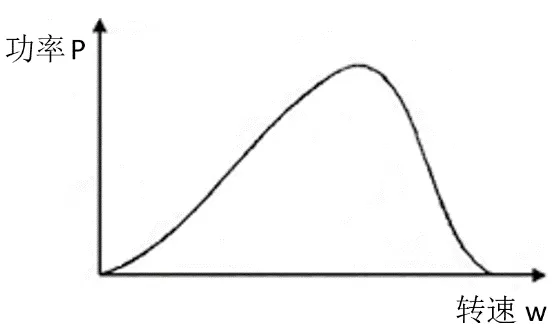
圖1 水輪機某一風速下轉速和輸出功率的關系

水輪機Cp-λ曲線如圖2所示,對一個確定的水輪機時,可以根據式(1)得出功率和的函數關系,從該式能夠看出與的正比例關系即最大時P也最大。關于的關系可由式(3)得出,如圖2所示。從圖2可以看出,當速尖比為λopt時,潮流能利用系數最大為Cpmax。所以,對于一個確定的流速,只有在速尖比為λopt時輸出功率P最大。

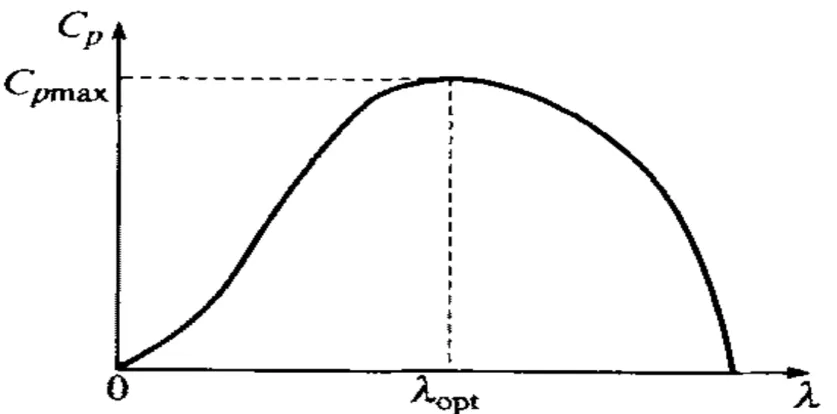
圖2 水輪機 Cp-λ曲線

通過式(1)～式(3)便可得出P-λ的關系記如式(5)所示：

換句話說,當流速改變多少倍水輪機的角速度也得跟著改變多少倍即當：

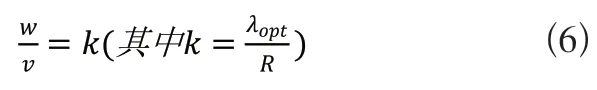
將式(6)代入式(1)得輸出功率最大如式(7)所示：

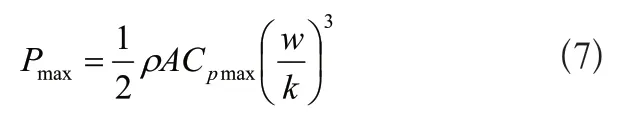
從動力學分析,水輪機另一個重要的物理量為水輪機轉矩：

1.2 發電機模型

為了簡化分析,由于本論文所研究的控制變量不在發電機上,所以將三相交流發電機和后面的整流濾波當做一個整體來分析,發電機模型采用下面公式計算,其中忽略各種損耗。

發電機的感應電動勢公式如式(9)所示：

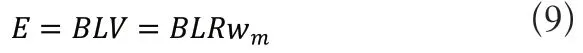
發電機電磁轉矩公式如式(10)所示：

其中B、L為發電機參數,E為發電機感應電動勢,I為發電機輸出電流,R為發電機半徑。

忽略發電機摩擦力,從動力學平衡角度分析如式(11)所示：

J為潮流發電機的轉動慣量；由于從葉輪到發電機沒有變速裝置,所以葉輪和發電機的轉速都為wm。

1.3 蓄電池模型

蓄電池模型采用以下簡化電路模型（一個電阻r和電池VB串聯,其中電池電壓需要實時采集）,如圖3所示。

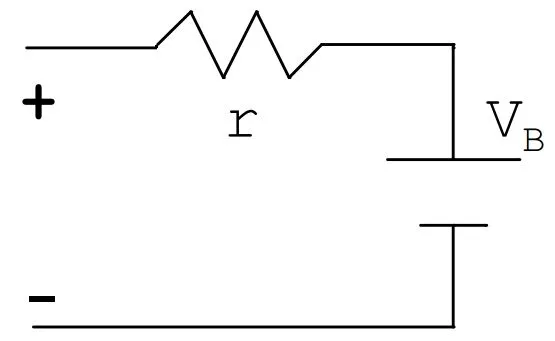
圖3 蓄電池等效電路模型

其中電阻為蓄電池內阻,實際情況中內阻會隨剩余電量的減少而增大,在本論文中為簡化分析蓄電池內阻采用定值來計算。其中電池電壓也會隨蓄電池剩余電量的增加而增加,在本論文中電池電壓通過實施采集蓄電池兩端的電壓代表。

1.4 BUCK-BOOST電路模型

其電壓放大倍數用α表示。

圖4為Buck-Boost電路拓撲,其工作原理：當PWM驅動為高電平時,MOS管T導通,MOS管T與電感L構成回。忽略MOS管的導通壓降,電感上的電流線性增加（電流隨時間增加的斜率,電感中儲存的磁場能增加。當PWM驅動為低電平時,MOS管截止,電感L通過二極管構成回路,電感電流線性減小,電感中儲存的磁場能轉化為電場能。以電感為對象研究伏秒積平衡（左邊電壓為Vin,右邊電壓為Vout）：Vin×ton=Vout×toff（其中ton為MOS管開通時間,toff為MOS管關斷時間）,可知其中D為占空比即,且記

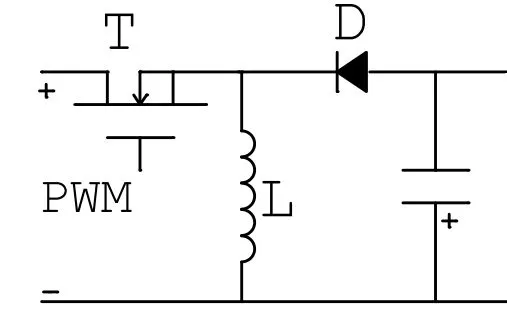
圖4 Buck-Boost電路拓撲

2 最大功率跟蹤原理

根據前面的分析可知,最大功率是能量利用系數Cp的函數,當流速恒定時,潮流能利用系數Cp最大,潮流發電設備獲得能量也就最大。而且,Cp是速尖比的λ函數,當λ最大時Cp也就最大,即當速尖比λ最大時潮流發電機獲得的能量最大。

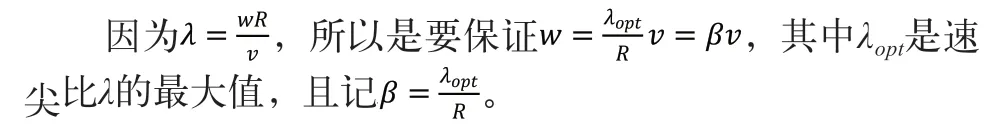
根據前面建立的各個部分的模型可以得到以下的系統模型：

將BUCK-BOOST電路看成是理想的變壓電路,其變壓比記為α。將變壓電路右側的電池的參數歸算到變壓電路左側后,系統的等效電路如圖6所示。

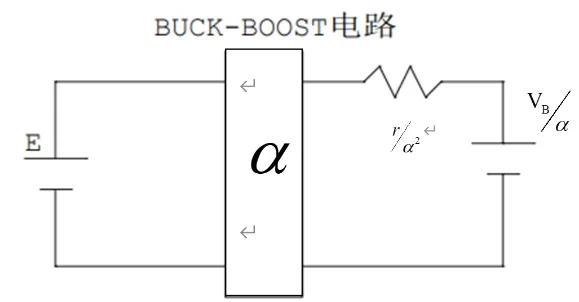
圖6 等效電路

當流速一定時,發電機轉速和變壓電路放大倍數關系通過發電機的動力學分析得發電機因水而獲得的動力轉矩：

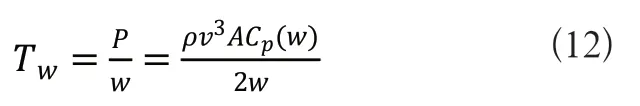
發電機受到的電磁轉矩分析：

假設發電機的轉速為w,由前面介紹的發電機模型可知發電機輸出的電動勢為：

E=BLV=BLRwm,根據系統的等效電路模型可知發電機輸出的電流如式(13)所示：

發電機受到的電磁阻力如式(14)所示：

發電機受到的電磁轉矩可以由式(13)、式(10)聯立得出如式(15)所示：

將式(12)、式(15)聯立：

所以通過流速儀將實施采集到的流速信號反饋到MPPT控制器,輸出的PWM控制信號控制BUCk-BOOST升降壓電路的放大倍數即可完成最大功率的跟蹤。

3 仿真研究

3.1 仿真模型的搭建

為了驗證上述分析的控制策略的有效性,本論文根據下圖所示系統結構圖及上面分析的算法在MATLAB/Simulink中搭建潮流發電系統的仿真。

水輪機采用上面介紹的水輪機模型。葉片半徑：R=0.5m；最佳葉尖速比：λopt=5；最大潮流能利用系數Cpopt=0.4。發電機參數：磁場強度B=10；發電機長度L=0.5m；發電機直徑為0.4m。蓄電池參數：內阻r=1Ω；額定電壓V=24v。

3.2 仿真結果分析

圖8為仿真時流速的階躍流速信號,0～5s流速為4m/s,5s～10s流速為8m/s。

經過對潮流發電設備系統的分析,在理論層面解釋的本論文所提出的控制方法的正確性。并通過在MATLAB/Simulink仿真平臺搭建實驗模型得出了如圖7～圖9所示的仿真結果。從圖7、圖8仿真的結果分析可知,兩圖中存在的過沖和震蕩現象是由于潮流發電設備的轉動慣量決定的,根據經典控制理論可知：轉動慣量越大震蕩和過沖所經歷的時間也會越長。從上面的仿真結果可以看出,本論文所提出的根據對BUCK-BOOST電路的電壓放大倍數的控制能夠實現最大功率的跟蹤。

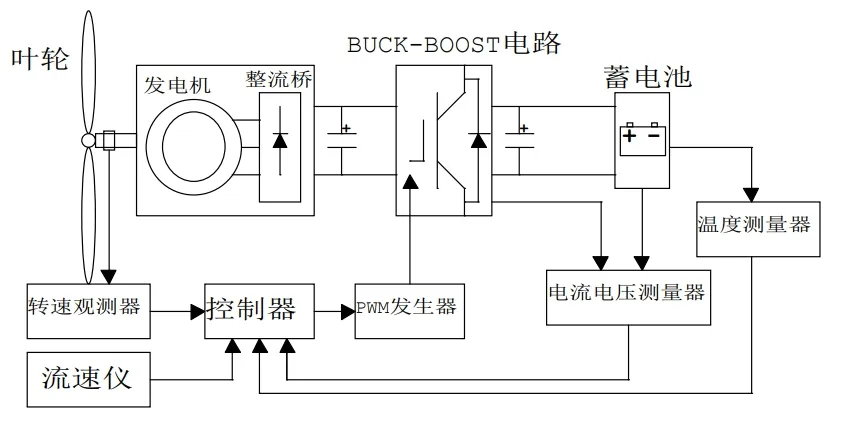
圖7 系統主電路及其控制策略

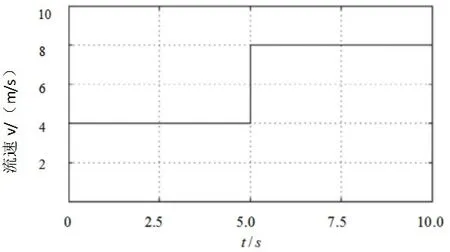
圖8 流速階躍變化示意圖

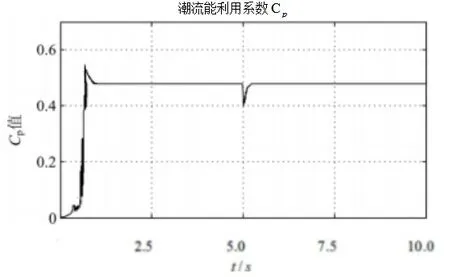
圖9 潮流能利用系數變化曲線

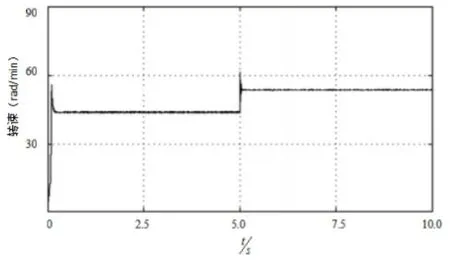
圖10 發電機轉速曲線

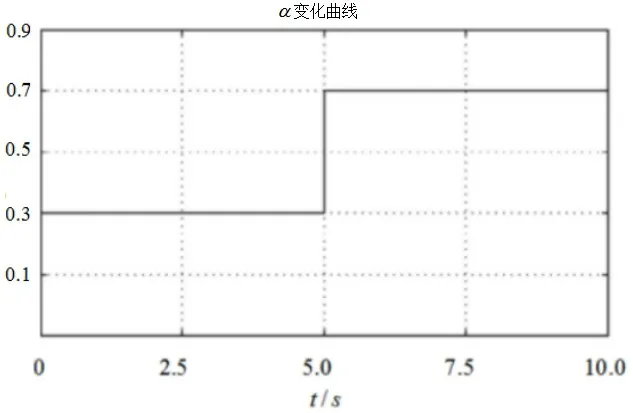
圖11 α的變化曲線

4 結語

本論文所提出的最大功率跟蹤控制策略是通過對BUCK-BOOST電路中開關器件BJT的占空比的調節來實現的。該論文的控制通過對流速的測量作為該系統的輸入,然后通過已知的系統最優速尖比來達到對開關電路的占空比進行控制,從而實現最大功率跟蹤的目標。

該系統在實現最大功率跟蹤的同時也改善了系統的動態特行,因為根據上面分析的流速和α的關系可以得出流速變化的大小決定α的大小即流速變化越大那么α的變化也就越大,再根據α與系統轉矩的關系可知兩者正相關,所以該控制方法能夠改善潮流發電系統的動態性能即縮短動態的時間,這樣就減小的后面電路對穩壓的要求。