基于極值搜索算法的液壓蝶閥系統PIλDμ參數整定

吳繼偉，于春梅

（1.西南科技大學 信息工程學院，綿陽 621010；2.特殊環境機器人技術四川省重點實驗室，綿陽 621000）

0 引言

液壓蝶閥系統具有啟閉扭矩大、壓力損失-小、響應速度快等特點,被廣泛應用于航空航天、工農業生產等各個領域[1,2]。實現該系統的快速控制具有十分重要的意義。

經典的PID控制方法結構簡單、控制靈活,在液壓蝶閥控制系統中被廣泛使用[3]。但是液壓蝶閥系統結構及組成極其復雜,是一個強非線性系統,傳統的PID控制方法無法較好的完成液壓蝶閥的控制。分數階將分數階微積分理論與PID控制方法結合,能夠使控制系統獲得更好的動態響應特性。文獻[4]將分數階PIλDμ引入地鐵列車的速度控制,研究結果表明分數階PIλDμ控制算法,可以使列車實現更優的速度控制和穩定性。文獻[5]針對智能車高速行駛下對目標軌跡的快速跟蹤要求,設計了分數階PIλDμ控制器,仿真結果表明分數階PIλDμ控制器具有比傳統PID控制器更好的動態性能。

相比于傳統PID控制方法,分數階PIλDμ比整數階PID控制器多了兩個可調參數,使得分數階PIλDμ控制器的參數整定變的更加復雜。對此,文獻[6]采用遺傳算法整定分數階參數,仿真結果表明該方法能夠完成分數階PIλDμ參數的在線整定。但遺傳算法計算復雜,難以處理其中非線性約束條件。文獻[7]設計了一種基于神經網絡的分數階PIλDμ控制器,經過仿真驗證,神經網絡分數階PIλDμ能夠較好完成其參數的整定,但是神經網絡算法對樣本需求量大,而且對樣本質量要求高,局限性比較明顯。極值搜索算法是一種簡單、高效、不基于模型的自適應算法,只需通過被控對象的輸入輸出,即可實時搜尋被控對象輸出的極大、極小值。本文將極值搜索算法與分數階PIλDμ相結合,提出了一種基于極值搜索算法的PIλDμ參數整定方法。同時,為了更好地驗證該算法的有效性,結合ADAMS、UG、AMEsim三種軟件對液壓蝶閥控制系統進行建模。AMEsim和MATLAB/Simulink聯合仿真結果驗證了本文的有效性。

1 極值搜索算法

極值搜索算法是由Tsien教授于1954年提出的一種自適應控制方法[8],能夠在某些信息未知的情況下根據輸出、能耗等條件使系統獲得滿意控制效果。其中基于擾動的極值搜索算法是極值搜索算法中常用的一種控制方法,該方法只需要根據系統的擾動以及合適的濾波器就可以獲得系統梯度信息[9]。以基于攝動的單變量極值搜索算法為例。

圖1為基于攝動的極值搜索算法原理圖。算法的目的是調節θ使得f(θ)取極小值。算法通過探測信號的擾動獲取目標函數的梯度信息,并沿著負梯度方向進行搜索,尋找目標函數的極值。然后根據該梯度信號對控制器參數的最優值不斷進行在線搜索[10]。

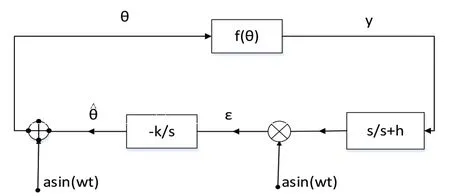
圖1 基于攝動的極值搜索算法原理圖

假設目標函數f(θ)具有如式(1)的二次形式：

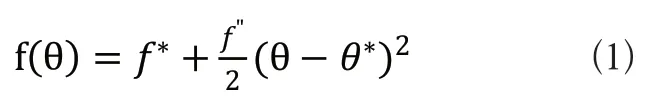
其中f(θ)是需要極小化的輸出：f*為需要搜索的最小值,f"為函數f(θ)的二階微分。θ*為使得f(θ)達到最小的最優參數；θ是實際輸入參數；k是調節積分環節的自適應增益；a是探測信號的幅值；ω為探測信號的頻率；為高通濾波器。

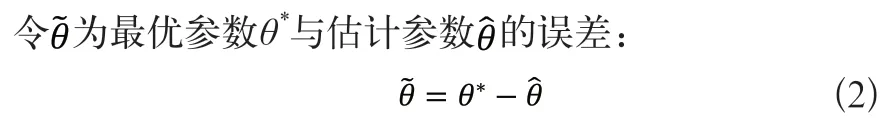
將輸入參數代入式(6)：

利用基本的三角恒等關系展開式(4)得到：

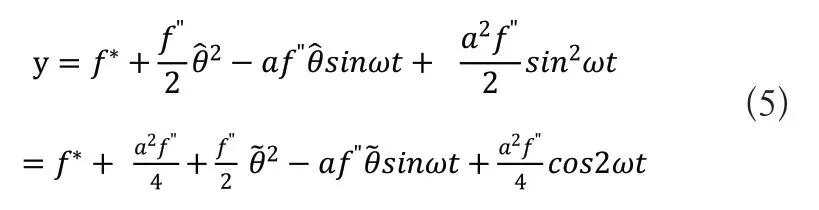
經過高通濾波器,濾除直流信號可得f*可得：

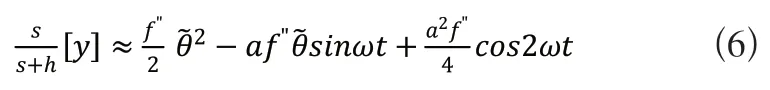
加入乘法信號sinωt得到：

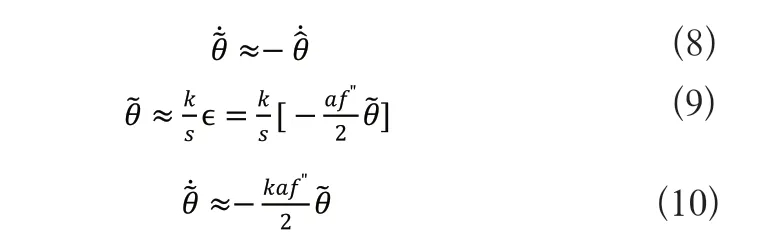
由式(10)可知,當選擇適當的增益k和振幅a,隨著迭代次數的增加,極值搜索算法會使輸入信號與最優輸入的估計誤差逐漸衰減到0。

2 控制器設計與系統建模

2.1 基于極值搜索算法的PIλDμ參數整定方法

分數階PIλDμ將傳統的PIλDμ法擴展到分數階領域[11]。與傳統的PID方法相比,該方法新增了積分階次λ、微分階次μ兩個參數,使其有更大的參數調節范圍,擁有比傳統PID更好的控制效果。但是分數階PIλDμ參數整定比較困難。因此,本文將極值搜索算法與分數階PIλDμ控制算法相結合,利用極值搜索算法在線調整PID控制器參數,使整個系統跟蹤誤差最小,圖2是基于極值搜索算法的參數整定方法原理框圖。使用誤差平方積分準則函數ISE為目標函數J(θ)[12]。

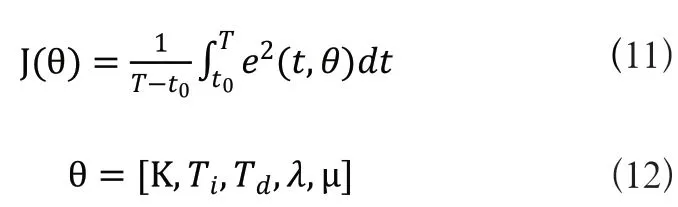
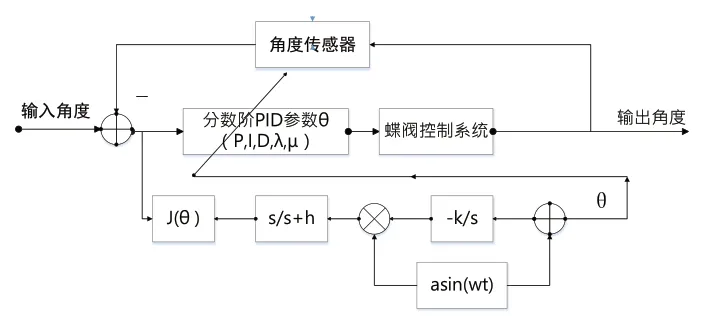
圖2 基于極值搜索算法的PIλDμ參數整定方法原理框圖

其中e為閉環輸入與輸出的誤差,θ為分數階PIλDμ控制參數。通過極值搜索算法的極值尋優能力,在線調整分數階PIλDμ參數,使目標函數J(θ)達到最小值。完成分數階PIλDμ參數的自整定。

2.2 系統建模

液壓蝶閥系統控制框圖如圖3所示,整個系統由液壓伺服執行器、蝶閥及傳動機構組成。

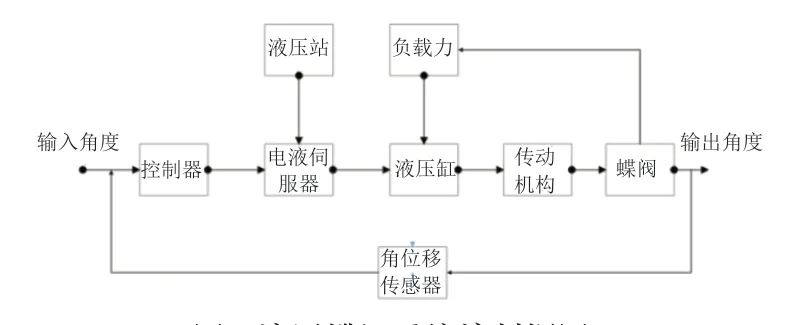
圖3 液壓蝶閥系統控制框圖

該系統的傳動機構為曲柄連桿式裝置,該裝置可以得到更好的角度控制精度,但是會導致整個傳動機構運動軌跡及受力情況變得十分復雜,常規的數學分析方法難以分析整個傳動過程。針對這一問題,本文首先利用UG軟件建立各零件模型,根據實物模型組裝成裝配體,如圖4所示。

圖4 傳動機構及蝶閥三維模型

然后將UG軟件建立的模型以.xt格式導出。使用ADAMS軟件對該模型進行仿真分析,得到系統中液壓桿的伸長量與蝶閥轉動角度和液壓桿受力相關數據,使用最小二乘的方法完成數據的擬合。得到液壓桿伸長量與蝶閥轉動角度關系曲線、液壓桿伸長量與液壓桿受力關系曲線,如圖5、圖6所示。

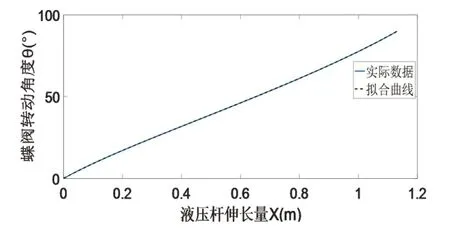
圖5 液壓桿伸長量與液壓桿受力關系曲線

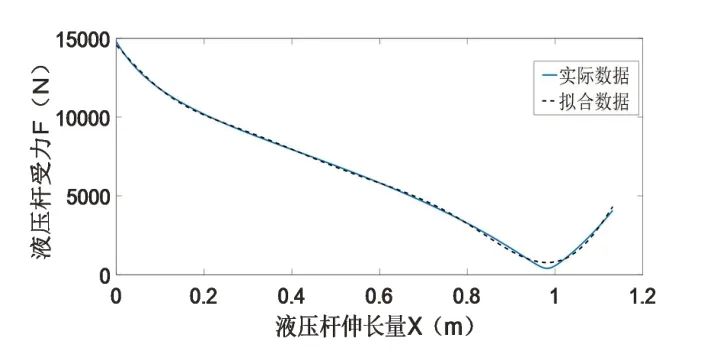
圖6 液壓桿伸長量與蝶閥轉動角度關系曲線

最后通過對整個液壓伺服系統的分析,利用AMEsim軟件建立了電液伺服系統所有重要部件模型,如油箱、電機、電磁溢流閥、電液伺服閥、液壓缸等部件。加入傳動機構數據完成整個液壓蝶閥控制系統模型的建立。圖7為AMEsim-Simulink聯合仿真中電液伺服系統AMEsim模型。

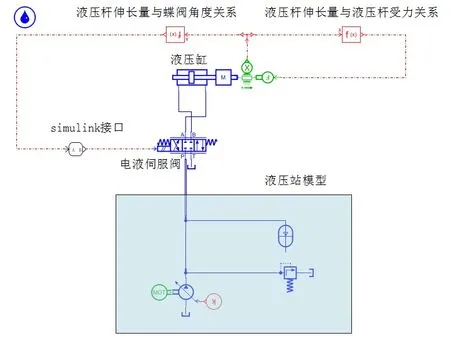
圖7 電液伺服系統AMEsim模型

2.3 AMEsim-Simulink聯合仿真

AMEsim軟件可以建立更加精確的液壓伺服系統模型,在MATLAB軟件中更適合控制算法的設計與仿真。利用AMEsim和Simulink的聯合仿真技術可以充分發揮兩種軟件的優勢[15]。本文在AMEsim軟件中建立液壓伺服系統模型,在MATLAB軟件中完成基于極值搜索算法的分數階PIλDμ參數整定方法的設計。通過S-function接口將兩個軟件聯合在一起,完成整個控制系統的設計與仿真。

3 實驗結果分析

3.1 基于極值搜索算法的PIλDμ參數整定

首先將本文分數階PIλDμ參數整定方法中θ參數λ、μ設置為定值1,利用極值搜索算法只整定PID的三個參數值。其目標函數J(θ)及PID參數整定曲線如圖8、圖9所示,從圖中可以看出PID三個參數在經過3.7秒后從0逐漸穩定到12、0.07、0.6左右。同時目標函數J(θ)隨著PID參數的整定最終趨于0值。圖10是系統階躍響應圖,由圖可知,PID控制方法在經過極值搜索算法在線整定參數后能較好的完成液壓蝶閥系統的控制。

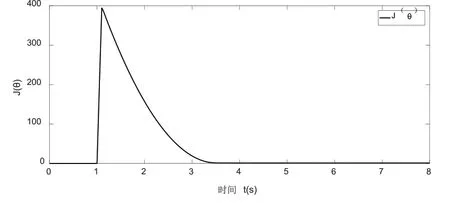
圖8 目標函數J(θ)

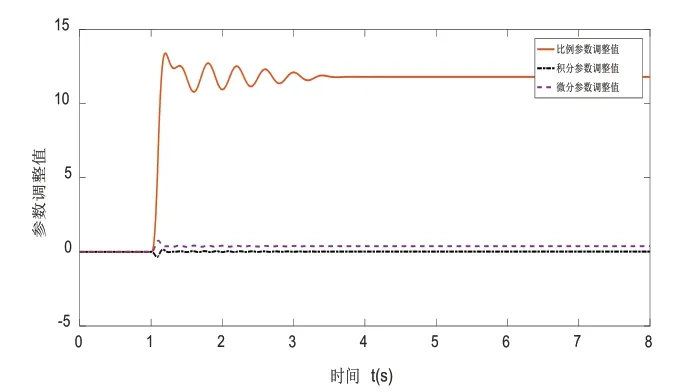
圖9 PID參數整定曲線

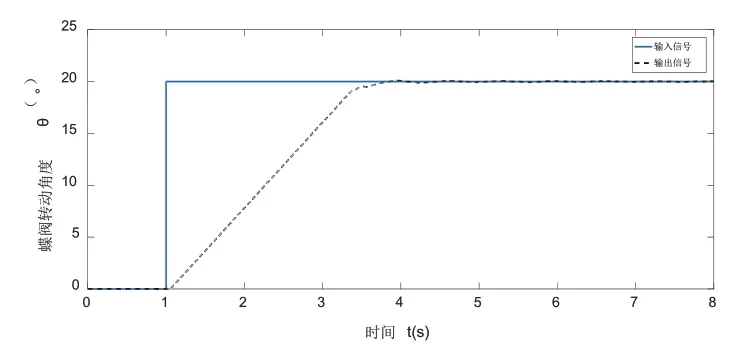
圖10 系統階躍響應

3.2 基于極值搜索算法的分數階PID參數整定

使用極值搜索算法整定分數階PIλDμ參數,從圖11中可以看出分數階PIλDμ參數P、I、D、λ、μ五個參數在3.4秒后分別整定到11.2、3.3、0.08、0.4、1左右。由圖12可知,其目標函數J(θ)也最終收斂到0值附近。圖13顯示出參數調整后的分數階PIλDμ具有較好的控制效果。

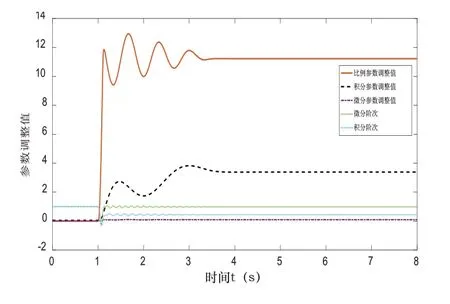
圖11 PIλDμ參數整定曲線

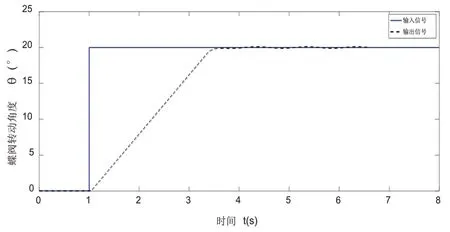
圖12 系統階躍響應

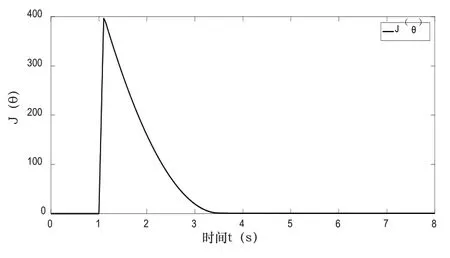
圖13 目標函數J(θ)

3.3 不同控制方法的控制效果比較

為了研究分數階PIλDμ與傳統PID控制效果的區別和極值搜索算法參數整定與參數優化能力,本文將通過經驗調整參數的PID、基于極值搜索算法的PID、基于極值搜索算法的分數階PIλDμ、初始化參數的極值搜索PID、初始化參數的極值搜索分數階的控制效果作對比。不同控制方法的控制效果如圖14所示。

從圖14中可以看出,通過經驗調整參數的PID控制效果十分不理想,跟蹤速度慢且存在超調。將極值搜索算法應用于PID、分數階PIλDμ參數調整中,可以看到其控制效果有了明顯的提升。分數階PIλDμ比普通PID多了兩個參數,從圖14中可以看出分數階PID比普通PID具有更好的控制效果。

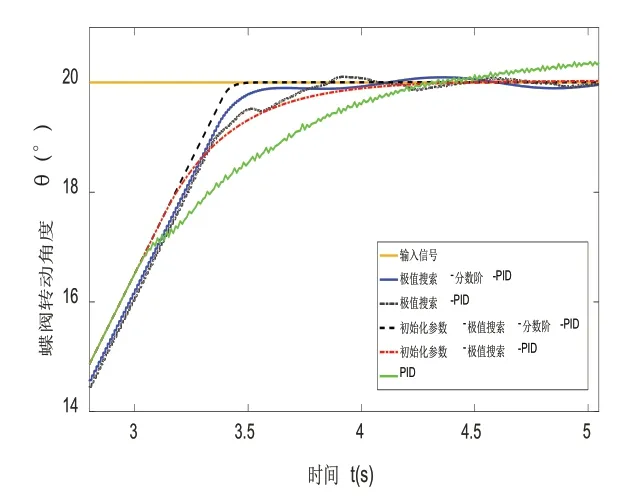
圖14 不同控制方法控制效果局部放大圖

由于極值搜索算法參數是從零開始整定的,其整定過程需要較長的時間。從圖14可以看出,相比于通過經驗調整參數的PID,基于極值搜索算法的PID、分數階控制效果曲線會有一定的滯后。將通過經驗調整的PID參數初始化于極值搜索算法中,從圖14中可以看出初始化參數的極值搜索PID、分數階PIλDμ具有更好的控制效果,驗證了極值搜索算法的參數尋優能力。

在實際工作情況中,閥門需按照給定的斜坡信號動作。因此這里將輸入設定為斜坡信號,從圖15中可以看出基于極值搜索算法的分數階PIλDμ控制方法能夠較好的完成液壓蝶閥控制系統動作要求。

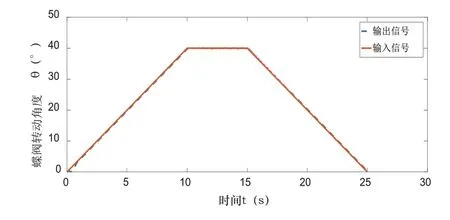
圖15 斜坡信號跟蹤圖

4 結語

本文將分數階PIλDμ控制方法運用于液壓蝶閥控制系統中,并利用極值搜索算法對其參數進行整定,同時,為了更好地驗證算法的有效性,結合三種軟件建立了液壓蝶閥控制系統的仿真模型。經仿真驗證,極值搜索算法能較好的完成PID、分數階PIλDμ的參數整定與參數尋優。相比于傳統PID算法,基于極值搜索算法的分數階PIλDμ能更好的完成液壓蝶閥系統的控制。