基于多目標優化的中繼衛星重調度方法

龍運軍，李恒偉，尹 謙，郭 磊

(1.北京空間信息中繼傳輸技術研究中心，北京 100094；2.中南大學 交通運輸工程學院，湖南 長沙 410075)

0 引言

隨著衛星數量增多，航天器之間的數據交流需求越來越大，對中繼衛星的需求也變大。中繼衛星的運行軌道在地面36 000 km之上，軌道高度高，覆蓋面廣。3顆中繼衛星組成的衛星網絡，能全部覆蓋300～2 000 km軌道上的衛星，實現數據中繼和對衛星的連續跟蹤，使得衛星數據傳輸對地面測控站的依賴減小，節省衛星數據傳輸的成本。

隨著對中繼衛星的需求增大，如何合理地調配中繼衛星資源，滿足用戶的需求，成為提高整個系統利用效率的關鍵。當前，對中繼衛星的調度方法研究大多是在特定的理想情況下，對于單目標需求進行優化。

現有中繼衛星系統調度研究主要分為對應用模式的研究和對算法的研究。在應用模式方面，Hajghassem[1]對NASA的中繼衛星系統在航天網絡的應用模式進行了分析。Reddy[2]針對單窗口和單根天線的約束調度問題進行了求解，提出的動態算法能夠在約束條件下獲得優化結果。Rojanasoonthon[3]針對多時間窗口和多址鏈路約束調度進行求解，采用了分支定界法來進行最優解的求解。

在算法方面，顧中舜[4]將蟻群算法運用到調度問題中，與經典的遺傳算法和模擬退火算法進行比較，發現蟻群算法更適合中繼衛星調度問題，無論是時間還是精度都更優。Liu等[5]利用時間窗口的靈活范圍和數學特征，提出了一種調度算法，與其他經典算法對比，提高了約11%的任務完成率。He等[6]基于中繼衛星動態調度中的多址問題，構建了一種基于隨機優化的數學架構，將問題轉化為一個天線內嵌多個的形式，并利用了2種算法進行求解。張彥等[7]主要針對新增任務和任務時間變化等動態擾動建立了中繼衛星動態調度模型，并提出了動態擴展/刪除樹搜索算法，以刪除任務和調整任務之比作為指導，提高了算法效率，并證明了其能夠在實際中運用。

上述研究主要側重于中繼衛星系統靜態任務調度。隨著中繼衛星的運用范圍越來越大，各類型用戶目標對中繼衛星系統資源需求動態性越來越高，而且在未來戰爭中，中繼衛星系統作為重要戰略資源是敵人破壞摧毀的目標。面對海量應急中繼使用需求或資源受損時，如何快速重新進行資源分配調整計劃，成為發揮或保持整個中繼衛星系統效能的關鍵。當前研究對中繼衛星的調度方法大多是針對單目標需求進行優化，如最大化任務完成度，對于多目標情況的研究鮮有涉及。

因此，本文針對中繼衛星系統接收海量臨時申請或者中繼資源故障時如何快速進行重調度問題進行研究，以滿足最大化任務完成率和最小化動態擾動測度2個互相沖突的需求為優化目標，建立了調度過程中突發新增任務的動態調度的模型，基于NSGA-Ⅱ多目標優化算法，對中繼衛星進行動態重調度。

1 中繼衛星應用模式

1.1 系統工作原理和流程

中繼衛星系統是指將中繼衛星發射至地球的靜止軌道，并將地面站作為終端，對中低軌道衛星進行大面積覆蓋，提供測控通信和數據中繼的系統。

中繼衛星系統概貌如圖1所示，可以將整個中繼衛星系統分為3個部分：第1部分是中繼衛星；第2部分是用戶層，由多種用戶航天器構成；第3部分為地面設施，主要包含用戶航天器及中繼衛星的管理中心和地面網絡終端。

圖1 中繼衛星系統概貌Fig.1 Overview of relay satellite system

由于用戶層與地面可見時間較短，需要利用中繼衛星進行數據中轉，在用戶航天器與中繼衛星的可見時間窗口內，將需要傳給地面的數據信息傳給中繼衛星。用戶航天器管理部門需要根據中繼衛星管理部門對外發布的下一周期衛星資源，以及自身的任務需求，向中繼衛星的管理部門提交任務申請，中繼衛星管理部門對用戶需求進行整理，科學合理地分配有限的衛星資源，并生成調度方案。對于突發情況，中繼衛星管理部門會及時啟用相應的動態調度算法進行調整，保證中繼衛星服務的正常運行，并獲得動態調度方案。最后，各部門依據最終方案，完成地面站和用戶航天器之間的數據傳輸任務。

1.2 系統應用模式分析

本文的中繼衛星系統應用模式采用傳統的通用模式，可歸納如下[8-10]：

① 用戶管理部門提交的任務申請信息包括其任務的緊急程度、需求的服務時間和窗口等。提交的每一項任務只能所屬一個用戶航天器，通常對應一個或多個中繼衛星服務時間窗口，任務必須一次性完成。

② 在用戶申請完畢后，由中繼衛星管理部門進行統計，并通過靜態調度算法，根據用戶需求生成合理的衛星調度方案，依據調度方案完成任務。

③ 對于在中繼衛星執行任務過程中可能出現的動態擾動，如緊急新增任務、資源失效等任務變化，導致靜態調度方案中部分任務可能無法按原有方案進行執行時，需要緊急啟用動態調度算法，進行動態調度，來滿足任務需求；失效資源上已安排的任務均作為新增任務申請進行重新分配。

④ 在靜態調度方案和動態方案生成完畢后，獲得一個新的方案，中繼衛星將按新的方案執行任務。同時，中繼衛星管理部門需要將任務執行情況下達至各個用戶及所對應的地面站。

2 考慮任務擾動的中繼衛星重調度模型

中繼衛星系統調度問題復雜，涉及變量眾多，約束條件繁雜，因此本文在構建模型時做了適當簡化，降低求解難度。

2.1 問題假設

為降低問題建模與求解難度，對中繼衛星任務調度問題做了簡化，做如下基本假設[11-13]：

① 不考慮不同任務間可能存在的相關性；

② 所有任務被執行時必須一次性完成；

③ 用戶申請的服務時間窗口為固定的時間窗口，不具備彈性。

2.2 變量符號說明

本文構建的中繼衛星重調度模型將要用到的變量定義如表1所示。

表1 符號定義Tab.1 Symbol definition

2.3 模型決策變量和優化目標

2.3.1 決策變量

在本文選定的應用模式下，整個問題實際上就是對用戶申請的任務確定6個要素的信息：任務的執行緊急程度、任務執行的最早開始時間和最晚結束時間、任務的執行所需時間、任務能被執行的天線和任務對應用戶航天器。故模型的決策變量為xtrj,actstrj和acdtrj。

決策變量xtrj的值只有0或1兩種，用來表示任務是否被成功執行，成功其值為1，不成功則為0。決策變量actstrj表示在可見窗口j內，任務t在被資源r執行的開始時間，為一個連續變量。決策變量acdtrj，表示在可見窗口j內，任務t在被資源r執行的實際持續時間，為一個連續變量。

2.3.2 優化目標

在中繼衛星重調度模型中，選取最大化任務執行率和最小化動態擾動測度為目標函數。最大化任務完成率是指算法求解時，在滿足約束條件的情況下，向任務完成率最大的解靠近。

動態擾動測度(DDM)是指當動態擾度發生后，經過算法產生的動態調度方案與之前靜態調度的方案的差異程度[14]：

ψ(s0,snew)=λdelndel+λcnc，

(1)

式中，s0表示靜態調度的方案；snew表示動態調度后產生的新方案；ndel表示從靜態至動態調度刪除的任務與除新增任務外另增加的任務數量之和；nc表示從靜態調度到動態調度的任務調整數量(比如任務從第1個衛星調整到第2個衛星執行)數量；λ表示任務的權重。重調度的目標函數為：

(2)

minf2=λdelndel+λcnc。

(3)

本文建立的中繼衛星重調度模型中，將最大化任務完成率作為本文的優化目標，即希望通過算法求解時，在滿足約束條件的情況下，向任務完成率最大的解靠近。

2.4 約束條件

在中繼衛星系統調度問題中，主要涉及兩方面約束：一方面為資源約束；另一方面為任務需求約束。

2.4.1 資源約束

資源約束包括可見時間窗口約束和資源的使用約束。

① 可見時間窗口約束

中繼衛星與用戶航天器之間可以傳輸數據的時間稱為可見時間窗口，要求在任務被執行的過程中，必須與其所屬的用戶航天器對應的與中繼衛星的可見時間窗口匹配。由此可得約束條件C1,C2：

(4)

(5)

C1表示任務執行的開始時間不能小于其所屬的用戶航天器與中繼衛星的可見時間窗口的開始時間。C2表示任務執行的結束時間不能大于其所屬的用戶航天器與中繼衛星的可見時間窗口的結束時間。

② 天線資源約束

在中繼衛星重調度問題中，一個天線資源在任意時刻只能執行一個任務，得到約束C3：

C3:(adjust+Dmr+rec)∩(adjust+Dnr+rec)=φ,

?t∈T,r∈R,m∈T。

(6)

2.4.2 任務需求約束

任務方面的約束包括任務執行時間約束和任務執行約束。

① 任務服務時長約束

在中繼衛星重調度問題中，任務在被調度時，分配的任務時長必須等于任務需求的服務時長，可得約束C4：

(7)

② 任務時間窗口約束

與可見時間窗口相似，任務不是時時都能夠被執行，每個任務都有一個能被執行的窗口，稱為服務時間窗口，因此任務的執行時間都應在任務服務時間窗口內。可得約束C5,C6：

(8)

(9)

C5表示任務的執行時刻應遲于其對應的服務時間窗口的開始時間。C6表示任務的執行結束時刻應早于其對應的服務時間窗口的結束時刻。

③ 任務執行約束

在中繼衛星重調度問題中，中繼衛星執行的任務只能被一個天線選擇執行，同時也只能選擇一個可見時間窗口被執行，可得約束C7,C8：

(10)

(11)

2.5 重調度數學模型

本文所構建的中繼衛星多目標重調度模型以任務完成率最大化和動態擾動測度最小化為目標，以資源和任務需求為約束，構建的具體數學模型如下：

minf2=λdelndel+λcnc，

3 基于多目標優化的重調度算法

本文研究的內容為多目標優化下的中繼衛星的重調度。基于多目標優化，選取NSGA-Ⅱ這一多目標優化領域內的流行算法作為本文動態調度問題的優化算法，探究其對中繼衛星動態調度的優化效果。

3.1 算法簡介

NSGA-Ⅱ作為優化算法的一種，基于遺傳算法改進而來。遺傳算法作為經典的智能優化算法，是以達爾文生物學中“優勝劣汰”為背景，以自然選擇和遺傳作為原理，模擬生物進化的一種算法。NSGA-Ⅱ算法繼承了遺傳算法優勝劣汰的思想，同時引進了Pareto支配關系和非支配排序、種群擁擠度和精英保留策略等思想[15]。Pareto支配關系和非支配排序主要是為多目標優化服務，種群擁擠度的提出是為了得到最優解在空間中形成均勻的分布，精英保留策略則是為了更方便地選擇出更為優秀的個體，遺傳至下一代。

3.2 流程設計

① 生成靜態調度方案

首先，根據用戶提交的任務信息和中繼衛星資源信息，利用靜態調度算法生成初始的靜態調度方案。主要是通過任務的服務窗口和中繼衛星與用戶航天器的可見時間窗口的交集生成任務的可用時間，運用算法進行初步的任務調度，得到靜態調度方案，方便后續動態擾度測定計算。

② 對第一代種群進行非支配排序

靜態調度后進行動態調度初始方案的生成。在動態調度中，要保證新增任務必須執行，然后考慮執行新增任務后，資源和任務的匹配生成動態調度的初始解，即整個進化算法的初始種群。然后計算種群中每個個體的目標函數值，本文考慮的多目標為最大化任務完成率和最小化動態擾動測度，依據多目標函數值，對每個個體進行非支配排序。

③ 選擇、交叉、變異

選擇是指從父代中選出優秀的個體，進行交配產生下一代。在遺傳算法中選擇的方式有很多，如輪盤賭和錦標賽選擇法等。NSGA-Ⅱ中運用的錦標賽選擇法，即從種群N個個體中，選出k個個體，一般取N的一半，然后根據個體的適應度(Pareto等級和擁擠度)，將表現最好的個體放入交配集。

交叉之前進行編碼，將每個任務和執行任務的衛星都用二進制的方式表達出來。染色體編碼示意如圖2所示。

將所有的任務編碼完畢后，一個任務及其執行情況將會對應一段同樣長度的編碼，然后進行交叉，產生新的2段不同的編碼，本文選用兩點交叉法，實現過程不復雜，也有較好的隨機性。兩點交叉法示意如圖3所示。

圖3 兩點交叉法示意Fig.3 Schematic diagram of two-point crossover method

④ 精英選擇

將輸出的子代與父代合并為同一個種群，計算種群中每個個體的目標函數值，即最大化任務完成率和最小化動態擾動測度，依據多目標函數值，對每個個體進行非支配排序，然后對恰好無法全部放入種群的那層Pareto層級個體進行擁擠度計算，保留擁擠度較大的個體進入下一代。精英選擇示意如圖4所示。

圖4 精英選擇示意Fig.4 Schematic diagram of elite selection

⑤ 算法結束

將上面的4個步驟循環一次，代表整個種群進化了一次，持續循環直到滿足輸出條件，得到最后的優化結果，即重調度的最終結果。

4 仿真實驗和結果分析

4.1 任務需求信息

① 任務編號

在實驗中，為了方便，任務直接從1開始編號。

② 任務對應航天器

任務實際能夠被執行的時間，實際上為任務對應航天器和中繼衛星的可見時間窗口和任務的執行時間窗口的交集。每一個任務相應地對應一個航天器，在本文的實驗中，采用均勻生成隨機數的方法，將任務與航天器一一匹配。

ust=ceil(λ*us)，

(12)

式中，ust表示任務的航天器編號；ceil表示向上取整；λ表示(0，1)的隨機數；us表示每個實驗中用戶航天器的數量。

③ 任務服務時間

由用戶提交任務能夠被執行的開始時間和結束時間。在本文的仿真實驗中，通過隨機數和正態分布來生成。

stst=λ*86 400，

(13)

stet=stst+abs(normrnd(mean,std))，

(14)

式中，stst表示開始時間；stet表示結束時間；mean表示整個服務時間正態分布的均值；std表示整個服務時間正態分布的標準差；abs表示取絕對值。

④ 任務服務時長

用戶根據其需求對任務進行評估后提交的信息。在本文的實驗中，根據隨機數和正態分布來生成。任務服務時長為：

dt=abs(normrnd(mean,std))。

(15)

部分任務數據信息如表2所示。

表2 任務數據信息表Tab.2 Task data information

4.2 仿真實驗參數設定

在本文的實驗中，選擇86 400 s作為調度周期。然后根據不同的變量構建實驗，觀察不同變量的變化對整個動態調度優化效果的影響。最大參數規模可以達到500個任務申請、3顆中繼衛星、10個航天器。本次實驗的環境參數如表3所示。

表3 環境參數Tab.3 Environmental parameters

4.3 優化結果展示與算法性能分析

為研究NSGA-Ⅱ算法對中繼衛星動態調度的優化效果以及不同中繼衛星數量、用戶航天器數量和新增任務數量對優化效果的影響，本文選擇300個任務規模，做新增任務和用戶航天器數量變化實驗，在500個任務規模做中繼衛星數量變化實驗，并在相同條件下選取了經典的多目標算法SPEA-Ⅱ算法進行優化效果對比。

在本文中選用超體積指標(HV)做算法性能評價[16]，在雙目標優化問題中，HV的運算方法為獲得的非支配解集的每個個體與參照點(最大值個體)在空間中圍成的矩形的面積之和，HV值越大，說明算法的綜合性能越好。

(16)

4.3.1 300個任務申請

在300個任務規模時，將中繼衛星數量固定為2，考慮此基礎上的優化效果以及不同新增任務數量和不同用戶航天器數量對優化效果的影響。

① 新增任務數量對算法的影響

不同新增任務優化效果對比如圖5所示。

(a) 2個新增任務

(b) 4個新增任務

(c) 6個新增任務

(d) 8個新增任務

(e) 10個新增任務

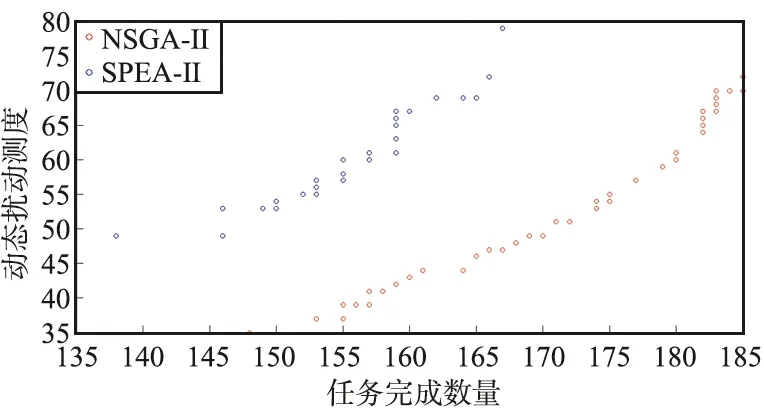
(f) 12個新增任務

(g) 14個新增任務

(h) 16個新增任務

(i) 18個新增任務

(j) 20個新增任務圖5 優化效果對比Fig.5 Optimization effect comparison

不同新增任務優化數據對比如表4所示。

表4 優化數據對比Tab.4 Optimized data comparison

圖6展現了在300個任務、2顆中繼衛星、10個用戶航天器的條件下，不同新增任務的優化效果，輸出的為在同樣迭代次數下SPEA-Ⅱ和NSGA-Ⅱ算法優化后種群的Pareto最優值。

圖6 HV值對比Fig.6 HV value comparison

由圖6可以看出，在新增任務數量不同時，NSGA-Ⅱ算法輸出的Pareto最優解在空間上分布的均勻性、收斂性和廣泛性相較SPEA-Ⅱ算法都更加優秀。

對比圖5可以看出，HV值相較SPEA-Ⅱ要更大，說明NSGA-Ⅱ算法在中繼衛星動態調度優化方面性能更好，能優化出收斂性和多樣性更佳的非支配個體。

② 對算法的影響

不同用戶航天器數量優化效果對比如圖7所示。

(a) 2個用戶航天器

(b) 4個用戶航天器

(c) 6個用戶航天器

(d) 8個用戶航天器

(e) 10個用戶航天器

(f) 12個用戶航天器

(g) 14個用戶航天器圖7 優化效果對比Fig.7 Optimization effect comparison

不同用戶航天器數量優化數據對比如表5所示。

表5 優化數據對比Tab.5 Optimized data comparison

圖8展示了在300個任務、2顆中繼衛星、10個新增任務的情況下，不同用戶航天器數量對優化效果的影響。

由圖8可以看出，在300個任務條件下，僅用2個用戶航天器承載任務會導致任務的完成率減少，這是由于任務的服務時間和航天器與衛星的可見時間匹配隨機概率減少。在不同的用戶航天器情況下，NSGA-Ⅱ算法展現了較強的優化性能，得到的Pareto最優解適應性、均勻性和收斂性都較好。

圖8 HV值對比Fig.8 HV value comparison

4.3.2 500個任務申請

500個任務時，將用戶航天器數量固定為10個，考慮此基礎上的優化效果及不同中繼衛星數量對優化效果的影響。500個任務規模也和300個形成對比，展現不同任務數量時，對優化結果的影響，優化效果對比如圖9所示，優化數據對比如表6所示。

(a) 2顆中繼衛星

(b) 3顆中繼衛星

(c) 4顆中繼衛星圖9 優化效果對比Fig.9 Optimization effect comparison

表6 優化數據對比Tab.6 Optimized data comparison

圖10展示了在500個任務、10個用戶航天器、10個新增任務的動態擾動環境下，變化中繼衛星數量，對算法優化效果的影響。

圖10 HV值對比Fig.10 HV value comparison

隨著資源數量的增加，任務完成率也隨之增加，且NSGA-Ⅱ算法的優化結果分布更均勻，種群多樣性更高，同時NSGA-Ⅱ算法的性能，即HV值，要優于SPEA-Ⅱ算法。

5 結束語

在中繼衛星單址天線調度問題基礎上，考慮調度需求多樣性，構建了多目標函數的中繼衛星重調度模型，在生成初始調度方案后，運用NSGA-Ⅱ算法對初始調度方案進行優化。仿真實驗中，本文對比了在實驗參數，如任務規模和資源數量等變化的情況下，NSGA-Ⅱ算法的優化情況。其總能優化得到一個收斂性、均勻性和廣泛性較好的Pareto最優解。在對比SPEA-Ⅱ這一經典多目標算法時，NSGA-Ⅱ展現了更強的適用性，基于多目標優化的NSGA-Ⅱ算法輸出的Pareto最優解，為調度方案提供了多樣化的選擇，為中繼衛星管理部門和用戶建立了一個較佳的選擇空間。