讀懂教材內容的實質與邏輯

劉曉婷

【摘? ?要】教材是教師進行教學的重要資源，備教材是教學的重要環節。但當前教學中仍存在忽視教材的現象。從一道“扣分”測試題帶來的困惑出發，通過調研了解到教師在分數乘分數（分數除以整數）圖式表征中的理解失之偏頗，回歸教材分析背后的原因，提出讀懂教材內容實質與邏輯的三個角度：審慎眼光思教材、進階視野觀教材、動態視角析教材。

【關鍵詞】教材內容理解;分數乘分數;分數除以整數

教材是教師進行教學的重要資源，是教學活動設計的藍本。教師在備課過程中，對教材進行細致的分析、梳理是非常重要的環節，是制訂教學目標、把握教學重難點、設計教學活動及選擇教學策略的重要依據之一。然而教師對教材作用的忽視，導致教學中存在一些問題。例如，在展示課或比賽課中，為了凸顯教學的創新性，教師對教材棄置不用，進行“隨意的創造”;在日常教學中，“機械”使用教材，忽視學生的困難等。在當前“雙減”核心任務下，反觀這些現象，亟待一線教師回歸對教材進行解讀，重視對數學教材的分析，深度理解教材中的教學內容，設計有效的教學活動，提升課堂教學質量。下面，從一道“扣分”測評題帶來的困惑談起，追尋其背后的根源，簡析讀教材的視角。

一、研究緣起：一道“扣分”測試題帶來的困惑

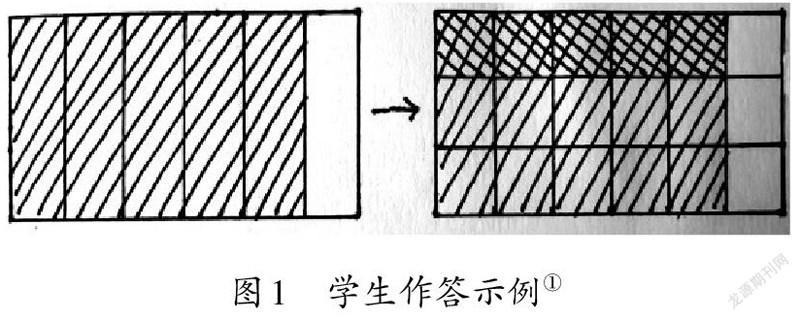
某區六年級期末測試中有一道題目，“畫圖表示‘5/6÷ 3’的過程和結果”。某生作答情況如圖1所示，在判卷時教師扣掉了學生的一半分。

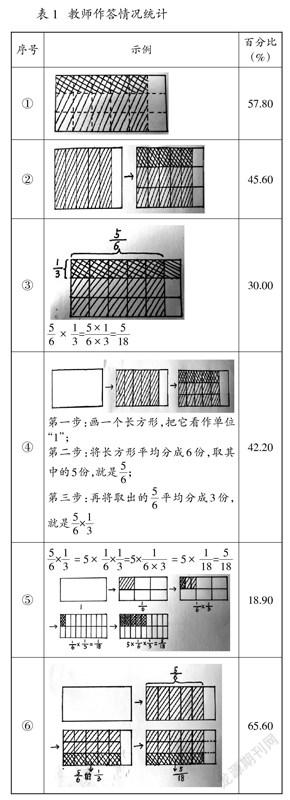
判卷教師給出的扣分理由是“學生沒有標注數據”，但學生認為“本題要求畫圖表示，并未對標數據做要求”。暫且不考慮題目表述嚴謹性的問題，“5/6÷3”究竟應該如何畫圖表示呢？學生畫的圖有問題嗎？如果有，問題是什么？筆者把題目稍作調整后，對19位教齡為5～10年的優秀青年教師進行調研，請他們“畫圖表示‘5/6×1/3’的過程和結果”，得到六種主要類別的圖式。之后以投票的形式，對90位在職小學數學教師進行調研，讓教師選出贊同的圖式，結果如表1所示。

由上表可見，六個圖式全部有人支持。其中圖式⑥的支持率最高，約為65.60%，圖式⑤的支持率最低，約為18.90%。圖式②和學生作答示例（如圖1）相同，支持率約為45.60%。這一調研結果說明了什么，能帶給我們怎樣的啟示呢？

二、追本溯源：調研數據引發的問題與思索

上述案例引發如下問題：第一，哪種圖式能更準確地表示“5/6×1/3”的過程和結果？如何用圖式準確、恰當地表示分數乘分數（分數除以整數）的計算過程？第二，為何教師在畫圖時會有如此多樣的表達？其根源是什么？筆者結合文獻研讀、教材梳理、教師訪談等方式，作如下闡釋。

（一）圖式分辨：緊扣運算意義，直觀精準地表達計算過程

對比表1中的六個圖式，有如下區別：其一，圖式①和③沒有體現出計算的過程，圖式②④⑤⑥給出了計算過程，部分圖式過程很完整。其二，圖式①內部線全部為虛線，其他幾個圖式內部大多為實線，其中圖式⑥最右側空白位置為虛線。其三，圖式④⑤⑥在第三步“分成三份”時，分割線均未延長，而圖式②的第二步分成三份時，分割線直通最右側，圖式①③類似。其四，圖式⑤平均分成6份的方式與其他圖式不同，采用了橫縱切割法，同時還把5/6轉為化“1/6×5”，步驟較多。其他圖式平均分成6份時，采用縱向切割法，平均分成3份時采用橫向切割法。

不同圖式之間的差別進一步聚焦到三個問題：（1）把一個長（正）方形平均分成6份，取其中的5份，老師們沒有異議。分歧在于接下來分的3份，分的對象是誰。（2）把一個長（正）方形進行分割時，用實線還是用虛線，還是虛實線結合？其中的道理是什么？（3）畫圖表示方式是否只有一種？

不論是“5/6×1/3”，還是“5/6÷3”，其意義均可解釋為“把5/6平均分成3份，求其中的1份”，即分成3份的對象應該是5/6，圖式④⑥都清晰地表示了這一意思。但分完3份并取出其中的1份后，這時的1份究竟是多少，還需要明晰其與單位“1”的關系，圖式⑥的最后一步，把分割線進行延長后，可以清晰地看到這部分是單位“1”的5/18。按此解釋，圖式⑥準確表示了算式和結果的意義。其中虛線的使用是為了更好地區別分割和確認結果兩個部分，能夠讓別人看清思考的過程。此外，圖式⑤做了轉化，雖然分割方法較復雜，但還是準確表征了所給出的算式的意義。

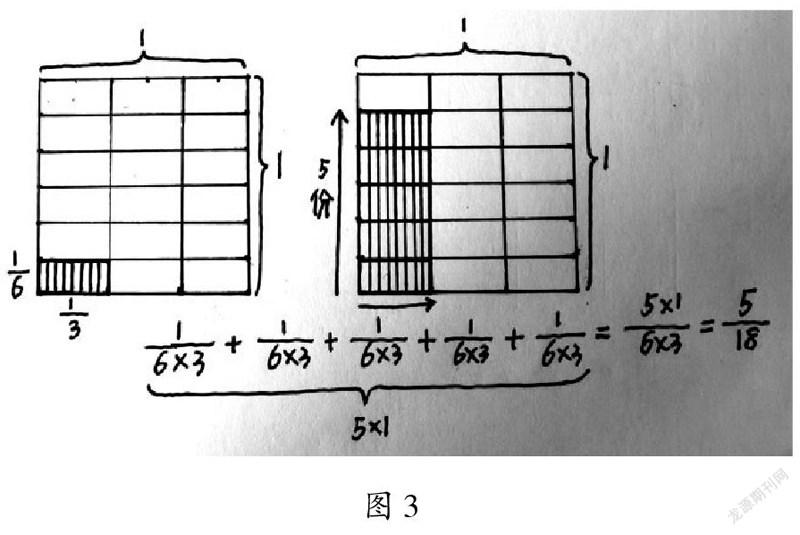
分數乘分數的意義還可有另外一種解釋，數學家伍洪熙把邊長等于m/n和k/l（這里的n，l都是非零自然數）的矩形稱為邊長為m/n和k/l的矩形，并由此定義分數乘法：m/n×k/l=邊長為m/n和k/l的矩形的面積。對于任意自然數l>0，n>0，有1/n×1/l=1/nl，如圖2（左）所示。對于任意分數m/n和k/l，一般乘積公式m/n×k/l=mk/nl成立。此時把m/n看成由m條長為1/n的線段拼接而成，k/l看成由k條長為1/l的線段拼接而成。如圖2（右）所示，大矩形恰好是由m/k個這樣全等的小矩形拼接而成，其面積等于1/nl+1/nl+…+1/nl=mk/nl[1]。

表1中的圖式③貌似和圖2有相似之處，但仔細分析還是有差別。圖2中使用的是矩形的面積來定義分數乘法，是把單位正方形進行分割，以5/6×1/3為例，1/6×1/3是基于定義得到的，定義及運算規則有嚴格的推導過程，計算過程用圖3表示。而表1圖式中老師們的想法是基于“某物的m/n”這一定義，即m/n×k/l=分數m/n的k/l。在表1所示的圖式中，都是用長方形代表單位“1”，先表示出5/6，再來表示5/6的1/3。

（二）根源初探：讀教材淺嘗輒止導致理解失之偏頗

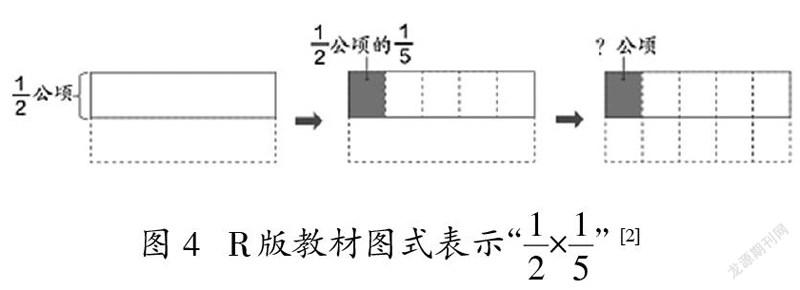
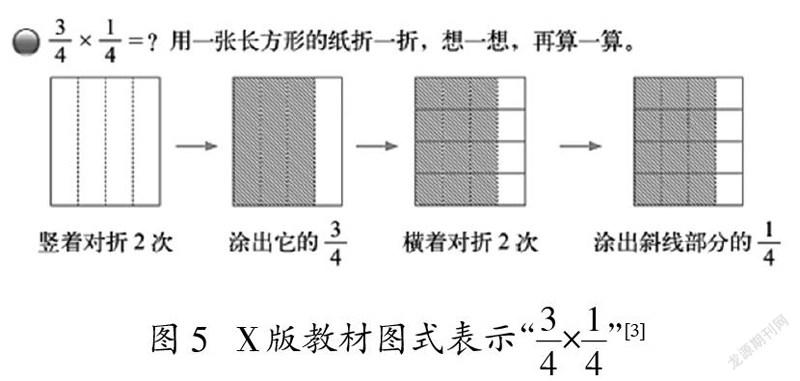
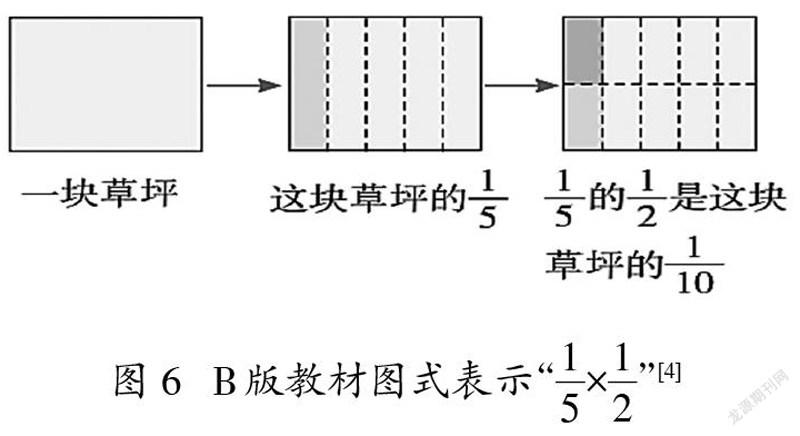
為何老師們在畫圖時會出現如此多的樣態呢？通過訪談了解到，這與教師對教材的認知有關。以R、X、C三個版本的教材為例，三個不同版本的教材在用圖解釋分數乘分數時存在差異，如圖4～6。

三個版本教材在用圖式表示分數乘分數時全部給出了計算過程圖。表示第一個因數時基本相似，只有R版教材用虛線表示了單位“1”的另一部分。差異最大部分仍是m/n的k/l的表示方法，R版教材先把1/2平均分成5份，得到1/2的1/5，之后再用虛線延長分割線，得到10個格子，1/2的1/5正好是10個格子中的1個，即為1/10。X版教材以“折”表示分割，得到3/4后再“橫著對折兩次”，但此時的“對折”直觀呈現的是平均分整個長方形（B版教材一條虛線橫穿長方形），從平均分的對象上來看，容易造成誤解。用圖式表征，其目的是幫助學生直觀理解學習內容，理解計算結果的合理性，教師需要明辨圖式的準確性、適宜性。

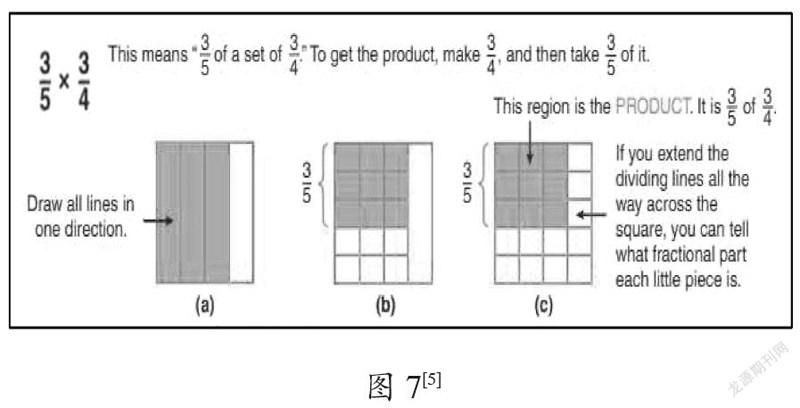
參閱其他教材和教學資料，關于分數乘分數的圖式表示方法，有些方式值得借鑒。如圖7（c），就標注了延長線的意義，即“把分割線延長至正方形，就能知道代表每一小塊兒的分數是多少”。

在討論“分數乘分數”的圖式時，有教師認為圖式⑥過于煩瑣，認為如圖式②所示，兩步足夠，并給出了“證據”——R版教材在圖式表示分數除以整數時就只畫了兩步（如圖8）。對該教師的質疑如何回應呢？筆者以為，教師應當關注教材內容呈現的進階。分數乘分數在分數除以整數之前，R版教材兩幅圖的差異也恰好表明了教材在設計呈現內容時考慮到了兒童數學學習的經驗，在分數乘分數圖形表征學習的基礎上，分數除以整數圖式可以做適當的刪減，而在關鍵部分，教材還是進行了巧妙且精準的表達，在把4/5平均分成兩份時，前面仍用實線表示分的對象是4/5，后面用虛線延長確認每個小格的分數值。但遺憾的是，教材編寫者的編寫意圖被部分教師忽視了。

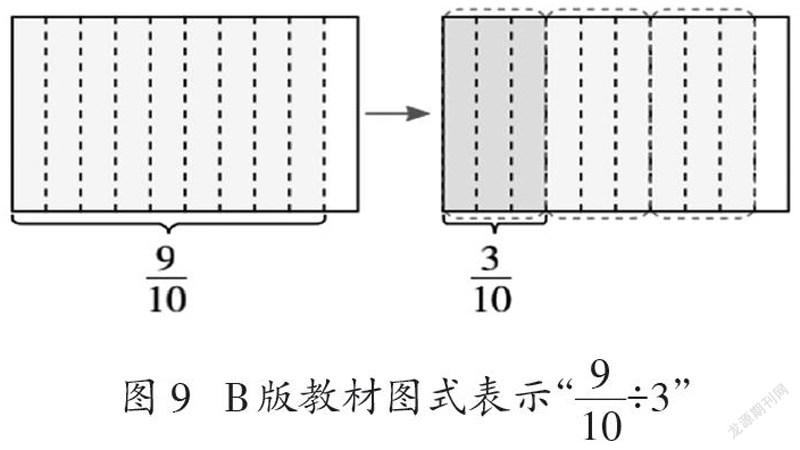
此外，在對19位教師的調研中，僅有一位教師畫出了圖式⑤，該種畫法在調研中的支持率僅為18.90%，這同樣與教材呈現有關。仍以上述三個版本教材為例，分數乘分數及分數除以整數的圖式，教材多采用的是先縱向分割，后橫向分割的方式，教師習慣于這些圖式后，形成了思維定式，對其他圖式的分辨能力有所下降。三個版本教材中只有B版教材的分數除以整數圖式表示給出了不一樣的形式（如圖9）。在第一步表示出9/10后，再思考9/10的1/3是多少，此時直接橫向分割可以得到結果，但由于數的特點，不分割也很容易把9/10分成三部分，每份是3個豎條，即為3/10。這樣的思考既體現了對學生數感和觀察能力的培養，也讓學生知道學習不要被模式所限制，靈活處理問題很重要。

反觀期末測試中那道被“扣分”的題目，學生回答時是否標注了數據并不是最要緊的問題，要緊的是那樣的圖式表征真的準確、恰當表明5/6÷3”的過程和結果了嗎？透過學生的回答，教師應反思之前是如何教學的，是否真的給學生理解分數運算提供了有效支持，用怎樣的題目能更好地考查學生對分數運算的理解，等等。

三、延伸思考：多維視角讀教材，明晰教學內容的實質與邏輯

基于上述案例及分析過程，對教材研讀和使用有如下思考。

（一）審慎的眼光思教材，明晰教學內容實質

教材是教學的藍本，教師在研讀教材時需要有審慎的眼光。棄置不用不可取，全盤接受不適當。案例中呈現的三個版本教材，有些對m/n的k/l的表示方法稍欠妥當。教師應結合學生的學情對教材內容進行審視，用問題驅動自我思考，“這里的表示學生能懂嗎”“學生都會這樣想嗎”，等等。教材是以文本的形式承載編者的思想和意圖的。教師在進行課堂教學設計時，要與教材進行“對話和交流”，從而把握教學內容的實質。教師應以審慎的眼光分析和思考教材，將靜態的教材內容轉化為動態的學習活動。

（二）進階的視野觀教材，厘清教學內容邏輯

教材在編排教學內容時是有邏輯的，教師應以進階的視野看教材，明晰相關內容之間的聯系。上述案例中，分數乘分數和分數除以整數在意義上具有一致性，R版教材在處理直觀圖式時就考慮到了內容的關聯性，在圖式呈現方式上有所變化，體現了內容及思維的進階。數學教材中的諸多內容存在著緊密的聯系，前面內容的教學應為后續內容的學習積累知識、方法、思維經驗，后續內容就應當在此基礎上進行教學。但在教學中，我們常看到教師回歸原點，忽視教材內容邏輯，忽視學生的知識、方法以及思維經驗。備教材時，關注這種“瞻前顧后”的承接性十分必要。

（三）動態的視角析教材，有效設計教學活動

教學不應是“教教材”，而應是“用教材教”。這就需要教師以動態的視角解析教材。仍以案例中的分數乘分數為例，三個版本教材以過程全景圖的形式呈現了計算的過程。教師備教材時可考慮以動態課件的形式呈現平均分的過程，選擇表征方法的過程，再平均分的過程，以及確認結果分數的過程。此外，結合學生實際對教材情境恰當地進行再加工，對教學任務進行適當的分解、整合、重組等都是動態視角下解析教材的路徑，也是有效設計教學活動的前提。

備教材是教師的基本功，教師要專精覃思讀教材，讀懂教材內容的本質與邏輯，為教學媒體和策略的選擇提供依據，為實現高質量教學積蓄力量。

參考文獻：

[1]WU H. Understanding numbers in elementary school mathematics[M]. Washington： American Mathematical Society， 2011： 263， 266， 267.

[2]盧江，楊剛.義務教育教科書數學六年級上冊[M].北京：人民教育出版社，2019.

[3]劉堅，孔企平，張丹.義務教育教科書數學五年級下冊[M].北京：北京師范大學出版社，2014.

[4]北京教育科學研究院.義務教育教科書數學六年級上冊[M].北京：北京出版社，2014.

[5]JOHN A， WALLE V D， KAREN S. Elementary and middle school mathematics teaching developmentally：Tenth edition[M]. New York： Pearson Education， 2019： 392.

（北京教育學院? ?100120）