(n，4，1，2)光正交碼的上界

牛心舒，黃月梅，2

（1.內蒙古師范大學 數學科學學院，內蒙古 呼和浩特 010022；2.內蒙古自治區應用數學中心，內蒙古 呼和浩特 010022）

1 引言及主要結果

令n，k，λa，λc是正整數，Zn是模n的剩余類加群，(Zkn)是Zn中所有k元子集的集合。一個(n，k，λa，λc)光正交碼（簡記為(n，k，λa，λc)‐OOC）是一些長度為n，漢明權為k的（0，1）‐序列的集合C，每個（0，1）‐序列稱為一個碼字并滿足下列條件：

（1）（自相關性）對任意A=(ai)∈C 和任意正整數r，r≡0(modn)有

（2）（互相關性）對任意A=(ai)，B=(bi)∈C 和任意整數r且A≠B有

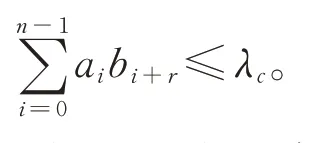
一個(n，k，λa，λc)‐OOC 的碼字數量稱為容量，通常用Φ(n，k，λa，λc)表示所有(n，k，λa，λc)‐OOC 的最大容量。當一個(n，k，λa，λc)‐OOC 的碼字數量達到了最大的容量則稱之為最優的。

光正交碼最早在文獻［1］中被研究。當λa=λc時光正交碼的上界以及構造問題已經被許多學者研究，可參考文獻［2-6］。當λa≠λc時，文獻［7］通過運用Skolem 序列及遞歸構造等方法研究了最優(n，3，2，1)光正交碼的容量問題；文獻［8-10］通過直接構造與遞歸構造等方法給出了最優(n，4，2，1)光正交碼的上界；當λ∈{1，2}時，文獻［11-12］解決了最優(n，4，λ，3)光正交碼的上界；文獻［13］給出了最優(n，4，3，2)光正交碼的容量與一些遞歸構造；文獻［14］研究了更為一般性的(n，k，k-2，k-1)光正交碼的上界問題；同時在文獻［15-16］中得到了最優(n，5，2，1)光正交碼的一些無窮類。本文主要通過3‐子集軌道出現在碼字中的次數，給出最優(n，4，1，2)光正交碼的上界。

定理1對于任意正整數n有

2 預備知識

設C 是一個(n，k，λa，λc)‐OOC，對于任意（0，1）‐序列A∈C，若在Zn上構造一個k元子集BA，有i∈BA，當且僅當A中第i個位置是非零的。集合{BA：A∈C}中的k元子集就與C 中的（0，1）‐序列形成一一對應關系，通常將這樣的k元子集的集合記為B。

例1下 列 四 個（0，1）‐ 序 列 構 成 一 個 (13，4，1，2)‐OOC，即 1101000001000，1100101000000，1100010000010，1100000000100，通過子集的概念，一個(13，4，1，2)‐OOC 中的碼字可通過Z13上的4‐元子集給出{0，1，3，9}，{0，1，4，6}，{0，1，5，11}，{0，1，8，10}。

對 于 任 意B∈B，定 義O(B)={B+i：i∈Zn} 為B在Zn作 用 下 生 成 的 軌 道，其 中B+i={b+i(modn)：b∈B}，這樣()中的所有k元子集可以被劃分為一些軌道的并集，每個O(B)中的k元子集稱之為區組。通常用|O(B)|表示軌道中不同區組的個數，若|O(B)|等于n則稱之為長軌道，否則為短軌道。

對于任意Zn中的k元子集B，定義集合ΔB={a-b(modn)：a，b∈B，a≠b}為B的差多重集，再定義ΔB的支撐集為集合中所有不同元素的集合，記作supp(ΔB)，令λ(B)記為ΔB中所有差重數的最大值，則有

根據文獻［13］可用差集與3‐子集軌道代表元出現在碼字中的次數給出一個(n，k，λa，2)‐OOC 的等價表述。令B 是Zn中k元子集的集合，若B 滿足以下兩個條件，則它構成一個(n，k，λa，2)‐OOC：

（1）（自相關性）λa=max{λ(B)：B∈B}；

（2）（互相關性）每個3‐子集軌道代表元最多出現在B 中的一個碼字中。

3 (n，4，1，2)‐OOC 的上界

建立Φ(n，4，1，2)較為緊密的上界，設B 是一個(n，4，1，2)‐OOC，對于任意B∈B，B為軌道O(B)的任意代表元，因此任一碼字B總可以表示為{0，a，b，c}的形式，其中a，b，c∈Zn{0}。

引理1［12］令B是Zn的任一包含0 元素的4‐子集。λ(B)=1，當且僅當|supp(ΔB)| =12。

引理2［13］令B是B 的任意4‐子集且λ(B)≤3。B包含三個不同的3‐子集軌道代表元，當且僅當B形如{0，a，2a，3a}，其中a∈Zn且a≠n5，2n5；B包含兩個不同的3‐子集軌道代表元，當且僅當B形如{0，a，2a，3a}，其中a∈{n5，2n5}；其余形式的碼字均包含四個不同的3‐子集軌道代表元。

引理3［9］令X={0，a，b}是Zn的任意3‐子集，則有

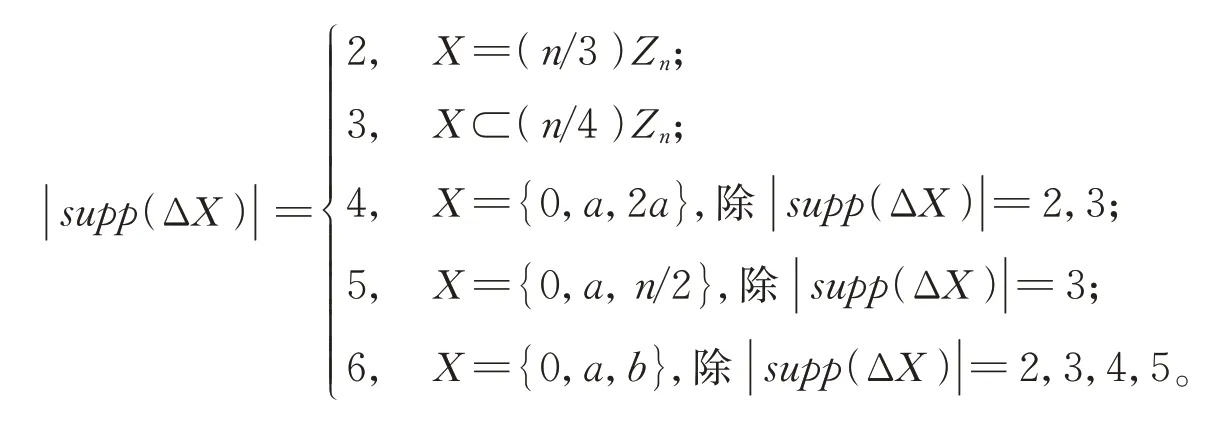
由引理3 可知，在Zn作用下只有O({0，n3，2n3}) 為短軌道，其余3‐子集均屬于長軌道。對于Zn中的任意3‐子集，當|supp(ΔX)| ≤5 時，這樣的3‐子集不能出現在B 的碼字中，否則與λa=1 矛盾。又因為Zn中的所有3‐子集可以被劃分為若干個不同的3‐子集軌道，故可記M(n)為|supp(ΔX)| =6 的3‐子集軌道的個數。

證明對于任意正整數n，設B 是一個(n，4，1，2)‐OOC。由引理2 可知B 中的每個碼字均包含四個不同的3‐子集軌道代表元，因此有

為確定Φ(n，4，1，2)的上界，需分情況討論M(n)的值。

對 于Zn中 任 一3‐子 集X，當(n，12)=12 時，() 中 包 含n3 個|supp(ΔX)| =2 的3‐子 集，n個|supp(ΔX)| =3 的3‐子集，n(n2-3)個|supp(ΔX)| =4 的3‐子集以及n(n2-2)個|supp(ΔX)| =5 的3‐子集，因此中包含|supp(ΔX)| =6 的3‐子集軌道的個數為

當(n，12)=6 時，中不存在|supp(ΔX)| =3 的3‐子集，包含n3 個|supp(ΔX)| =2 的3‐子集，n(n2-2) 個|supp(ΔX)| =4 的 3‐子 集 以 及n(n2-1) 個|supp(ΔX)| =5 的 3‐子 集，因 此中 包 含|supp(ΔX)| =6 的3‐子集軌道的個數為

當(n，12)=4 時，() 中 不 存 在|supp(ΔX)| =2 的3‐子 集，包 含n個|supp(ΔX)| =3 的3‐子 集，包 含|supp(ΔX)| =4，5 的3‐子集均為n(n2-2)個，因此(Z3n)中包含|supp(ΔX)| =6 的3‐子集軌道的個數為

當(n，12)=3 時，() 中 不 存 在|supp(ΔX)| =3，5 的3‐子 集，包 含n3 個|supp(ΔX)| =2 的3‐子 集，n((n-1) 2-1)個|supp(ΔX)| =4 的3‐子集，因此(3)中包含|supp(ΔX)| =6 的3‐子集軌道的個數為

當(n，12)=2 時，() 中 不 存 在|supp(ΔX)| =2，3 的3‐子 集，包 含|supp(ΔX)| =4，5 的3‐子 集 均 為n(n2-1)個，因此()中包含|supp(ΔX)| =6 的3‐子集軌道的個數為

當(n，12)=1 時中不存在|supp(ΔX)|=2，3，5 的3‐子集，包含n(n-1) 2 個|supp(ΔX)|=4 的3‐子集，因此()中包含|supp(ΔX)| =6 的3‐子集軌道的個數為

將以上所得M(n)的值分別代入（1）式，定理1 得證。

4 結語

本文主要通過計算碼字的3‐子集的方法確定了最優(n，4，1，2)‐OOC 的上界，所用到的計算方法具有一定的普適性，可推廣應用于二維(n×m，4，1，2)‐OOC 上界的構造，并有望獲得更多的結果。