基于多星聯合的雷達精度鑒定方法研究

陳 焱, 田堂勝， 祝開建,3， 王啟超， 王蔚東， 黃志詢

(1.中國人民解放軍63768部隊， 陜西西安 710600； 2.中國電子科技集團公司第三十八研究所， 安徽合肥 230088； 3.宇航動力學國家重點實驗室， 陜西西安 710043)

0 引言

各國太空作戰力量的不斷發展對空間事件響應能力提出越來越高的要求。雷達作為空間目標探測的骨干裝備，為空間事件研判和處置提供了豐富的底層數據支撐。雷達測量精度是雷達的主要戰技術指標之一，代表雷達測量目標的準確程度，直接影響目標定軌精度，進而影響空間事件響應的準確性和敏銳性。因此，雷達數據匯集處理中心亟需建立常態化精度鑒定機制，快速、準確地分析雷達測量誤差，及時發現數據問題，提高裝備可靠性。

雷達測軌數據精度分析工作基于雷達標校技術得以開展，雷達標校技術經過長期的發展優化，形成了包括標校塔標校、氣球標校、微光電視星體標校、球載BD/GPS標校、射電星角度標校民航機標校、衛星標校等標校方法。其中，衛星標校方法可有效解決因雷達口徑大及分布地域廣不宜建標校塔的問題，但在實際應用中主要存在兩大制約因素，一是衛星精密軌道的易獲取性，這直接影響精度鑒定工作的便捷性；二是短時間內衛星相對雷達的過境頻次，這決定了精度鑒定工作的時效性。針對上述兩個問題，文獻[2-4]分別從標校星精密軌道確定方法、北斗精密星歷在裝備精度鑒定中的應用、多弧段衛星精密星歷誤差補償效果等方面展開研究，為雷達精度鑒定提供了有力參考。

結合文獻研究及常態化標校需求，本文提出了一種基于多星聯合觀測的雷達測軌精度鑒定方法，該方法以可公開獲取精密星歷的衛星為標校星，安排待標校雷達依次跟蹤多顆不同軌道高度的衛星以獲取具有差異性的原始數據，較好地解決了星歷獲取和短時間數據量積累問題，同時提出了計算單圈次跟蹤誤差、多圈次總誤差的方法綜合反映雷達測軌水平。基于多星聯合標校，本文對雷達測軌精度分析過程進行了詳細研究，并結合雷達實測數據對該方法在雷達測軌精度鑒定及裝備狀態監測中的應用意義進行了探討。

1 衛星標定原理

衛星標定以運行于空間近地軌道的人造地球衛星為基準目標。其基本原理為：被鑒定裝備跟蹤測量空間特定的衛星目標，獲取測量數據；同時，獲取該衛星對應于測量弧段的精密軌道數據，將測量數據與衛星精密軌道數據進行對比分析，結合裝備戰技術指標對其精度作出評估。可從隨機誤差、系統誤差和總誤差等多角度反映雷達測量數據精度，定義及公式如下：

1) 系統誤差

系統誤差反映測量值與真值的符合程度，即裝備測量的準確度，用測量值與真值一次差的均值定量表示。

=-

(1)

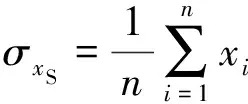
(2)

式中，表示雷達測量數據，表示對應時刻的衛星精密位置。

2) 隨機誤差

隨機誤差反映對同一真值進行的一組測量值的接近和符合程度，即裝備的精密度，用測量值與真值一次差的均方差值定量表示。

(3)

3) 總誤差

總誤差綜合反映裝備某一時間段內測量殘差的系統差及隨機差，用均方根誤差(RMSE)定量表示。

第圈次任務弧段總誤差為

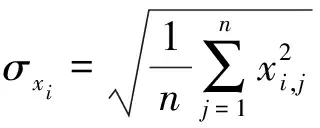
(4)

m個圈次任務的總誤差為

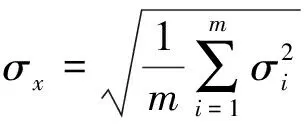
(5)

2 多星聯合標校可行性分析

雷達在跟蹤空間目標的過程中受大氣影響，導致對不同軌道高度的目標之間的測軌精度存在偏差，因此選取的標校星應盡可能覆蓋不同軌道高度以較全面的評估裝備跟蹤精度。同時考慮到精密星歷的易獲取性，優先選擇我國天平一號標校衛星及帶有激光反射器且參與國際聯測的衛星作為標校星，參考文獻[6]對開源CPF星歷精度的分析，選定LARETS、STARLETTE、LARES、AJISAI以及TianPing1A、TianPing1B等6顆衛星作為標校星目標集，衛星軌道信息如表1所示。

選擇4臺(套)布置于東線和西線的雷達裝備，對表1中的標校星作7日可見性分析，各裝備對每顆衛星日均可見圈次如圖1所示。由圖1分析可得，位于4個點位的雷達裝備對6顆標校星每天均有可見圈次，其中，位于東北線的雷達對LARES、LARETS、TianPing1A、TianPing1B等4顆衛星的日均觀測圈次較多，可達4～8圈次，東南線的雷達對LARES、AJISAI、STARLETTE等3顆衛星的日均觀測圈次可達3圈次以上，西南線的雷達對LARES、AJISAI、STARLETTE等3顆衛星的日均觀測圈次可達2圈次以上，西北線的雷達對LARES、AJISAI、STARLETTE等3顆衛星的日均觀測圈次可達3圈次以上。通過安排待鑒定雷達依次跟蹤3～4顆標校星，在綜合反映雷達對不同軌道高度目標之間測軌精度差異的同時，又可滿足較為緊急的裝備精度鑒定任務，基本可在一天內完成10圈次以上的數據積累。

表1 低軌標校星軌道信息表

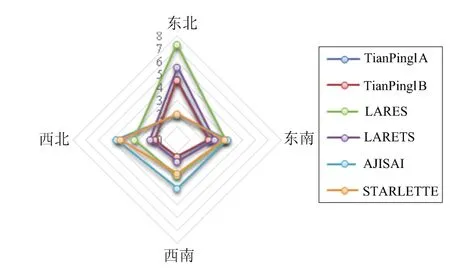
圖1 標校星日均過境圈次

3 精度分析計算方法

利用衛星精密星歷對雷達測軌數據進行精度分析，需先將衛星精密位置與雷達對目標的測量位置統一至相同的時間、空間基準下，然后將真值數據與修正后的觀測數據作差并進行數學統計。

3.1 標校星位置計算

3.1.1 時間轉換

CPF星歷以簡化的儒略日(MJD)和一天中的世界協調時(UTC)秒數給出衛星對應的時刻，而雷達測量數據的時間統一為北京時間(BJT)，其中MJD與公歷之間的轉換關系為

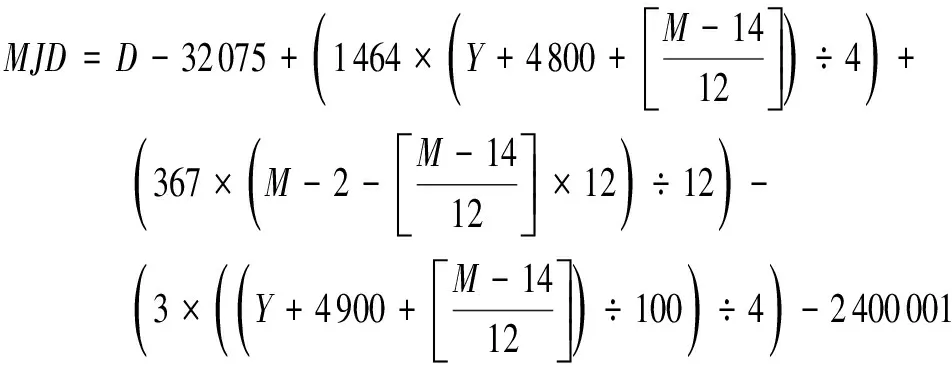
(6)

式中，，，分別表示公歷的年、月、日。

3.1.2 星歷插值

天平一號衛星軌道產品的時間間隔為10 s，CPF星歷時間間隔為180 s或240 s不等，而雷達測量數據的數據率較高，通常為0.05 s或0.5 s一個采樣點，即雷達觀測數據與精密星歷的時間不同步，需要通過插值或外推擬合來獲取雷達觀測時刻標校衛星的精密位置。格朗日多項式插值法被廣泛用于衛星軌道插值，其定義為:設在+1個時間為,,…，+1插值節點上衛星的坐標分別是(),(),…，(+1)，那么在任意時刻衛星的坐標可以表示為

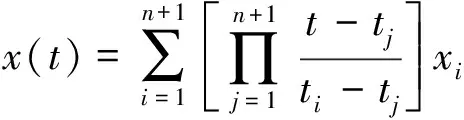
(7)

利用式(7)對精密星歷的、和方向分別插值處理，即可得到任意時刻衛星的位置。拉格朗日插值采用已知的多項式來近似，其階數與所選的插值節點的數量有關，若選取了個節點，則插值的最高次數為-1。需要注意的是，在一定范圍內插值階數越高，插值引入的誤差就越小，但并不是越高越好，一方面隨著插值階數的增加，計算耗時就越高，且需要更冗余的精密星歷，另一方面是因為在拉格朗日高次插值時易產生所謂的龍格震蕩現象，反而影響插值精度。文獻[7]研究表明，在插值點位于節點中央的情況下，插值階數不宜少于8階，當插值點不在節點中央時，插值的階數至少應達到9階。

3.1.3 坐標轉換

天平一號衛星星歷及CPF星歷均以地固坐標系為基準，需轉換至以待鑒定雷達為中心點的測站坐標系。由地固系轉為測站系可分兩步完成，首先利用坐標旋轉，將地固系坐標_轉換為以測站為中心點的東北天直角坐標_，然后將測站系下直角坐標_轉換為測站系下球坐標_。

定義繞、、軸的旋轉矩陣如下：

(8)

1) 地固系到測站東北天直角坐標系

轉換公式為

)(-)

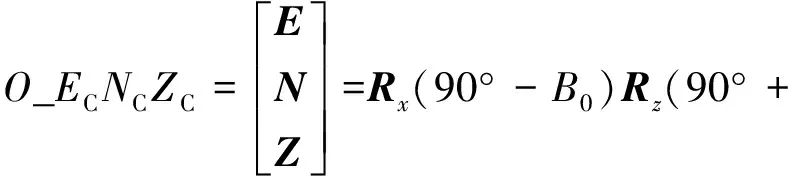
(9)

式中，為衛星精密位置，、、為雷達站大地經度、緯度和高度，為雷達站址在地心坐標系下的表示，與雷達站經度、緯度和高度可通過式(10)轉換得到

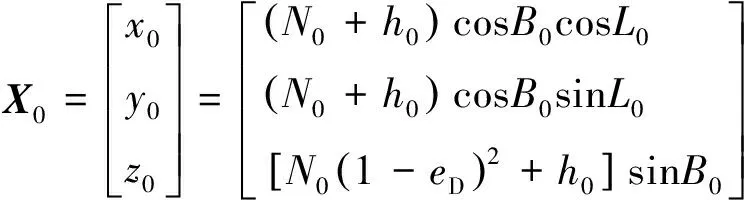
(10)

式中：

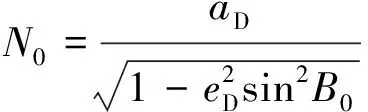
(11)

為地固系下的橢球長半軸,=6 378 137 m；為地固系下的橢球體的第一偏心率，=0.081 819 190 842 55。

2) 測站東北天直角坐標到測站極坐標

本質是將直角坐標系的三維參數轉化為球坐標系下的三維參數，結合測站坐標系下方位、俯仰的定義，轉換公式為

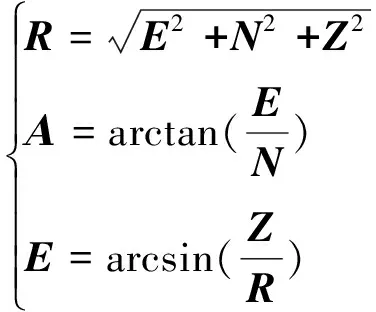
(12)

3.2 測量數據預處理

3.2.1 異常值檢測及修正

雷達測軌數據中因太空環境干擾、人員操作過失、數據傳輸線路故障等多種因素，往往存在明顯不合理的數據點，即野值點，這些數據點會對裝備精度分析結果造成干擾，應予以剔除或修正。利用經驗值法和最小二乘法可對野值進行識別檢測。

經驗值法是以空間目標相對雷達測量站的位置及目標運動屬性為依據，可推斷雷達測距、測速、測角符合以下規律：

距離>100 km，速度絕對值<9 km/s，方位角0°≤<360°，俯仰角0°≤<90°。對于不在范圍之內的數據即可確定為野值點，并進行剔除。

3.2.2 光行差修正

3.2.3 大氣折射修正

在語義網的七層結構中，根標記語言（XML Schema）層、資源描述框架（RDF Schema）層、本體（Ontology）層主要用于標識Web信息的語義，是系統的核心和關鍵所在［3］。通過對萬維網上的文檔添加能夠被計算機所理解的語義“元數據”，語義網使整個互聯網成為一個通用的信息交換媒介。在語義網的整體設計中，URI、RDF框架模型和本體的引入，打破了信息資源知識組織傳統的、平面的、單維的鏈接模式，形成了立體的、異構的、多維的語義鏈接。

對流層折射修正是對電磁波通過對流層時由于傳播速度的變化以及傳播路線彎曲而產生的折射誤差所進行的修正。

對于雷達測量數據，經典的大氣折射誤差修正公式如下：

通過式(13)～(14)計算得到大氣折射修正后測站至衛星空間距離值′：

′=-Δ

(13)

修正量Δ為

(14)

通過式(15)～(16)計算得到進行大氣折射修正后的俯仰角度值′：

′=-Δ

(15)

修正量Δ為

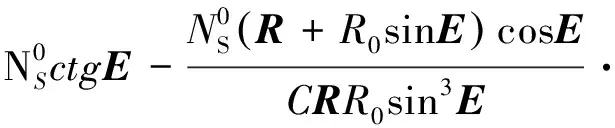
(1-e-20000)

(16)

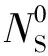
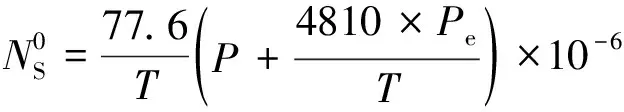
(17)

式中，地面水氣壓為

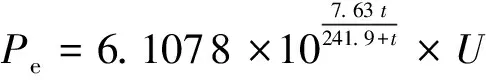
(18)

公式中涉及的參數意義見表2。

表2 大氣折射修正參量

4 應用案例

4.1 測軌精度鑒定

用本文方法對某型雷達測軌精度進行鑒定，該雷達精度指標為距離項優于10，方位項和俯仰項均優于360″，根據標校星選擇方法，選取1、1、和等4顆開源精密星歷精度在3以內且軌道高度不同的衛星作為本次精度鑒定試驗的標校星。

2021年2月15日至2月17日，安排該雷達跟蹤4顆標校星，對12圈次測量數據進行殘差統計計算，圖2～圖5為其中4圈次的殘差曲線圖，表3為12圈次殘差統計結果。在數據統計處理過程中，利用3門限對殘差較大的點進行了剔除，為達到較好的野值剔除效果，采用循環多次剔野值的方法，同時為保證合理的數據利用率，設置85為野值剔除下限并認定數據可用率不足85的測量弧段為質量較差弧段，不采信該弧段鑒定結果。

雷達于2月15日18時54分跟蹤衛星，共跟蹤534，測量354個點，對距離項、方位項、俯仰項分別進行野值剔除及殘差統計，其中距離項數據利用率為97，統計殘差均方差為5.47，殘差均值為-3.23；方位項數據率利用率為98，統計殘差均方差為202.69″，殘差均值為-31.50″；俯仰項數據率利用率為96，統計殘差均方差為188.21″，殘差均值為79.65″。距離、方位、俯仰3個測量維度的測量值與真值一次差隨時間變化曲線如圖2所示，距離項殘差以-3為基準上下波動，波動幅度基本保持在6以內，方位項殘差以-31″為基準上下波動，波動幅度基本保持在200″以內，俯仰項殘差以80″為基準上下波動，波動幅度基本保持在190″以內，殘差數值分布區域與殘差均方差值一致。

雷達于2月15日22時10分跟蹤衛星，共跟蹤748，測量493個點，對距離項、方位項、俯仰項分別進行野值剔除及殘差統計，其中距離項數據利用率為97，統計殘差均方差為8.91，殘差均值為-4.46；方位項數據率利用率為99，統計殘差均方差為166.22″，殘差均值為-44.66″；俯仰項數據率利用率為92，統計殘差均方差為77.71″，殘差均值為19.90″。距離、方位、俯仰3個測量維度的測量值與真值一次差隨時間變化曲線如圖3所示，距離項和俯仰項數據穩定性較好，方位項數據波動幅度較大。

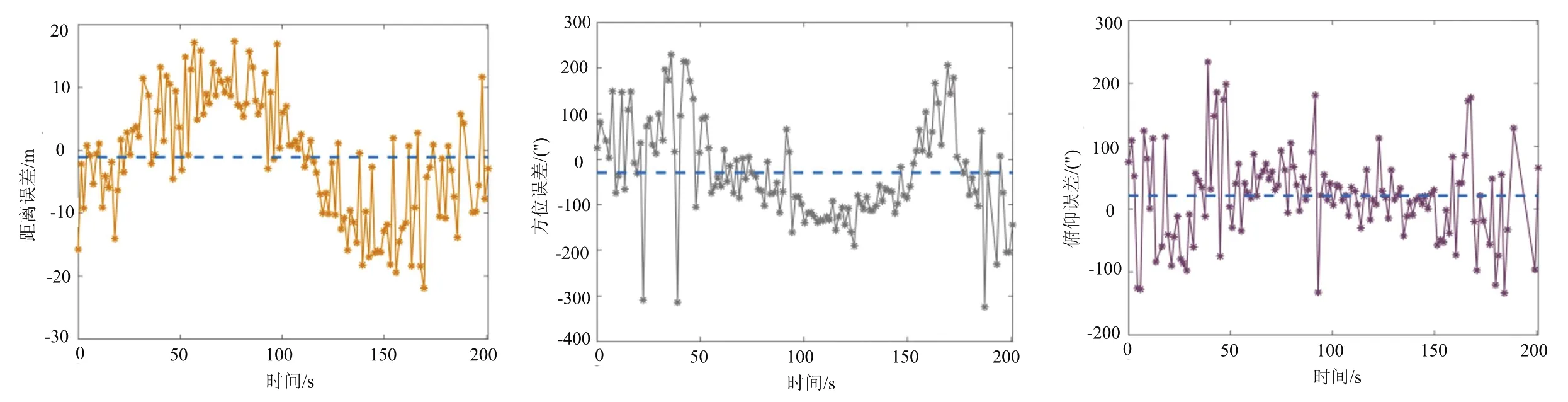
雷達于2月17日19時28分跟蹤1衛星，共跟蹤201，測量132個點，對距離項、方位項、俯仰項分別進行野值剔除及殘差統計，其中距離項數據利用率為99，統計殘差均方差為9.51，殘差均值為-1.09；方位項數據率利用率為98，統計殘差均方差為109.37″，殘差均值為-29.54″；俯仰項數據率利用率為95，統計殘差均方差為71.61″，殘差均值為21.19″。距離、方位、俯仰3個測量維度的測量值與真值一次差隨時間變化曲線如圖4所示，俯仰項數據穩定性較好，距離項和方位項數據波動幅度較大。

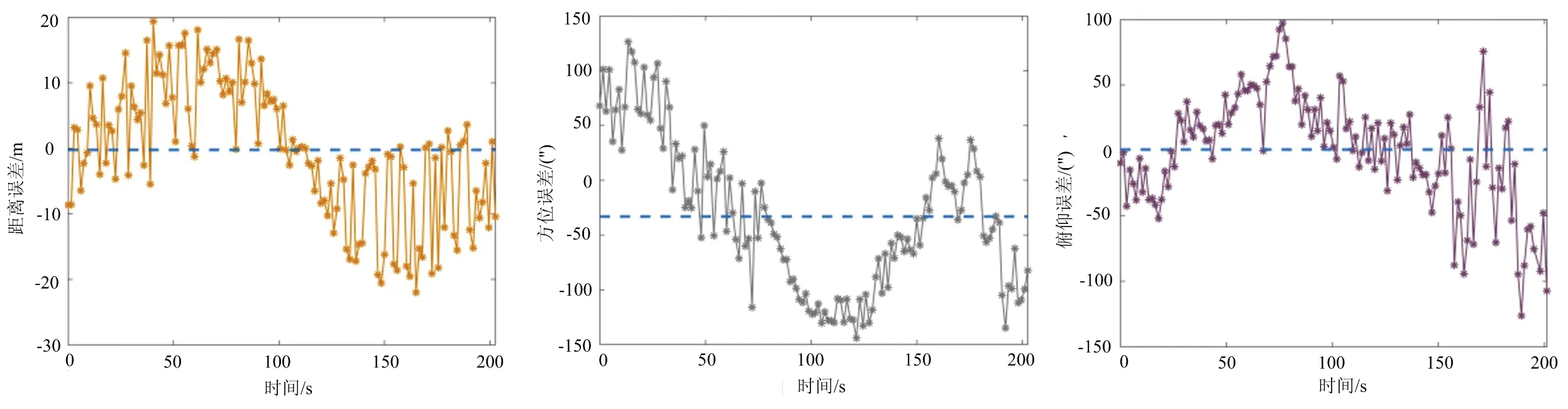
雷達于2月17日19時29分跟蹤1衛星，共跟蹤203，測量135個點，對距離項、方位項、俯仰項分別進行野值剔除及殘差統計，其中距離項數據利用率為100，統計殘差均方差為10.25，殘差均值為-0.24；方位項數據率利用率為100，統計殘差均方差為68.47″，殘差均值為-33.26″；俯仰項數據率利用率為99，統計殘差均方差為42.57″，殘差均值為0.65″。距離、方位、俯仰3個測量維度的測量值與真值一次差隨時間變化曲線如圖5所示，方位項和俯仰項數據穩定性較好，距離項數據波動幅度較大。

由表3可見，在計算過程中對野值點剔除后數據利用率保持在92以上，數據可用率較高。從12圈次數據殘差統計結果來看，距離項總誤差為8.94，方位項總誤差為142.28″，俯仰項誤差為163.04″，均優于裝備精度指標。從每圈次殘差統計結果來看，距離、方位、俯仰3個測量維度的系統差絕對值相對同維度的隨機差普遍偏小，說明該裝備3個測量維度的準確度高，但測量穩定性稍差；距離項系統差絕對數值小于5，但符號均為負值，后續通過修正距離系統零值可進一步提高測距精度水平。

(a) 距離項殘差圖 (b) 方位項殘差圖 (c) 俯仰項殘差圖圖2 跟蹤LARES衛星誤差殘差圖

(a) 距離項殘差圖 (b) 方位項殘差圖 (c) 俯仰項殘差圖圖3 跟蹤AJISAI衛星誤差殘差圖

(a) 距離項殘差圖 (b) 方位項殘差圖 (c) 俯仰項殘差圖圖4 跟蹤TianPing1B衛星誤差殘差圖

(a) 距離項殘差圖 (b) 方位項殘差圖 (c) 俯仰項殘差圖圖5 跟蹤TianPing1A衛星誤差殘差圖

表3 雷達A測量數據誤差統計表

4.2 裝備狀態監測

常態化開展精度分析計算可加強對裝備狀態的監測，當某裝備的測量精度長期處于不達標狀態時，可初步判斷該裝備狀態異常，應及時安排裝備端開展故障排查。

2020年5月2日在對某雷達歷史測量數據回查分析時，發現自2020年3月11日起測量數據的距離項誤差發生跳變，測距誤差遠超戰技指標。根據雷達端操作記錄發現，3月11日零點切換雷達跟蹤脈沖寬度，但未及時對該技術狀態進行精細標校，導致測距精度下降，定位問題后及時修正零值。圖6統計了該裝備2月28日至5月12日共計402圈次的測距系統差和隨機差，從誤差統計曲線可見，裝備測量狀態于5月3日恢復正常。這為雷達數據匯集處理中心及時預防數據庫污染提供有力監管。

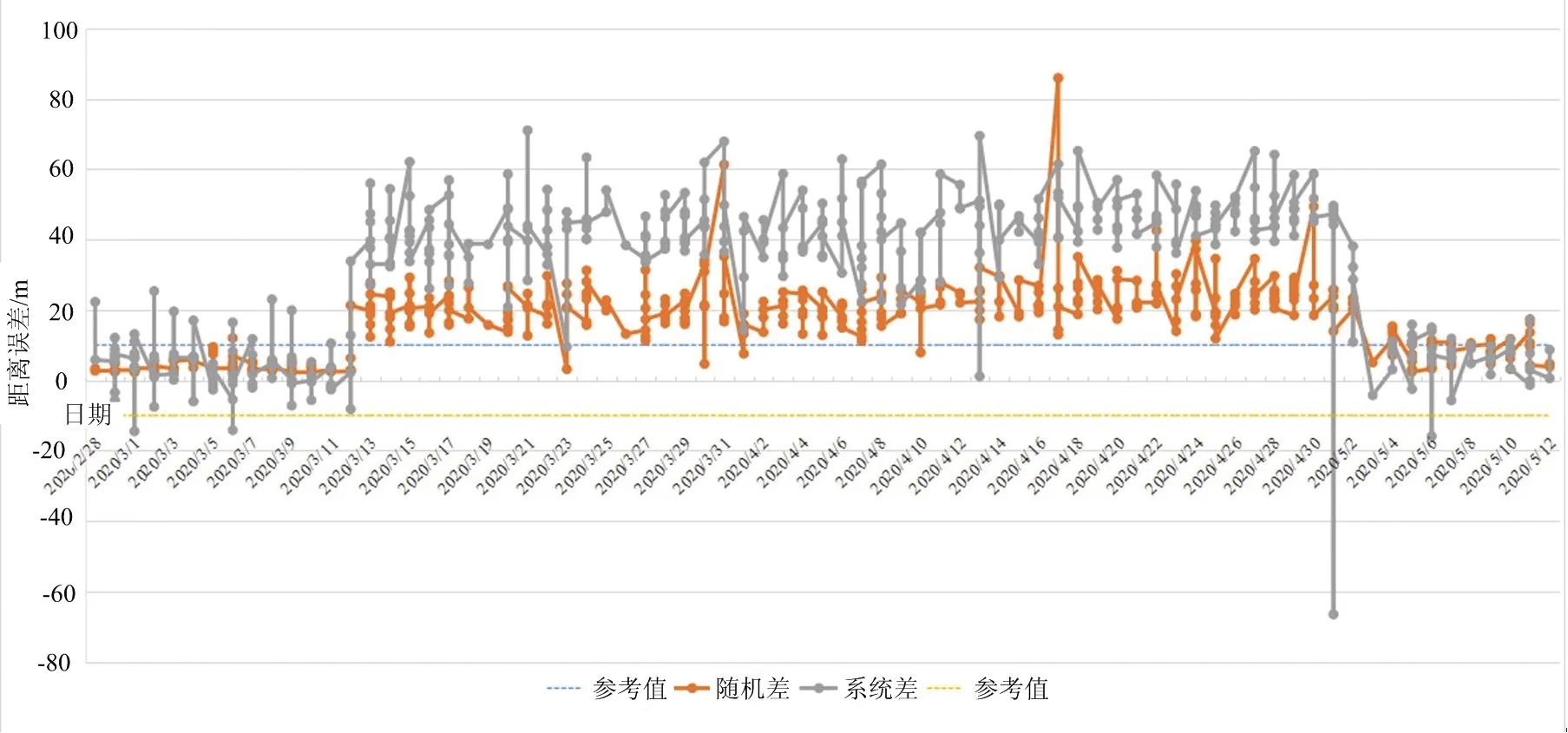
圖6 某雷達2020年2月至5月測距系統差和隨機差統計圖

5 結束語

本文研究了以多顆低軌衛星開源精密星歷為基準進行雷達測量數據精度鑒定評估的可行性及具體實施方法，分析了儒略日與公歷時之間的轉換關系、地固系坐標系與測站坐標系之間的空間轉換方法以及拉格朗日插值算法，完成了標校星相對測站的精確位置解算，研究了野值剔除、光行差修正、大氣折射修正等測量數據預處理算法。采用此方法，安排某型雷達聯合觀測TianPing1A、TianPing1B、LARES、AJISAI等4顆標校星，通過統計單圈次跟蹤殘差及3天內所有圈次跟蹤總誤差，鑒定了該雷達測距精度優于10 m，測角精度優于360″，根據統計規律，提出了進一步提高該雷達裝備測量精度的處理方向。結合應用實例，驗證了該方法在裝備精度鑒定及裝備狀態常態化監測中的有效性及科學性。