“數學物理方法”課程教學內容的組織探討*

趙曉云 李世剛 趙明

(阜陽師范大學物理與電子工程學院 安徽 阜陽 236037)

數學物理方法是高校物理類專業開設的一門專業必修課，它的先修課程是高等數學和大學物理，后續課程是理論物理相關課程[1～3]．數學物理方法課程內容主要包括復變函數和數理方程兩部分，它把數學理論、解題方法和物理實際三者緊密地結合在一起，在培養學生的數學運算能力、理論分析能力和創新思維能力方面有著重要的作用．這門課程的特點是內容多、公式多、推導繁瑣、與實際結合不緊密，加上現在高校課程課時的壓縮，教師課堂教學講解不能足夠細致充分，學生在學習時感覺特別難學，學習積極性普遍不高．

2019年，教育部明確提出提高高等教育人才培養質量的總要求，鼓勵高校嘗試采取各種有效措施，努力提高教學質量[4]．數學物理方法這門課程承上啟下，對于該門課程內容的掌握直接關系到后續其他課程的學習[5，6]．如何學好該門課程，是學生的一項重要任務，如何教好這門課程，則是教師的職責．數學物理方法這門課程難度系數較大，如何幫助學生提高知識接受程度和學習效率，是教師的重要工作．在“以學生為中心”的教育技術時代，教學模式也必須與時俱進，數學物理方法課程的教學改革也在不斷進行著．關于數學物理方法的教學方法與手段、教學內容等，很多學者已經提出了建議和改革措施，這些在一定程度上可以提高教學質量和學生的學習效率[7～16]．但是在已有的文獻中，關于課程內容的教學組織卻很少被提起，學生在學習的過程中對于知識點的把握仍然缺乏系統性，對知識結構的全貌缺乏整體認知，難以把握核心知識點，導致學習課程時出現只見樹木不見森林的問題．

筆者結合自身的教學實踐，就數學物理方法課程中所對應的復變函數論和數理方程兩大知識板塊，如何結合學生已有的基礎知識，對知識點進行梳理，建立課程知識圖，將課程內容構成更直觀的體系，便于學生更好地學習，以此提高教學質量和學生的學習效率，同時給同行在教學中作為參考．

1 復變函數論部分

復變函數論是數學的一個重要分支學科，其中內容主要包括復變函數的基本運算、積分、冪級數展開、留數定理以及傅立葉變換和拉普拉斯變換．復變函數解決一些問題主要依靠的是積分，復變函數微積分可以代表明確的物理意義，在理論研究方面和具體實際問題的解決中都具有重要意義，所以搞清楚復變函數的積分對掌握復變函數論知識至關重要．

1.1 復變函數的積分

復變函數的積分運算不同于實變函數積分運算，它不僅可能與積分的起點和終點有關，還可能與積分的路徑有關．盡管教材中關于復變函數的積分有柯西定理，但是涉及到具體積分時，學生仍然不知道怎么去運用，針對這種情況制作了復變函數積分運算方法知識結構圖，具體如圖1所示．

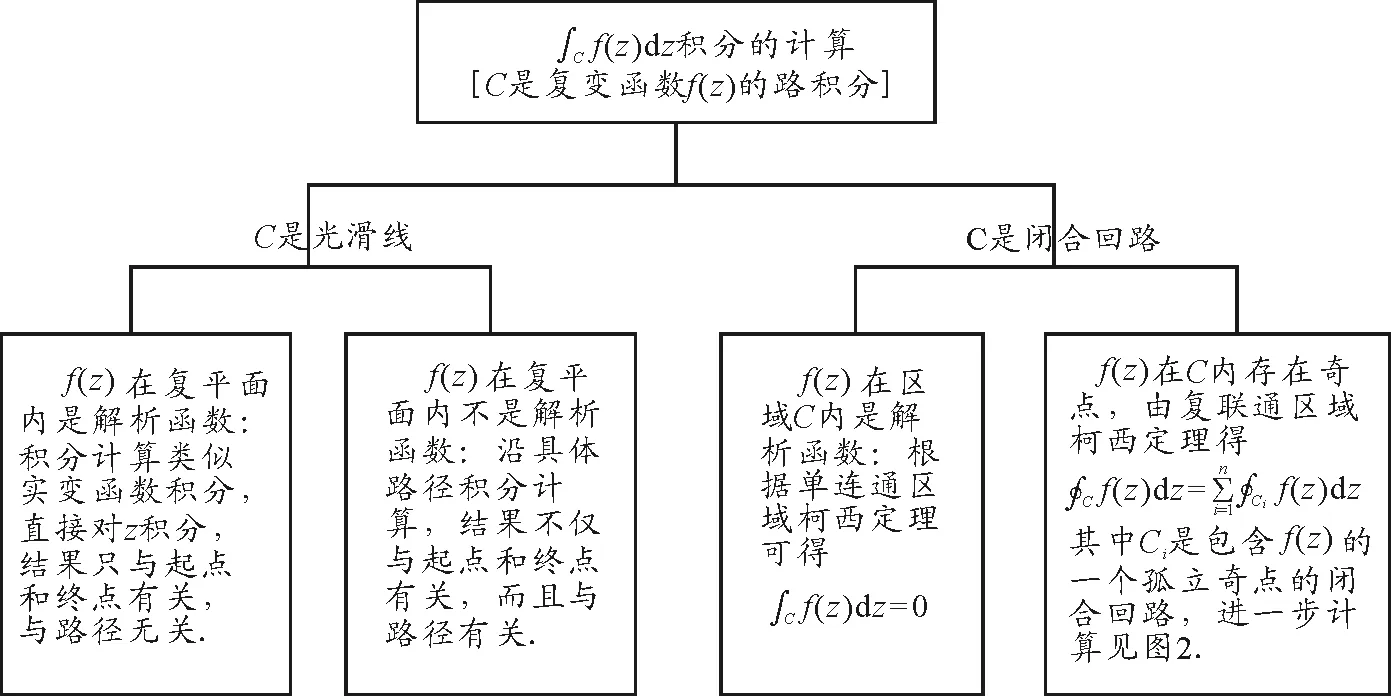
圖1 復變函數積分運算知識結構圖

對于復變函數沿著光滑曲線積分的計算問題，主要包括4種類型，分別是被積復變函數在積分區域內是解析函數和積分光滑曲線是有向線段；被積復變函數在積分區域內是解析函數和積分光滑曲線是閉合回路；被積復變函數在積分區域內不是解析函數和積分光滑曲線是有向線段；被積復變函數在積分區域內存在奇點和積分光滑曲線是閉合回路．從圖1可以看出，關于復變函數沿著光滑曲線積分的問題，主要難點是被積復變函數在積分區域內存在奇點和積分光滑曲線是閉合回路的積分計算，從圖1可以看出，對于這個類型問題的計算，首先要搞清楚被積函數在積分區域內孤立奇點的判斷．

1.2 孤立奇點的判斷

復變函數f(z)在z0不可導，但在z0的任意小鄰域內除z0外其他點處處可導，則稱z0為復變函數f(z)的孤立奇點．根據復變函數f(z)在z0的特點，又可將孤立奇點分為3種類型：可去奇點、極點和本性奇點．如何判據具體如圖2所示．

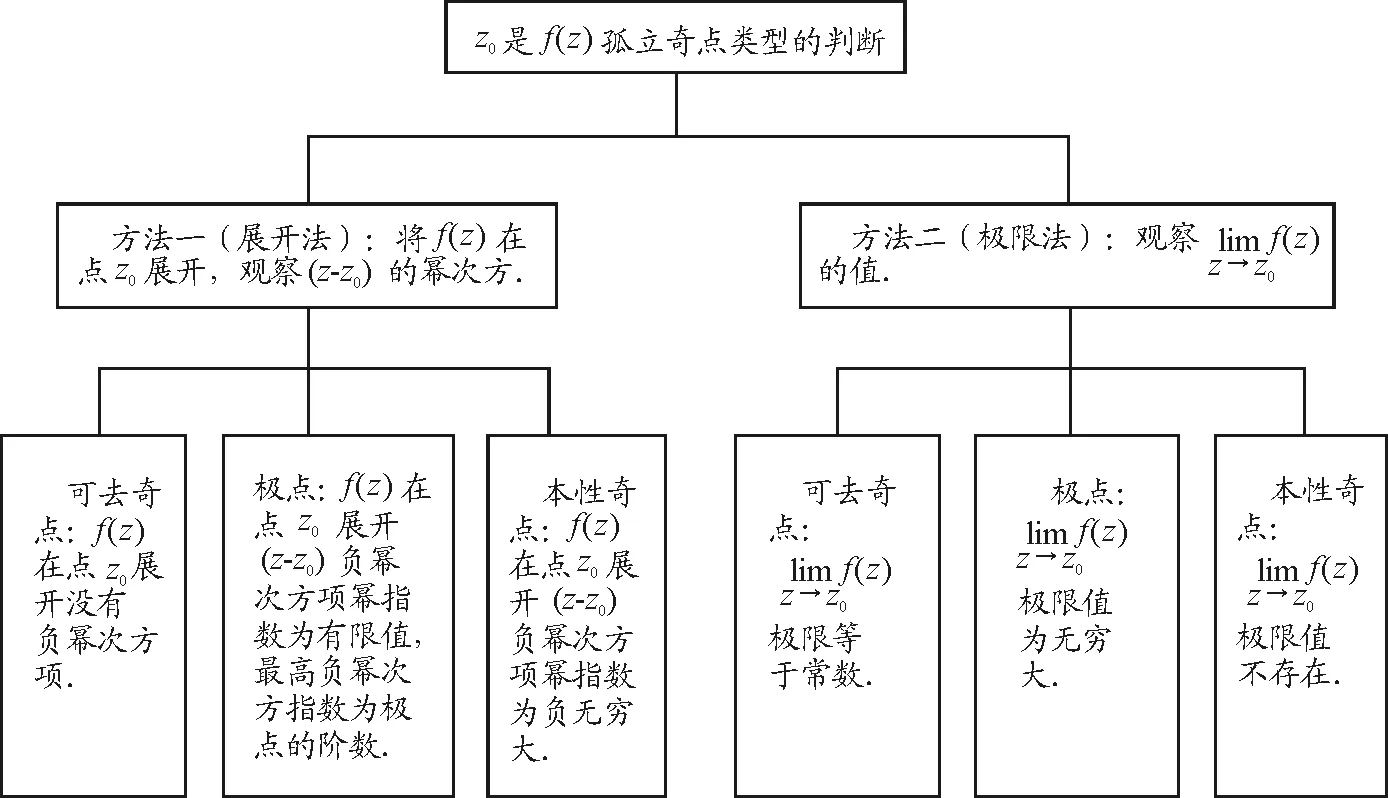
圖2 孤立奇點的判斷方法知識結構圖

關于指定點是復變函數孤立奇點何種類型的問題，從圖2可以看出，其中難點之一是復變函數在指定點展開的問題．復變函數f(z)在指定點的冪級數展開，主要有泰勒級數和洛朗級數，展開方式具體如圖3所示．

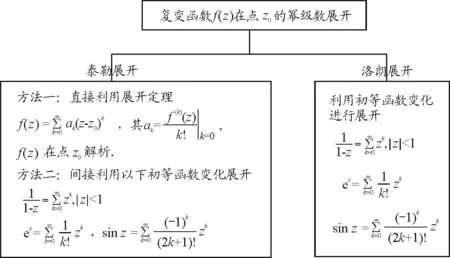
圖3 復變函數的冪級數展開知識結構圖

1.3 復變函數f(z)在閉合回路C內存在孤立奇點的積分

復變函數在指定點展開搞清楚之后，這樣計算圖1中復變函數沿閉合回路存在奇點的積分就容易計算了，具體如圖4所示．

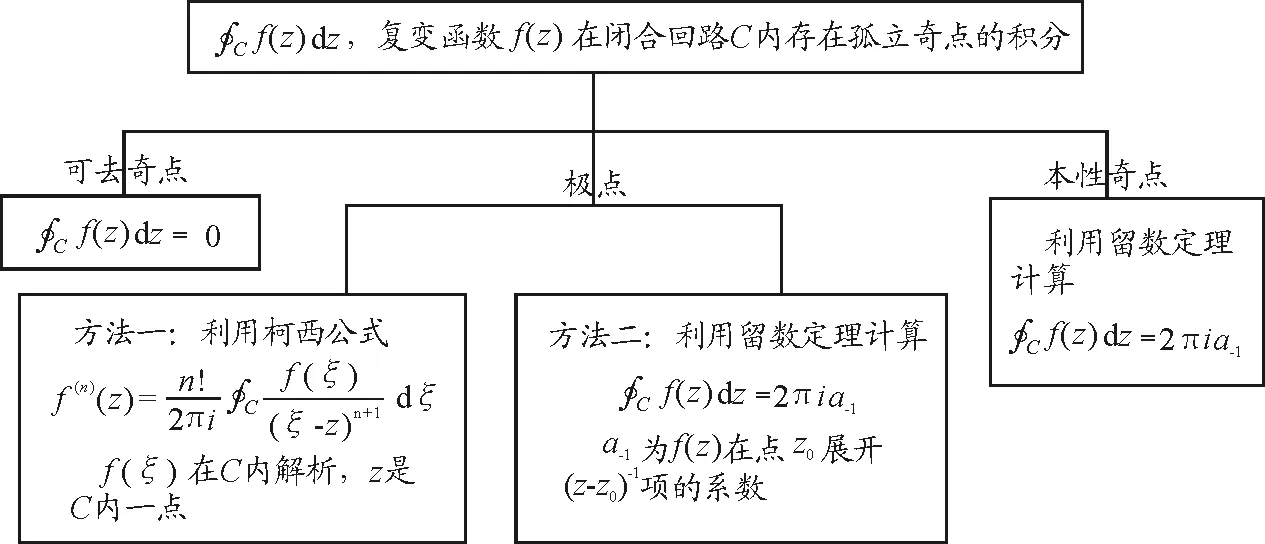
圖4 復變函數沿含有孤立奇點的閉合回路的積分知識結構圖

從圖4的結果可以看出，要想進一步計算出積分結果，必須要搞清楚復變函數f(z)在孤立奇點z0的留數a-1的計算，具體如圖5所示．

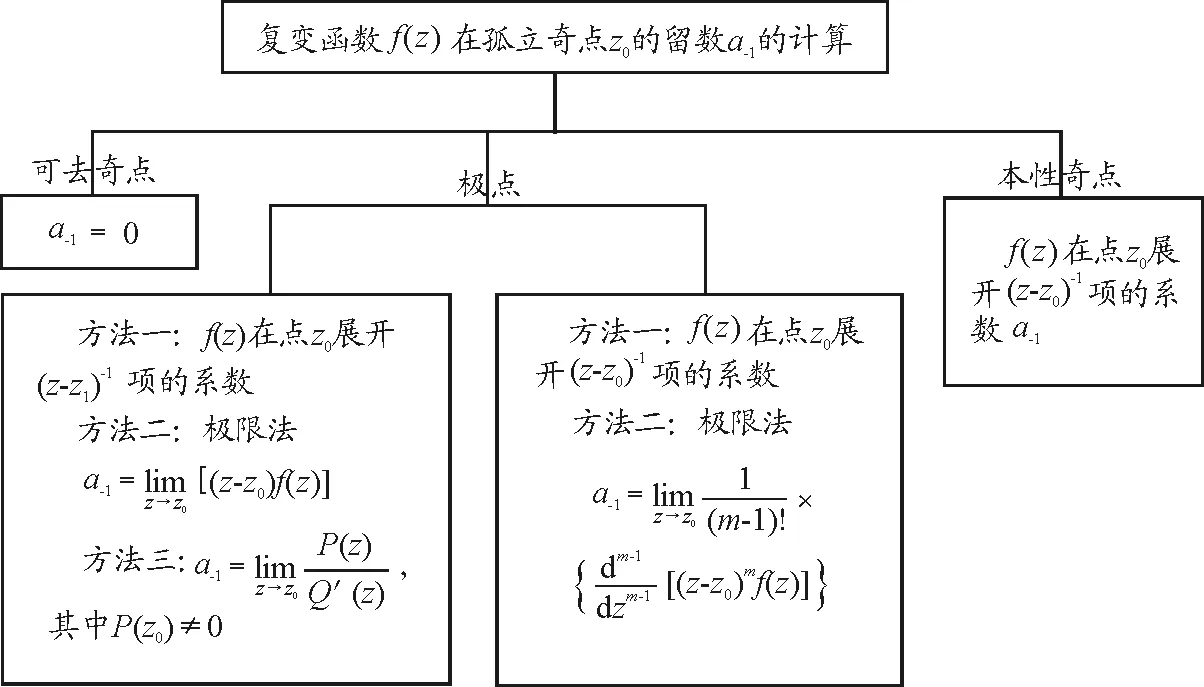
圖5 復變函數在孤立奇點留數的計算知識結構圖

2 數理方程部分

數理方程部分主要包括數理方程的建立和求解問題，對于這部分內容，發現學生在學習中主要的難點集中在定解問題的求解和部分二階常微分方程的求解方面．

2.1 定解問題的求解

關于定解問題的求解，最基本的方法是分離變量法，分離變量法主要適用于求解齊次泛定方程和齊次邊界條件的問題，在平時的教學中，發現學生對于分離變量法基本能夠掌握，而對于非齊次泛定方程和非齊次定解條件的定解問題，學生在學習時卻難以把握，如何分析具體如圖6所示(以波動定解問題為例)．

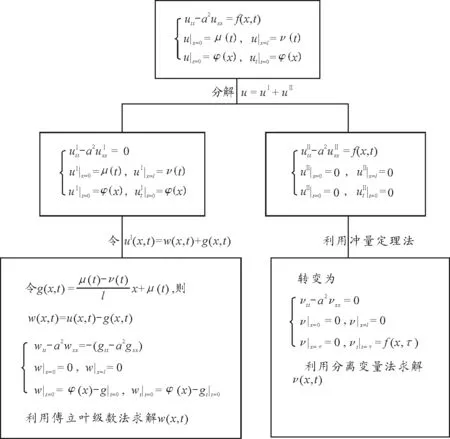
圖6 數學物理方程求解知識結構圖

2.2 二階常微分方程的求解

數學物理方程中定解問題的求解，在求解泛定方程的過程中很多定解問題都涉及到二階常微分方程的求解，一般的二階常微分方程求解在高等數學中已經學習過，在該部分出現比較多的是歐拉方程和施圖姆-劉維爾本征值問題，這兩個問題是求解泛定方程必須要解決的問題．

2.2.1 歐拉方程

歐拉方程式為

a1x2y″(x)+a2xy′(x)+a3y(x)=0

其中a1，a2和a3為常數，且a1≠0．歐拉方程的求解通常是令

x=et

然后將變系數常微分方程轉化為常系數二階微分方程

求解．

2.2.2 施圖姆-劉維爾本征值問題

在求解數學物理定解問題(波動問題、輸運問題以及穩定場問題)的過程中，這些問題在求解過程中都涉及到施圖姆-劉維爾本征值問題，關于這類問題的歸納主要如表1所示．

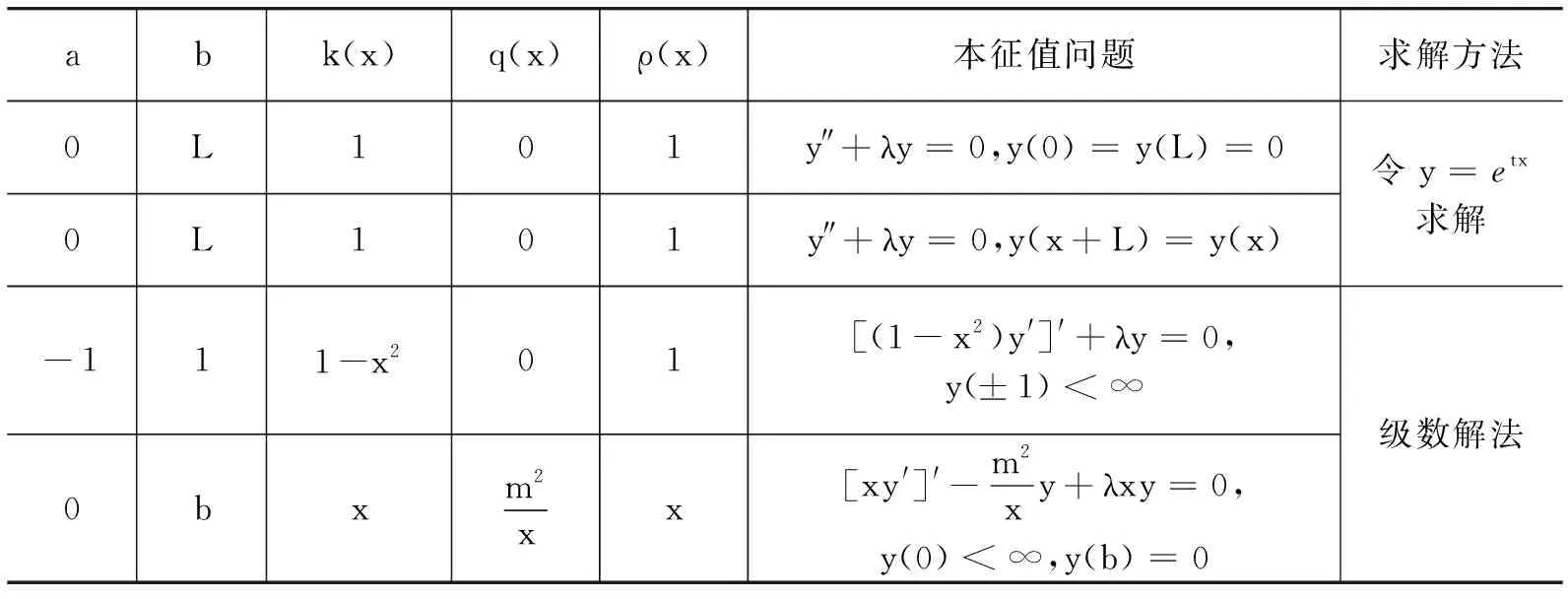
表1 施圖姆-劉維爾本征值問題知識結構

3 結論

數學物理方法是物理類專業一門重要的承上啟下的核心課程．合適的教學方法是高等教育發展一直推行的舉措，其中最基本的是對課程內容的把握．根據數學物理方法課程的特點以及教學實踐中的體會，本文主要針對學生難以掌握的知識點采用知識結構圖的方法，將復雜知識點分解為一系列簡單知識點來理解，進而找出其中需要掌握的關鍵知識點，以此幫助學生提高學習效率．