基于密度泛函理論計算的二次電子發射對放電等離子體特性的影響

汪 劍，鐘 安，戴 棟，朱明睿

(華南理工大學電力學院，廣東 廣州 510641)

低溫等離子體在能量轉換[1]、材料科學[2]、醫學[3]和許多其他領域[4]都受到了極大的關注，并逐漸顯示出巨大的潛力。隨著等離子體技術的新興應用，等離子體表面相互作用變得越來越復雜，這給等離子體基礎研究和進一步應用帶來了巨大挑戰。為了更好地調節低溫等離子體的放電參數并充分利用它，人們通過實驗和模擬研究了影響等離子體放電特性的因素。

在等離子體介質表面的物理和化學過程中，電介質層上積聚的表面電荷和離子誘導二次電子發射(SEE)是對等離子體放電產生影響的兩個重要物理過程。根據之前的工作，介質表面電荷會影響等離子體的時空特性[5]。Dong等人[6]和Boeuf等人[7]的研究結果表明，介質表面電荷將導致介質阻擋放電(DBD)空間模式的轉換。關于等離子體射流，Viegas等人[8]發現表面電荷會影響電場和電介質的電離波傳播。至于SEE，大量研究表明，它是影響放電特性的一個重要因素。為了探索SEE對等離子體特性的影響，已經建立并發展了相應的實驗和理論[9-11]。由于電子在電介質表面電荷的形成中起著重要作用，二次電子發射系數(SEEC)應與電介質表面電荷有關[5]。然而，一方面，表面電荷引入SEE過程分析等離子體特性變化的研究十分有限[12,13]。另一方面，前人的計算方法采用近似簡化，忽略了實際表面電荷和電子結構的影響，無法獲得表面電荷對SEE和等離子體特性相關變化的真實而準確的影響。例如，Yao等人[12]報道了氦DBD模型中二次電子發射系數與介質表面電荷之間的函數變化關系，并討論了對放電特性的相關影響。然而，他們使用的模型用能帶結構間隙中的簡化參數代替了表面電荷的影響，由于表面電荷對電子結構的改變[14]，這一計算模型無法準確反應SEE與表面電荷之間的關系。為了探索等離子體放電的實際動力學過程，迫切需要一種更精確的SEE過程計算方法。

本研究基于密度泛函理論和俄歇中和理論進行了分析計算，以研究氧化鎂(MgO)電介質的表面電荷對SEE的影響。在此基礎上，將計算得到的SEEC與表面電荷的關系函數代入流體模型，分析更精確的SEE過程對等離子體特性的相應影響。本文采用含氮摻雜的氦氣大氣壓介質阻擋放電(DBD)作為研究案例，并選擇正弦電壓作為激勵源。此外，zhang等人研究發現在削波電壓下放電殘留的表面電荷較少[15]。為了更直觀地分析二次電子發射過程考慮表面電荷積聚是否會對ADBD的時空特性產生影響，本文中引入削波電壓和正弦電壓進行對比[15-17]。

仿真結果進一步證實了介質表面電荷通過改變SEE過程極大地影響了放電等離子體的動力學行為。此外，引入真實表面電荷的SEEC計算方案保證了放電等離子體特性的準確探索，這為進一步研究在對表面過程敏感的廣泛物理場景中等離子體的動力學奠定了理論基礎。

1 DBD仿真模型介紹

使用COMSOL Multiphysics搭建了一個二維軸對稱模型，如圖1所示。

圖1 仿真模型Fig.1 simulation model

該模型寬為4 mm，長為10 mm，上下介質層厚度均為1mm，在介質層表面有一層MgO介質，如圖1所示。模型內部的圓柱形腔厚度為2mm，長為10 mm，腔內充滿溫度為300 K的常壓空氣。在此基礎上，在模型上極板施加幅值為1.5 kV、頻率為10 kHz的正弦激勵源。

本文使用的電壓波形有兩種：正弦電壓和削波電壓，其中削波波形是在前人研究的基礎上修正得來[15]。我們通過設置平頂階段的初始時刻t0來對初始正弦波形進行調制，調制后的波形如圖2所示。修正后的削波波形在正、負半周期之間保持對稱，每半周期平頂持續的時間為2t0，電壓幅值為1.5 kV、頻率為10 kHz。另一種施加電壓為正弦電壓，電壓幅值同樣為1.5 kV、頻率為10 kHz。

t/μs圖2 削波電壓波形Fig.2 Illustration of peak-leveled applied voltage

本文使用的二維DBD模型基于等離子體流體方程搭建而成，其中電子遷移等相關粒子參數通過玻爾茲曼方程解析，在遷移擴散近似下簡化為連續方程：

(1)

(2)

Γe=-μeneE-De?·ne

(3)

(4)

式中，ne和nε分別為仿真中的電子數密度和電子能量，初始值分別設置為2×106m3和3 eV。Гe和Гε分別表示電子通量和電子能量通量。源項Se表示由化學反應引起的電子密度凈變化率的源項，Sε是電子能量的源項，代表電子與重物質碰撞產生的能量增益或損失。E代表電場強度，E·Гe代表焦耳熱。μe表示電子遷移率[18-19]。

重粒子輸運受多組分輸運方程[19]控制

(5)

(6)

其中ρ是混合物的密度；ωk代表物種k的質量分數；Mn表示混合物的平均摩爾質量；Jk是質量分數為ωk的通量矢量，電荷量為zk；Sk表示重物質的源項。遷移率μk和擴散系數Dk是從之前的研究中得到的[20-21]。

表1 仿真模型中的表面反應Tab.1 Surface reaction in simulation model

2 MgO二次電子發射系數計算

2.1 DFT計算及俄歇中和理論

本文基于俄歇中和理論和密度泛函理論計算MgO二次電子發射系數[12,23-28]。

首先，基于第一性原理軟件VASP進行了DFT計算，計算中采用贗勢平面波方法和PBE泛函構建了MgO模型，其中晶胞的棱長a、b、c分別為a=b=c=2.976 97 ?，三組棱長之間的夾角α、β、γ分別為α=β=γ=90°。

對MgO結構進行優化時，布里淵區k點網格設置為11×11×11，平波截止能量為400 eV且高斯變換設置為0(ISMER=0)。計算態密度(DOS)時，布里淵區k點網格設置為22×22×22，ISMER=-5，進而分別得到Mg和O的分態密度和MgO的總態密度。最后進行真空能級計算時，MgO表面設置的真空寬度大于20 ?以防止垂直于表面方向上的各平行板之間存在相互作用[13,29]。

本文對二次電子發射過程的分析基于Hagstrumd勢能模型展開。由于文中考慮的大氣壓介質阻擋放電外施電壓較低，且氣隙內部離子能量較低，所以主要考慮離子自身的勢能(電離能)，入射離子的發射能量及發射方向在本文中暫不考慮[23,26]。

計算中主要考慮兩個主要因素，一個是不同的帶電離子在背景氣體中的作用，另一個是在介質表面上是否存在電荷積聚。具體的物理過程如圖3所示。

當正離子接近電介質表面時，價帶中的電子(電子A)在具有勢能Ei(S)的正離子的作用下被激發到真空水平，然后被正離子中和。中和過程中釋放的能量可以激發表面勢壘中的另一個束縛電子(電子B)達到真空水平，這是二次電子激發過程。俄歇中和理論包括兩種激發電子的方法：去激發與俄歇中和。其中，俄歇中和貢獻率占90%，因此在這項工作中，我們主要考慮俄歇中和的過程。

圖3 基于俄歇中和理論的二次電子發射過程Fig.3 SEE of Auger neutralization

如圖3所示，電介質中電子A和電子B的初始能量分別為ε1和ε2。在兩個電子被正離子激發之前，它們在電介質中的分布由導帶密度Nc(ε)和價帶密度Nv(ε)表征[13]。為了確定金屬中受激電子的分布，在離子撞擊金屬介質之前就要考慮電子各種能量分布的可能性，引入俄歇變換如式(8)所示。當電子受到離子的激發之后，其能量分布可以用方程(7)來描述[13,26]。當電子被激發時，受激發的電子根據其自身的速度矢量具有不同的逃逸概率Pe(εk)[13,26]。當電子具有足夠的能量逃逸出電介質表面時，就成為了“逃逸電子”。

εk=ε1+ε2-E0+EiNk(εk)=

(7)

T(ε)=

(8)

式(8)中ε和Δ含義如下：

Δ=ε1-ε

(9)

(10)

N0(εk)=Nk(εk)Pe(εk)

(11)

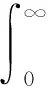
(12)

逃逸電子的分布N0(εk)可以簡單的通過對激發態電子的分布和逃逸概率進行乘積得到，如式(11)所示。最后對式(11)進行積分，可以得到二次電子發射系數γ，如式(12)所示。上文提到的諸如Nc(ε)和Nv(ε)等變量均來自于DFT模型，其物理含義如表2所示[13,26]。

表2 符號變量含義Tab.2 Symbolic variable

進一步地，使用MATLAB軟件對式(7)～(12)進行編程，將通過DFT軟件計算得到的MgO的電子結構參數代入到程序中，即可得到二次電子發射系數。

2.2 表面電荷對二次電子發射系數的影響

相比于之前的學者利用簡化參數或簡化方程模擬介質表面電荷的計算方法[12-13]，本研究使用了一種更精確的方法計算介質表面有電荷積聚的SEEC。通過在金屬表面設置電子來調節表面電位以模擬介質表面的電荷積聚。該方法被廣泛應用于等離子體催化領域，已被證明是可靠的[30]。

在DFT模型中，表面電荷密度與電子和能級的態密度有關，σ=eNeldEe，其中e是基本電荷，Ne是陷阱密度，dEe是被占據電子陷阱的能量帶寬，l是設置為1×10-10m的陷阱深度[12-13]。在下文的計算中，通過改變介質表面電子e的數量模擬不同表面電荷積聚量σ。進而計算此時的態密度和真空能級，在此基礎上得到相應的二次電子發射系數，如表3所示。

進一步地，基于表3的數據使用插值法擬合出表面電荷密度和二次電子發射系數之間的函數關系，將其代入到流體模型中進行計算。

在下文的仿真中，使用控制變量法對比二次電子發射系數不考慮表面電荷影響、為定常數的模型(UN-CONS模型)和二次電子發射系數考慮表面電荷影響的模型(CONS模型)，兩者放電時空特性的區別并分析其原因。上述兩個模型除二次電子發射系數不同之外，其余參數不變。

σ/(μC/m3)

σ/(μC/m3)圖4 He+和離子在UN-CONS模型和CONS模型的二次電子發射系數對比Fig.4 The comparison of SEEC of He+ and ions between the UN-CONS simulation and the CONS simulation

由圖4可知，在UN-CONS模型中，當二次電子不考慮表面電荷影響時為定常數。在CONS模型中，二次電子發射系數在表面積聚負電荷時增加。在表面積聚電荷正電荷時減少，因為此時介質內部靠近真空層的電子會大大減少進而使得電子更難逃逸介質表面[23,26]。

表3 非定常二次電子發射系數計算值Tab.3 calculated values of real-time change secondary electron emission coefficient

3 仿真結果及分析

本節通過比較削波電壓和正弦電壓下兩個模型的電流波形以及電子空間分布，以分析SEE過程中是否考慮介質表面電荷對放電時空特性會產生什么影響以及背后的機制。圖5和圖6比較了正弦電壓和削波電壓下CONS模型和UN-CONS模型的電流幅值以及放電峰值相位，t1-t8為兩種外施電壓下放電達到穩態時的電流峰值時刻。

可以發現，考慮介質表面電荷的SEE過程對正弦電壓下的放電電流波形有一定的影響。放電峰值時刻相位提前，電流幅值減小。然而在削波電壓下，放電相位和電流幅值變化不大。此外，可以看出，第一次主放電并不明顯，因為第一次放電的輝光結構被破壞，種子電子數減少。然而，第二主放電顯著增強，這與Zhang等人[31-32]的研究結果一致。電流波形的變化以及放電峰值時刻提前與表面電荷之間的關系可通過以下方程式(12)～(15)[31,32]進行簡單分析：

t/10-4 s圖5 正弦電壓下UN-CONS模型和CONS模型的電流幅值對比Fig.5 The comparison of current amplitude of the UN-CONS simulation and the CONS simulation under sinusoidal voltage

t/10-4 s圖6 削波電壓下UN-CONS模型和CONS模型的電流幅值對比Fig.6 The comparison of current amplitude of the UN-CONS simulation and the CONS simulation under peak-leveled applied voltage

Egdg=Vg

(13)

ε0εrE1-ε0Eg=ρs1

(14)

ε0Eg-ε0εrE2=ρs2

(15)

E1db+Egdg+E2db=Vamsinφm

(16)

式中，Eg表示放電擊穿時刻氣隙中的電場強度，dg表示氣隙厚度，Vg表示擊穿時刻的氣隙電壓；E1和E2分別為擊穿時刻電源電極側附近電介質層中的電場強度和接地側附近電介質層中的電場強度；ρs1和ρs2是擊穿時刻氣隙上下壁上的電荷密度，φm是擊穿時刻的相位。

通過將等式(12)～(15)代入(16)，可以得到：

φm=arcsin

(17)

提取方程(16)中所示的間隙電壓Vg和上下層表面電荷密度ρs1，ρs2，以分析潛在的物理機制(圖7)。

d/mm圖7 正弦電壓下峰值放電時刻UN-CONS模擬與CONS模擬的|ρs1|+|ρs2|對比Fig.7 The comparison of |ρs1|+|ρs2| between the UN-CONS simulation and the CONS simulation under sinusoidal voltage at peak discharge moment

t/10-4 s圖8 正弦電壓下峰值放電時刻UN-CONS模擬與CONS模擬的電勢對比Fig.8 The comparison of potential between the UN-CONS simulation and the CONS simulation under sinusoidal waveform at peak discharge moment

根據方程式(16)，Vg、ρs1和ρs2是影響放電相位的主要參數。如圖7所示，CONS模型的|ρs1|+|ρs2|遠大于UN-CONS模擬。另一方面，CONS模型和UN-CONS模型的氣隙電壓幅值在圖8中幾乎相同。可以推測在正弦電壓下，當|ρs1|+|ρs2|項較大時，φm較小，相位提前，這與前面的分析一致。

為了進一步分析電流波形幅值變化的影響因素，比較了正弦電壓和削波電壓下穩態放電周期內的空間電荷密度分布圖，如圖9和圖10所示。

t/10-4 s圖9 正弦電壓下UN-CONS模型與CONS模型空間電荷密度對比Fig.9 The comparison of space charge density between the UN-CONS simulation and the CONS simulation under sinusoidal voltage

t/10-4 s圖10 削波電壓下UN-CONS模型與CONS模型的空間電荷密度對比Fig.10 The comparison of space charge density between the UN-CONS simulation and the CONS simulation under peak-leveled applied voltage

圖9是正弦波電壓下CONS模擬和UN-CONS模擬第三放電周期的空間電荷密度比較。從圖9(a)和圖9(b)可以看出，當SEE過程與介質表面電荷相關時，CONS模擬的種子電子密度在預電離階段較高。較高的種子電子密度降低了后續放電峰值的電流幅值，放電階段提前[33]。當種子電子密度較高時，放電提前熄滅而未充分發展，導致氣隙電壓較弱[33]。

另一方面，電子雪崩過程中電子密度ne的函數關系如等式(17)[31-32]所示：

其中ne0表示種子電子密度，α表示碰撞電離率：

(18)

式中，p表示排出氣體的氣壓，E表示場強，A和B為湯森系數。

理論上，放電實現自我維持所需的條件是：

(19)

方程式(19)僅適用于直流湯森放電，但當γ擴展到為下一次放電提供二次電子的所有過程系數時，它可用于DBD。在這種情況下，預電離階段的種子電子密度增加相當于γ值的增加，因此放電將發生在α較小的時候。然而，α和E正相關。在擊穿過程中，隨著種子電子數的增加，氣隙中的場強將受到抑制。因此，在較低場強下發生的放電具有較小的電流幅值。

圖10是削波電壓下CONS模擬和UN-CONS模擬中的空間電荷對比圖。從該圖可以看出，當在二次電子發射過程中考慮介質表面電荷時，空間電荷密度在峰值放電時刻略有降低，放電相位變化不大，這與圖5中的電流波形基本一致。

從圖5和圖9可以發現，當施加的電壓波形為正弦時，表面電荷積聚對二次電子發射過程有較大影響。當外加電壓為削波電壓時，無論SEE過程中是否考慮介質表面電荷，它對DBD的時間和空間特性幾乎沒有影響。造成這個現象的原因是削波電壓下的放電過程中，介質表面殘留的表面電荷較少。為更直觀地觀察此現象，我們在圖11中畫出了削波電壓和正弦電壓下峰值放電時刻表面電荷密度對比。

從圖11可以看出，與正弦電壓下相比，削波電壓下放電峰值時刻的表面電荷密度大大降低。由此可見，我們引入削波電壓作為比較，的確可以幫助我們更直觀地揭示表面電荷不僅會對二次電子發射系數產生影響，并且會進一步影響ADBD的時空特性，之前的研究已經發現了類似的現象[17]。

為進一步分析考慮表面電荷積聚的二次電子發射過程對DBD時空特性的影響，我們在圖12和圖13中畫出了放電峰值時刻的電子密度分布圖，圖中的t1到t8對應圖5和圖6中放電峰值時刻的時間點。

上圖是正弦電壓下放電峰值時刻的電子密度空間分布圖，可以發現當二次電子發射過程不考慮表面電荷積聚時，放電出現明顯的主放電柱，此時是不均勻放電。當二次電子發射過程考慮表面電荷積聚時，放電變得更加彌散，此時的放電為均勻放電。

d/mm圖11 削波電壓和正弦電壓下峰值放電時刻表面電荷密度對比Fig.11 The comparison of surface charge density at peak discharge moment under peak-levelled applied voltage and sinusoidal voltage

圖12 正弦電壓下CONS模型和UN-CONS模型的放電峰值時刻電子密度對比Fig.12 The comparison of electron density at peak discharge time between cons model and un-cons model under sinusoidal voltage

圖13 削波電壓下CONS模型和UN-CONS模型的放電峰值時刻電子密度對比Fig.13 The comparison of electron density at peak discharge time between cons model and un-cons model under clipping voltage

上圖是削波電壓下電子密度的空間分布圖，可知在削波電壓下二次電子發射過程是否考慮表面電荷積聚對電子密度分布影響不大。但是二次電子發射過程考慮表面積聚的影響之后，電子密度依舊下降，放電同樣變得更加彌散。造成該現象的原因是，當表面積聚電荷為負電荷時，二次電子發生系數增大使得電子通量增加，進而使得放電更加均勻、彌散[12]。

綜上所述，是否考慮表面電荷積聚不僅對二次電子發射系數(SEEC)有影響，也會進一步對放電形式產生一定的影響，使得放電變得更加彌散。正弦與削波電壓激勵下放電過程的對比進一步驗證了本研究采用的DFT計算方案的有效性。

3 結論

本文研究了介質表面電荷控制的SEE過程對DBD放電特性的影響。使用了一種更精確的方法來計算SEEC，該方法通過DFT模型中的計算來考慮實際的表面電荷效應，并將得到的SEEC代入二維流體仿真模型中進行計算分析。此外，為了更直觀地分析電介質表面電荷在二次電子發射過程中的作用，我們引入了在放電期間攜帶少量表面電荷的削波電壓，作為與正弦電壓的比較。

模擬結果表明，在二次電子發射過程中考慮介質表面電荷時，DBD放電相位提前，電流幅值減小，并進一步影響放電特性。本研究發現介質表面電荷會影響SEE過程，并進一步改變放電等離子體的演化過程。本研究引入了更精確的SEEC計算方案，確保了DBD時間和空間特性的精確探索，這為進一步研究等離子體在廣泛的物理過程中對表面過程敏感的動力學問題奠定了理論基礎。