循環荷載作用下粉砂巖疲勞流變損傷模型研究

苗勝軍，楊鵬錦，王 輝，梁明純，王亞欣

(1. 北京科技大學城市地下空間工程北京市重點實驗室，北京 100083；2. 北京科技大學土木工程系，北京 100083)

巖體工程在施工及運營階段經常會受到循環荷載作用，如地下硐室的爆破開挖與支護、水庫周期性蓄水和放水、巖鹽儲氣庫的注氣和采氣過程等[1]。定量化研究循環荷載作用下巖石的疲勞損傷特性及其變形演化規律，對巖體工程長期穩定性評價具有重要的理論指導意義。

國內外學者對巖石的疲勞變形特性開展了大量的研究。Bagde等[2?3]通過疲勞試驗，發現砂巖疲勞強度隨著頻率和應力幅值的增加而趨于減小；Jind?ich等[4]定性地研究了不同幅值、不同頻率循環荷載下砂巖的流變特性，發現平均應力和幅值對巖石變形特征的影響比頻率更為顯著；Rashid等[5?6]對比分析了花崗巖和砂巖的疲勞破壞機制。楊永杰等[7]認為單軸循環荷載下煤巖體的疲勞強度“門檻值”不超過其單軸抗壓強度的81%；葛修潤等[8]和章清敘等[9]發現巖石循環加卸載過程中軸向不可逆變形可劃分為初始變形、等速變形和加速變形3個階段；郭印同等[10]通過鹽巖疲勞試驗研究發現，改變上限應力和平均應力會顯著影響疲勞破壞的進程；盧高明等[11]發現圍壓對軸向變形有一定強化作用，且變形比強度更適合作為巖石疲勞破壞的依據。

循環荷載作用下，巖石變形破壞表現出顯著的時間效應，黃明等[12]基于巖石流變特性建立了廣義Kelvin-Voigt體的正弦加載蠕變模型；許宏發等[13]將損傷變量引入累積塑性應變中，推導了高周期和低周期循環荷載作用下巖石軸向塑性應變方程；王軍保等[14]基于低頻循環荷載蠕變試驗，推導了循環荷載下Burgers模型的軸向蠕變方程；郭建強等[15]將疲勞簡化為恒定等效應力下的蠕變過程，建立了巖石的疲勞本構模型；李永輝等[16]將西原模型中線性黏性元件替換為含疲勞參數的非線性黏性元件，建立了循環荷載下改進的西原疲勞模型；劉斌等[17]基于應力耗散原理建立了非線性黏壺力學元件，推導獲得循環荷載下應變隨時間變化的本構方程。

綜上，將循環荷載簡化為恒定應力來建立流變本構模型的方法雖然可以較好地擬合試驗結果，但不夠嚴謹，物理意義模糊；此外，當前鮮有將損傷變量引入流變模型描述循環荷載下巖石疲勞破壞加速流變階段的研究。

因此，本文根據正弦波循環荷載作用下粉砂巖疲勞變形破壞試驗結果，在Burgers模型的基礎上引入黏塑性損傷元件構建巖石疲勞流變損傷模型，并以正弦波循環荷載為例，將應力-時間函數替換流變微分本構方程中的恒定應力，推導循環荷載作用下巖石一維、三維非線性流變損傷方程。最后，驗證了模型的合理性和適用性，分析了不同上限荷載下流變本構模型參數的演化規律，并討論了巖石疲勞壽命的預測方法。

1 粉砂巖疲勞試驗及結果分析

1.1 正弦波循環荷載下粉砂巖疲勞試驗

本次試驗所選取的粉砂巖主要礦物成分為石英、斜長石、云母類和整柱石。如圖1所示，按照國際巖石力學試驗標準將巖樣加工成?50 mm×100 mm的圓柱體，試樣上、下端面的不平整度控制在 ±0.02 mm以內，并根據超聲波速測試剔除了離散性較大的試樣。

圖1 巖石試樣Fig. 1 Rock samples

本次試驗采用的MTS815巖石液壓伺服力學系統可施加頻率為0.01 Hz～5 Hz的軸向正弦波、三角波、矩形波、斜波、隨機波和組合波荷載。通常，正弦波形式的循環荷載更接近巖體工程受到的動力擾動模式，因此，本次試驗對試件施加正弦波循環荷載。

應力路徑如圖2所示。圖中σ(t)為時間t時的應力值；σmin為循環荷載下限應力，σmax為循環荷載上限應力；平均應力a=(σmax+σmin)/2，應力幅值b=(σmax?σmin)/2 ；T為循環周期。

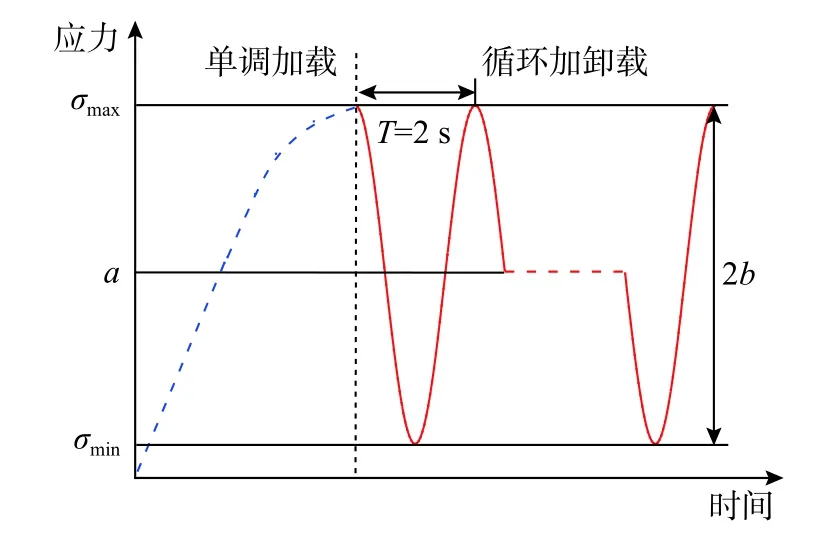
圖2 應力路徑Fig. 2 Path of stress loading and unloading

因此，正弦波應力函數可表示為：

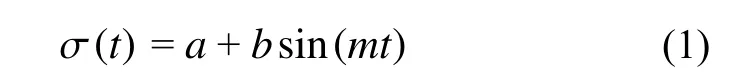
式中，m=2π/T。

為選擇合適的循環荷載上限，首先開展了5組單軸壓縮試驗，粉砂巖的單軸抗壓強度和彈性模量均值分別為34.76 MPa和5.03 GPa。根據粉砂巖單軸壓縮強度特征，循環荷載上限設定為30 kN、40 kN、45 kN、55 kN、60.5 kN、61 kN、61.5 kN、63 kN、65 kN，循環荷載下限為5 kN，循環頻率為0.5 Hz，試驗方案及結果見表1。

表1 試驗方案及結果Table 1 The scheme and results of test

1.2 不同循環荷載上限下粉砂巖疲勞變形特性

不同循環荷載下粉砂巖應力-應變曲線(以上限荷載30 kN、45 kN、61 kN為例)如圖3所示，由表1和圖3可知：上限荷載為55 kN時，循環加卸載15 000次后試樣仍未發生疲勞破壞，由此可初步推斷正弦波循環荷載作用下粉砂巖的疲勞強度在28.06 MPa～30.88 MPa(55 kN～60.5 kN)，約為單軸壓縮強度的80%～90%。當上限荷載高于60.5 kN時，試件發生疲勞破壞，且破壞時的軸向變形量與單軸壓縮應力-應變全過程曲線峰后區在循環載荷上限位置的變形量相當。

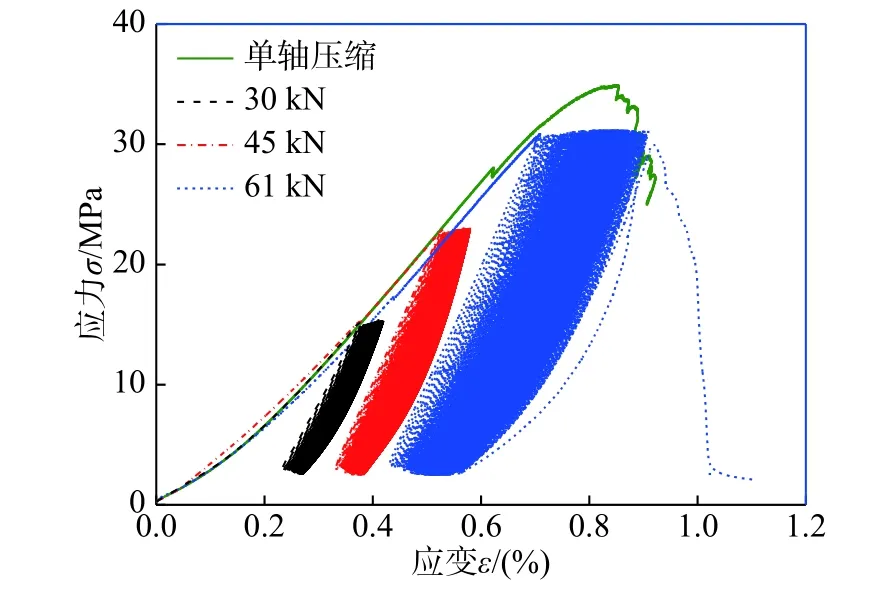
圖3 不同上限荷載下粉砂巖軸向應力-應變曲線Fig. 3 Axial stress-strain curves of siltstone under different upper limits of cyclic loading

圖4為不同上限荷載下粉砂巖平均應變(上限應變與下限應變的平均值)隨時間演化曲線。可以看出，當上限荷載低于疲勞強度時，粉砂巖軸向應變-時間曲線均表現為初始變形、勻速變形2階段；循環荷載上限高于疲勞強度時，軸向應變-時間曲線呈典型的初始變形、勻速變形和加速變形3階段演化特征。

圖4 粉砂巖平均應變隨時間演化曲線Fig. 4 Time evolution curves of average strain of siltstone

分析認為，巖石是一種含有天然裂隙、孔隙的非均質材料，試驗初始階段，巖石內部晶格缺陷、微裂紋、軟弱界面在循環荷載作用下不斷閉合，應變量顯著增加；多次循環后，巖石原生缺陷逐漸壓密，變形進入勻速階段，應變量表現為隨時間緩慢勻速增加；當循環荷載上限超過疲勞強度，巖石應變量到達某一值時，內部微裂紋不斷的擴展貫通，變形進入加速階段，巖石損傷發育表現顯著并發生疲勞破壞；而當循環荷載上限低于疲勞強度時，循環往復的加卸載作用無法使巖石內部微裂紋進一步大量萌生擴展，疲勞壽命表現為無窮大。

2 循環荷載下巖石疲勞流變損傷模型

根據粉砂巖的疲勞變形規律，構建巖石疲勞流變損傷模型，與試驗相對應，采用正弦波應力函數替換流變微分本構方程中的恒定應力，并推導模型一維和三維非線性流變損傷方程，具體過程如下。

2.1 循環荷載下Burgers流變模型

2.1.1 循環荷載下Maxwell體流變方程

Maxwell體由一個虎克體和一個牛頓體串聯組成，其流變微分本構方程為：

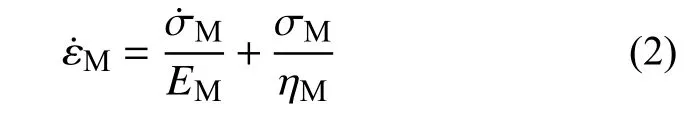
式中：σM、EM和ηM分別為Maxwell體的應力、彈性模量和黏性系數；ε˙M和σ˙M為Maxwell體的應變和應力對時間t的一階導數。

正弦波循環荷載下Maxwell體的流變微分本構方程可轉變為：

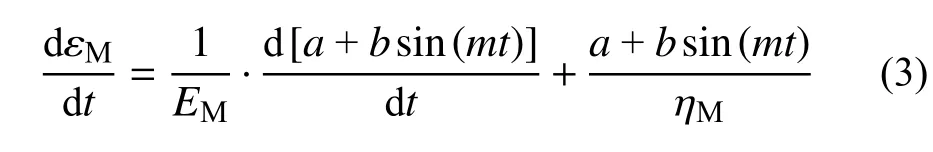
對式(3)兩端進行積分，可以得到正弦波循環荷載作用下Maxwell體的流變方程：

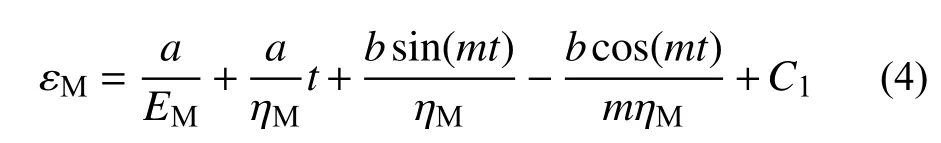
式中，C1為積分常數。當t=0時，εM=0，則：

將式(5)代入式(4)，可得：

2.1.2 循環荷載下Kelvin體流變方程

Kelvin體由一個虎克體和一個牛頓體并聯組成，其流變微分本構方程為：

式中：εK、σK、EK和ηK分別為Kelvin體的應變、應力、彈性模量和黏性系數；ε˙K為Kelvin體的應變對時間t的一階導數。

正弦波循環荷載下Kelvin體的流變微分本構方程可轉變為：

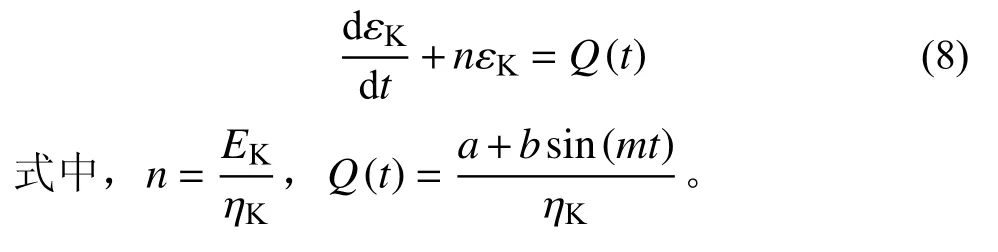
解式(8)的一階線性微分方程，可得正弦波循環荷載作用下Kelvin體的流變方程：

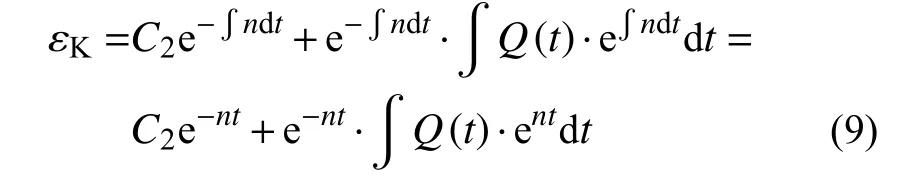
式中，C2為積分常數，其中：

對式(10)中的∫sin(mt)·entdt進行二次分部積分，則：

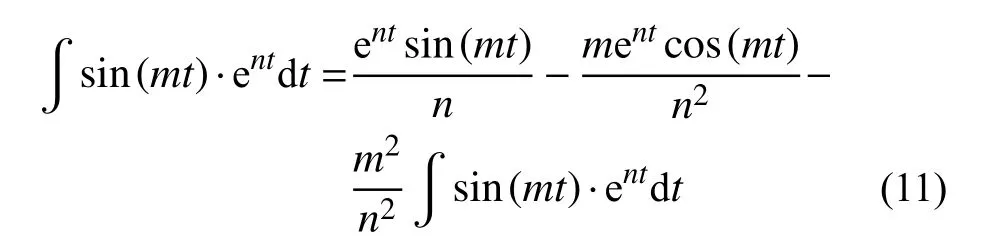
進一步整理化簡，可得：

研究區屬于寒溫帶濕潤季風氣候。其特點是冬長夏短，春秋相連，低溫濕潤，日照少。冬季長達9個月（平均氣溫<10℃），最低氣溫為-58℃，最高氣溫達到40℃，降水集中在7、8月份，年降水量在450～550 mm，凍結期在7個月以上；9月底至第2年的5月初為降雪期，降雪厚度一般在20～40 cm；年均日照為2 594 h，無霜期90 d左右。

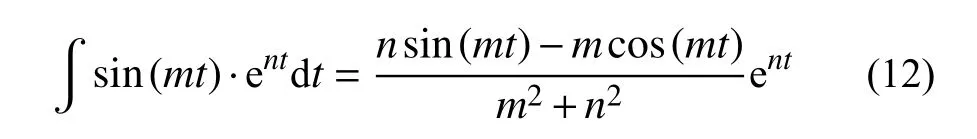
將式(10)、式(12)代入式(9)，得：

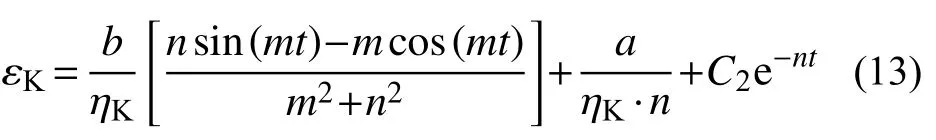
當t=0時，εK=0，則：

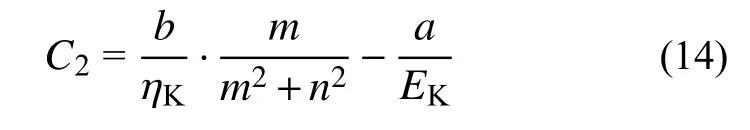
將式(14)代入式(13)，可得：

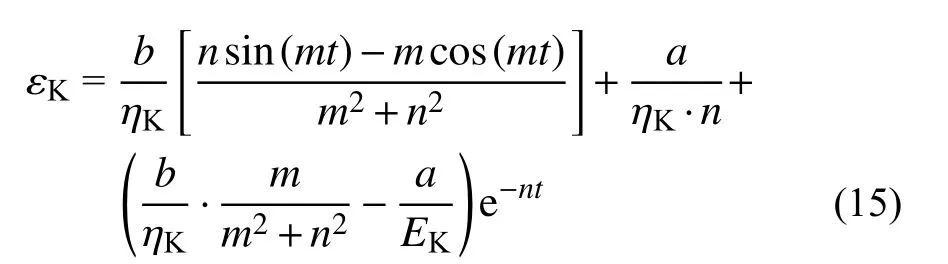
2.2 循環荷載下非線性黏塑性損傷元件

為了準確地描述循環荷載下巖石的疲勞破壞規律，如圖5所示，引入一個非線性黏塑性損傷元件來描述循環荷載作用下巖石加速流變階段。

圖5中，σS為巖石疲勞強度；εa為應變閾值，用于判斷巖石進入加速流變階段的應變狀態；ηVP和D分別為非線性黏性損傷元件的黏性系數和損傷變量。當循環荷載上限應力σmax≤σS時，非線性黏塑性損傷元件不起作用，巖石不會發生加速流變；當循環荷載上限應力σmax>σS且ε>εa時，黏性損傷元件啟動，巖石進入加速流變階段。

圖5 非線性黏塑性損傷元件Fig. 5 Nonlinear viscoplastic model for damage

基于Lemaitre應變等效假設[18]，將損傷變量引入牛頓體，則非線性黏性損傷元件流變微分本構關系為：

式中，ε˙VP為非線性黏性損傷元件應變εVP對時間t的一階導數。根據Kachanov[19]流變損傷理論，巖石的流變損傷變量隨時間的推移呈負指數函數增長，因此本文引入考慮時間效應的損傷變量：

式中，α為巖石損傷指數。則式(16)可轉化為：

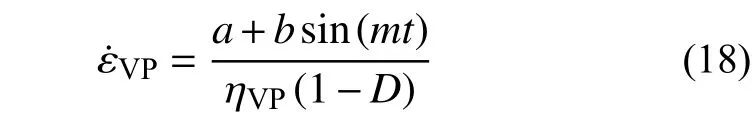
對式(18)進行積分，可得正弦波循環荷載下非線性黏塑性損傷元件的流變方程：

式中，C3為積分常數。當t=0時，εVP=0，則：

將式(20)代入式(19)，可得：

2.3 巖石疲勞流變損傷模型一維流變方程

根據以上分析，如圖6所示，在Burgers模型的基礎上串聯非線性黏塑性損傷元件，構建正弦波循環荷載作用下巖石非線性流變損傷模型。

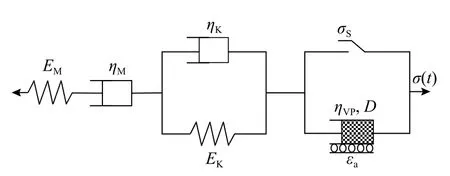
圖6 疲勞流變損傷模型Fig. 6 Fatigue rheological damage model

根據模型串并聯關系可以得到巖石流變模型的一維流變微分本構方程：

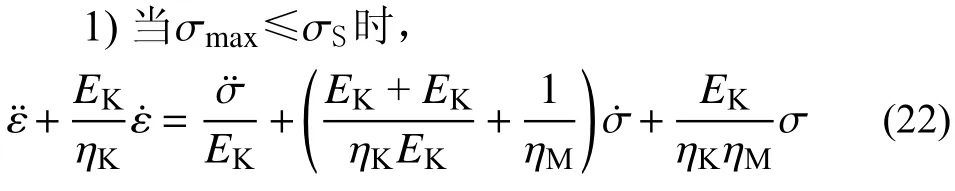
2)當σmax>σS且ε>εa時，

根據疊加原理可以得到正弦波循環荷載作用下巖石的一維流變損傷方程：

1)當σmax≤σS時，

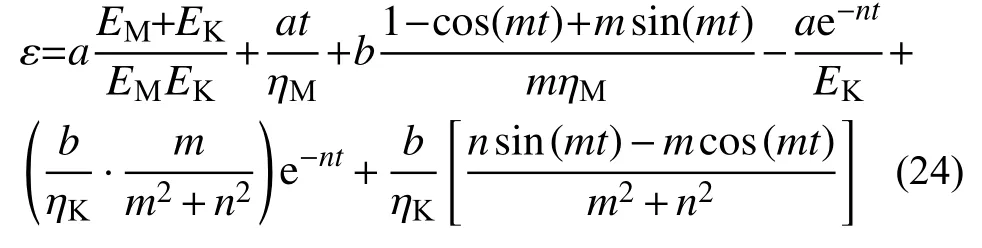
2)當σmax>σS且ε>εa時，

2.4 巖石疲勞流變損傷模型三維流變方程

三維應力狀態下，應力張量σij通常基于彈塑性理論分解為偏應力張量和球應力張量，流變方程則可通過類比法由一維流變模型導出。疲勞損傷流變模型的總應變為：

式中：Sij為偏應力張量；δij為Kronecker張量；K1為體積模量；σm為平均應力；N=G2/H2；G1、G2為三維剪切模量；H1、H2、H3為三維黏滯系數。

循環加卸載條件下軸向偏應力和平均應力可表示為：

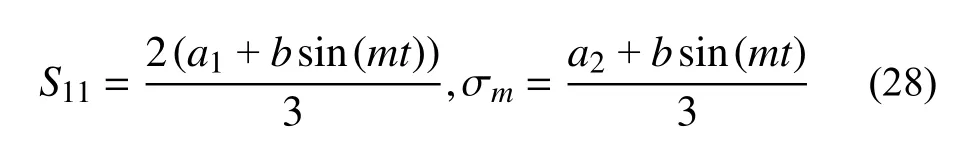
式中，a1=a?σ3，a2=a+2σ3。

根據一維流變本構方程的積分求解方法，可推導獲得三維應力狀態下軸向疲勞流變損傷方程：

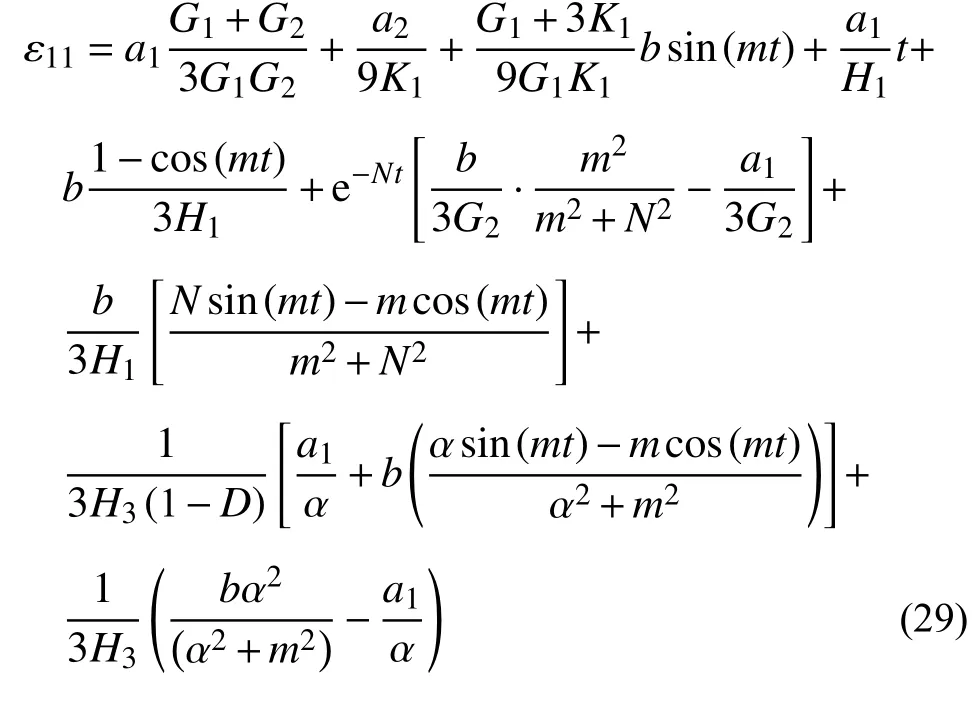
3 巖石流變損傷模型驗證及參數分析

3.1 非線性流變損傷模型適用性驗證

由式(25)和式(29)可知，一維狀態下模型共有EM、EK、ηM、ηK、α、ηVP和εa這7個參數；三維狀態下模型共有K1、G1、G2、H1、H2、H3、α和εa這8個參數。通過Origin軟件里的非線性擬合功能Fitting Function Organizer，編寫流變方程擬合程序，然后采用Analysis-Fitting-Nonlinear Curve Fit進行數據擬合，為了避免因參數過多和初值選取不當造成擬合不收斂或陷入局部最優，采用Levenberg - Marquardt法進行迭代計算模型各參數的理論值，然后代入流變損傷方程可獲得循環荷載作用下巖石流變損傷的理論曲線。

試驗采用的粉砂巖的疲勞強度值在28.06 MPa和30.88 MPa之間，因此，取二者平均值29.47 MPa作為本次一維流變模型擬合的疲勞強度值σS。以上限荷載45 kN和61 kN為例，粉砂巖試驗結果與理論曲線對比如圖7所示，一維非線性流變損傷模型參數見表2。為了驗證三維狀態下流變損傷模型的適用性，選用文獻[11]中與本次試驗粉砂巖力學性質相近的黃砂巖試驗數據進行擬合。文獻[11]開展了圍壓為5 MPa、10 MPa、20 MPa的黃砂巖軸向循環加卸載試驗，試驗結果和理論曲線對比與模型參數分布如圖8和表3所示。結果表明，一維和三維狀態下理論曲線與試驗結果的吻合度較好，說明本文建立的流變損傷模型不僅可以精確反映巖石的衰減流變和穩態流變，還可以準確地描述上限荷載高于疲勞強度時的加速流變，具有較好的適用性。

表3 三維流變模型參數擬合結果Table 3 Parameters of three dimensional rheological model

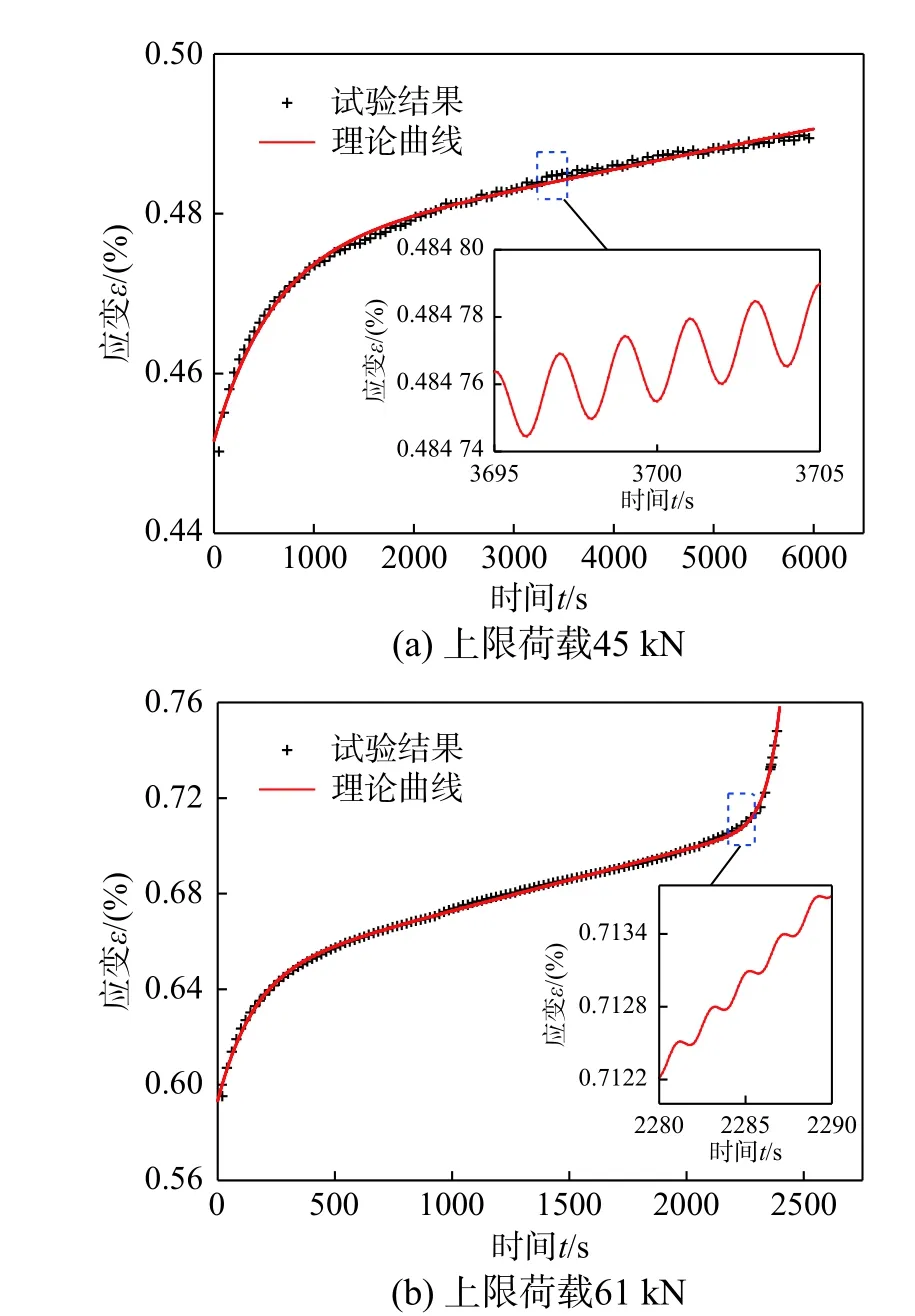
圖7 粉砂巖理論曲線與實驗結果Fig. 7 Comparison between theoretical curve and test results of siltstone

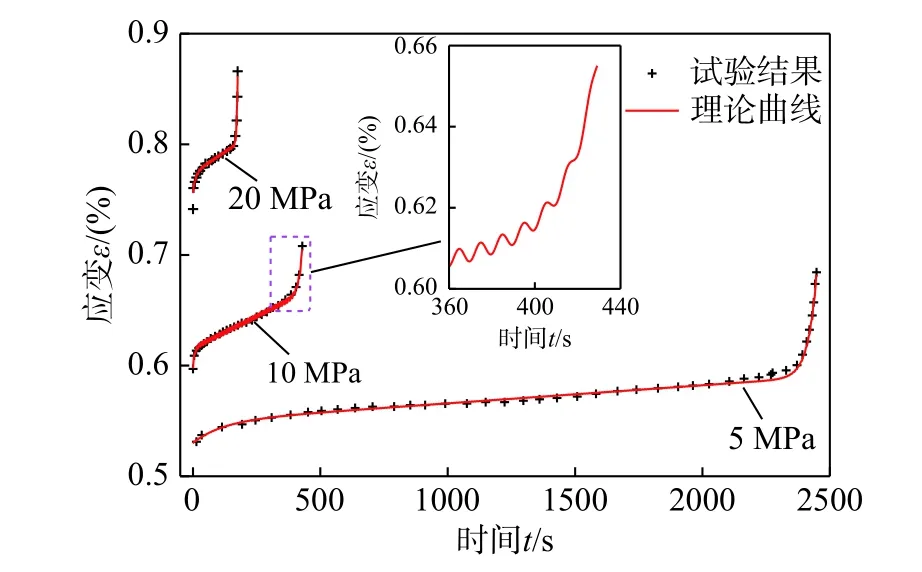
圖8 圍壓5 MPa、10 MPa、20 MPa時理論曲線與實驗結果Fig. 8 Comparison between theoretical curves and test results at confining pressure of 5 MPa、10 MPa、20 MPa

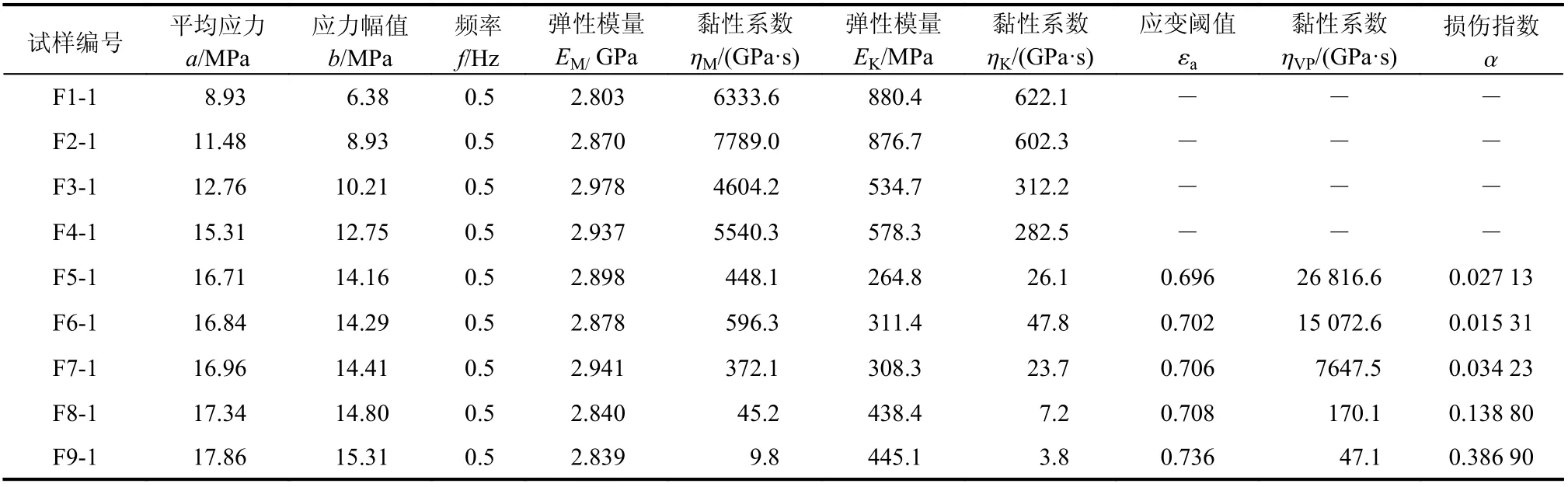
表2 一維流變模型參數擬合結果Table 2 Parameters of one dimensional rheological model

3.2 巖石疲勞損傷流變全過程定量化分析

3.2.1 上限荷載對衰減流變階段的影響

Kelvin體是由虎克體和牛頓體并聯形成，牛頓體推遲了虎克體的彈性變形，流變特征表現為衰減流變。因此選取弛豫時間τ表示Kelvin體彈性變形的推遲時間，根據模型性質可將τ定義為：

將式(30)代入Kelvin體流變方程中可知，當t=τ時：

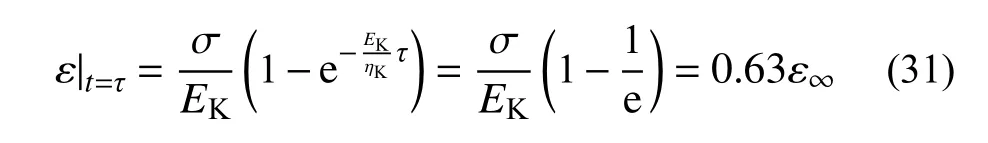
式中，ε∞為流變達到穩定狀態的最終變形，推遲時間為衰減流變達到穩定變形所經過時間的63%。Kelvin體系數n 和弛豫時間τ互為倒數，n越大，τ越短，穩定流變階段歷時越短；n越小，τ越長，由衰減流變過渡到穩態流變階段所需的時間越長。

從圖9不同上限荷載下粉砂巖Kelvin體系數n 和弛豫時間τ的演化曲線可以看出，Kelvin體系數n 和弛豫時間τ隨著上限荷載的增加分別呈非線性指數型增加和減少，說明循環荷載對粉砂巖原生裂隙和孔隙的壓密作用顯著，且上限荷載越大，對粉砂巖壓密作用的時效性越顯著。

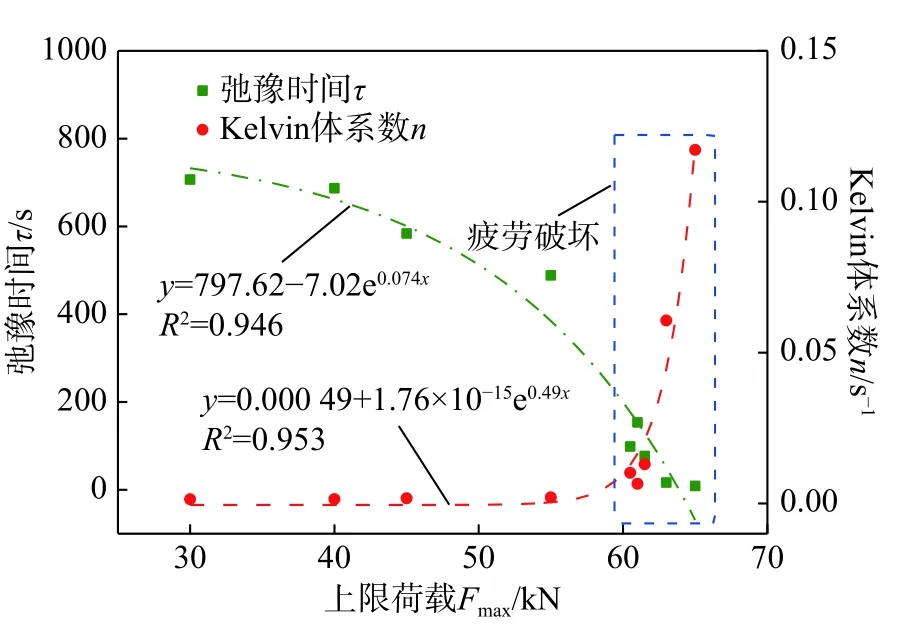
圖9 Kelvin體系數n 和弛豫時間τ的演化曲線Fig. 9 Evolution curves of nand τ under different upper limit of cyclic loading

3.2.2 上限荷載對穩態流變階段的影響

循環荷載作用下，巖石內部原生缺陷壓密和微裂紋萌生擴展兩種效應即相互對立，又同時存在，是一個交互作用的過程[21]。巖石的穩態流變速率可根據循環荷載平均應力a和Maxwell體黏性系數ηM的比值計算獲得。如圖10所示，穩態流變速率隨著上限荷載的增加呈非線性指數型增大。上限荷載較低時，巖石內部微結構以壓密為主，穩態流變階段微裂紋擴展速度緩慢；當上限荷載大于疲勞強度時，微裂紋萌生、擴展占據主導地位，巖石發生加速流變破壞，穩態流變速率顯著增加，約為上限荷載低于疲勞強度時的20倍～1300倍。

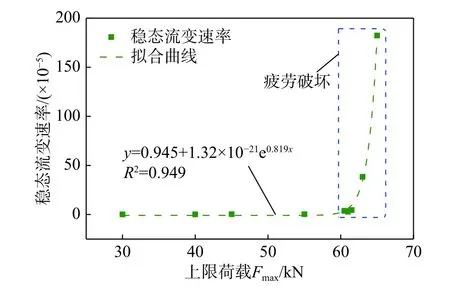
圖10 穩態流變速率的演化曲線Fig. 10 Evolution curves of steady state rheological rate under different upper limit of cyclic loading

3.2.3 加速流變階段損傷演化規律

圖11為不同黏性系數ηVP和損傷指數α條件下的黏塑性損傷元件流變曲線，由圖11可知，隨著ηVP值的減小，單位時間段內流變變形量增加，巖石的流變能力增強；與ηVP值不同，損傷指數α值越大，損傷發育越迅速，流變速率越大，加速流變曲線的非線性特征越明顯，說明損傷指數α值對加速流變階段的持續時間和流變曲線特征有明顯的控制作用。

圖11 ηVP和α對非線性黏塑性損傷元件流變曲線的影響Fig. 11 The effect of ηVP and α on rheological curves of nonlinear viscoplastic model

疲勞破壞階段巖石內部裂紋不斷擴展、交匯、貫通，損傷不斷累積，巖石塑性特征明顯。從圖11可以看出，循環荷載作用下巖石的流變曲線隨時間推移呈臺階狀增加，加載過程中，流變曲線的變形量顯著增加，卸載過程中，流變曲線增長較為平緩，循環荷載作用下巖石變形具有顯著的不可逆性[22]。由此可見，本文建立的黏塑性損傷元件不僅在整體變形規律方面與巖石疲勞破壞的加速流變特征相吻合，而且能很好地體現循環荷載作用下巖石不可逆黏塑性變形特征和損傷發育規律，具有明確的物理意義。

4 討論

本文通過建立循環荷載作用下巖石疲勞流變損傷模型，定量研究了不同上限荷載下粉砂巖的變形及損傷特性。在此基礎上，本節通過建立臨界損傷閾值判據和加速流變失穩破壞判據，開展巖石疲勞壽命預測分析，進一步明確本文所建立的循環荷載作用下巖石流變模型對巖體工程長期穩定性評價的意義。

4.1 加速流變損傷閾值及失穩判別準則

4.1.1 臨界損傷閾值判據

在巖石流變破壞過程中，發生加速流變時存在一個臨界損傷閾值，可以用裂紋臨界密度指標法、加速流變臨界應變法、全過程應力-應變曲線法、非彈性體積應變法等[23]方法判斷加速流變啟始的臨界條件。對于巖石疲勞變形及破壞特性，Brown和Hudson[24]、葛修潤[8]等發現巖石疲勞破壞時的軸向變形量與靜態應力-應變全過程曲線峰后區在循環載荷上限位置的變形量相當。如圖12所示，粉砂巖軸向平均應變的加速流變啟始點對應的應變閾值εa與循環荷載上限呈現良好的線性關系。因此，本文選擇疲勞流變損傷模型中黏塑性損傷元件應變閾值εa作為臨界損傷閾值判據。

圖12 臨界損傷閾值和加速流變啟始時間Fig. 12 Damage threshold and start time of accelerated creep

根據損傷閾值εa試驗值的擬合結果，給出循環荷載下粉砂巖加速流變啟始點的臨界損傷閾值判據：

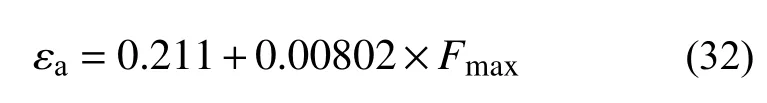
通過臨界損傷閾值判據獲取不同上限應力條件下損傷閾值εa的理論值，代入流變損傷式(25)可計算加速流變啟始時間ta的預測值。

4.1.2 加速流變失穩破壞判據

進入加速流變階段，流變模型中的黏塑性損傷元件啟動，軸向應變表現出顯著的不可逆性特征，流變曲線快速增長，損傷不斷累積。根據文中流變模型引入的損傷變量式(17)，當損傷變量D達到1時巖石發生加速流變失穩破壞，則可得加速流變失穩破壞判據為：

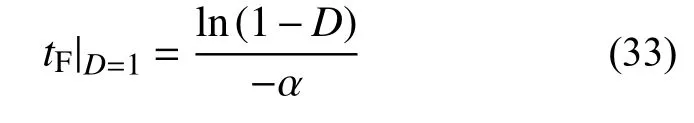
式中，tF為加速流變持續時間。

如圖13所示，對試驗結果進行擬合并獲取不同上限荷載條件下損傷指數α理論值，可通過加速流變失穩破壞判據式(33)計算獲取加速流變失穩破壞時間的預測值。

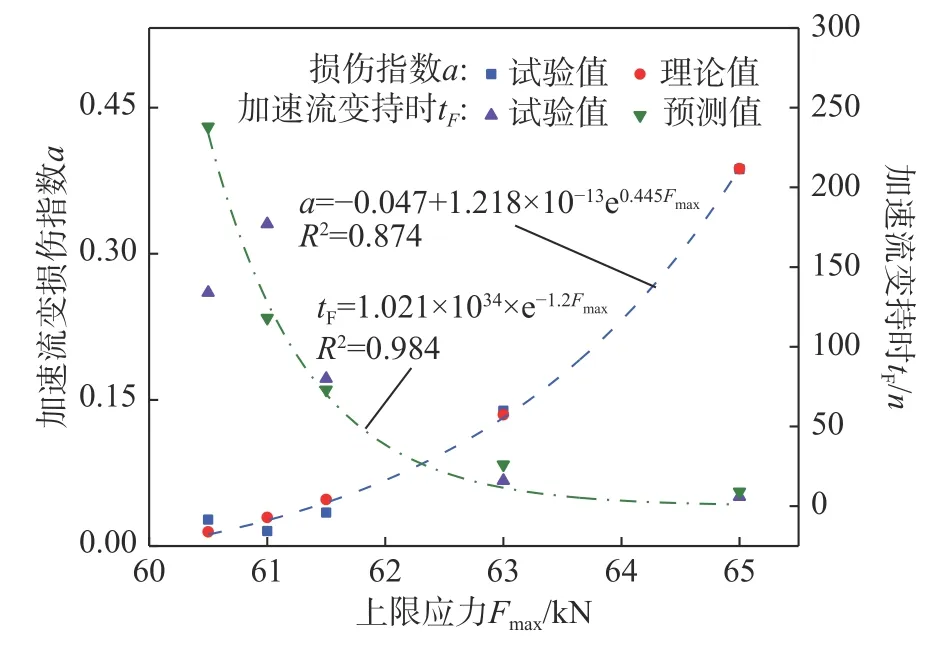
圖13 損傷指數和加速流變持續時間Fig. 13 Damage index and accelerated creep duration

4.2 巖石疲勞壽命預測

根據加速流變損傷閾值判據式(32)和加速流變失穩破壞判據式(33)可分別計算出進入加速流變階段所需循環時間和加速流變持續時間，因此可通過式(34)計算循環荷載作用下巖石的疲勞壽命預測值：

如圖14所示，上限荷載為60.5 kN、61 kN、61.5 kN、63和65 kN時，疲勞壽命預測值分別為1210次、869次、572次、118次和27次，疲勞壽命預測值與試驗值吻合度較高，并與上限荷載呈現良好的指數函數關系，說明采用本文建立的流變損傷模型對于定量研究循環荷載作用下巖石的疲勞特性及巖體工程長期穩定性評價具有一定的理論指導意義。

圖14 疲勞壽命預測結果Fig. 14 The results of fatigue life prediction

5 結論

本文以粉砂巖為研究對象，進行了不同上限荷載下巖石的疲勞變形破壞試驗，通過建立循環荷載作用下巖石的疲勞流變損傷模型，量化分析粉砂巖疲勞損傷流變全過程，得到以下結論：

(1) 開展了正弦波循環荷載作用下粉砂巖疲勞特性試驗，結果表明，巖石的變形表現出顯著的時間效應；上限荷載高于疲勞強度時，巖石發生疲勞破壞，流變曲線具有典型的初始變形、勻速變形和加速變形 3階段演化特征。

(2) 基于Kachanov流變損傷理論，將損傷變量引入一個帶有應力閾值和應變觸發的黏塑性元件，與Burgers模型串聯建立了巖石非線性疲勞損傷流變模型。與試驗相對應，將正弦波循環荷載應力函數替換流變微分本構方程中的恒定應力，推導了循環荷載下巖石一維、三維非線性流變損傷方程。

(3) 一維和三維狀態下理論值與試驗結果的吻合度較好，說明本文建立的非線性流變損傷模型不僅可以精確反映巖石的衰減流變和穩態流變，還可以準確地描述上限荷載高于疲勞強度時的加速流變階段。

(4) 定量分析循環荷載下流變全過程變形及損傷演化規律，結果表明，隨著上限荷載的增加，粉砂巖衰減流變和穩態流變階段的變形時效性顯著加強；加速流變階段損傷呈臺階狀累積發育，能很好體現循環荷載下巖石不可逆黏塑性變形特征。

(5) 提出了加速流變臨界損傷閾值判據和破壞失穩判據，并分別計算了加速流變啟始時間、加速流變持時理論值，疲勞壽命預測值與試驗值吻合度較好，新建流變模型對巖體工程長期穩定性評價具有一定的理論指導意義。