改進粒子群算法支持向量機的煙臺港貨物吞吐量預測

秦圻 周兆欣 韓洋 王士鵬 馬續仕

摘? 要：為了精準預測港口貨物吞吐量，文章研究了改進粒子群算法支持向量機模型。引入自適應慣性權重以及最優粒子擾動決策，來優化支持向量機中的懲罰參數C和核函數參數g。基于1978—2020年煙臺港吐吞量進行實證分析，對比改進支持向量機模型和原本支持向量機模型的平均相對誤差，預測效果優于SVM模型，因此為港口貨物吞吐量提供技術支持。

關鍵詞：核函數;支持向量機;改進粒子群算法;煙臺港

中圖分類號：TP18? ? ? ? 文獻標志碼：A文章編號：2096-4706（2022）03-0133-05

Cargo Throughput Prediction of Yantai Port Based on Improved Particle Warm Optimization Support Vector Machine

QIN Qi， ZHOU Zhaoxin， HAN Yang， WANG Shipeng， MA Xushi

（School of Navigation and Shipping， ShanDong JiaoTong University， Weihai? 264200， China）

Abstract： In order to accurately predict the cargo throughput of a port， this paper studies the improved Particle Swarm Optimization （PSO） support vector machine model. Adaptive Inertia Weight and optimal particle perturbation decision are introduced to optimize the penalty parameter C and kernel function parameter g in the support vector machine. This paper makes an empirical analysis based on Yantai Port throughput from 1978 to 2020， comparing the average relative error between the improved support vector machine model and the original support vector machine model， the forecasting effect is better than that of SVM model， therefore it provides the technical support for the port cargo throughput.

Keywords： kernel function; support vector machine; improved Particle Swarm Optimization; Yantai port

0? 引? 言

2021年，在全球疫情的影響下，港口作為對外貿易的重要樞紐，該如何面對困難，又該如何在疫情下突出重圍，如何在加快建設以國內大循環為主體、國內國際雙循環相互促進的新展格局上，扮演好港口作為樞紐的重要角色[1-3]？港口吞吐量決定了港口未來發展的方向，也對資源的配置起到了重要的作用，實施精準預測對港口建設和發展具有重要的意義[4]。目前，關于港口貨物吞吐量的預測方法有很多[5]，其中人工神經網絡在處理非線性方面的能力很高，但是容易陷入局部最優的困境[6，7]。支持向量機在小樣本非線性問題上有很強的解決問題的能力[8-10]。

目前，有很多學者通過優化或者改變支持向量機的參數來進行港口貨物吞吐量的預測，Du P等人提出了基于變分模式分解、機器學習、最優化算法和誤差修正策略的混合學習模型，用于集裝箱吞吐量預測[11]。Li L等人研究了非線性子序列的選擇性組合預測模型，對港口吞吐量進行預測[12]。陳錦文、蘭培真改進型BP神經網絡，將未來三年港口吞吐量作為輸出層參數，利用tansig函數和logsig函數為傳遞函數，對深圳港集裝箱吞吐量進行預測[13]。張雷雨、楊毅從影響集裝箱吞吐量的若干因素出發，基于主成分分析和支持向量機回歸算法的建模預測方法[14]。為了使支持向量機模型預測更加精準，劉路民根用網格搜索算法、遺傳算法、粒子群算法分別進行徑向基核參數尋優[15]。在港口貨物吞吐量預測方面用得最多是時間序列法[16]。其中，時間序列法主要有季節性變化法[17]、灰色系統法[18]、馬爾科夫法[19]、移動平均法[20]等。

煙臺港作為環渤海地區重要的港口，也是“一帶一路”倡議布局下的港口，對于它貨物吞吐量的研究較少。本文首先介紹了支持向量機的原理，懲罰參數和核函數參數的選擇影響著預測的精準性，因此，通過改進粒子群算法，來進行過參數的快速尋優，從而減少誤差，提高了改進支持向量機模型的擬合能力，為煙臺港在港口建設方面提供依據。

1? 支持向量機基本理論

支持向量機（Support Vector Machine， SVM）是由前蘇聯教授Vapnik最早提出的[21]。支持向量機是一種新型機器學習算法，其基本思想把原有數據訓練集映射到高維特征空間，借助損失函數和懲罰因子，從而達到精確度和計算復雜度相平衡[22]，因此，可以將上述問題看作一個在高緯度的二次回歸問題來進行求解，其函數表達式為：

f（x）=ω*φ（x）+b? ?（1）

其中，ω為超平面權重向量，根據文獻得到回歸支持向量機可以表示為：

（2）

（3）

其中，是松弛變量C，是正實數松弛懲罰因子。

非線性回歸求解中，可以使用核函數K（xi，xj）=φ（xi）φ（xj）把所需要的訓練集映射到高維空間，從而就可以將其變化到線性問題的擬合，可得到一樣的效果，非線性擬合函數為：

（4）

則將問題轉化為對偶求解：

（5）

其中，ηi，，ai，為拉格朗日乘子，b為閾值。

2? 改進粒子群算法

2.1? 自適應慣性權重

PSO算法由于需要調整的參數較少，因此魯棒性高且更容易實現[23]。但是，粒子群算法的缺點就是尋優過程中出現收斂速度慢和陷入局部最優的問題，為了避免算法進入局部最優，可以從一開始粒子群進化速度和聚集度的變化，引入自適應慣性權重來調整其運動狀態，表達式為：

（6）

ω=exp（-λ（k）/λ（k-1）） （7）

其中，k為迭代數，λ（k），為衡量慣性權重變化的平滑度，ω為慣性權重fgbest（PSi（k）為第i個粒子在第k次更新位置的時候對應的個體極值適應度值，fzbest（PSi（k））為第k迭代更新位置時候最優粒子對應的極值適應度值。

2.2? 最優粒子擾動決策

粒子群算法在迭代過程中，隨著次數的增加粒子之間呈現聚集的趨勢從而降低了搜索的能力，容易跳入局部最優。粒子群算法的全局最優位置fgbest（t）在整個粒子群的尋優過程中具有較強的引導作用[24，25]。為了避免此問題的出現，需要在粒子群聚集過程中，改變全局最優的位置來進行干擾，從而增大粒子的活動范圍，因此最優粒子的決策表達式為：

（8）

ri=|xi-avg_x| （9）

（10）

其中，avg_x（j）為粒子群所屬粒子的中心位置第j緯，i為第i個粒子，r（i）為第i個粒子與粒子群中心位置的距離。式（10）為全部粒子到中心位置的平均距離。

若avg_r變大則表示粒子群比較分散，也就是說明粒子群還具有很強的多樣性，此時只需要輕微的擾動全局最優位置，就可以增強粒子群的局部搜索能力。反之，則需要對全局最優位置進行更大的干擾，使得粒子增加搜索范圍。

3? 改進粒子群算法支持向量機模型

支持向量機中的懲罰參數C是模型對誤差的容忍度，數值越大，容忍度越差;數值越低，欠擬合越容易。其次就是核函數參數g的選取對支持向量機的學習能力和預測精度有很大的影響。在使用支持向量機對數據進行訓練時，為了使模型準確度達到一定的要求，需要不斷地調整C和g的值，并對數據不斷地進行交叉驗證，以找到合適的C和g的值。

本文則使用改進的粒子群算法來快速尋優到最佳懲罰參數和核函數參數，為解決粒子群算法收斂慢及陷入局部最優的，通過引入自適應權重和最優粒子決策達到搜索平衡，以參數作為初始位置的粒子群一步一步走向全局最優，在最優位置fgbest（t）處迅速收斂。本模型中改進的粒子群算法主要搜索優化支持向量機中的懲罰參數C和核函數參g，在得到懲罰參數C和核函數參數g的最優值的基礎上對煙臺港貨物吞吐量進行預測。

基本步驟：

第1步：根據初始化過程，將參數設置為粒子配置隨機位置和速度。

第2步：為了使得粒子群能過擴大搜索區域，對其設置最優粒子干擾決策。

第3步：通過自適應權重及最優擾動，計算每個粒子的適應度值。

第4步：以參數作為粒子進行尋優，將所選取的適應值與當前粒子經歷的最佳位置的適應值進行比較，如果適應值更好，則將其更新到當前最佳位置。

第5步：對于粒子群中的粒子，將當前粒子的適應值與所有全局粒子所經歷的最佳位置的適合值進行比較，如果更好，則更新為當前全局最佳位置。

第6步：對于每個粒子的速度和位置按照一定規律進行優化。

第7步：當適應度值滿足設置的最大迭代次數在結束條件允許下，反之需要返回第2步。

4? 煙臺港貨物吞吐量實證分析

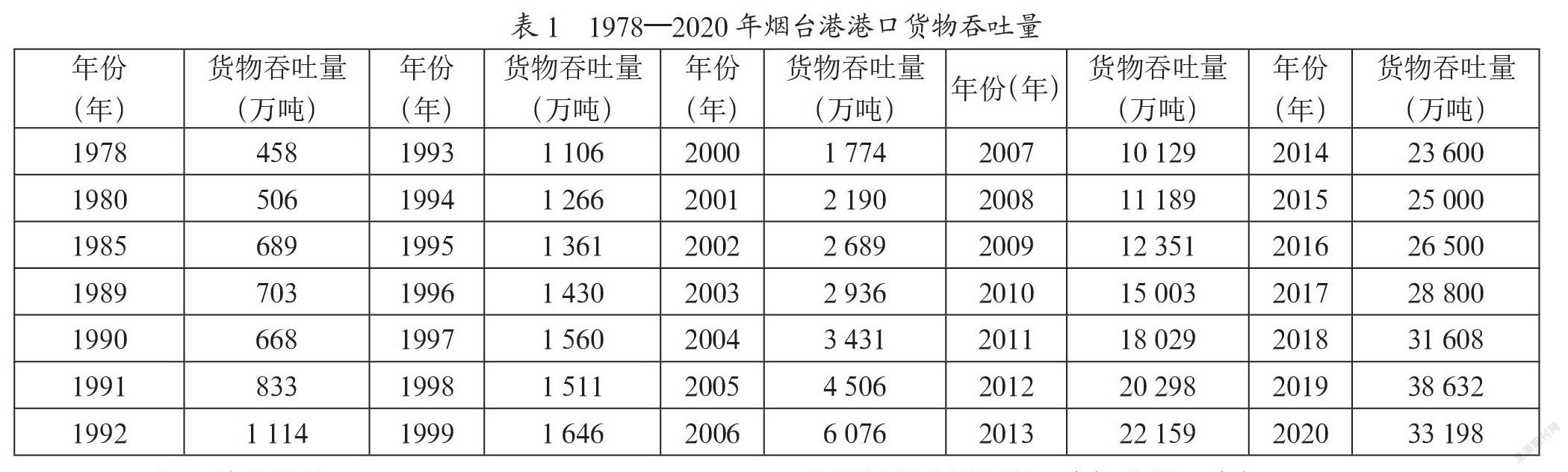
本文以煙臺港貨物吞吐量為研究對象選取了1978—2020年的數據進行模型驗證數據來源國家統計年鑒如表1所示，其中以1978—2016的煙臺港貨物吞吐量為模型的訓練數據，2017—2020年的吞吐量作為預測數據。本文才有對比的方法進行試驗，一種采用基本的支持向量機模型，另外一種就是改進粒子群算法優化支持向量機模型。在進行預測模型訓練之前，則需要對原本的數據歸一化處理，將其大小限制在[0，1]之間，公式為：

（11）

其中，xj表示第j個樣本煙臺港貨物量的歸一化值，xmin，xmax，表示煙臺港貨物量存在的最小值和最大值。

4.1? 優化模型訓練

根據改進支持向量機模型，通過MATLAB 2016進行算法編寫。改進支持向量機預測模型時將粒子群算法全局搜索能力設置為2，種群個數為40，最大迭代次數500，慣性因子設置為0.8，在適應度函數方面選取Griewank函數。最后，基于改進粒子群算法優化支持向量的參數經過迭代，得到SVM的最優參數C=217 226.657 238和g=1.683 678 926，如圖1所示。

4.2? SVM預測

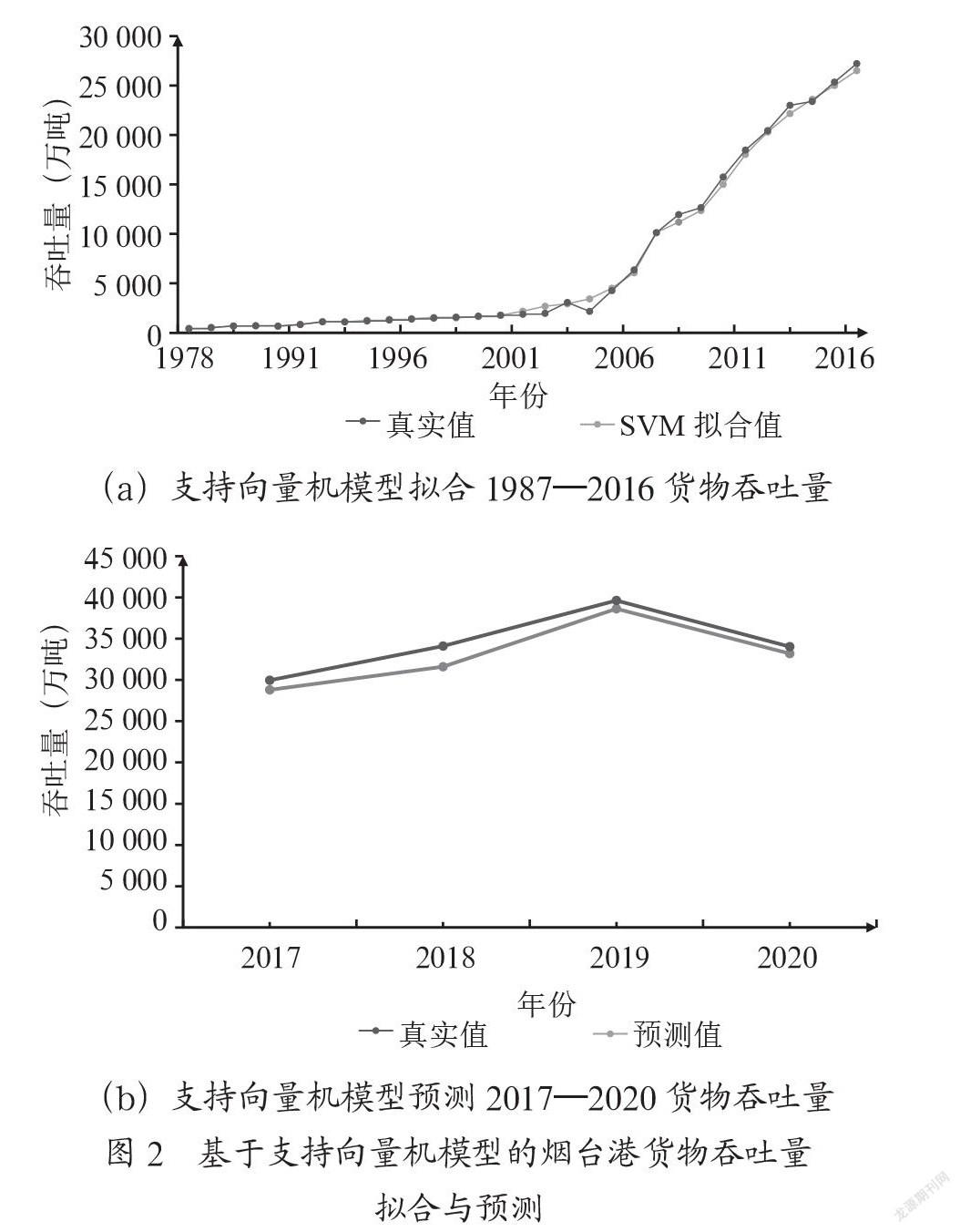
從圖2（a）可看出，通過基本的支持向量機模型對煙臺港貨物吞吐量數據擬合時，由于需要人為設定SVM的參數，從而導致了擬合訓練數據時出現了幅度較大的偏差，用設定的參數進行預測的時候，從圖2（b）可以看出，預測的曲線與真實值有相當大的差別，預測效果較差。

通過改進粒子群算法，加入了自適應權重，使系統魯棒性更高，再利用最優粒子擾動決策，來防止過擬合現象發生。以煙臺港1978年—2016年貨物吞吐量作為訓練集。在預測時將粒子群算法全局搜索能力設置為2，種群個數為40，種群個數、最大迭代次數與參數取值的上下界保持一致，其中自適應度函數是將訓練樣本的擬合均方差與測試樣本的預測均方差之和作為判別標準。經過改進支持向量機模型的擬合與測試圖分別為圖3（a）和圖3（b）。

4.3? 結果評價

通過相對誤差進行改進支持向量機的有效性評價，也能體現其預測的精準度，表達式為：

（12）

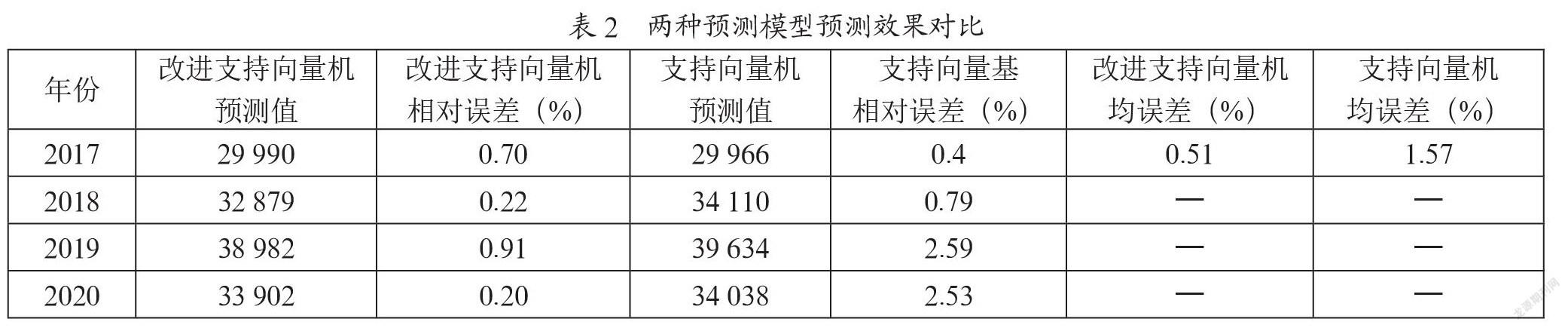
如表2所示，對2017—2020年的煙臺港貨物吞吐量預測所產生的相對誤差分別為0.7%、0.22%、0.91%、0.2%，結果與實際的結果很接近，其次相對誤差都遠小于基礎支持向量機預測模型。因此表明改進支持向量機預測模型擁有較高的預測精度，為港口準確預測貨物吞吐量提供理論依據和參考。

5? 結? 論

本文在對自適應權重以及最優粒子擾動決策來改進粒子群算法容易跳入局部最優的問題，用其對支持向量機的參數進行優化，選取1978年—2016年煙臺港貨物吞吐量數據進行模型的擬合和預測。為了檢驗此模型預測的精準度引入相對誤差來進行評價，同時將改進的支持向量機模型與支持向量機模型進行對比，來證明經過改進的模型更加合理準確。實例表明，在改進粒子群優化算法支持向量機的預測的相對均誤差為0.51%，要遠遠小于原本支持向量機模型的平均相對誤差，預測效果優于SVM模型。該研究僅僅采用了改進粒子群算法對支持向量機的參數進行尋優，并沒有將其他算法優化結果與之對比，在以后的研究中將會進一步完善。

參考文獻：

[1] 賈大山，徐迪，蔡鵬.2020年沿海港口發展回顧與2021年展望 [J].中國港口，2021（S1）：1-13.

[2] 李慧.基于Holt-Winters算法的長江干線貨物吞吐量分析及預測 [J].中國水運，2021（4）：29-32.

[3] 李香暉.通道建設“提速”港口吞吐“增量” [N].欽州日報，2021-11-01（2）.

[4] 孔琳琳，劉瀾，許文秀，等.基于時間序列分析的港口集裝箱吞吐量預測分析 [J].森林工程，2016，32（5）：106-110.

[5] DELURGOIO S A. Forecasting Principles and Applications [M].Boston：Irwin/McGraw-Hill，1998.

[6] 占祖桂.基于BP神經網絡的香港離岸人民幣匯率預測 [J].吉林金融研究，2018（8）：44-46.

[7] 馬廣慧，馬豆豆，邵秀麗.基于遺傳BP神經網絡的三七價格預測 [J].天津師范大學學報（自然科學版），2017，37（6）：76-80.

[8] DONG B，CAO C，LEE S E. Applying support vector machines to predict building energy consumption in tropical region [J].Energy and Buildings，2005，37（5）：545-553.

[9] 居錦武.基于LS-SVM的養殖水體氨氮含量分析模型的優化 [J].大連海洋大學學報，2016，31（4）：444-448.

[10] 趙合勝.基于灰色預測和SVM的茶葉烘焙溫濕度預測 [J].西安文理學院學報（自然科學版），2018，21（5）：64-67

[11] DU P，WANG J Z，YANG W D，etal. Container throughput forecasting using a novel hybrid learning method with error correction strategy [J/OL].Knowledge-Based Systems，2019，182：[2021-12-02]. https：//www.sciencedirect.com/science/article/abs/pii/S0950705119303284.

[12] MO L L，XIE L，JIANG X Y.et al. GMDH-based hybrid model for container throughput forecasting：Selective combination forecasting in nonlinear subseries [J].Applied Soft Computing，2018，62：478-490.

[13] 陳錦文，蘭培真.改進型BP神經網絡的港口吞吐量預測 [J].集美大學學報（自然科學版），2019，24（5）：352-357.

[14] 張雷雨，楊毅.基于PCA-SVM的港口集裝箱吞吐量預測模型研究 [J].江蘇商論，2019（5）：33-38.

[15] 劉路民根.支持向量機徑向基核參數優化研究 [J].科學技術創新，2018（26）：48-49.

[16] 余國剛，馮琪，徐粉.張家港永嘉集裝箱碼頭集裝箱吞吐量組合預測 [J].物流技術，2017，36（4）：103-107.

[17] 杜剛，劉婭楠.季節性變動影響下的上海港集裝箱吞吐量預測 [J].華東師范大學學報（自然科學版），2015（1）：234-239.

[18] 張緒進，母德偉，韓濤.改進的灰色預測模型在過壩貨運量預測中的應用 [J].水運工程，2009（6）：4-7.

[19] 王慧，吳茜茜.空間自回歸模型中系數變量及誤差項的貝葉斯估計 [J].合肥工業大學學報（自然科學版），2021，44（9）：1291-1296

[20] LIM S，KIM S J. PARK YOUNGJAE，et al. A deep learning-based time series model with missing value handling techniques to predict various types of liquid cargo traffic [J/OL].Expert Systems With Applications，2021，184：[2021-12-02]. https：//www.sciencedirect.com/science/article/pii/S0957417421009404.

[21] 陳旭，李典，張利華，等.基于改進支持向量機（SVM）模型的荊州港吞吐量預測 [J].水運工程，2020（3）：38-42.

[22] SCH?LKOPF B，SMOLA A J. Learning with Kernels：Support Vector Machines，Regularization，Optimization and Beyond [M].[S.I.]：The MIT Press，2001.

[23] 馬秋芳.改進PSO優化的BP神經網絡短時交通流預測 [J].計算機仿真，2019，36（4）：94-98+323.

[24] 林權，何正東，倉偉，等.一種基于復合儲能的自適應權重粒子群算法研究 [J].機電信息，2021（28）：8-9+13.

[25] YAN L，WANG H，WANG H，et al. An improved OS-ELM based Real-time prognostic method towards singularity perturbation phenomenon [J/OL].Measurement，2021，182：[2021-12-02].https：//www.sciencedirect.com/science/article/abs/pii/S0263224121006424？via%3Dihub.

作者簡介：秦圻（1996—），男，漢族，江蘇如皋人，碩士研究生在讀，研究方向：航運科學與技術。