基于字典序乘積下廣義和連通度指標的上下界

李志豪， 朱 焱

（ 華東理工大學數學學院，上海 200237）

拓撲指標是與圖的化學結構相關聯的一種數學方法，分子圖的拓撲指標值不僅可以定量地表達分子的結構，也能用來分析分子的結構與活性之間的關系，并且這些拓撲指標值在圖的自同構下是不變的，所以它已成功地與有機分子的物理和化學性質相關聯，因此對于拓撲指標的研究至關重要。但研究難點在于有些化合物分子比較復雜，拓撲指標的計算量比較大。

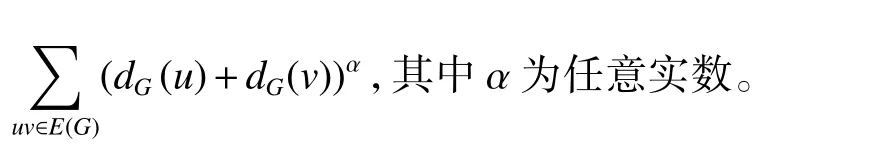
Onagh[6]研究了關于字典序乘積圖的F-和的調和指標。Akhter 等[7]研究了關于笛卡爾乘積圖的F-和的廣義和連通度指標。Du等[8]研究了當非零實數大于或等于?1時，具有n個頂點的單圈圖的廣義和連通度指標的最小值和次最小值，并且確定了相對應的極圖。Tomescua 等[9]確定了不同樹的廣義和連通度指標的最小值。

本文把基于笛卡爾乘積下運算圖的廣義和連通度指標上下界推廣到基于字典序乘積下運算圖的廣義和連通度指標的上下界，然后計算了基于字典序乘積下運算圖的廣義和連通度指標的上下界，并對于每一個定理都分別給出了一個運算圖的例子，計算了其廣義和連通度指標，同時與定理中的上下界進行比較，從而驗證了定理。

1 基本概念

令G是一個有限、簡單、連通的無向圖，其點集和邊集分別為V=V(G) ，E=E(G) 。對于任意頂點v∈V，dG(v)表示v的度。Pn表示有n個頂點的路。對于給定的連通圖G，4種相關圖[10]定義如下：

(1) 在圖G的每條邊上嵌入一個新的頂點，將新頂點與所對應邊的兩個端點連接，這樣圖G中的每條邊就變成了長為2的路，由此得到的圖記為S(G) 。

(2) 在圖G的每條邊外，都加一個與之相對應的新的頂點，然后再把每個新的頂點與其相對應邊的兩個端點連接，由此得到的圖記為R(G) 。

(3) 在圖G的每條邊上嵌入一個新頂點，將新頂點與所對應邊的兩個端點連接，然后再把圖G中相鄰兩條邊所對應的新頂點連接起來，由此得到的圖記為Q(G) 。

(4) 在圖G的每條邊外，都加一個與之相對應的新的頂點，再把每個新的頂點與其相對應邊的兩個端點連接，然后再把圖G中相鄰兩條邊所對應的新的頂點連接起來，由此得到的圖記為T(G) 。

如果G為P6，則S(P6) ，R(P6) ，Q(P6) 和T(P6)分別如圖1所示。

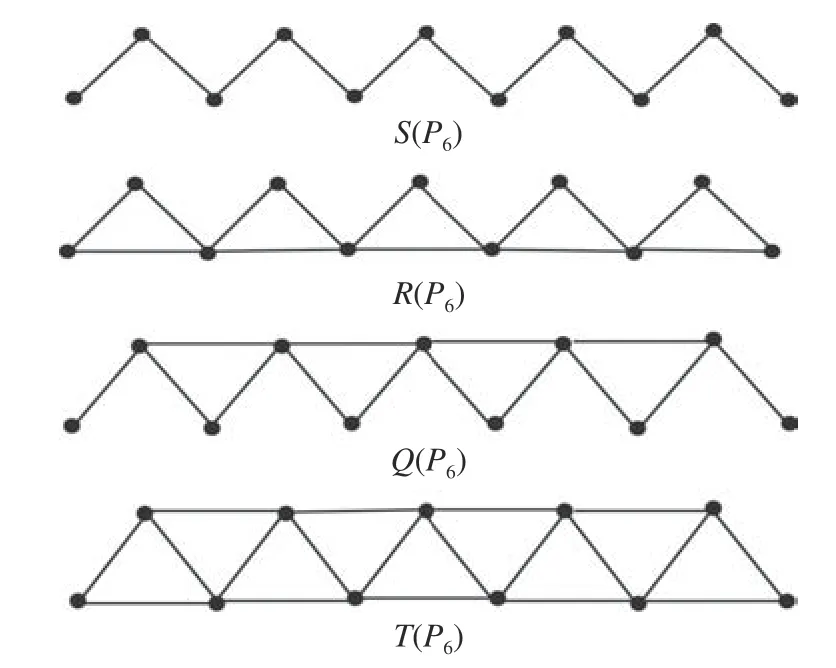
圖1 F∈{S,R,Q,T} 時F(P6)的4種運算Fig. 1Fouroperations ofF(P6)atF∈{S,R,Q,T}

兩個連通圖G0和G1的字典序乘積G0[G1] 定義為：其點集為V(G0)×V(G1) ，其圖中的兩個點 (a1,b1)和 (a2,b2) 相鄰當且僅當a1與a2在G0中相鄰或者b1與b2在G1中相鄰且a1=a2[11]。

Sarala等[12]在兩個連通圖G0和G1的字典序乘積的基礎上介紹了圖的4種新運算。

令F∈{S,R,Q,T} ，則G0和G1關于字典序乘積的F-和G0[G1]F定義為F(G0)[G1]?E?，其中E?={(a,b1)(a,b2)∈E(F(G0)[G1]):a∈V(F(G0))?V(G0)，b1b2∈E(G1)}。

若G0=G1=P3，則P3[P3]S，P3[P3]Q，P3[P3]R，P3[P3]T如圖2所示。

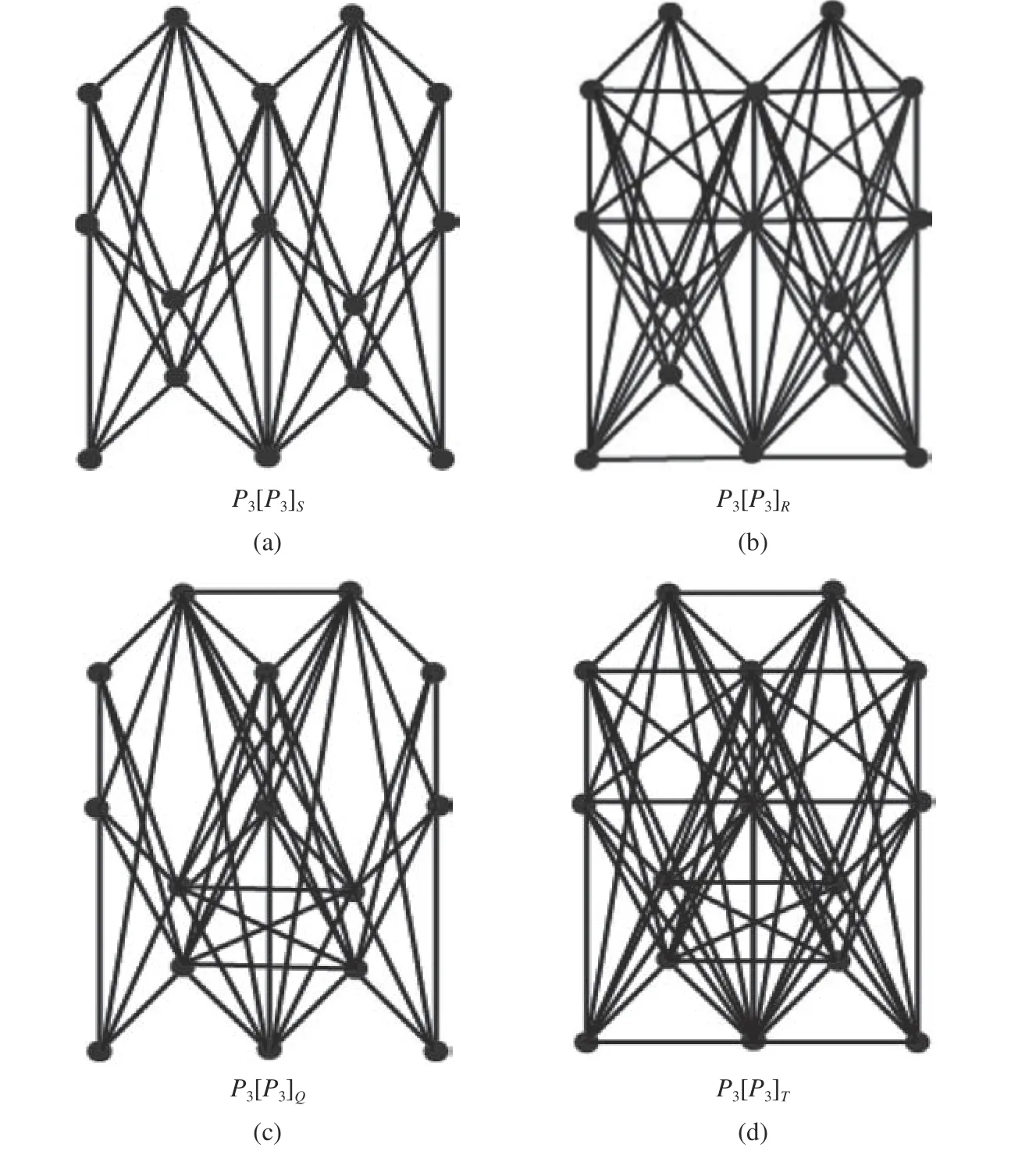
圖2 F∈{S,R,Q,T} 時圖P3[P3]的4種運算Fig. 2 Four operations on graph P3[P3] at F ? {S,R,Q,T}

2 主要結果

本文確定了關于字典序乘積圖的F-和的廣義和連通度指標的上下界。令n1,m1分別表示圖G0的頂點數和邊數，n2,m2分別表示G1的頂點數和邊數， δG0和 ?G0分別表示圖G0的最小度和最大度， δG1和 ?G1分別表示圖G1的最小度和最大度。本文首先考慮F=S。

定理1當 α 為負數，廣義和連通度指標滿足不等式γ1(S)≤χα(G0[G1]S)≤γ2(S)，其中，

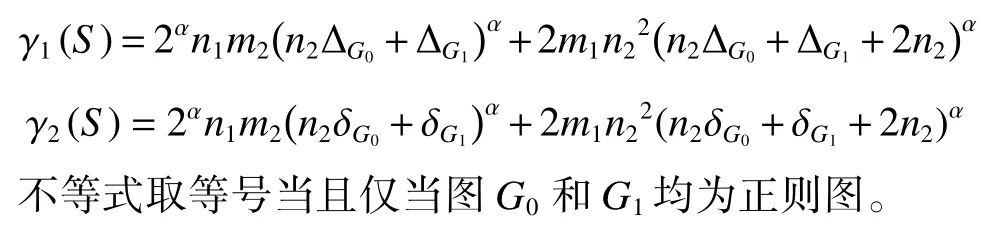
證明：

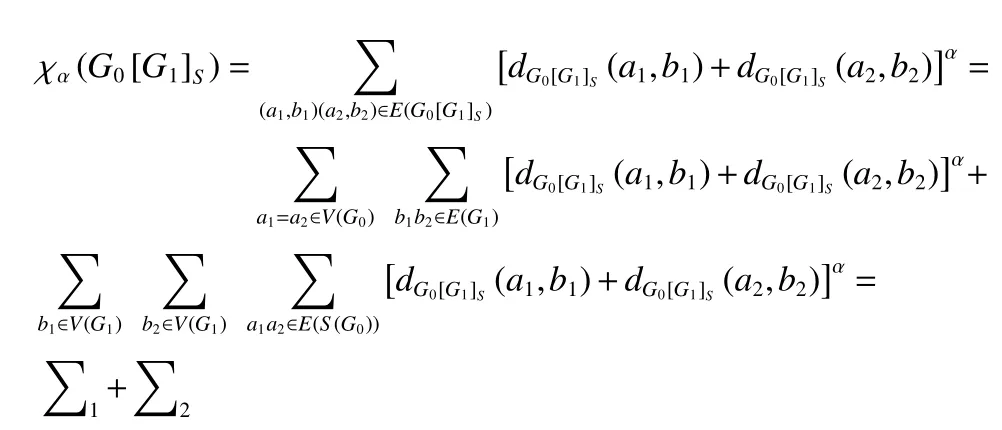
由于對于a1∈V(G0) ，有dS(G0)(a1)=dG0(a1) ，所以式（1）成立。

由等式 |E(S(G0))|=2|E(G0)|=2m1，當a2∈V(S(G0))?V(G0) 時，dS(G0)(a2)=2 ，所以

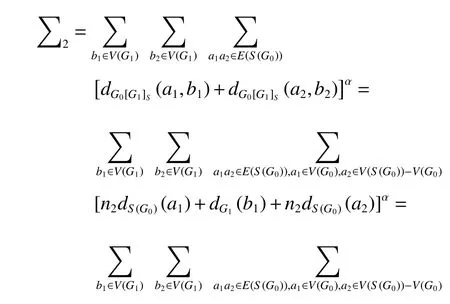
[n2dG0(a1)+dG1(b1)+2n2]α≥2m1n22(n2?G0+?G1+2n2)α

同理可得

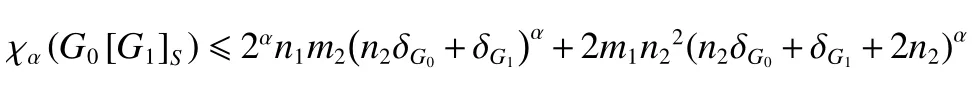
不等式取等號當且僅當圖G0和G1均為正則圖。

為了驗證定理1的上下界，本文舉例1說明。

例1：當G0=P4,G1=P2時，

χα(G0[G1]S)=2×6α+2×10α+8×7α+16×9α

γ1(S)=4×10α+24×9α

γ2(S)=4×6α+24×7α

滿足 γ1(S)≤χα(G0[G1]S)≤γ2(S) 。

定理2當F=R時，對于負數 α ，廣義和連通度指標滿足不等式 γ1(R)≤χα(G0[G1]R)≤γ2(R) ，其中

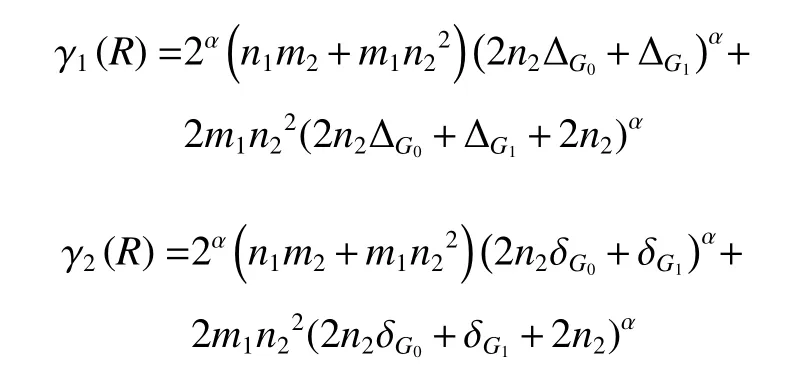
不等式取等號當且僅當圖G0和G1均為正則圖。

證明：

由于 δG0≤dG0(a)≤?G0,δG1≤dG1(b)≤?G1，不等式取等號當且僅當圖G0和G1均為正則圖，因此可以得到

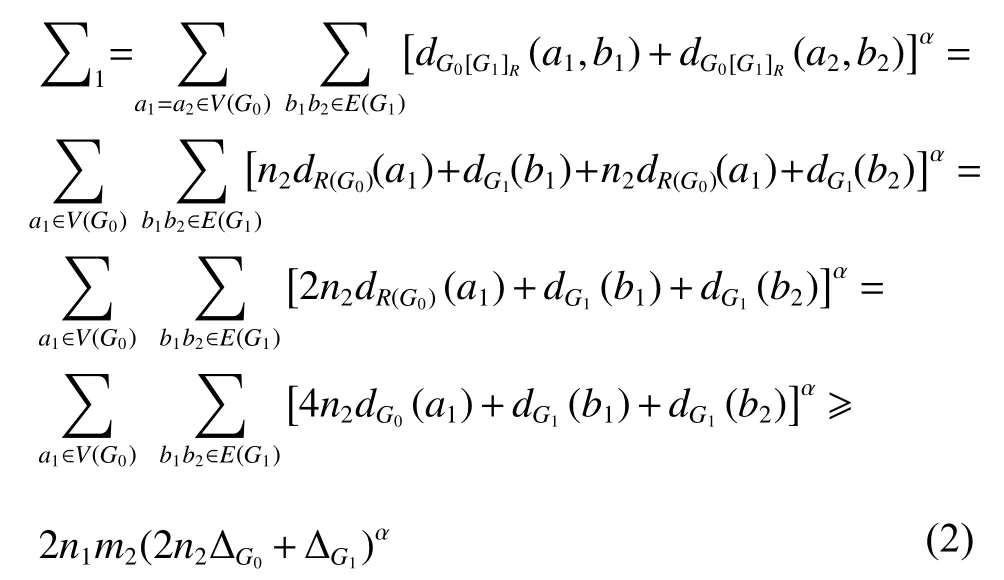
由于對于a1∈V(G0) ，有dR(G0)(a1)=2dG0(a1) ，所以式（2）成立。

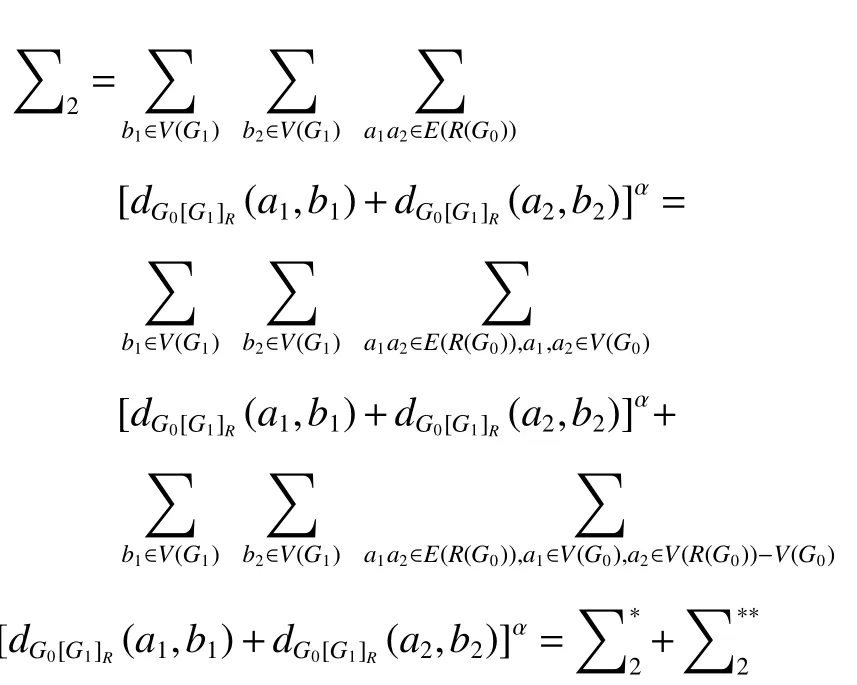
由于dR(G0)(a1)=2dG0(a1) 、a1a2∈E(R(G0)) 和a1,a2∈V(G0) 當且僅當a1a2∈E(G0) ，因此

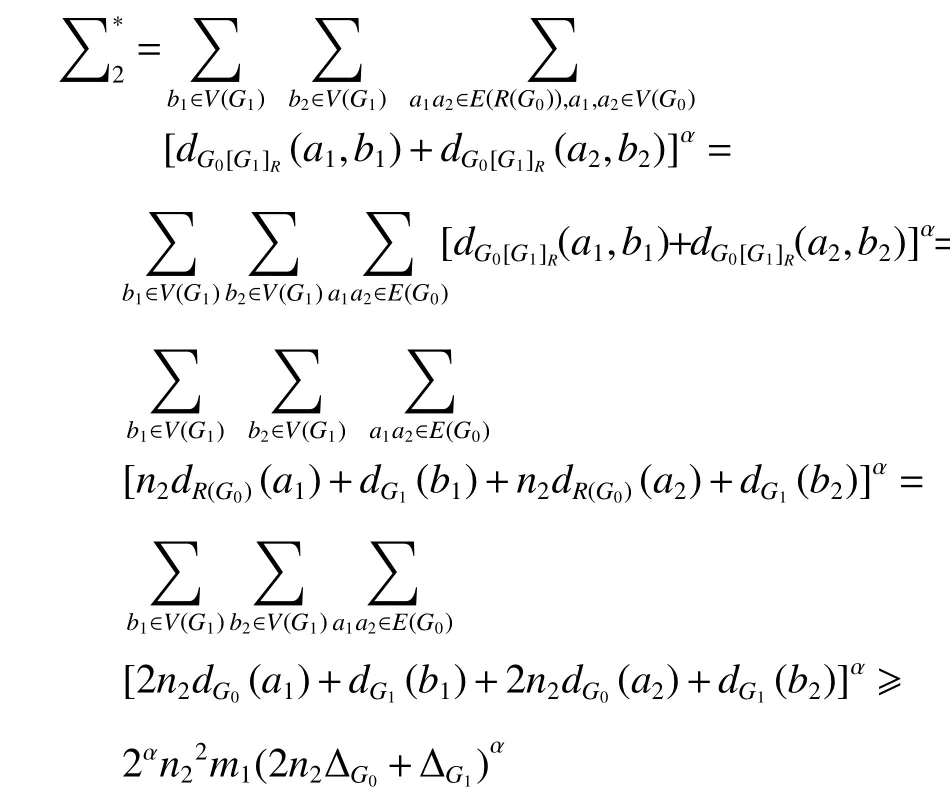
由等式 |E(R(G0))?E(G0)|=2|E(G0)|=2m1，當a1∈V(G0) 時，dR(G0)(a1)=2dG0(a1) ；當a2∈V(R(G0))?V(G0)時，dR(G0)(a2)=2 ，所以

不等式取等號當且僅當圖G0和G1均為正則圖。

為了驗證定理2的上下界，本文舉例2說明。

例2：當G=P4,H=P2時，

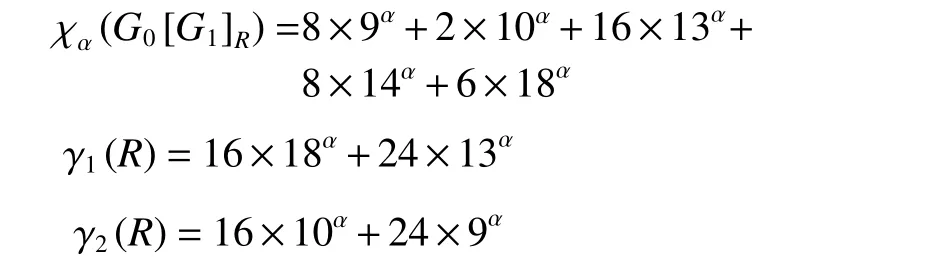
滿足 γ1(R)≤χα(G0[G1]R)≤γ2(R) 。

定理3當F=Q時，對于負數α，廣義和連通度指標滿足不等式γ1(Q)≤χα(G0[G1]Q)≤γ2(Q)，其中

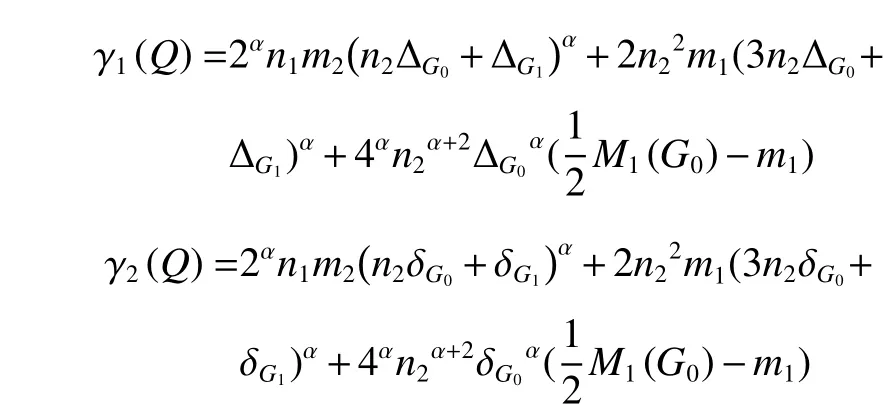
不等式取等號當且僅當圖G0和G1均為正則圖。

證明：

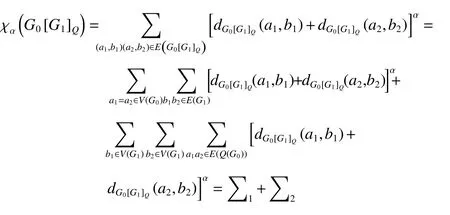
由于 δG0≤dG0(a)≤?G0,δG1≤dG1(b)≤?G1，不等式取等號當且僅當圖G0和G1均為正則圖，因此可得

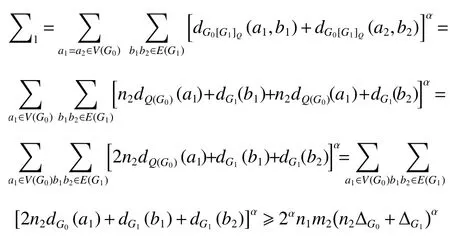
由于對于a1∈V(G0) ，有dQ(G0)(a1)=dG0(a1) ，所以式（3）成立。

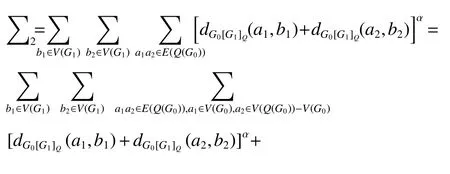
由于a1和a2分別對應于G0中的邊wiwj和wjwk，因此

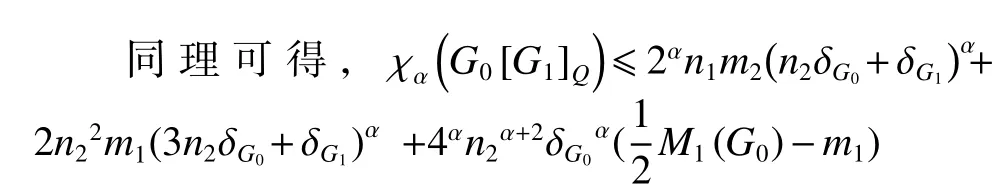
不等式取等號當且僅當圖G0和G1均為正則圖。

為了驗證定理3的上下界，本文舉例3說明。

例3： 當G=P4,H=P2時，

定理4當F=T時，對于負數 α ，廣義和連通度指標滿足不等式 γ1(T)≤χα(G0[G1]T)≤γ2(T) ，其中

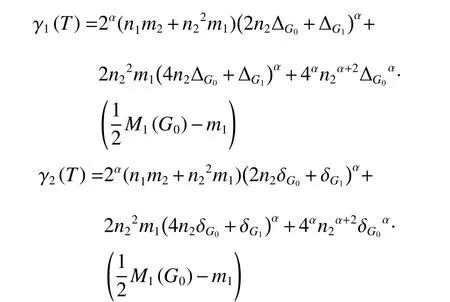
不等式取等號當且僅當圖G0和G1均為正則圖。

為了驗證定理4的上下界，本文舉例4說明。

例4： 當G=P4,H=P2時，

χα(G0[G1]T)=2×10α+8×11α+16×14α+8×15α+8×17α+6×18α

γ1(T)=16×18α+8×16α+24×17α

γ2(T)=8×8α+24×9α+16×10α

滿足 γ1(T)≤χα(G0[G1]T)≤γ2(T) 。

3 結 論

本文先給出了基于字典序乘積的4種運算，并得到運算圖中頂點的度與未做運算的圖的度之間的關系，再利用最大度和最小度計算了在 α＜0 的情況下基于字典序乘積的圖的4種運算下的廣義和連通度指標上下界，即 γ1(F)≤χα(G0[G1]F)≤γ2(F) ，其中F∈{S,R,Q,T}。如果α，>0那么γ2(F)≤χα(G0[G1]F)≤γ1(F)。因此對于其他的不同乘積，也可以把這4種運算推廣到其他乘積上面，同樣找出乘積圖中頂點的度與圖G0、G1中頂點的度之間的數量關系，再利用最大度最小度求出廣義和連通度指標的上下界。不過困難的是對于有些乘積，很難找出乘積圖中頂點的度與原圖中頂點的度之間的關系。