基于誤差修正NLSTM 神經網絡的無人機航跡預測

梁天宇, 高 永, 劉軍民, 惠永昌

(1. 西安交通大學數學與統計學院，西安 710049; 2. 海軍航空大學航空基礎學院，煙臺 264001)

0 引言

無人機全稱“無人駕駛飛行器”，英文縮寫為“UAV”(Unmanned Aerial Vehicle)，是利用無線電遙控設備和自備的程序控制裝置操縱的不載人飛機[1]。它被廣泛應用于軍用和民用等領域。隨著無人機產業的蓬勃發展，無人機航跡預測也成為當前世界研究的熱點。例如，對無人機進行快速準確的航跡預測可以提高作戰效率，進行任務規劃和及時提供沖突解決方案；通過航跡預測可以建立有效的無人機監管系統，保障民航航班的運行安全等。

目前，國內外對于飛行器航跡預測的方法主要包括兩類：空氣動力學方法和無參數估計方法。空氣動力學模型在航跡預測的應用中普遍存在參數過多、預測精度較低等問題[2]。無參數估計方法因不考慮飛行器動力學參數從而簡化模型，被廣泛研究并應用于航跡預測。

無參數估計方法可分為傳統的統計學算法和當前發展迅猛的神經網絡算法。統計學方法主要是利用數理統計的方法處理歷史數據，對歷史數據進行曲線擬合以及參數估計，不斷提高預測精度，包括回歸預測法、蒙特卡羅法、卡爾曼濾波算法等。例如，Wu 和Pan[3]提出一種基于數據挖掘的飛行軌跡預測模型，采用二元線性回歸法預測下一次的飛行時間，從大量歷史位置數據分析飛機每個時間點的位置；Lymperopoulos 和Lygeros[4]證明了序列蒙特卡羅法在多飛行器航跡預測中的有效性；Prevost 等[5]采用改進的卡爾曼濾波(Improved Kalman Filter, IKF)算法估計無人機追蹤的運動目標的狀態，并通過計算預測誤差來評價預測軌跡的質量；羅兆文等[6]建立了基于滑窗多項式最小二乘擬合的航跡預測法，對于短期預測有較好的效果。

在基于神經網絡的航跡預測方面，徐婷婷等[7]設計了三層反向傳播(Back Propagation, BP)神經網絡模型用于船舶的航跡實時預測，其結果體現了神經網絡較強的非線性逼近能力與魯棒性。楊彬和賀正洪[8]利用廣義回歸神經網絡(Generalized Regression Neural Network, GRNN)對高超聲速飛行器進行軌跡預測。吳一凡和冉曉旻[9]將卷積神經網絡(Convolutional Neural Networks, CNN)引入到航跡預測中，并且證明了其在小樣本航跡預測中具有較高的準確性。

以上應用于航跡預測的算法各有優點，但是僅把航跡數據看出空間中的獨立數據點，沒有充分利用其軌跡時序上的相關性。循環神經網絡(Recurrent Neural Networks,RNN)是一種具有代表性的神經網絡模型，其結構非常適用于處理時間、空間上有強關聯的動態序列數據。然而，傳統的RNN 由于其結構過于簡單，對序列數據的記憶能力會逐漸下降，不能存儲長期記憶，即無法解決長期依賴問題。為克服這一問題，Hochreiter 和Schmidhuber[10]提出了長短期記憶神經網絡(Long Short-Term Memory, LSTM)。它改進了原RNN 中的記憶單元，以不同的方式計算隱層神經元的狀態，從而使得神經網絡具有更長時間的記憶能力。目前，LSTM 已被廣泛應用于各個領域的預測研究中。

鑒于此，本文首次提出利用RNN 以及其變體LSTM 對無人機飛行軌跡進行預測，傳統的LSTM 用于預測時仍存在精度不夠高等問題。針對傳統LSTM 模型的不足，本文提出一種帶誤差修正的嵌套長短期記憶網絡(Error-corrected Nested LSTMs, ENLSTM)航跡預測模型。該模型能夠通過對歷史數據的訓練實現對無人機的航跡預測，并且利用誤差模型對網絡進行修正，得到更準確的預測航跡。在無人機的模擬飛行數據和真實行訓練數據上的仿真對比實驗表明所提出的ENLSTM 模型能更加有效地預測無人機的飛行軌跡，證實模型的可行性。

1 相關理論

1.1 RNN 循環神經網絡

循環神經網絡(RNN)是一類專門用于處理序列數據的神經網絡，比如時間序列、文本語句、語音等。RNN 不僅考慮前一個時刻輸入的影響，并且考慮以前時刻輸入的影響，所以賦予了網絡“記憶”的功能。RNN 的向前傳播中折疊了一個循環計算的重復結構，即對于一個序列，其當前狀態ht包含了過去所有狀態ht?1對其的影響，以及當前時刻外部輸入xt的影響，即

一個最簡單的RNN 架構如圖1 所示，左邊是循環未展開的部分，右邊是展開的結構。RNN 主要由輸入層、隱藏層和輸出層組成，隱藏層的箭頭表示數據的循環更新，即實現網絡的記憶功能。其中x表示輸入的樣本，o表示輸出的預測，W表示隱藏層從前一時刻轉移到后一時刻的權重矩陣，U表示輸入層到隱藏層的權重矩陣，V表示隱藏層到輸出層的權重矩陣，網絡中每個單元共享一組(W,U,V)，實現參數共享可極大地降低計算量。

圖1 RNN 網絡結構圖

根據圖1 的網絡結構，RNN 的前向傳播過程如下：

1) 時刻t的隱狀態

2) 時刻t預測輸出

其中f、g均為激活函數，用于篩選重要信息。f可以采用tanh、relu 和sigmoid 函數等，g通常取為softmax 函數；

3) 對于離散分類任務，該網絡的損失函數一般為交叉熵，而對于連續預測任務，損失函數通常是均方誤差，即

通過將每個時刻的輸出值的誤差反向傳播和梯度下降法，可以對RNN 的權重參數進行更新，在不斷調整參數的過程中提高模型性能。

1.2 NLSTM 嵌套長短期記憶網絡

隨著時間序列變長，RNN 的反向傳播過程中可能會出現梯度消失和梯度爆炸的問題，這導致其難以傳遞相隔較遠的信息。因此，RNN 的一系列變種算法被提出，其中最具有代表性的是LSTM。如果說RNN 能夠使得網絡擁有短暫的“記憶”，那么LSTM 則是擴展了網絡的“記憶”，能夠解決長期依賴問題。LSTM 在RNN 的基礎上加了三個門來控制，網絡結構為圖2。

如圖2 所示，LSTM 神經網絡也如同RNN 分為輸入層、隱藏層和輸出層，隱藏層中增加了三個門結構，分別是遺忘門、輸入門和輸出門。

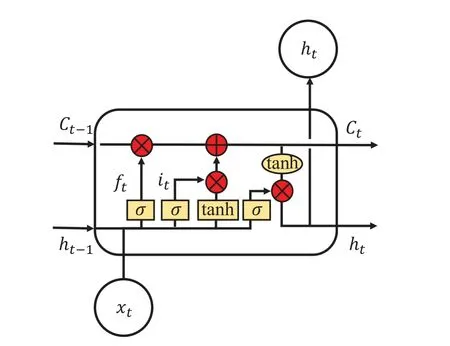
圖2 LSTM 網絡結構圖

1) 遺忘門決定保留多少上一層的細胞ct?1中的舊記憶信息，流入當前時刻的xt與上一時刻傳遞過來的狀態ht?1，通過對應的所有事件步共享的權重Wxf、Whf，偏移bf進行線性組合，并通過sigmoid 函數進行處理后得到對舊記憶信息的保留比例ft，即

2) 輸入門控制了有多少新記憶信息可以流入，即生成新記憶信息和新記憶信息的使用比例it，接著融合舊信息與新信息生成新的記憶細胞ct，對應下式

其中⊙表示矩陣的元素相乘，tanh 為激活函數。

3) 基于新的記憶細胞ct以及輸出門計算的比例值ot，得到最終的輸出ht

關于LSTM 模型的變體有很多，為了提高模型的精度，增加LSTM 網絡的深度是一種較為常用的方法。嵌套長短期記憶網絡(Nested LSTMs, NLSTM)[11]，則是通過加入一個狀態函數，從而有選擇性地訪問內部記憶信息，使得網絡能夠處理更長時間規模的序列，網絡結構如圖3 所示。其中狀態函數mt用于替換LSTM 網絡中ct計算式(7)中的加和，即在NLSTM 中

圖3 Nested LSTMs 網絡結構圖

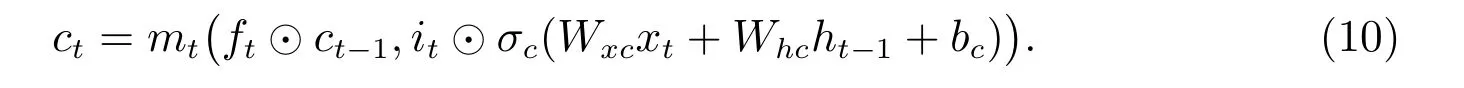
如果將mt作為一個LSTM 記憶單元，則NLSTM 中記憶函數的輸入和隱藏狀態為

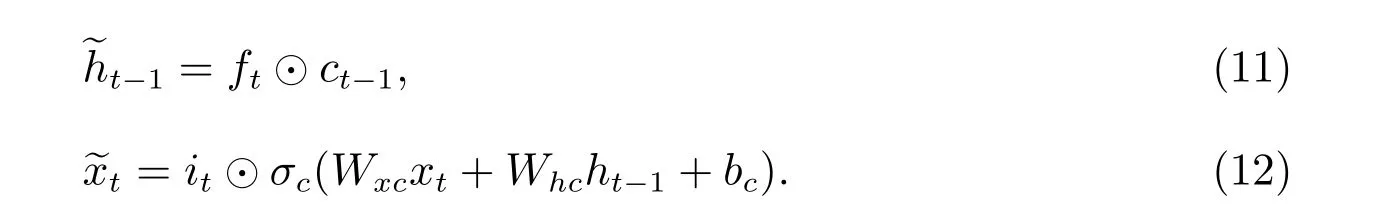
那么NLSTM 的內部計算過程如下

NLSTM 的外部記憶信息為

通過嵌套長短期記憶網絡的架構可以看出，它創造了一種記憶的時間層級，通過門控的方式去訪問內部記憶，以便于選擇性地去訪問長期記憶信息。同時增加了網絡的深度，有效提高模型的性能。

2 帶誤差修正的NLSTM 網絡預測無人機航跡模型

2.1 誤差修正

影響無人機飛行軌跡預測產生誤差的因素有很多，首先良好的預測模型需要高精度的數據作為支撐，而由于數據采集與監控系統采集的數據可能存在誤差以及采樣頻率不穩定等原因造成產生異常數據是影響預測精度的重要原因[12]。其次，模型自身存在局限性。進行軌跡預測需要建立數學模型，即將實際問題進行抽象、化簡，模型只能在理論上以一定的精度逼近實際問題而無法真實地刻畫[13]。例如由于網絡訓練精度限制以及參數設置，誤差不可避免地存在。最后，預測時長和樣本容量大小的選取也會對預測精度產生影響。例如，隨著預測序列長度的增加以及新的預測數據的影響，誤差會逐步累積。

為了進一步縮小預測誤差以提高預測結果的可信度，需要進行誤差修正。早期的誤差修正技術出現在對測量儀器的校正上，隨著計算機的飛速發展，誤差修正在技術實現上有了飛躍的進步，程序化、自動化和環境自適應修正得以實現。信號處理技術的發展更是充實和完善了誤差修正的建模技術。在誤差建模方面，其基本算法包括解算方法、仿真方法和一些輔助方法等，近年來還出現了一些計算機集成算法工具，如Matlab 工具箱，為誤差建模的實施提供很大的幫助[14]。

本文為了提高預測精度，提出誤差修正策略。在建立NLSTM 預測模型后，利用誤差建模技術對預測軌跡進行校正，建立誤差模型

2.2 算法模型

本文基于深度學習框架Tensorflow 建立NLSTM 網絡，各部分結構與參數設置如下：

1) 隱藏層結構與參數：考慮到輸入樣本的數量較少，本文將隱藏層層數設為1，即建立一個單層的NLSTM 網絡，神經元個數為20，添加無激活函數的全連接層，嵌套深度設置為2；

2) 模型訓練參數：模型在訓練前需要指定損失函數和優化器。本文選擇均方誤差作為損失函數和Adagrad 優化器不斷更新參數，進行預測模型的優化。設置訓練批尺寸為50，訓練輪數為1 000；

3) 預測評價指標：為了便于預測值與真實值比較，分析模型的預測效果，選擇均方根誤差作為評價指標

結合2.1 的誤差修正，本文提出的ENLSTM 預測模型整體框架為圖4。

圖4 ENLSTM 預測模型框架

3 實驗及結果分析

為了驗證本文提出的ENLSTM 網絡模型對無人機航跡預測的可行性和普適性，實驗部分對模擬飛行數據和無人機實際飛行數據分別進行預測，根據軌跡預測圖及預測誤差進行分析。

3.1 數據描述

1) 模擬飛行數據采用四種含有隨機噪聲的三維曲線，使用70%的數據點作為網絡的訓練集，剩下30%作為測試集。參數方程式及取值范圍如表1 所示。

表1 模擬數據的參數方程式及取值范圍

2) 實驗使用的無人機訓練飛行的真實數據是通過Mission Planner 加載航線日志，導出mat 格式的飛行數據再利用Matlab 軟件加載數據。接著從GPS 標簽中選擇經度、緯度和高度三個航跡指標作為網絡的輸入進行無人機的航跡預測。由于該無人機的四邊航線飛行訓練過程中，分為上升、平飛和下滑三個階段，其中平飛階段為27 圈，采樣點數量為9 477，本實驗使用平飛階段前26 圈的經度、緯度和高度三個航跡指標數據作為模型的訓練集，剩下的數據用于測試。

3.2 數據預處理

數據的預處理包括數據歸一化和構造時間序列樣本集兩部分。

1) 數據歸一化

由于輸入變量的量綱不同，為了消除其影響，本文選擇對輸入的樣本數據，即經緯度和高度進行z-score 標準化處理，以提高預測的準確性，公式如下

2) 構造時間序列樣本集

設定時間步長為T，用前T個樣本點的歷史數據預測下一時刻的數值，即采用時刻t ?T到時刻t ?1 的數據作為預測的輸入序列，時刻t的數據作為預測的輸出，以此生成連貫的時間序列類型樣本集。

3.3 模型參數分析

為了得到誤差相對較小的最優模型，首先進行ENLSTM 預測模型部分超參數的分析與優化。根據經驗以及樣本長度，分別選擇20、30、40、50 作為預測的時間步長和0.12、0.1、0.08 作為Adagrad 優化器的學習率訓練模型，并且計算測試數據的預測值與真實值的均方根誤差RMSE。表2 為使用ENLSTM 模型對無人機真實飛行軌跡進行預測的誤差。

表2 不同時間步長和學習率下預測模型的RMSE

根據表2，選出均方根誤差最小的模型參數，即預測時間步長設為50，優化器的學習率為0.1，此時RMSE 為0.109 2。

3.4 對比試驗

為了驗證ENLSTM 模型預測效果的優越性，本文使用BP 神經網絡、單層RNN 和單層LSTM 分別對模擬數據和對實際飛行數據進行預測，對比效果。對于BP 神經網絡，本文設計一個三層的BP 神經網絡，輸入長度為50 個時刻的位置坐標，隱藏層的節點數為20 個，輸出為下一時刻的位置坐標。設置隱藏層的傳遞函數為對數S 型函數，輸出層的傳遞函數則為線性函數；訓練方法采用Levenberg-Marquardt 算法；學習率設為0.1；訓練次數設為1 000。單層RNN 和單層LSTM 模型的參數設置和ENLSTM 類似。

四個模型對于模擬飛行數據的預測曲線為圖5 至圖8，對于真實飛行數據的預測曲線為圖9，其中黑色實線為真實航跡，藍色星號線為ENLSTM 的預測軌跡，虛線為LSTM、RNN 和BP 三種模型的預測結果。可以較為直觀地看出，ENLSTM 模型的預測軌跡更接近于真實軌跡。

圖5 模擬數據1 的預測曲線與真實曲線

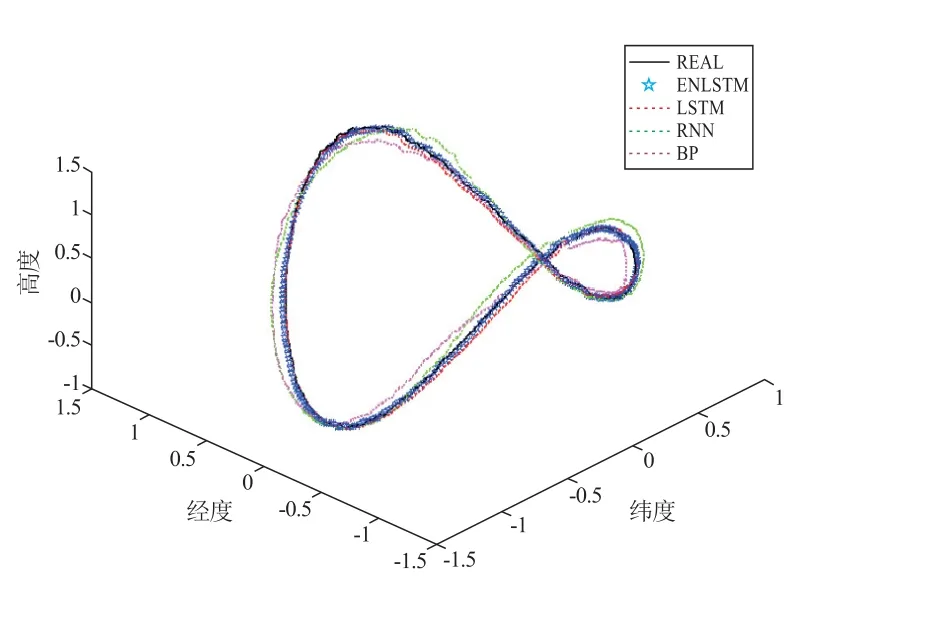
圖6 模擬數據2 的預測曲線與真實曲線

圖7 模擬數據3 的預測曲線與真實曲線

圖8 模擬數據4 的預測曲線與真實曲線

圖9 真實數據的預測軌跡與真實軌跡

通過計算，四種模型預測結果的RMSE 為表3。針對模擬數據，ENLSTM 模型的預測序列與真實序列的誤差RMSE 分別為0.086 1、0.021 1、0.025 5 和0.087 1，實際飛行數據的預測誤差RMSE 為0.109 2，比起LSTM、RNN 和BP 模型的預測結果，誤差都有了顯著減小，說明本文提出的模型在預測性能方面有了明顯的改進。并且從四種模型的預測誤差依次遞減，可以說明循環神經網絡相對BP 神經網絡在時間序列數據的預測上更具有優勢，以及基于基礎循環神經網絡的逐步改進提升了模型的預測能力。

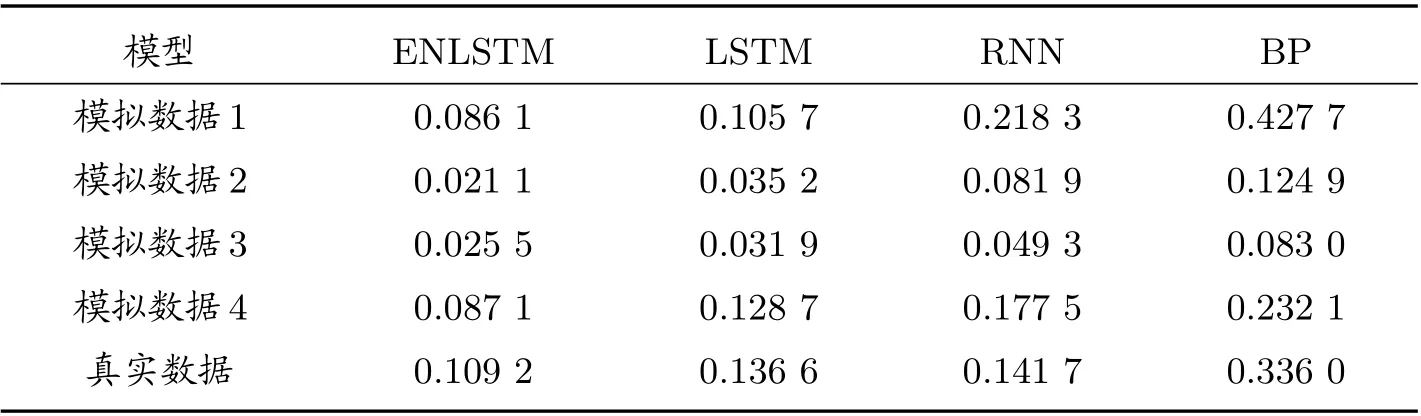
表3 四種模型預測結果的RMSE

4 總結與展望

本文將NLSTM 神經網絡應用到無人機的航跡預測中，并且通過誤差建模對預測值進行修正。將提出的ENLSTM 預測模型分別應用到無人機的模擬飛行軌跡和真實飛行軌跡，通過不斷優化參數，可以使模型達到較好的預測效果。同時與BP、RNN、LSTM 神經網絡對比，實驗表明在參數基本相同的情況下，ENLSTM 模型預測精度更高。針對無人機的航跡預測問題，ENLSTM 模型有著較好的應用效果。同時ENLSTM 仍存在權重參數較多使得訓練時間較長的問題，下一步將對ENLSTM 模型的網絡結構進行優化，使得預測結果準確且高效。