基于遺傳算法和復合二次徑向基函數的復合材料層合板自由振動分析

李 琳, 石 峰, 項 松, 趙為平, 王艷冰

(1. 沈陽開放大學數字化資源制作管理服務中心，沈陽 110003;2. 沈陽航空航天大學遼寧省通用航空重點實驗室，沈陽 110136)

0 引言

復合材料層合板具有較高的比強度，已經被廣泛應用于航空、航天、建筑、船舶等領域。很多學者研究了復合材料層合板的自由振動問題，Khdeir 和Reddy[1]用二階剪切變形理論分析了復合材料層合板的自由振動問題，Roque 等[2]用三角分層理論和徑向基函數分析了復合材料層合板和夾芯板的振動問題，Ferreira 等[3]利用一階剪切變形理論和徑向基函數分析了對稱復合材料層合板的自由振動問題，Aagaah 等[4]用三階剪切變形理論計算了復合材料層合板的固有頻率，Akhras 和Li[5]用樣條有限條和高階剪切理論計算了復合材料板的靜力和振動問題，Baharlou 和Leissa[6]計算了任意邊界條件復合材料層合板的振動和屈曲，Shi 等[7]計算了任意完全固支復合材料層合板的振動問題，Liew 等[8]利用一階剪切變形理論和無網格法分析了復合材料板的自由振動和屈曲，項松和石宏[9]用逆復合二次徑向基函數分析了復合材料層合板的自由振動問題，Xiang 等[10]用薄板樣條徑向基函數分析了固支復合材料層合板的自由振動問題，Xiang 等[11]利用無網格局部徑向基配點法分析了復合材料層合板的自由振動問題，Xiang 等[12]利用n階剪切變形理論分析了復合材料層合板的自由振動問題。

在無網格徑向基配點法分析過程中，針對所分析問題的不同，徑向基函數的形狀參數對計算精度有很大影響。文獻[9—12]中的徑向基函數都是用固定的形狀參數，導致了計算精度不高。

遺傳算法是一種隨機搜索算法，是一種利用復制、交叉和變異等遺傳操作來模擬自然進化，完成問題尋優的現代優化方法[13]。

本文將遺傳算法引入到復合材料層合板的自由振動問題中，利用遺傳算法對復合二次徑向基函數的形狀參數進行了優化，用優化了形狀參數的復合二次徑向基函數計算了復合材料層合板的固有頻率，將計算結果與文獻中的結果進行了對比。對比結果表明：本文方法具有較高的計算精度。

1 控制方程和邊界條件

僅由0?鋪層和90?鋪層交替依次疊合、壓制而成的層合板，稱為對稱正交鋪設層合板，見圖1。

圖1 對稱正交鋪設層合板

對稱正交鋪設層合板的位移場如下

式(1)中，w、?x、?y是中面的位移分量，h是層合板的厚度。

應變分量如下

x ?y ?z坐標系下的應力應變關系為

式(4)中

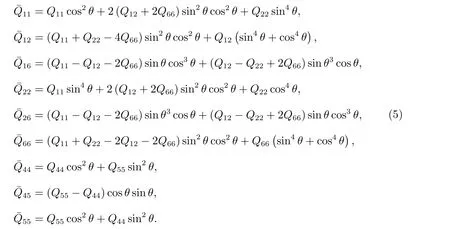
式(5)中，θ是纖維方向和x軸的夾角

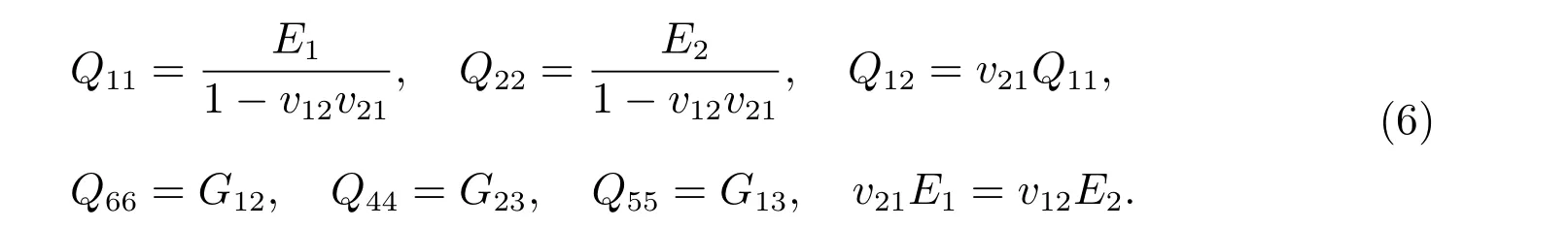
利用虛功原理可以獲得如下的歐拉-拉格朗日方程

式(7)中

式(7)～(9)中，α和β代表x和y，Ii是慣性分量

式(10)中ρ代表材料密度。

將式(8)和式(9)帶入式(7)，可以得到如下方程

n是總層數，zk和zk+1第k層的下面和上面的z坐標

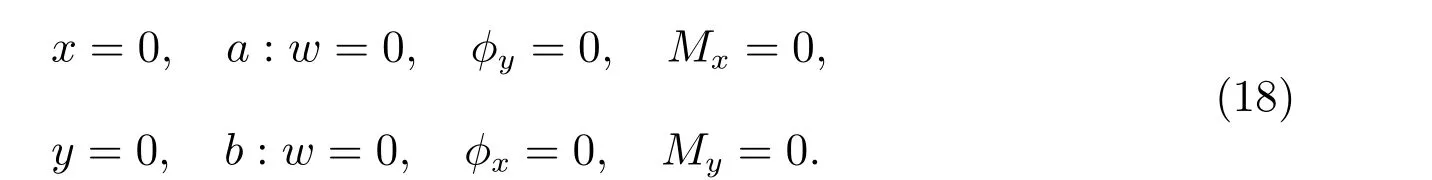
假設w、?x、?y為

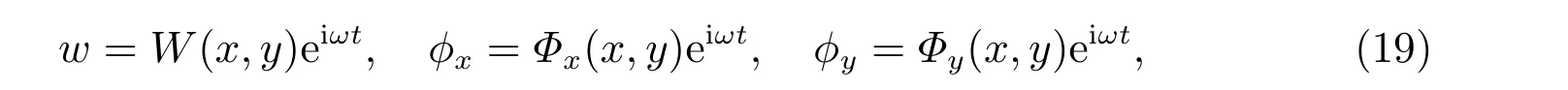
式(19)中，ω是自由振動的固有頻率。將式(19)帶入式(11)～式(13)可以獲得如下方程

2 無網格方法

無網格徑向基配點法不需要網格及節點之間的連接關系，將結構離散成一系列節點，使用問題域中的全部節點對偏微分方程的解進行近似，具有耗時少、計算精度高等優點。

根據無網格徑向基配點法，W、Φx、Φy可以用如下函數近似

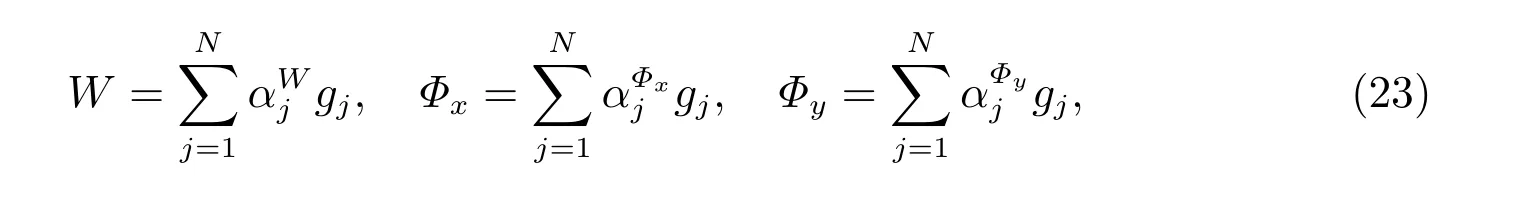
將式(23)帶入簡支邊界條件，可以對邊界條件進行離散，將離散的邊界條件和控制方程寫成如下形式

3 遺傳算法

遺傳算法是近年來涌現的一種現代優化方法，這種算法采用的是“生成+檢驗”優化模式，它的基本操作包括編碼、產生初始種群、計算適應度、判斷目標函數是否滿足優化條件。如果滿足優化條件，迭代結束；如果目標函數不滿足優化條件，就經過遺傳、交叉、變異操作產生下一代種群，然后返回重新每個個體計算適應度，依次循環。具體步驟如下：

步驟1 隨機產生一定規模的初始種群，對每個個體計算適應度；

步驟2 按照一定的法則對種群進行選擇，通常采用輪盤賭的方法對種群進行選擇；

步驟3 然后對選擇下來的種群進行一定概率的兩兩交叉產生新種群；

步驟4 新的種群中的個體按一定概率發生變異；

步驟5 判斷是否滿足優化條件，滿足則結束，不滿足則轉到步驟2。

遺傳算法框圖如圖2 所示。

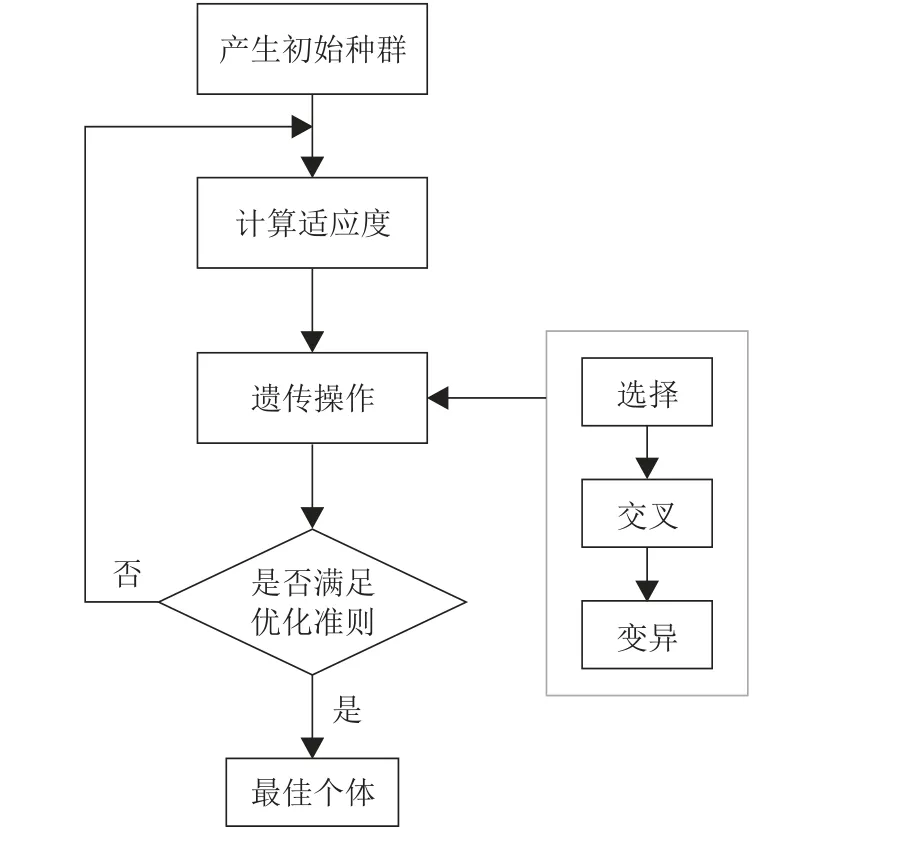
圖2 遺傳算法框圖

在遺傳算法中，目標函數的選取對遺傳算法的影響很大，它是用遺傳算法對參數進行尋優的指標。而對目標函數值的使用是通過評價個體的適應度來體現的。

徑向基函數的形狀參數對計算精度有很大影響，本文采用遺傳算法對復合二次徑向基函數的形狀參數進行優化，可以獲得最優的形狀參數，以提高計算精度。

4 數值算例

復合材料層合板每層的材料屬性如下

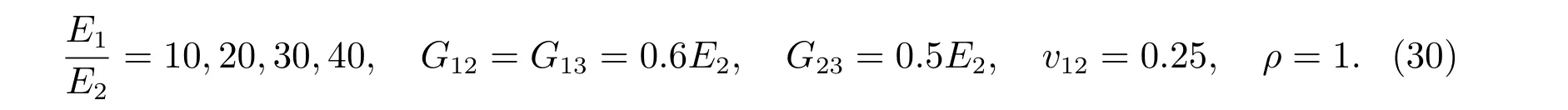
圖3 為復合材料方板規則的節點離散方式，本文中采用的節點數為15×15，固有頻率按下式進行無量綱處理

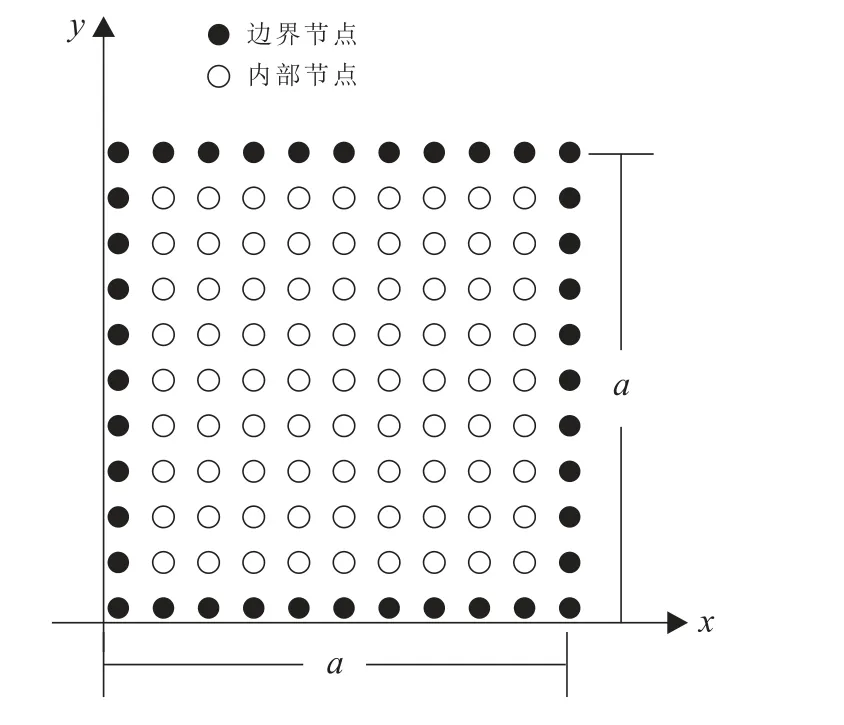
圖3 方板的規則節點離散

本文優化的參數是αc，取值范圍[0.5,?5]；選擇簡支方板(0?/90?/0?, E1/E2 =40, a/h= 2,5,10,100)的無量綱基頻的計算結果與文獻[14]中結果的差值的和最小作為目標函數。

樣本個數越大，越可能找到全局解，但運行時間也相對較長，一般在40～100 之間取值，本文使用的樣本個數為50，遺傳操作時交叉概率pc=0.8，變異概率pm=0.2。采用二進制編碼，經過100 代尋優。

在上述條件下最后得到優化的參數值為αc= 1.920 8，用優化了形狀參數的復合二次徑向基函數計算了復合材料層合板的固有頻率，將計算結果與文獻中的結果進行了對比，如表1 至表3 所示。

表1 列出了簡支方板(0?/90?/0?, E1/E2 = 40)的無量綱基頻，從表1 可以看出本文結果與文獻[14]的結果的一致性較好。

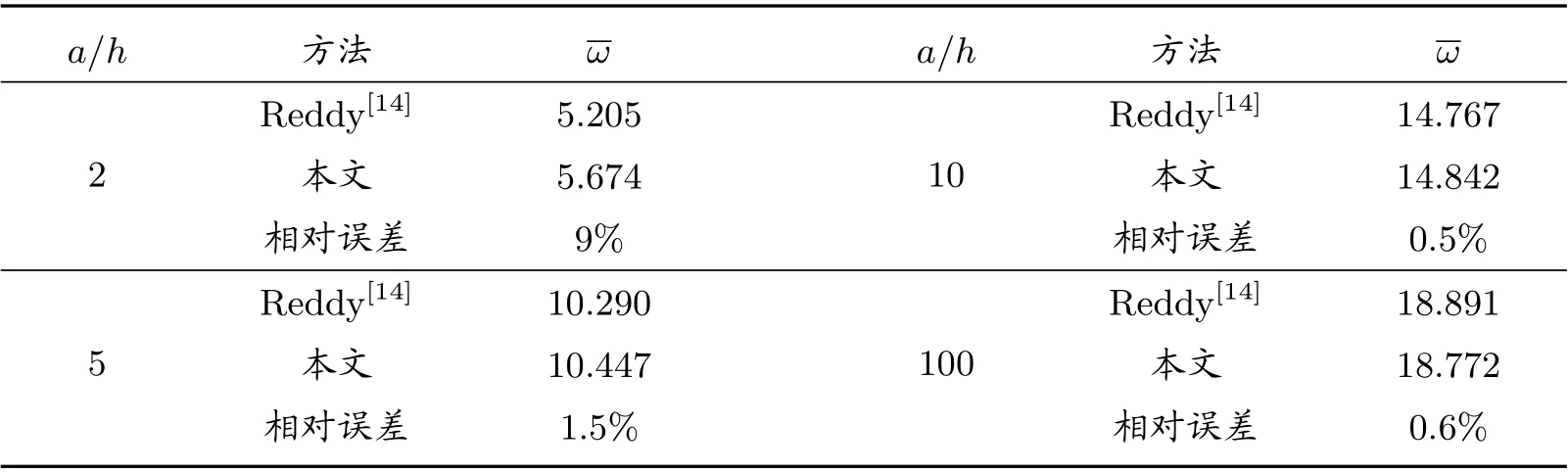
表1 簡支方板的無量綱基頻(0?/90?/0?, E1/E2 =40)

表2 列出了簡支方板(0?/90?/90?/0?, E1/E2 = 40)的無量綱基頻，從表2 可以看出本文結果與文獻[15]的結果具有較好的一致性。

表2 簡支方板的無量綱基頻(0?/90?/90?/0?, E1/E2 =40)

表3 列出了簡支方板(0?/90?/0?, E1/E2 = 40, a/h= 10)的無量綱前三階固有頻率，從表3 可以看出本文結果與文獻[16]的結果具有較好的一致性。

表3 簡支方板的無量綱前三階固有頻率(0?/90?/0?, E1/E2 =40, a/h=10)

5 結論

本文采用無網格徑向基配點法分析了復合材料層合板的自由振動問題，利用遺傳算法對復合二次徑向基函數的形狀參數進行了優化，最后得到優化的參數值為1.920 8。用優化了形狀參數的復合二次徑向基函數計算了復合材料層合板的固有頻率，將計算結果與文獻中的結果進行了對比。對比結果表明：遺傳算法在形狀參數優化方面具有很大的潛力，本文方法具有較高的計算精度。