基于遺傳算法的五模材料分層優化?
孫雪聰 孫兆永 賈 晗 畢亞峰 楊 軍
(1 中國科學院聲學研究所 噪聲與振動重點實驗室 北京 100190)
(2 中國科學院大學 北京 100049)
(3 北京印刷學院 創新物理實驗室 北京 102600)
(4 中國科學院聲學研究所 聲場聲信息國家重點實驗室 北京 100190)
0 引言
由于擁有負等效模量、負等效密度、各向異性密度等反常物理特性,聲學超材料一經問世就引起了學術界持久、廣泛的關注[1?9]。聲學超材料由周期性排列的微結構構成,其微結構尺度遠小于聲波波長,因此可等效為均勻介質。超材料的等效參數(如:等效密度,等效模量等)與其幾何結構密切相關,故可通過改變微結構的幾何參數實現對等效物理參數的調控,從而達到對彈性波、聲波的有效調控。
1995年,美國猶他大學(The University of Utah)的Milton 教授和Cherkaev 教授首先提出五模材料(Pentamode material)這一概念,該材料在形變時僅能承受主軸方向的應力,與流體的“流動”頗為相似,因此受到了研究者的廣泛關注[10]。2008年,美國羅格斯大學的Norris 教授提出了基于五模材料的變換聲學理論,完成了利用五模材料對聲波進行調控的理論分析,也激起了廣大科研工作者對五模材料及其在聲波控制領域中的研究熱情[11]。2012年,Gokhale 等在Norris 所提出的五模材料變換理論基礎上,針對環形隱身衣,研究了理想五模材料屬性與變換映射之間的聯系,并給出常密度分布、常徑向模量分布、常切向模量分布、級數密度分布、級數徑向模量分布、級數切向模量分布以及最小各項異性模量分布等幾種環形斗篷對應的映射函數[12]。此后,五模材料在水下隱身[13?14]、梯度透鏡[15]、負折射成像[16]及水聲復路通信[17]等領域均取得了進展。
原則上,基于五模材料的聲學隱身衣應具有連續的物性參數。然而,受制備工藝等客觀條件的限制,很難制備出密度和模量連續變化的五模材料。作為一種簡化手段,實際制備時必須對隱身衣進行分層,層內的密度與模量是均勻分布的。
由于超材料是由周期性排列的微結構構成,在利用超材料制備隱身衣的過程中,不可避免的要對理想隱身衣進行離散分層。在離散分層的過程中,每一層的材料參數被視為均勻分布。然而,由于分層人為引入了交界面,對隱身衣性能必然會造成影響,因此研究分層對隱身衣性能的影響具有重要的理論及實際意義。Cai等[18]研究了變換函數對分層慣性隱身衣隱身性能的影響。Scandrett 等[19]對五模材料球形隱身衣的密度和模量進行優化,以提升隱身性能。張向東等[20]研究了圓柱狀五模材料隱身衣層數、層厚分布等分層因素對隱身衣性能的影響。然而,以上工作所涉及的分層方式均為均勻分層,而對于非均勻分層的情況,目前討論并不多見。由于非均勻分層突破了分層厚度的限制,對隱身衣性能的影響多了一個自由度,因此有必要對其進行深入的研究,以便尋找最優的分層優化方案。
本文分析了分層方式對隱身效果調控的影響,提出了一種基于遺傳算法的五模材料分層優化策略,利用聲學仿真證明了該策略對窄帶探測信號和寬帶探測信號的有效性。本文所提出的分層優化策略具有易于實現,通用性強等優點,為其他類型的超材料器件設計提供了可行的技術途徑。
1 五模材料的變換聲學理論
二維空間中五模材料的彈性張量可以表示為

其中,S是五模材料的特征應力張量,在主軸坐標系下有較為簡單的對角矩陣形式:
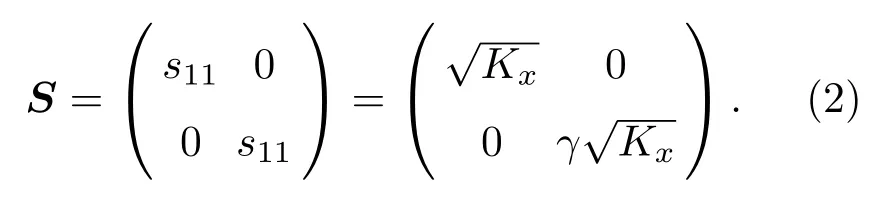
聯立公式(1)和公式(2),可以得到彈性矩陣C在主軸坐標系下有如下形式:
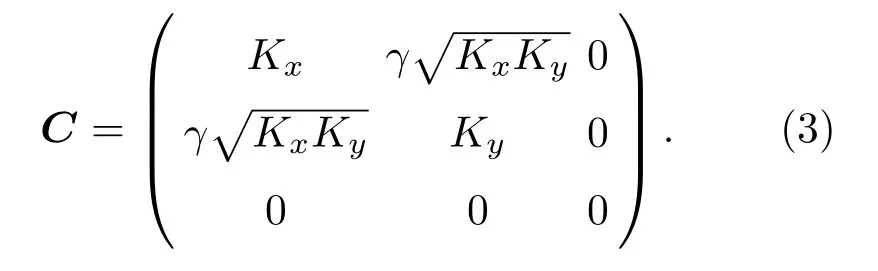
根據系數γ的正負可以進一步定義正五模材料(γ=1)和負五模材料(γ=?1),本文主要討論正五模材料,因此如無特別說明,下文五模材料均指正五模材料。公式(3)中的Kx和Ky分別為五模材料x主軸和y主軸的壓縮模量,在這兩個主方向聲波的相速度分別為
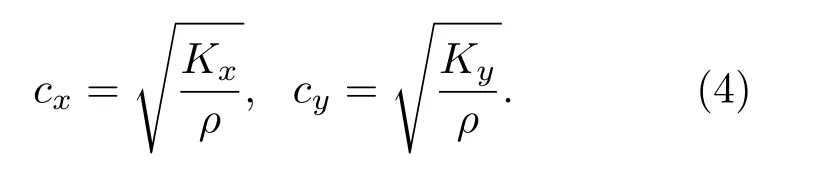
根據以上分析,改變五模材料的模量或者密度,可以實現對聲速的有效調節,這是五模材料聲波調控的基礎。
二維五模材料的微結構呈六邊形,如圖1(a)所示,其中橘黃色區域是一個完整的五模材料單元示意圖。五模材料單元的基材一般采用硬質金屬,如鋁合金、鈦合金等,六邊形內部的空白填充空氣。圖1(a)中的五模材料微結構基材為鋁合金,楊氏模量為Es=69 GPa,泊松比為σ=0.33,密度為ρs=2700 kg/m3,單元的幾何參數為l=h=5 mm,w=2.38 mm,s=3.50 mm,t=0.25 mm,因此單元的等效密度為ρeff=1263.48 kg/m3。圖1(a)中的五模材料的頻散曲線如圖1(b)所示,其中橘黃色曲線代表結構的剪切模態,綠色曲線代表結構的壓縮模態。根據圖1(b)中的能帶可以計算出微結構壓縮模態的等效聲速分別為cx=805.34 m/s,cy=1115.21 m/s,剪切模態的等效聲速分別為csx=86.34 m/s,csy=73.35 m/s。因此,通過計算可以得到該單元的等效彈性張量近似為

其中,B=2.25 GPa是水的體模量。結合圖1(b)中的頻散曲線和等效彈性張量CPM,不難發現五模材料的剪切模量遠小于壓縮模量,因此在很寬頻率范圍內結構中只存在壓縮模態,表現出近似流體的聲學特性。等效壓縮模量表現出各向異性的特征,這是因為該結構所選取的質量塊對稱性較低,可以通過調節結構單元水平邊和斜邊的長度比h/l和拓撲角β來改變各向異性程度[21]。

圖1 二維五模材料微結構和能帶Fig.1 The unit cell and band diagram of pentamode materials
通過以上分析可知,五模材料微結構的等效參數能夠很好地描述五模材料微結構的性能,因此在設計五模材料器件的過程中,常常先研究等效參數描述下五模材料器件的性能,在此基礎上進一步探究包含微結構的五模材料器件聲學效果。
2008年,Norris 教授基于空間坐標變換提出了基于五模材料的變換聲學理論,為五模材料的器件設計提供了理論基礎。該理論建立了物理空間與虛擬空間的坐標變換關系,通過對隱身衣材料進行參數設計,來操控聲波繞過隱藏區域最終實現聲隱身。
圖2(a)為二維環形五模材料的虛擬空間,圖2(b)為其物理空間,灰色的背景區域均為相同的背景介質。虛擬空間和物理空間之間可以建立如下映射關系:

圖2 五模材料坐標變換示意圖Fig.2 Diagram of coordinate transformation of pentamode material
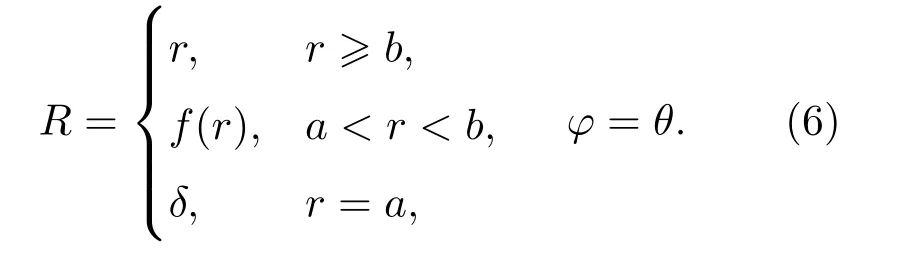
由于虛擬空間和物理空間具有不同的拓撲屬性,為了避免出現奇點,在虛擬空間的中心處挖半徑為δ的小洞,映射的邊界條件應滿足b=f(b)、δ=f(a)。映射梯度F在極坐標系下可以表示為

由于F是對稱張量,可令特征應力張量滿足

假定整個虛擬空間和物理空間中隱身衣以外的區域均分布著密度為ρ0模量為K0的聲學介質,隱身衣密度為ρ,徑向模量為Kr,切向模量為Kθ。由于聲波在兩個空間遵從相同的物理定律,波動方程具有相同的形式,結合坐標變換法則可以計算出隱身衣材料參數的表達式如公式(9)所示:
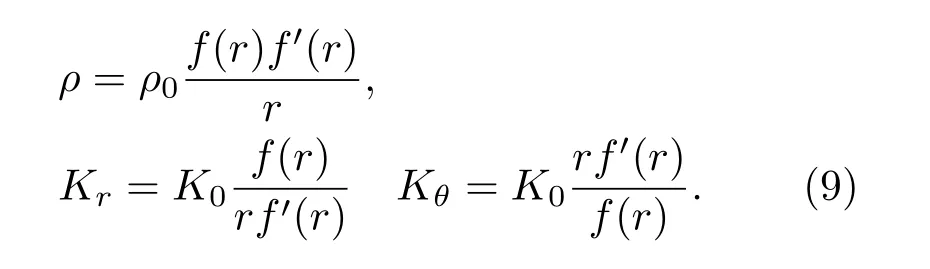
由式(9)可以看出,隱身衣的密度和模量分布取決于映射關系f(r)。表1給出了常密度映射、常模量映射和線性映射3 種具有代表性的坐標變換映射方式以及對應的參數分布。表中的密度ρ、徑向模量Kr、切向模量Kθ均為與背景介質的密度ρ0和模量K0的相對值[21]。

表1 幾種典型的映射關系Table 1 Mapping relations
2 基于遺傳算法的五模材料分層優化
表1給出了不同的映射方式對應的參數分布特點,對于設計五模材料隱身衣具有很好的指導意義。在利用表1所給出的參數設計隱身衣器件時,需要先對其進行分層。為了簡單起見,本文僅考慮標準環形隱身衣的分層優化問題。對某一層而言,層內的密度與模量視為均勻分布。以起始半徑和終止半徑的算術均值視為該層的參數半徑,然后將其代入表1的線性映射關系中,則能夠計算出該層對應的模量和密度。圖3(a)為將二維五模材料隱身衣分為5 層后的結構示意圖,其中隱藏空間的半徑r0=0.1 m,隱身衣的外徑r5=0.5 m;由內到外每一層的終止半徑分別為r1、r2、r3、r4和r5。圖3(b)~(d)分別為表1中3 種映射關系下隱身衣的密度、切向模量和徑向模量隨半徑變化的對比圖。由上述3 幅圖可知,無論是在常密度、常模量還是線性映射下,五模材料隱身衣的材料參數都是隨半徑連續變化的,且材料參數和半徑之間并不都是簡單的線性關系,這意味著隱身衣的分層方式會對其最終的隱身效果造成一定的影響,傳統的均勻分層方式并不是最優的選擇。因此,為了得到最佳的隱身效果,本文以表1所示的線性映射為研究對象,對基于五模材料的聲學隱身衣的分層方式進行了研究。

圖3 五模材料隱身衣分層示意圖和材料參數分布Fig.3 The diagram and material parameter distributions of pentamode materials
考慮到五模材料的散射聲壓場求解過程十分復雜,不易抽象出明確的散射聲壓的解析表達式,傳統的基于梯度的優化算法并不適用,故引入遺傳算法對五模材料進行分層優化,以提升隱身效果。遺傳算法是模擬生物在自然環境中的遺傳和進化過程而形成的一種自適應全局優化概率搜索算法[22]。遺傳算法最初是借鑒了進化生物學中的一些現象而發展起來的,這些現象包括自然選擇(Selection)、交叉(Crossover)以及變異(Mutation)等。遺傳算法是通過隨機生成一組目標函數作為父代樣本,經過自然選擇確定保留以及淘汰的個體,隨后再進行雜交以及變異獲得子代樣本,與自然進化進程類似,子代個體比父代個體獲得更好的適應性。
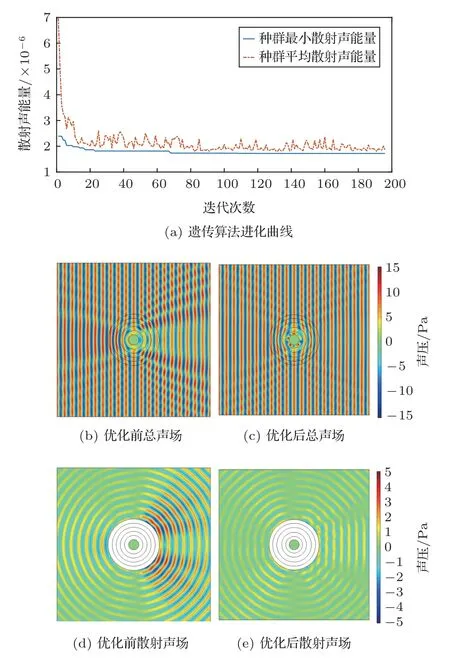
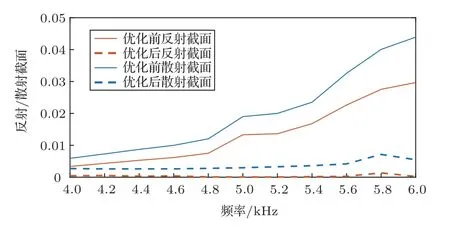
遺傳算法的流程如圖4所示,通過選擇、交叉、變異等步驟,并進行循環,達到收斂條件后即可得到最優解。在優化過程中保持隱身衣的隱藏空間的半徑r0和隱身衣的外徑r5不變,待優化變量為中間層的半徑r1、r2、r3和r4,且滿足r0 圖4 遺傳算法流程示意圖Fig.4 The capability of genetic algorithm 首先選擇最小化隱身衣的散射聲能量Es作為優化問題的目標,最小化隱身衣的散射聲能量可以用于抵御聲場中任何位置的探測。基COMSOL 進行遺傳算法優化[23],計算不同分層方式對應的散射聲能量,并在此基礎上構造適應度函數。算法對該優化問題展現出較好的魯棒性,并隨迭代次數的增加逐漸收斂。圖5(a)為目標頻率為10 kHz 時算法的進化曲線,在優化計算的過程中,迭代超過60次時已經出現了最優解,此后便是優勢逐漸擴大的過程。 優化前后隱身衣的分層方式如表2第一列和第二列所示,優化前為均勻分層,而優化后的隱身衣每一層的厚度不再均勻。隱身衣優化前后的總聲場和散射聲場可以由COMSOL進行數值仿真得到,數值模擬的區域是一個邊長為3 m 的正方形區域,背景介質為水。入射波為從仿真區域左側入射的10 kHz 的平面波,總的入射聲能量Ein可以通過入射聲場對入射邊界積分求得。為了模擬理想狀態無限大流體介質中平面聲波的傳播特性,正方形區域的4 條邊均設置為“平面波輻射”的邊界條件。隱身衣的總散射聲能量Es可以通過散射聲場對正方形區域的4 條邊界積分求得。圖5(b)和圖5(c)分別為優化前后總聲場的仿真結果,圖5(d)和圖5(e)分別為優化前后散射聲場的仿真結果。通過對比這4 幅圖可以較為直觀地看出,優化前由于存在比較嚴重的散射效應,造成總聲場的波陣面發生變形。而優化后散射聲場被明顯削弱,總聲場的波陣面更加連續,與平面波聲場更接近,隱身效果更好。 圖5 進化曲線和優化前后聲場對比Fig.5 Evolution curve and comparison of the acoustics fields before and after optimization 為了定量地展現優化前后的性能提升,常用散射截面σs來描述隱身衣的隱身效果: 其中,Ein為入射聲能量,Es為散射聲能量,散射截面σs正比與散射聲能量Es,散射截面越小,隱身效果越好。圖6展示了優化前后隱身衣散射截面隨頻率的變化曲線,與未優化的時均勻分層的隱身衣(藍線)相比,優化后隱身衣的散射截面(紅線)在以10 kHz 為中心頻率一定寬度的頻帶內整體均有所降低。其中,目標頻率10 kHz 處的散射聲能量較優化前降低了77%。由此可見,基于單目標頻點的遺傳算法優化不僅可以使目標頻點的散射聲壓大幅度降低,以目標頻點為中心的一定帶寬內的散射聲壓也會隨之被降低。 圖6 優化前后隱身效果對比Fig.6 Comparison of the stealth effects before and after optimization 為了拓寬優化頻帶的寬度,躲避寬頻聲吶信號的探測,也可以對多個頻點的散射聲場同時進行最小化。這里選取目標頻率點為9 kHz、10 kHz 和11 kHz,優化后的隱身衣每一層的半徑如表2第三列所示,優化后隱身衣散射截面隨頻率的變化曲線如圖6中黃線所示。與圖6中紅線對比可知,雖然單目標優化可以令f=10 kHz 處的散射聲能量降得很低,但偏離10 kHz 時散射聲壓會稍有提升;若對9 kHz、10 kHz、11 kHz三個頻率點同時進行優化,在更加寬頻的范圍內的散射聲能量均被降低了,且散射聲能量的變化趨勢也更加平緩。 表2 優化前后隱身衣每一層的半徑Table 2 The radius of each layer of pentamode materials before and after optimization(單位:m) 現階段使用的聲吶探測儀多為自發自收型,考慮實際需求只需要最小化回波能量,即反射聲能量,就能躲避自發自收型水下聲吶信號探測,獲得很好的隱身效果。 假定探測信號為由仿真區域左方入射的5 kHz的平面波,優化目標為最小化反射聲能量,即最小化左半邊區域的散射聲能量。整個優化過程與數值仿真方法與2.1 節完全相同,其中隱身衣的反射聲能量Er可以通過散射聲場對左半邊區域的邊界積分求得。圖7為優化前后散射聲場分布對比,可以看到優化前散射聲場能量有很大部分集中在左側回波部分,而對分層方式進行優化可以使散射聲場能量幾乎全部集中在透射區域,從而大大降低回波強度,隱身性能得到大大加強。 圖7 優化前后散射聲場對比Fig.7 The comparison of the scattering fields before and after optimization 與2.1 節中的散射截面類似,這里定義反射截面σr來定量地描述反射聲場的強度: 其中,Er為反射聲能量,反射截面σr正比于散射聲能量Er,反射截面越小,在入射端進行探測時越不易探測到,隱身效果越好。 圖8為優化前后反射截面和散射截面隨頻率的變化曲線的對比,實線代表優化前的仿真結果,虛線為優化后的仿真結果。由圖8可知,在目標頻率附近的反射聲能量得到了明顯的抑制,反射能量降低了90%以上。值得注意的是,壓低反射區域聲能量的同時并不會造成透射區域聲能量的增高,整個背景聲場的散射聲能量也均比優化前有所降低。 圖8 優化目標為最小化反射聲能量時隱身效果對比Fig.8 Comparison of stealth effect for minimizing reflected acoustic energy 綜上所述,在實際應用時可以考慮探測信號的類型,來設置優化目標,以達到最優的隱身效果。 作為一種能夠傳播縱波而抑制橫波的等效流體,五模材料擁有寬頻有效性、固體形態、模量和密度同時可調、基體介質選擇多樣等優點,因此常被用于水下聲波調控。基于五模材料的變換聲學理論的問世使五模材料成為制作水下聲隱身斗篷的熱門材料之一,逐漸獲得了國內外研究組的廣泛關注。本文基于Norris 教授提出的五模材料變換聲學理論,提出了五模材料隱身衣分層優化策略,并利用COMSOL 進行了聲學仿真。仿真結果表明優化前的均勻分層并不能得到最理想的隱身效果,而采用優化策略后散射聲能量和反射聲能量都有大幅下降,對于窄帶和寬帶探測信號都具有更好的隱身效果。 由于超材料的微結構設計是一個十分復雜的問題,很難得到確切的解析解,而在對數值解的探索方面尚有很多問題亟待解決。鑒于遺傳算法在五模材料的分層優化問題上取得了較好的效果,且具有原理簡單、易于實現、通用性強等優點,在之后的研究中將會在分層優化的基礎上加入微結構單元,進一步推動超材料從理論模型邁向實際應用。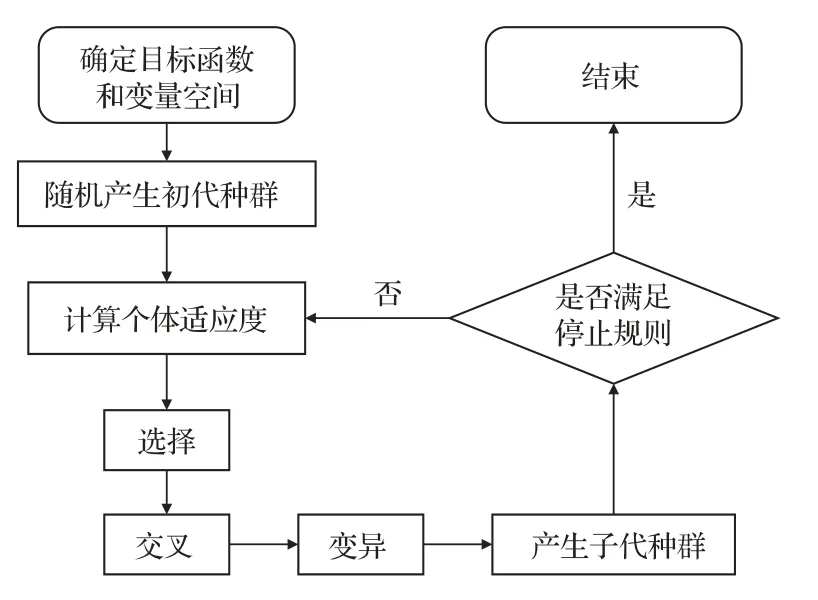
2.1 最小化散射聲能量



2.2 最小化反射聲能量


3 結論

