基于KIVA機器人的緊致型倉儲系統待命位策略研究

□ 王 婧,孫子文

(武漢科技大學 恒大管理學院，湖北 武漢 430065)

1 引言

隨著城市人口密度越來越大，土地資源也越發緊張，高昂的土地成本持續促進倉儲系統發展；同時，電子商務蓬勃發展，呈現出批量小、品類多、海量化、注重實效以及實時變化等特點，對倉儲系統提出了更高的要求。如何在保持較高空間利用率的情況下，兼顧期望取貨時間以及訂單響應速度，是自動化倉儲系統發展需要解決的重要問題。目前，關于倉儲管理的研究越來越多，且越來越集中在緊致化和智能自動化倉儲系統上。從采用自動牽引小車AGV的智能倉儲系統[1]，到亞馬遜推出的KIVA機器人系統[2],這類物至人揀貨系統由于具有較高的取貨率，經過多年的發展，已經成為物流業智能倉儲系統主要的取貨方式之一[3]。KIVA系統雖然極大地縮減了取貨時間并提高了取貨率，但是其空間利用率較低，在此基礎上，Gue等[4]提出了一種高密度倉儲系統，極大提升了空間利用率，但取貨時間較長。

在傳統的倉儲系統中，一般采用的是人至物的取貨流程，即揀貨人員從I/O點出發，到達目標取貨點取貨并返回出庫點，這種取貨方式的取貨時間大部分花在了取貨人員的行走上[5]，而在智能倉儲系統中，通過KIVA機器人或AGV取貨的物至人取貨系統，可極大縮減取貨時間，并提高取貨率和準確度[6]。為了進一步提升智能倉儲系統的效率，許多學者對智能機器人的待命位進行了優化。Egbelu和Wu通過系統仿真的方法，比較了兩種不同倉儲方式下多個待命位策略的取貨效率[7],徐賢浩、郭依等以取貨時間最小化為目標，提出了三種待命位策略，并比較了三種不同待命位策略的優劣[8]。

現階段,以KIVA機器人系統為基礎的自動化智能倉儲系統都具有較高的取貨率，但其空間利用率較低。相比KIVA系統，Gue提出的網格倉儲系統有著較高的空間利用率，但隨著倉儲規模的擴大，其取貨效率逐漸降低，訂單反應時間也在增加。電子商務發展到今天，各種電商企業的倉庫對自動化智能倉儲系統各方面的要求越來越高，小批量的訂單、海量化的品類、昂貴的土地成本等因素都要求倉庫必須提升空間使用率，注重訂單時效及顧客滿意度等因素都需要智能倉儲系統降低取貨時間、提高取貨效率。因此，本文基于KIVA機器人系統提出了一種緊致型倉儲系統，在考慮空間利用率的情況下，兼顧降低取貨時間和提高取貨效率，并比較不同待命位策略下的取貨時間以及不同系統的空間利用率和系統容量。

2 問題描述

本文提出的緊致型自動化倉儲系統布局如圖1所示。在此系統中，取貨與補貨等操作都由KIVA機器人完成，相比于人工操作，縮短了取貨時間，提高了精確度，降低了人工成本。該系統一次完整的取貨周期如下：處于待命位的機器人收到取貨指令后，從待命位出發行駛至目標貨架，同時倉庫內幫助進行翻箱操作的機器人同時移動，并進行翻箱操作，機器人將目標貨架取出，送至取貨口，揀貨員在出貨口完成揀貨操作后，機器人將貨架送回原位，最后機器人回到待命位等待下一個取貨指令。

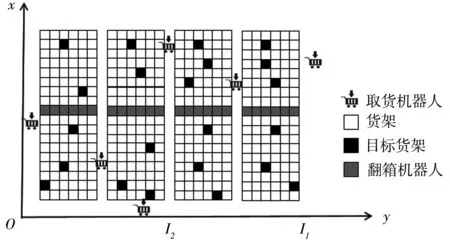
圖1 緊致型倉儲系統布局示意圖

此系統布局與KIVA系統布局相似，有多條縱向通道，但為提升空間利用率，系統中只設置了兩條橫向通道，機器人在通道內行駛取貨。本文研究了此系統的三種待命位策略：①取貨完成并返還貨架后機器人返回待命位I1點；②取貨完成并返還貨架后機器人返回待命位I2點；③取貨完成并返還貨架后機器人直接停留在原處。

3 模型構建

3.1 模型假設及符號說明

基本假設：①有足夠多的機器人保證翻箱操作及取貨操作的流暢性，機器人的數量不作為制約取貨時間的因素；②在此系統中，機器人若要取內層貨架，則需要進行翻箱操作，因本文假設有足夠多的機器人輔助進行翻箱操作，故不考慮翻箱操作所花費的時間；③每一個貨架被取到的概率都相等，即采用隨機倉儲策略；④忽略機器人轉向時間以及舉起和放下貨架的時間；⑤機器人的行走速度比人的移動速度快，且勻速移動，不考慮加速和減速的影響；⑥圖1中I1和I2既是待命位，也是出貨口。

符號說明如表1所示。

表1 符號說明

3.2 待命位在I1點的平均取貨時間模型

本文以子模塊列數為6的緊致型倉儲系統為例。在待命位為I1點的待命位策略下，一次完整的取貨流程為：KIVA機器人收到取貨指令后向目標貨架移動，完成取貨并返還貨架，最終返回待命位。在此取貨過程中，KIVA機器人進行了4次橫向移動和4次縱向移動，且每次縱向移動時間相同，橫向移動時間也相同，用Tx1表示每次橫向移動的時間，用Ty1表示每次縱向移動的時間，則總的取貨時間可以表示為

T1=4Tx1+4Ty1

(1)

建立一個如圖1所示的直角坐標系，假設I1的坐標為(M1,0)，則橫坐標的值為M1=ndl+6nb，假設目標貨架M的坐標為Mi,j，其中i,j分別表示貨架的行數和列數，此時可得到機器人的每次橫向平均移動時間為：

(2)

將公式(2)化簡后可得：

(3)

KIVA機器人在縱向移動過程中，由于任意一行貨架到出貨點的垂直距離都相等，因此當行數確定時，每一次縱向移動時間可表示為

(4)

將公式(3)(4)帶入公式(1)，則可得到在此待命位策略下總的取貨時間：

(5)

3.3 待命位在I2點的平均取貨時間模型

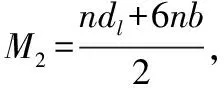
T2=4Tx2+4Ty2

(6)

(7)

由于縱坐標未改變，KIVA機器人的縱向移動時間與第一種策略相同：

(8)

將公式(7)(8)帶入公式(6)，可得到第二種待命位策略下的平均取貨時間：

(9)

3.4 第三種待命位策略下的平均取貨時間模型

分析以上兩種待命位可知，第二種待命位策略即待命位在I2時，取貨時間相對較短，所以應選取I2點作為第三種待命位策略的待命位點和出貨口。在此待命位策略下，一次完整的取貨流程：KIVA機器人收到取貨指令后向目標貨架移動，完成取貨并返還貨架，最終停留在貨架返還處。在此取貨過程中，KIVA機器人進行了3次橫向移動和3次縱向移動，且每次縱向移動時間相同，橫向移動時間也相同，用Tx3表示每次橫向移動的時間，用Ty3表示每次縱向移動的時間，則總的取貨時間可以表示為

T3=3Tx3+3Ty3

(10)

將公式(7)和(8)帶入公式(10)，得到第三種待命位策略下總的取貨時間：

(11)

4 數值實驗與結果分析

4.1 模型驗證

為了驗證模型的有效性，參考徐賢浩等[8]研究的倉儲系統，假設緊致型倉儲系統中的基本參數為a=1.5,b=3,dl=1.2,dw=1.2。鑒于緊致型倉儲系統的布局特點，可通過同時改變縱向通道數量、貨架行數來改變系統規模的大小。在此基礎上，設置1、2、3三種不同的場景，并在計算機中對三種不同的場景分別進行模擬取貨操作，每次模擬進行200次取貨操作，共模擬N次，最后計算模擬結果的平均值，并將其作為總的取貨時間，可得到三種待命位策略的模型結果與仿真結果，如表2所示。

表2 模型結果與仿真結果

由表2可知，緊致型倉儲系統在三種不同待命位策略下，KIVA機器人取貨時間的模型結果與仿真結果的相對誤差較小，最高只有5.15%，并且隨著模擬次數的增加，相對誤差也在縮小，因此模型的有效性得到了驗證。

4.2 結果分析

改變系統面積，對本文提出的緊致型倉儲系統與傳統布局KIVA系統中的機器人平均取貨時間進行研究，然后通過MATLAB模擬仿真，得到兩種系統在三種不同待命位策略下的平均取貨時間，如表3所示。

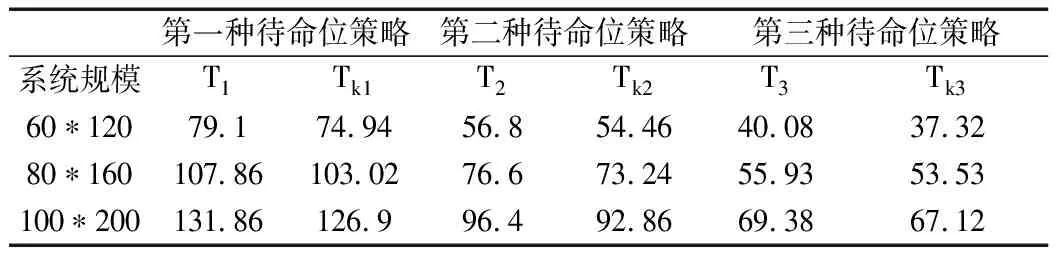
表3 三種待命位策略下緊致型倉儲系統與KIVA系統的平均取貨時間

在表3中，T1、T2、T3分別表示三種待命位策略下緊致型倉儲系統的平均取貨時間，Tk1、Tk2、Tk3分別表示三種待命位策略下KIVA系統的平均取貨時間。觀察表中數據可知，緊致型倉儲系統的平均取貨時間比KIVA系統要多2s到5s，這是因為當系統容量較小時，即使有翻箱機器人輔助進行翻箱操作，翻箱時間還是會影響取貨時間，但當系統容量逐漸增大時，翻箱時間對取貨時間的影響可以忽略不計，緊致型倉儲系統的平均取貨時間將與傳統的KIVA系統的取貨時間相同。

除了取貨時間及取貨效率以外，倉儲系統的空間利用率、系統容量也處于重要地位，因此，對兩種系統的空間利用率及系統容量進行比較是很有必要的。同時，由于倉儲系統的空間利用率及系統容量取決于系統布局，待命位點的設置對其影響甚微，因此不用考慮待命位策略，可以直接進行比較。如圖2所示，緊致型倉儲系統和KIVA系統的空間利用率分別為81%和56%左右，前者空間利用率比后者高出將近25%左右；其次，如圖3所示，當系統規模相同時，KIVA系統的容量是小于緊致型倉儲系統的，并且系統容量的差值隨著系統規模的增大而增大。

圖2 空間利用率比較

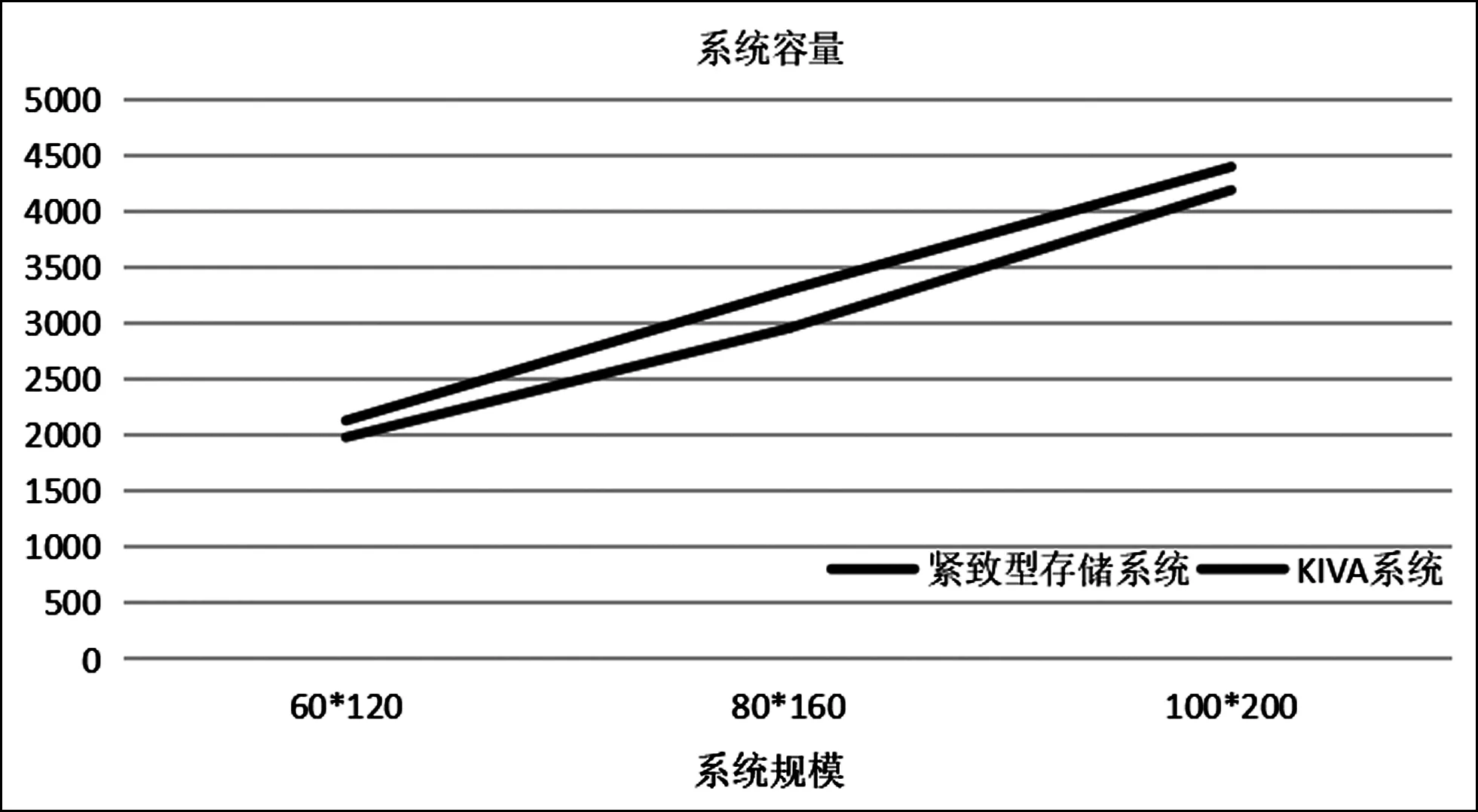
圖3 系統容量比較

此外，由T1

5 結論

本文在KIVA機器人智能倉儲系統基礎上提出了一種緊致型倉儲系統，并根據三種不同的待命位策略分別建立了取貨時間模型，驗證了模型的有效性。通過對緊致型倉儲系統和KIVA機器人系統在三種不同待命位策略下的取貨時間、系統空間利用率以及系統容量進行比較，發現緊致型倉儲系統各方面性能均優于KIVA系統。然而，此系統需要較多數量的機器人進行翻箱和取貨操作，這會提升機器人采購成本，不過隨著科技進步，機器人的制造成本必定會逐漸下降，而土地成本和人工成本將來會越來越高，綜合來看，基于KIVA機器人系統的緊致型智能倉儲系統相對于傳統的KIVA機器人系統會為企業節省更多的成本。因此，基于KIVA機器人的緊致型智能倉儲系統有一定的現實意義。本文只研究了一個待命位的不同策略，也并未考慮機器人取貨排隊及擁堵問題，未來可以研究多個待命位同時取貨以及排隊等問題。