鐵海聯運煤炭供應鏈的數學建模與案例分析*

□ 紀曉彬，劉仕強

(福州大學 經濟與管理學院，福建 福州 350108)

1 引言

煤炭被譽為“黑色黃金”，是社會生產與生活中不可或缺的重要能源[1]，現代煤炭企業的競爭已經不再局限于煤炭企業之間的競爭，而是滲透于企業所處的煤炭供應鏈的角逐之中，為了使煤炭企業在市場博弈中保持優勢與生命力，必須加強其煤炭供應鏈的核心競爭力[2]，隨著煤炭行業的發展，煤炭供應鏈也備受國內外學者專家的關注[3]，傳統的煤炭供應鏈網絡CSCN(Coal Supply Chain Network)主要以確定性情境為假設，其研究范圍包括煤炭采購、配煤加工、煤炭銷售、煤炭供應鏈的網絡設計等。然而這種假設在復雜多變的市場條件面前顯然缺乏合理性。近兩年，受到新冠疫情的持續影響，商品和原材料需求激增[4]，電力企業所需煤炭需求量增加，同時，疫情的反復導致港口擁堵和船期延誤，危及全球煤炭供應鏈的順暢進行，影響到各個行業的發展[5]。在國際上，2021年7月，受到國際市場需求上漲的影響，動力煤價格周環比繼續上漲，導致印度煤炭進口量持續低迷，燃煤庫存告急，部分電廠因缺煤幾近關停；同月，列車脫軌事件導致兩條通往南非理查茲灣煤碼頭(RBCT)的運煤鐵路被迫停運，需進行檢修，印度8月至9月下旬的平均每周煤炭進口量低于150萬噸，為至少兩年來最低，全球煤炭價格上漲了40%以上，創下歷史新高；我國是煤炭消耗大國，能源經濟的長期安全對于滿足公民對終端能源服務的需求至關重要，在國內，由于煤價上漲以及疫情影響減弱，經濟復蘇，眾多行業需求增長導致電力供應緊張，1至8月煤炭進口量約下降了10%；由于部分高耗能產業“西遷”、風電驟減等，9月份多地對高耗能高排放企業采取“拉閘限電”等政策來改善電力供需緊張的局面；此外，十一黃金周期間，山西這個產煤大省遭遇百年難遇洪災，多個煤礦基地被洪水倒灌導致停產，損失慘重。因此，在不確定條件下，煤炭供應鏈相關企業如何制定與選擇最優決策以保證煤炭供應鏈的順暢進行，對于企業本身、社會乃至國家都有巨大影響，本文主要針對不確定條件下的煤炭供應鏈網絡進行研究，意在降低CSCN總運營成本的同時，提高CSCN的抗風險能力。

關于CSCN的研究最早起源于煤炭物流設施選址問題，國內外較多學者針對的是確定情景下的煤炭供應鏈網絡的研究。Sun等[6]探討煤炭區域供應鏈，利用多區域投入產出模型(MRIO)對中國礦產資源需求進行分析；Valderrama等[7]設計了一個整合經濟與環境的煤炭供應鏈模型，驗證了供應鏈中不同成本和運輸排放量之間的顯著關系；Bowen等[8]建立了一個斯塔克爾伯格模型，評估基于兩級價格管制的煤電供應鏈的戰略熱訂單實現率；李丹等[9]考慮整體利潤和客戶滿意度，提出了煤炭供應鏈多目標優化模型，利用廣義遺傳算法進行求解；Wang等[10]運用有向復雜網絡模型來考察全球煤炭貿易體系的演變，討論了可持續發展的潛在有效策略；袁旭梅等[11]考慮港口物流服務能力，建立了海運煤炭供應鏈的網絡多目標模型，并引入“成本關系系數”進行求解；Dong等[12]針對大型發電集團煤炭海運供應鏈，構建模型以達到最小化采購及運輸總成本的目的。上述研究限于確定情境下的CSCN，且大多是以單一運輸方式進行研究[13]，在戰術層面結合多種運輸方式的研究并不多，然而不同運輸方式下的成本與選擇會對供應鏈全局產生影響[14]，中國特殊的煤炭分布情況導致煤炭運輸主要由鐵路完成，鐵路有限的運輸能力以及高昂的修建和維護成本[15]促使我國開始大力推行多式聯運模式[16]，其中鐵海聯運因其成本低、運量大的優勢，逐漸成為中國最重要的煤炭運輸方式之一。本文在對CSCN進行研究時，將其設定在鐵海聯運條件下進行的運輸。

國內外對于不確定條件下的煤炭供應鏈的研究相對較少，由于實踐中數據與參數均存在不確定性，本文考慮需求和煤炭價格不確定情境下的煤炭供應鏈問題。在眾多文獻中，常常采用隨機規劃法、模糊規劃法、魯棒優化法等方法處理不確定情景下的供應鏈問題[17]；孫華麗等[18]針對物資需求量和車輛運輸時間的不確定性，建立應急設施選址-路徑魯棒優化模型；李彤等[19]針對不確定需求下的取貨問題，建立新的基于實際需求的路徑-裝載協同優化模型并進行求解；樓振凱等[20]針對二級供應鏈中的不確定信息，建立Stackelberg魯棒博弈模型；鄧燁等[21]同時考慮需求不確定及風險情景增量不確定的閉環供應鏈選擇問題，利用模糊機會約束法進行研究和求解；樂美龍等[22]針對航空公司的樞紐航線網絡規劃問題，采用隨機規劃法研究其在機場的容量份額；范厚明等[23]結合模擬退火算法與粒子群算法，通過隨機規劃法，探討需求以及港口建設成本不確定情景下的港口失效問題；劉家國等[24]分析信息不對稱、需求不確定下零售商公平偏好的價值和策略行為；張學龍等[25]考慮需求不確定，基于需求與產品單價的區間灰色特征，建立魯棒優化模型并進行求解。綜上，本文圍繞CSCN設計問題，以提高整個煤炭供應鏈系統的運營效率以及節省運作的成本[26]同時降低供應鏈運作的風險，建立了考慮煤炭需求不確定性情景下的CSCN魯棒優化設計模型。

本文的主要工作與貢獻有以下四點：

第一，在研究對象上，本文基于煤炭供應鏈全局的視角，研究了以煤炭生產地為起點，經過煤炭中轉港、煤炭目的港，最終到達煤炭消費地的煤炭運輸問題，在目標函數與約束條件中均考慮了港口的庫存問題，以最小化綜合運輸成本為目標函數建立優化模型，提供更加全面的決策方案。

第二，在運輸方式上，本文不再考慮單一運輸方式下的煤炭供應鏈問題，而是基于近幾年國家大力發展的“鐵海聯運”模式，構造鐵運+海運聯合運輸下的煤炭供應鏈模型，根據使用鐵海聯運方式的實際情況，構建多階段煤炭供應鏈網絡。

第三，在研究內容上，本文探討并分析了不確定情景條件下的煤炭供應鏈問題，利用情景規劃法建立了煤炭需求與煤炭價格不確定情景下的魯棒優化模型，從煤炭供應鏈全局的角度優化不同情境下的煤炭運輸與調配方案。

第四，在實際運用中，本文以包頭、鄂爾多斯、神木為煤炭生產地，將秦皇島、天津港、舟山港等國內重要港口設置為中轉港口，為大型煤炭企業的決策者選擇合適的中轉港口并設置庫存提供更好的決策，有利于防控不確定環境影響下的需求及煤價波動帶來的風險。

2 不確定需求下煤炭供應鏈網絡優化的數學建模

2.1 問題描述與假設

本文所研究的煤炭供應鏈網絡由提供煤炭的露天煤礦或礦井開采地、配煤中心、倉儲企業、物流運輸企業及煤炭消費方組成；由于國家大力推行鐵海聯運模式，因此將鐵海聯運作為本文所設計的煤炭供應鏈的運輸方式，其中涉及到了煤炭運輸的四個階段，分別是煤炭生產、鐵路運輸、海上運輸以及消費配送[27]。煤炭供應鏈各環節所需費用包括運輸費用、中轉費用、庫存費用，目標是在滿足總費用最小的同時，降低不確定需求與庫存價格所帶來的風險，煤炭屬于大宗商品，在需求方面受地區、氣候、自然災害影響，導致煤炭需求與煤炭價格呈現季節性波動，有很顯著的不確定性，本文采用情景法來描述煤炭需求與庫存價格的不確定性。

綜上所述，煤炭需求與港口庫存價格不確定條件下CSCN問題可以描述為以最小化供應鏈的總成本和風險為目標，給定在不同情境下的需求量和港口庫存價格，求解不同情境下不同節點之間煤炭最合適的運輸路徑、煤炭調配量，選擇合適的港口進行中轉與庫存的問題。

為方便研究，在建立模型的過程中做以下假設：

①煤炭不允許缺貨，港口要有一定的安全庫存以及庫存上限保證生產運輸的連續性；

②考慮鐵路的運能上限，海路運力相對于鐵路運力較富余，不考慮海路的運力限制；

③忽略煤炭運輸過程中煤炭的損耗；

④假設煤炭生產地與煤炭起運港、起運港與目的港之間是多對多運輸，而目的港與消費地之間，每個消費地只能由一個港口輸送煤炭。

2.2 參數定義及說明

集合和下標：

I,M,J,K煤炭生產地、煤炭中轉港口、煤炭目的港口、煤炭消費地的數量

i,m,j,k煤炭生產地、煤炭中轉港口、煤炭目的港口、煤炭消費地節點，i=1,2,…,I;m=1,2,…,M;j=1,2,…,J;k=1,2,…,K

Γ不確定情境的數量

α不確定情境序號，α∈1,2,…，Γ

參數：

Pαi不確定情景α下煤炭生產地i對煤炭的供應能力

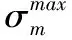
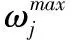
aim煤炭從煤炭生產地i至中轉港口m的單位運輸費用

bmj煤炭從中轉港口m至目的港j的單位運輸費用

cjk煤炭從目的港j到消費地k的單位運輸費用

eαi不確定情景α下煤炭生產地i的單位煤炭采購價格

Nom可選擇中轉港口m的最大數量

Ndj可選擇目的港j的最大數量

uom中轉港口m的中轉費用

udj目的港j的裝卸費用

fm中轉港口m的固定費用

capim從煤炭生產地i至中轉港口m的鐵路運能約束

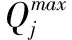
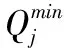
usj目的港j的單位庫存價格

Dαk不確定情景α下消費地k對煤炭的需求量

pα不確定情景α發生的概率

λ魯棒性的調整權重，反映決策者的風險偏好

τα不確定情景α下需求不能滿足時的懲罰權重

決策變量:

oαm0-1變量，判斷不確定情景α下中轉港口m是否被選中，若被選中為1，否則取0

μαj0-1變量，判斷不確定情景α下目的港j是否被選中，若被選中為1，否則取0

xαim不確定情景α下從生產地i至中轉港口m的煤炭運輸量

yαmj不確定情景α下從中轉港口m至目的港j的煤炭運輸量

zαjk不確定情景α下從目的港j至煤炭消費地k的煤炭運輸量

qαj不確定情景α下煤炭在目的港j的新增庫存量

Qαj不確定情景α下煤炭在目的港j的現有庫存量

sαjk0-1變量，判斷不確定情景α下煤炭目的港口j是否為消費地k服務，若港口j為消費地k配送煤炭為1，否則取0

θα不確定情景α下供應鏈總成本相對于期望成本的松弛變量

δαk不確定情景α下消費地k的煤炭需求的松弛變量

2.3 數學模型

魯棒優化數學模型建立在確定性需求的模型之上，根據文獻[26]提出的魯棒優化模型原型，假設每個情景α下的煤炭需求都不確定，每種情景發生的概率對應為pα，對應情景α下消費地k的需求量為Dαk，Wα表示不確定情景α下供應鏈的總成本，建立不確定需求下CSCN鐵海聯運魯棒優化數學模型：

(1)

(2)

(3)

(4)

(5)

xαim≤capim,i=1,…,I;m=1,…,M;α∈1,2,…Γ

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

qαj,Qαj≥0,j=1,2,…,J;α∈1,2,…,Γ

(15)

oαm,μαj,sαjk∈{0,1},m=1,…,M;j=1,…,J;k=1,…,K;α∈1,2,…,Γ

(16)

xαim,yαmj,zαjk≥0,i=1,…,I;m=1,…,M;j=1,…,J;k=1,…，K;α∈1,2,…,Γ

(17)

θα,δαk≥0,α∈1,2,…,Γ;k=1,2,…,K

(18)

其中，式(1)為魯棒優化數學模型的目標函數，意在最小化期望成本、風險成本及懲罰函數之和；式(2)表示供應鏈的總運營成本，由直接運輸費用、中轉費用、庫存成本、固定費用四個部分組成；式(3)為煤炭供應鏈的成本偏差約束方程，針對成本偏差松弛變量，保證不同情景下總成本的變化達到最小；式(4)表示需求松弛變量方程；式(5)表示情景α下煤炭生產基地的流量守恒約束。對于任意一個生產基地i，輸出的煤炭量之和等于其供應量；式(6)表示鐵路運能約束。情景α下從煤炭生產地i運輸至中轉港m的煤炭量之和不能超過鐵路的運輸能力上限；式(7)表示被選擇的中轉港口m的數量限制；式(8)表示起運港流量守恒限制。情景α下對任意的中轉港m，煤炭的煤炭流入量之和等于煤炭流出量之和；式(9)表示起運港下水量約束。情景α下任意一個中轉港口m，其煤炭下水總量不超過該港口的最大下水量；式(10)表示目的港配送約束。情景α下對任意一個目的港j，其煤炭總裝車量不超過最大裝車能力；式(11)表示目的港流量平衡約束。情景α下對任意一個目的港，煤炭的煤炭流入量等于流出量與新增庫存量之和；式(12)表示目的港庫存更新約束。情景α下，現有庫存量為原始庫存量與新增煤炭量之和；式(13)表示目的港庫存限制約束。情景α下，現有庫存總量不低于安全(最低)庫存，不超過最高庫存；式(14)表示情景α下每個消費地的煤炭由一個目的港口輸送煤炭；式(15)-(18)為決策變量約束。

3 案例分析

在本章中，為了驗證模型的有效性，本文針對一個煤炭企業案例，以第二章所建立的優化模型為基礎，采用IBM ILOG CPLEX Optimization Studio 12.6.0優化軟件，對所構建的混合整數規劃 (Mixed Integer Programming，MIP) 模型進行求解，將所得結果以表格與網絡圖形式進行描述。

3.1 案例描述

考慮某煤炭企業擬以包頭、鄂爾多斯、神木為煤炭生產地(即I=3),記為I1、I2、I3，秦皇島港、京唐港、天津港、黃驊港、日照港、青島港為煤炭中轉港口(即M=6)，記為M1、M2、M3、M4、M5、M6，浙江舟山港、上海港、廣東廣州港、福建廈門港、江蘇連云港為目的港口(即J=5)，記為J1、J2、J3、J4、J5，選定目的港口附近的9個電廠為主要消費地(即K=9)，記為K1、K2、K3、K4、K5、K6、K7、K8、K9。該企業的目標是通過考慮不確定需求與煤價，優化并調整煤炭供應鏈網絡，以最低的綜合運輸、庫存成本最小化為目標，增強抵御不確定風險的能力，進行科學決策。

煤炭需求有季節性波動的特點，例如冬季溫度低，進入北方供暖的用煤旺季；夏季氣候炎熱，部分地區雨水不足進入旱季導致水力發電量不足,火力發電需求量升高；新能源的大力倡導與推行壓制了火電增速，新能源對火電的替代效應正在加強，煤炭需求下降；在煤價的不確定性方面，受外界不確定影響較大，例如疫情期間電廠停業或部分倒閉，下游煤炭需求低迷，煤炭價格下跌；進入經濟復蘇期后，工業生產恢復，另外疊加港口擁堵，近期煤炭價格快速增長，居高不下，煤價的漲跌與煤炭供需關系息息相關，因此，在需求關系變化時，煤價也會隨之產生波動。分別考慮煤炭消費地的四種情景：需求疲弱、需求一般、需求較高以及需求激增的情況，將各個情景的概率分別設置為0.1，0.2、0.3、0.4，各情景下煤炭消費地的需求情況及產地的煤價如表1、表2所示。

表1 不同情景下各煤炭消費地需求量(單位：萬噸)

表2 不同情景下各煤炭生產地煤炭單位采購價(元/噸)

3.2 數據來源

本模型主要涉及的費用包括直接運輸費用、港口中轉費用、港口固定費用、庫存成本以及采購成本。直接運輸費用包括鐵運、海運的費用，由節點之間運輸的煤炭量與單位運輸成本的乘積表示，運輸費用包括鐵路運輸基金、鐵路運輸價格、電器附加費等，根據《鐵路貨物運價規則》、鐵路95306網站確定；港口中轉費用指的是為船舶運輸和貨物裝卸提供勞務的費用，即轉換運輸方式的費用，港口中轉費用由運輸的煤炭量與港口的單位中轉費用的乘積表示，單位中轉費用根據《通用集裝箱裝卸綜合作業費率表》《集裝箱貨場內搬運費率表》《港口費率表》確定；港口固定費用是指港口建設費、安保費、查驗費等，根據《港口收費方法》確定；庫存成本由煤炭在該港口的庫存量與單位庫存價格的乘積表示，單位庫存價格來源于中國煤炭交易數據網；采購成本由生產地的煤炭供應量與煤炭生產地的單位采購價格的乘積表示，單位采購價格來源于中國煤炭交易數據網。

3.3 模型計算結果

根據第二章所建立的CSCN魯棒優化模型，利用IBM ILOG CPLEX Optimization Studio 12.6.0優化軟件進行求解，表3為不同情景下煤炭供應鏈的總費用計算結果。

表3 不同情景下煤炭供應鏈的總費用(單位：萬元)

將不同情景下的鐵海聯運煤炭最優運輸路徑用網絡圖形式描述，如圖1所示。

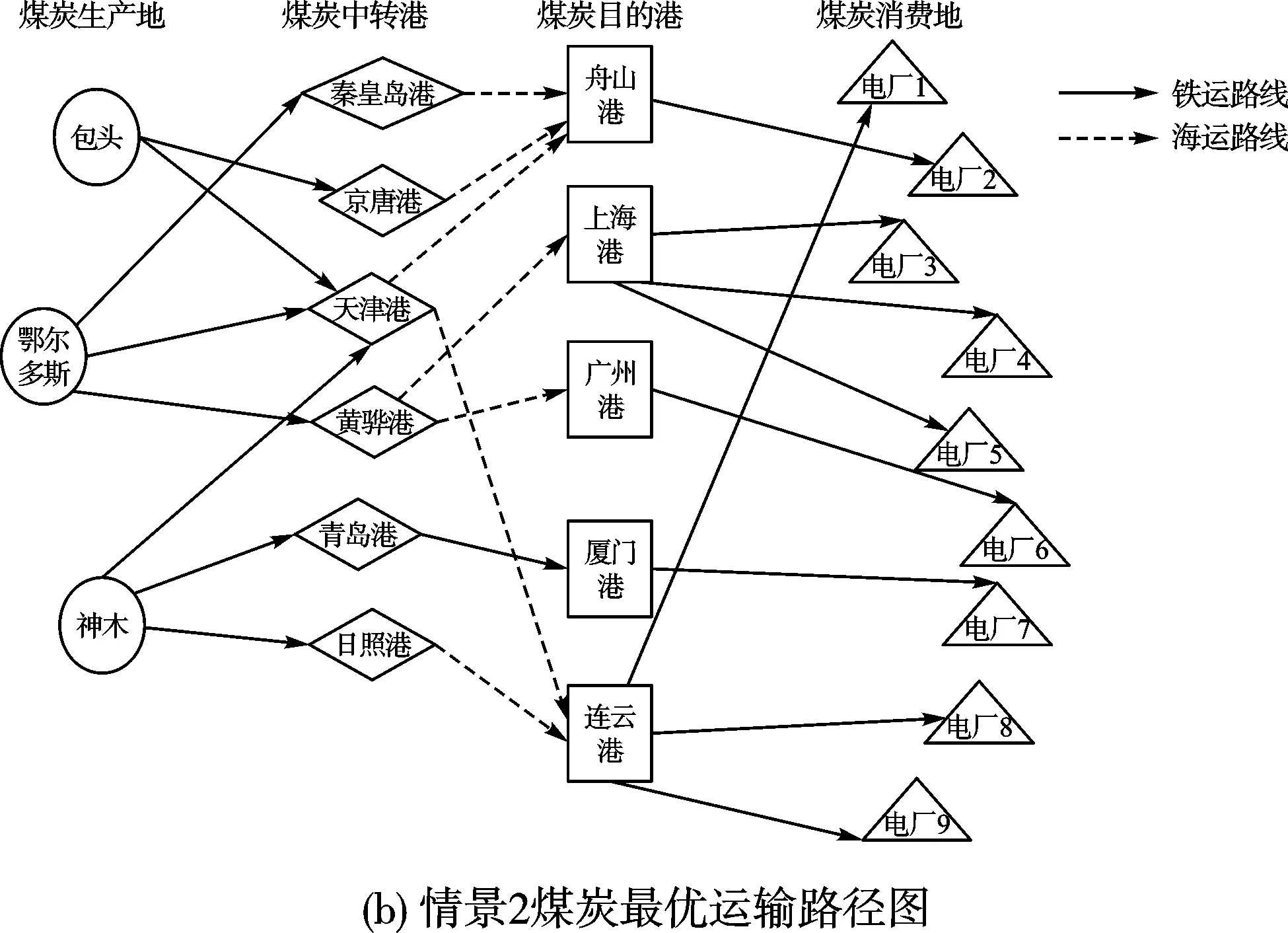
圖1 不確定下情景CSCN魯棒優化模型運行結果

圖2為不同情景下各港口的庫存變化情況，橫坐標表示各目的港口，縱坐標表示各港口煤炭庫存量。

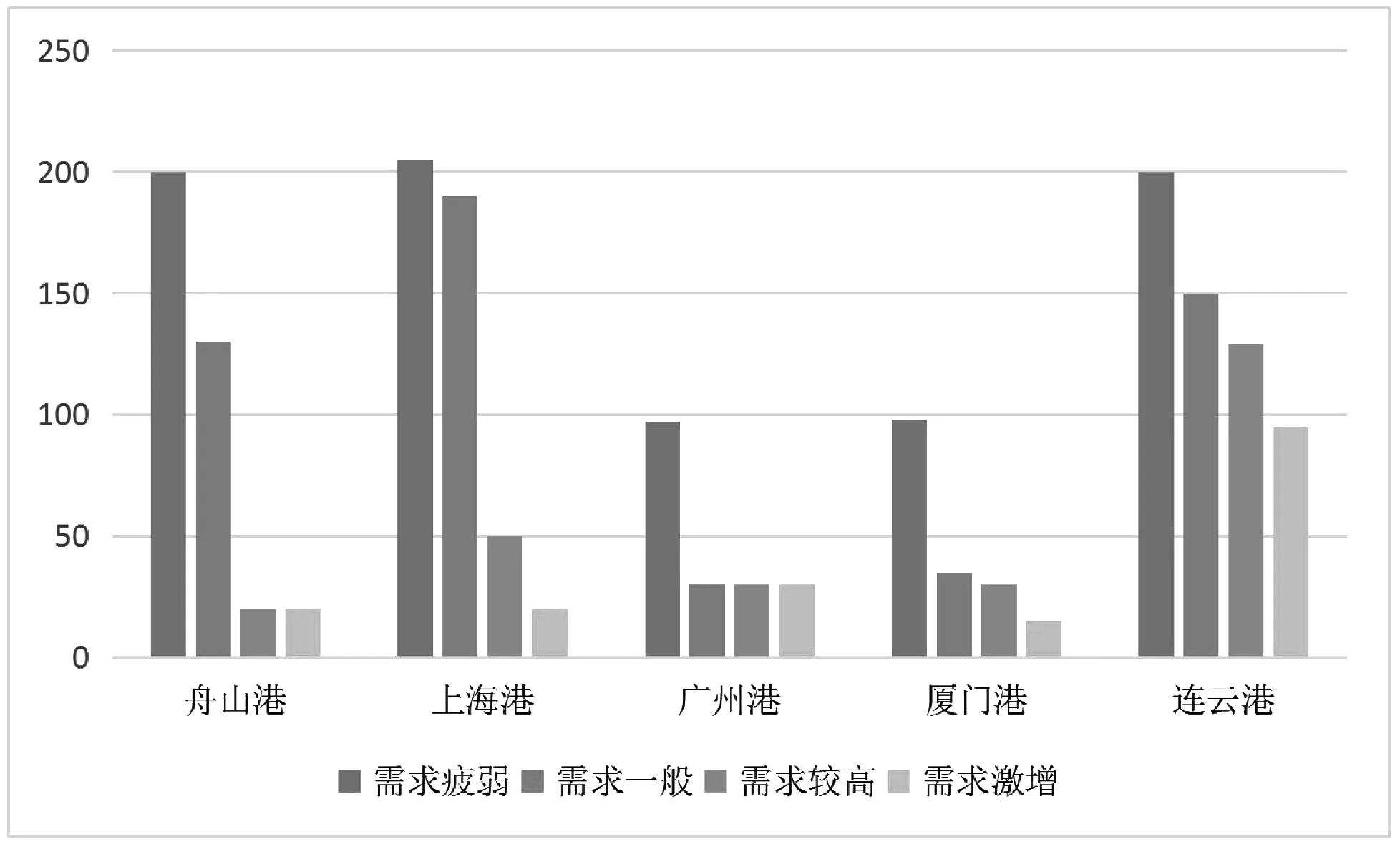
圖2 不確定情景下各港口庫存變化情況(單位：萬噸)

表3為不同情景下煤炭供應鏈的總費用運算結果，在消費地需求不斷增加的情況下，供應鏈的總費用也逐漸增加，“需求激增”情景比“需求一般”情景的供應鏈的總費用增加了近12%，因此，在需求不斷升高的情況下，需要及時補充庫存，避免煤價上漲以及缺貨懲罰帶來的高昂費用。圖1為不同情景下的鐵海聯運煤炭最優運輸路徑，企業在不同的需求情景下，考慮到運輸成本等，需要選擇不同的中轉港口進行中轉，而電廠選擇的目的港口相對固定，一般選擇庫存足夠且運輸費用較低的港口。在需求疲弱的情景下，包頭選擇秦皇島港進行中轉，需求上升時，選擇京唐港與天津港進行中轉；鄂爾多斯在需求不斷上升時，傾向于選擇秦皇島港進行中轉，中轉量也逐漸上升；神木在四種情景下都選擇天津港、青島港以及日照港進行中轉。

圖2為各港口庫存變化情況，在五個目的港中，連云港的煤炭庫存量下降相對較為緩慢，上海港與舟山港煤炭庫存量下降相對較快，可以看出隨著需求不斷升高，港口庫存量整體呈現下降的趨勢。需求一般與需求較高兩種情景下的港口庫存量差別最大，在目的港口中以上海港與舟山港最為顯著，因此在需求一般時，應及時補足庫存以抵御上漲的煤價和下游需求高漲的風險。

4 結論

本文根據煤炭供應鏈的結構，結合大型煤炭企業在鐵海聯運網絡中的運輸實例以及魯棒優化模型，設計了一個考慮不確定煤炭需求及煤炭價格的MIP模型，所構建的模型不僅將煤炭庫存限制作為約束條件，也將煤炭庫存成本放入目標函數中，建立利用IBM ILOG CPLEX Optimization Studio 12.6.0對案例中煤炭運輸的港口選擇、煤炭調配量、煤炭路徑及煤炭港口庫存進行求解，從而選擇合理的運輸—庫存方案。

本文未來的研究方向主要有兩個：

①提前期對于庫存的影響。在越來越多的行業中，基于時間的競爭日益重要，為了更好地實現煤炭成本和服務水平之間的優化，更好地管理庫存，需要從定量的角度進行分析提前期與煤炭庫存之間的管理問題。

②煤炭供需具有周期性，所涉及的數據數量龐大，需要開發一種更加便捷高效的算法求解大規模數據，將通過IBM ILOG CPLEX Optimization Studio 12.6.0計算的結果與新算法的計算結果進行比較，以驗證算法在求解該模型上的優越性。