指向數學核心素養的深度學習途徑探究

浙江省臨海市第六中學 (317000) 陳冬菊

在以提升學生數學核心素養為目標，以減輕學生學業負擔為愿景的新課程背景下，教師應努力提高課堂效率，培養學生分析問題和解決問題的能力，開展深度學習是實現這一目標的有效途徑．但筆者發現我們的課堂依然存在大量的淺表性學習和假性學習，那么，如何開展有效的深度學習？本文從四個方面進行闡述．

途徑一 開展一題多解進行深度學習

一個數學問題往往有多種解法，每種解法都可以開拓學生的思路，融會貫通．一題多解讓學生對問題進行多角度、多層次的深度學習，從中選擇快捷準確的最優解法，培養學生思維的全面性和靈活性，提升學生數學核心素養．

案例一 等差數列的前n項和Sn的最值問題

例1 (多選)已知遞減的等差數列的前n項和為Sn，若S7=S11，則( ).

A.a10>0 B.當n=9時，Sn最大

C.S17>0 D.S19>0

解法1：利用方程的思想可以把這個問題轉化為首項a1和公差d，這兩個基本量來解決．

圖1

途徑二 設計變式教學進行深度學習

變式教學是通過變換數學問題的非本質特征來暴露本質特征的教學方法．變式教學能促進學生數學思想方法的內化，能培養學生的創造性思維，能培養學生思維的深刻性，從而提升學生數學核心素養．

案例二 圓錐曲線的中點弦與點差法

在求解與圓錐曲線的中點弦有關的問題時，點差法是一種非常重要的方法，這種方法能較好體現解析幾何的設而不求思想，為了更好地深化這類問題，下面以橢圓為例設計變式教學．

圖2

這一性質看似簡單，但應用廣泛，高考試題經常涉及這一性質，值得深化學習，從而設計下面的變式進行深度學習．

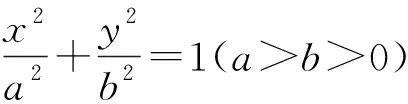
圖3

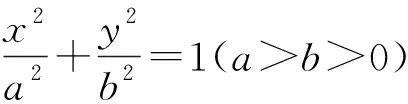
圖4

教師還可以對雙曲線設計類似上面的變式教學，另外，上面的問題都是針對焦點在x軸上的橢圓或雙曲線，我們還可以設計焦點在y軸上的橢圓或雙曲線的變式教學，問學生結論還會一樣嗎？通過這樣的變式開展圓錐曲線的中點弦問題的深度學習，效果比較好．

途徑三 制作微課進行深度學習

微課具有內容短小精悍、能重復使用、能激發學生學習興趣等特點，優勢明顯．實踐證明微課取得了實質性的教學效果．教師可利用微課這種新的教學手段針對某個知識點開展深度學習．

案例三 空間軌跡問題的求法

空間的軌跡問題圖形抽象，對學生的空間想象能力要求高，并且求解方法多樣，對學生來說是個難點．這時，可制作微課《空間軌跡問題的求法》開展深度學習，突破這一難點，學生興趣很高，教學效果良好．

例3 如圖5，在正方體ABCD-A1B1C1D1中，P是側面BB1C1C內一動點，若P到直線BC的距離與到直線C1D1的距離相等，則動點P的軌跡所在的曲線是( ).

圖5

A.直線 B.圓

C.雙曲線 D.拋物線

解析：在正方體中，易知直線C1D1⊥平面BB1C1C，∴C1D1⊥PC1，所以PC1就是點P到直線C1D1的距離，那么，點P到直線BC的距離等于它到點C1的距離，根據拋物線的定義，點P的軌跡是拋物線，故選D．本題利用拋物線的定義得出所求軌跡的形狀，這是求解空間軌跡問題的第一種方法——定義法．

例4 如圖6，平面α的斜線AB交平面α于點B，且與平面α成60°，平面α內一動點C滿足∠BAC=30°，則動點C的軌跡所在的曲線是( ).

圖6

A.直線 B.圓

C.橢圓 D.雙曲線的一支

解析：∵∠BAC=30°，所以直線AC繞著軸AB旋轉形成的圖形是圓錐的側面，又因為動點C在平面α內，所以，原問題相當于用一個與軸成60°的平面去截圓錐的側面，那么得到的軌跡是橢圓，如圖7所示．故選C．本題利用不垂直于軸的平面截圓錐截口曲線的形狀的結論得出答案，這是求解空間軌跡問題的第二種方法——幾何法．

圖7

例5 如圖8，已知正方體ABCD-A1B1C1D1的棱長為1，點P是平面ABCD上的動點，若點P到直線A1D1的距離等于點P到直線CD的距離，則動點P的軌跡所在的曲線是( ).

圖8

A.拋物線 B.雙曲線

C.橢圓 D.直線

利用以上三個例題制作的微課內容精簡，主題突出，能使學生較好地掌握空間軌跡問題的三種典型求法：定義法、幾何法和代數法．

途徑四 組織小組合作學習進行深度學習

小組合作學習可以提升課堂的活躍程度，能引發學生的深層思考，能培養學生的主動參與意識．小組合作學習形成了師生、生生之間的全方位、多層次、多角度的交流模式，是進行深度學習的一種重要方式．

案例四 四點共面問題

圖9