一道變系數胡不歸問題詳探

廈門大學附屬實驗中學 (363123) 楊 坤 林運來

1 試題呈現

在如圖1所示的Rt△ABC中,∠C=90°，∠A=30°，BC=5，P為AC上一動點,則2BP+AP的最小值為.

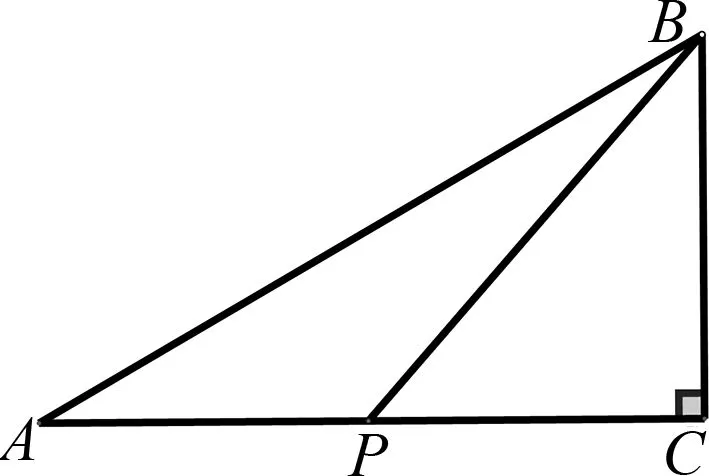
圖1

本題是典型的胡不歸問題,題雖小,意且長. 出自先秦佚名的《國風·邶風·式微》的胡不歸問題,由于其較強的文學性和源遠流長的數學文化日益成為中學數學考試中的熱點難點問題.筆者查閱資料發現,長久以來關于胡不歸問題的解法相對單一(解法1),且僅僅局限于幾何構造,較少代數解法.隨著學生數學學習的不斷深入,解法應該逐步多樣.基于維果斯基的最近發展區理論,解題教學也要基于學生的現有發展水平,為此根據學生的不同學習階段,筆者依次提供以下解法:

2 解法探究

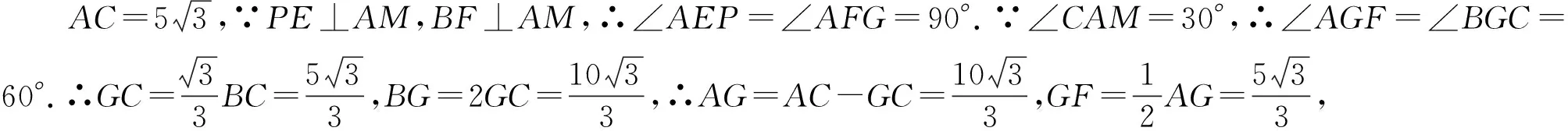
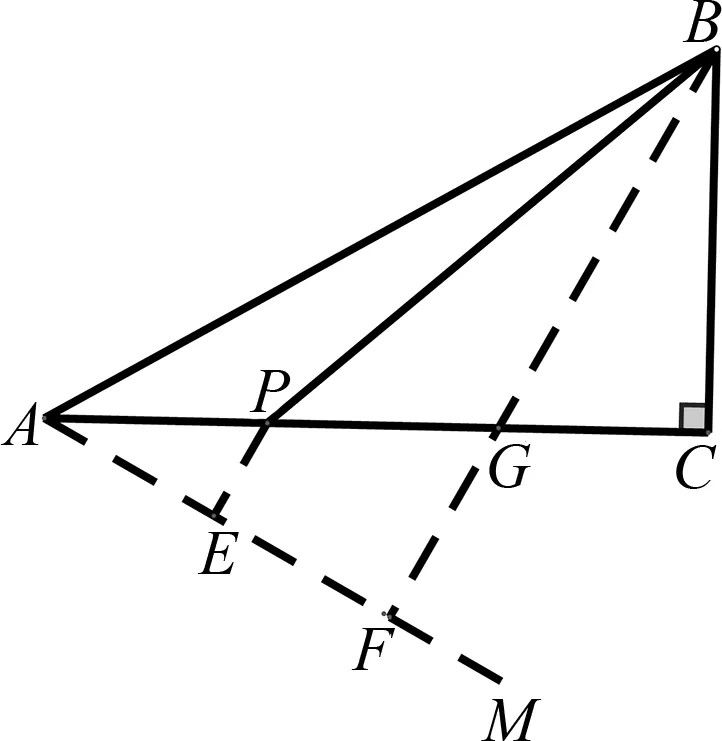
圖2

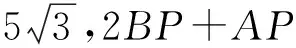
評注：解法1是胡不歸類型的典型解法,在初中學完直角三角形即可應用.但學生初次接觸時極難想到提系數,只有經過啟發練習后才能初步掌握.

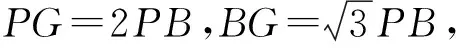
圖3

評注：解法2學完相似三角形即可應用,但此法是非典型的線段構造,強調的是動點的軌跡(軌跡方程).

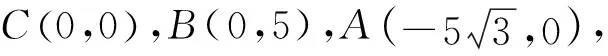
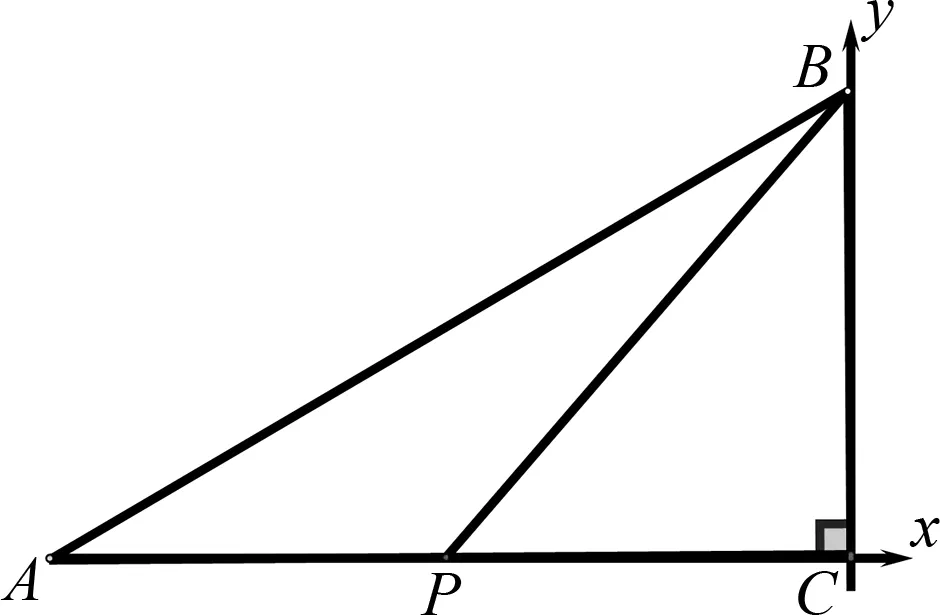
圖4

評注：解法3在學完一元二次方程即可應用,但是要求較高的數學抽象能力和極好的數學運算能力.

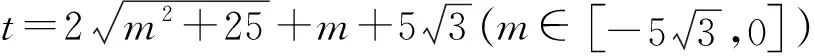
評注：解法4在學習完三角函數即可應用,但由于對此種問題的三角換元望而卻步,實際教學效果一般.

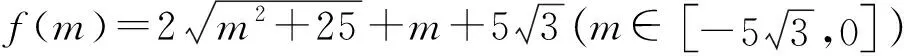
評注：解法5在學習完導數后即可應用,但高中生雖然會導數求最值,卻對根式求導不敢輕易嘗試.

3 解后反思

根據維果斯基最近發展區理論,解題教學一定要掌握學生目前的發展水平,進而設置與之相當的題目,激發其興趣,利用其潛能,從而超越其最近發展區而達到下一階段的發展水平，然后在此基礎上進行下一個發展區的發展.為完成此目標,示范、引導和激勵學生掌握多種不同階段和層次的解法,以及各種解法之間的對比也是尤為必要的.當然,本文中的幾種解法并未窮盡所有解法思路.但是,這些不同的解法涉及到許多的解題思路,運用了不少知識點,解題教學中多進行此種小題的解題思維訓練,能有助于進一步減輕學生的學習負擔,提高學生的邏輯思維水平,從而達到提升學生的創新精神和探索能力.