通過一道試題研究與拋物線切線相關的性質

廣東省佛山市順德區李偉強職業技術學校 (528300) 王曉敏

拋物線具有豐富的幾何性質，如果在解題的過程中能靈活地運用相關性質，那么在解題的過程中就可以起到事半功倍的效果.筆者在研究一道拋物線相關問題時，就從中總結了多條相關性質，并發現其中隱含了一個“阿基米德三角形”.

一、題目及分析

如圖1，過點Q(-2,m)作拋物線y2=8x的兩條切線，切點分別為A，B，直線QA，QB分別交y軸于C，D兩點，若S△QAB=6S△QCD，求m的值.

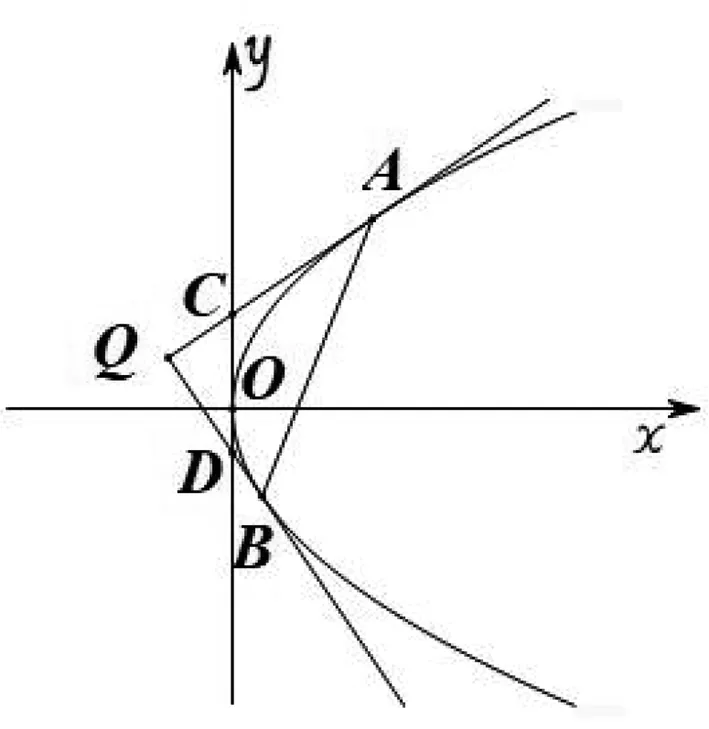
圖1

分析：觀察可知，點Q位于拋物線的準線，過該點作拋物線切線所構成的切點弦[1]必經過拋物線的焦點.為此，我們可以利用焦點弦這一信息來計算△QAB的面積.為了計算△QCD的面積，還需考慮點C，D所滿足的幾何關系.

二、解法呈現

為了解決上述問題，現將解題過程分解為如下幾個環節.

環節一：切點弦AB過焦點F

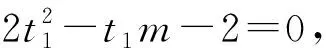
解法二：(以極點極線[2]的意義求解)根據極點極線的幾何意義可得以點Q為極點，對應的極線為切點弦所在的直線，即直線AB.根據極點極線的代數意義可得，當點Q的坐標為(-2,m)時，其關于拋物線y2=8x的極線方程為AB:my=4(x-2)，即可得該方程恒過拋物線的焦點(2,0).

環節二：計算△QAB的面積

根據上述證明過程可知直線AB恒過焦點(2,0)，可設直線方程為AB:x=ty+2.設該直線對應的極點為T(x0,y0)，利用極點極線的代數意義可得直線AB的方程應為AB:y0y=4(x+x0).根據兩直線方程相同，可得x0=-2，y0=4t，結合點Q的坐標可得m=4t.

說明：該表達的意義在于以直線AB為基本量，能極大地簡化后續的運算以及證明.

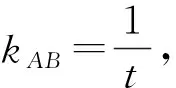
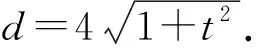
環節三：關于點C，D的幾何性質

如圖2，分別過點A，B，F作準線l的垂線，垂足為M，N，F′.根據拋物線的光學性質，切線QA為∠MAF的角平分線，易知△MAF為等腰三角形，故直線QA經過MF的中點.考慮△MFF′，MF與y軸的交點即為MF的中點.綜上可得：QA與y軸的交點C為MF的中點.同理，QB與y軸的交點D為NF的中點(證明過程詳見后文).

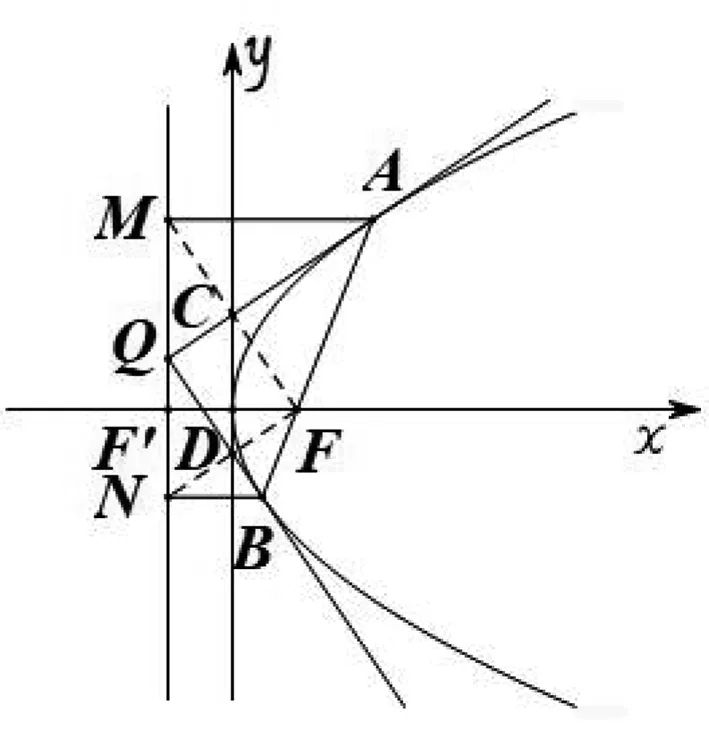
圖2

在直角梯形AMNB中，可得∠MAB+∠NBA=180°，從而AQ⊥BQ，即四邊形QDFC為矩形.

環節四：計算△QCD的面積

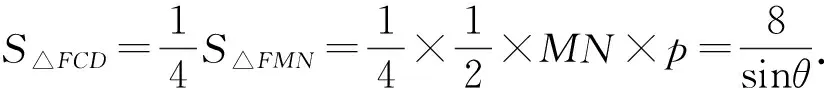
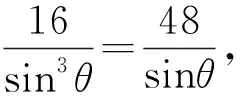
三、總結試題所蘊含的一般性質

在上述解題過程中，出現了很多與拋物線相關的幾何性質，現對出現的性質進行梳理.

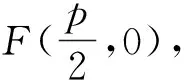
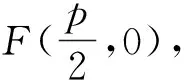
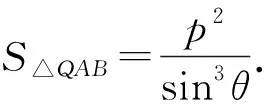
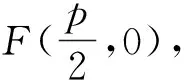
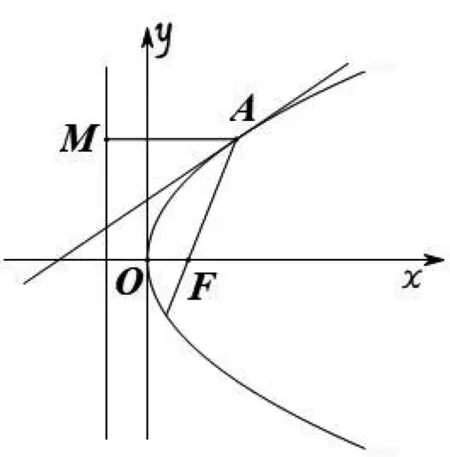
圖3

性質3 如圖4，已知拋物線y2=2px(p>0)，分別過點A，作準線l的垂線，垂足為M，N，過點A，B作拋物線的切線lA，lB交于點Q，則有AQ⊥BQ，即四邊形QDFC為矩形.

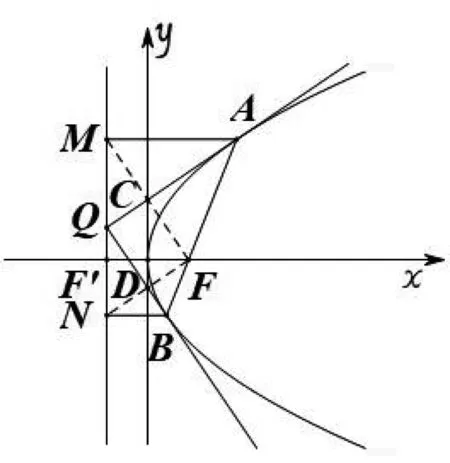
圖4

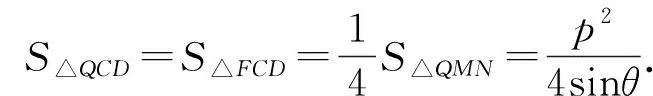
只要將上述證明過程中的問題進行一般化處理即可得到上述性質的證明，本文不再贅述，現僅介紹一下性質2的證明過程.

關于光學性質的證明，可以通過角平分線的性質以及切線的極限定義進行幾何方面的證明，也可利用代數方程進行證明.本文僅介紹第二種證明思路.

證明：如圖5，設點A的坐標為(x1,y1)，根據極點極線的結論過點A的切線方程為lA:y1y=p(x+x1).該直線與x軸的交點為T(0,-x1)，結合拋物線的定義可得TF=AF，即可得△ATF為等腰三角形，從而即可得切線l為∠MAF的角平分線.

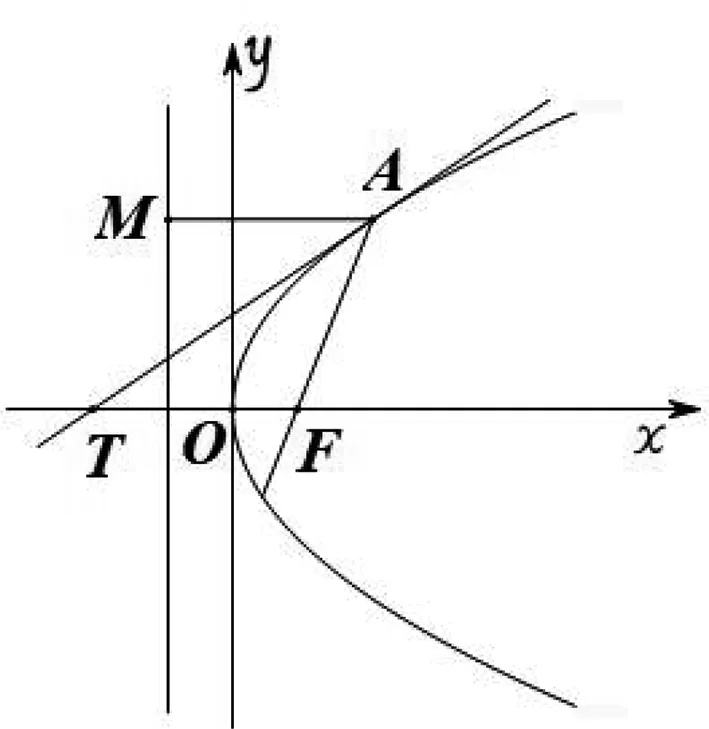
圖5