圓錐曲線的兩個(gè)共同性質(zhì)

江蘇省東海高級(jí)中學(xué) (222300) 孫通喜

結(jié)論一已知曲線C：mx2+ny2=1以及一點(diǎn)P(x0,y0)(P點(diǎn)不在曲線C上)，過(guò)P點(diǎn)作兩條斜率互為相反數(shù)的直線l1，l2，分別交曲線C與A、B、C、D，則有PA·PB=PC·PD.

結(jié)論二已知拋物線C：y2=2px(p>0)及點(diǎn)P(x0,y0)(P點(diǎn)不在曲線C上)，過(guò)P點(diǎn)作兩條斜率互為相反數(shù)的直線l1，l2，分別交C與A，B，C，D，則PA·PB=PC·PD.

綜上，我們有:

定理一過(guò)平面內(nèi)一點(diǎn)P作兩條斜率互為相反數(shù)的直線l1，l2，分別與圓錐曲線交于不同的兩點(diǎn)A,B,C,D，則有PA·PB=PC·PD.

圖1

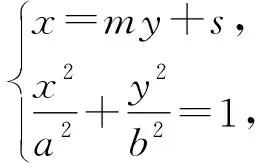
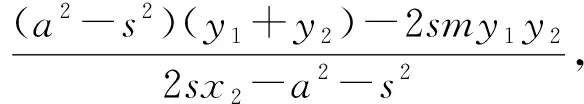
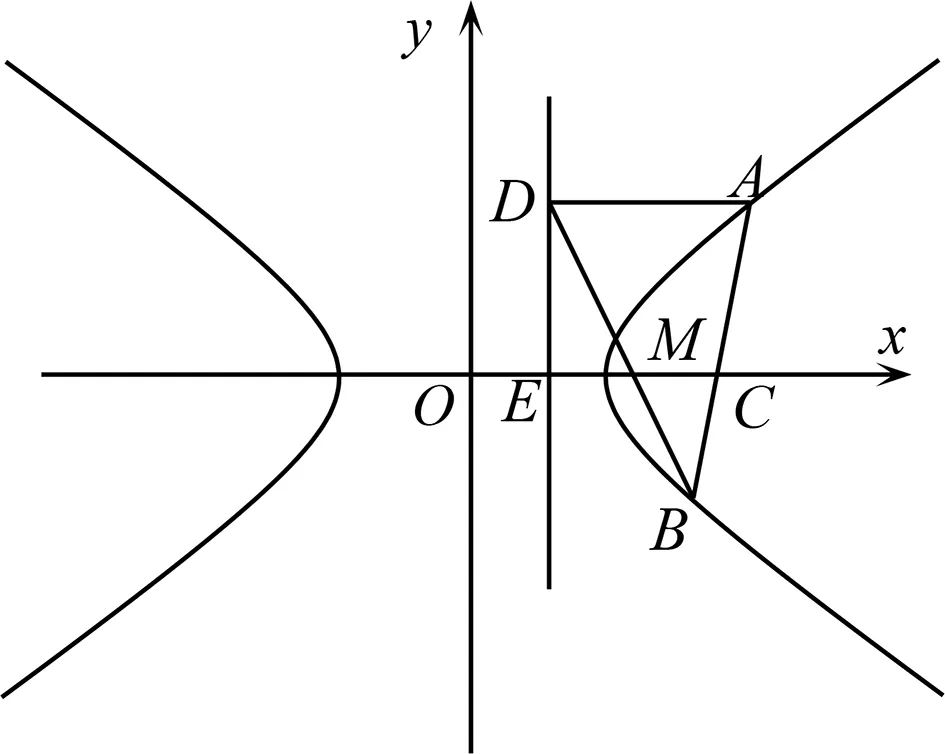
圖2

證明同結(jié)論三，讀者可以自行證明.

綜上，我們有：

上述結(jié)論對(duì)于拋物線也有相同的結(jié)論，讀者不妨自己試試.