一道2022屆高三調研試題的探究

福建省仙游華僑中學 (351200) 薛玉榮

本題的答案是：(1)拋物線C的方程為y2=4x；(2)直線TM與拋物線C相切.第(2)問內涵豐富，不應解完即止，可進一步引導學生進行適當的探究.

1.縱向探究——一般性結論

本題(2)的結論是關于拋物線C：y2=4x，那么，對于一般的拋物線C：y2=2px(p>0)，原結論是否成立？經探究，可得：

2.逆向探究——結論的逆命題

3.變式探究——新的結論

上述結論涉及拋物線C的經過頂點O的弦OM，那么，對于拋物線C的任意弦AM,會有什么相應的結論？經探究，可得：

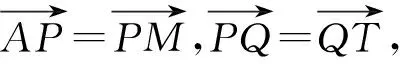
證明：下面只證明拋物線C：y2=2px(p>0)的情形.設直線AM的方程為x=hy+m，代入拋物線C的方程，并整理得y2-2phy-2pm=0.設A(x1,y1),M(x2,y2),據韋達定理得y1+y2=2ph.

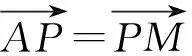
進一步探究，還可以得到：

特別地，當2p=1,n=c時，結論5中關于拋物線C：x2=2py(p>0)的結論，就是2007年全國高考江蘇卷題19(2)、(3)的結論：在平面直角坐標系xOy中，過y軸正方向上一點C(0,c)任作一直線，與拋物線y=x2相交于A、B兩點，一條垂直于x軸的直線，分別與線段AB和直線l：y=-c交于P，Q.(1)略；(2)若P為線段AB的中點，求證QA為此拋物線的切線；(3)試問(2)的逆命題是否成立？說明理由.(圖略)

以上通過對一道拋物線試題的探究，揭示了試題的深刻背景及一般規律和結論，并應用所得到的結論解決有關問題.這對培養學生發現、提出、解決問題的能力，提升學生的探究能力和數學學科核心素養無疑是有益的.