運用偶函數性質優化解題

安徽省宿城第一中學 (234000) 陳玉龍

函數的奇偶性是函數的一個重要性質，本文通過典型實例的分析剖解，介紹偶函數幾種性質特點的應用，旨在強化對偶函數性質的理解，提升所學知識的運用能力，供同行們參考.

一、關注偶函數的定義域

例1 已知二次函數f(x)=ax2+bx+c是定義在[a-1,,2a]上的偶函數，求此函數的單調增區間.

解析：由于f(x)是偶函數，則其定義域應關于原點對稱，即有1-a=-2a，則，所以f(x)=-x2+bx+c，又由偶函數的定義得，在定義域內都有f(-x)=f(x)得-bx=bx成立，即有b=0，故f(x)=-x2+c，所以函數f(x)的單調增區間為(-∞,0].

評注：函數的定義域關于原點對稱是函數為“奇函數和偶函數”的必要條件，此條件比較容被忽視，必須進行強化.

例2 已知函數f(x)是偶函數，且在(0，+∞)上單調遞增，若f(-1)=0，試求關于x的不等式xf(x)<0的解集.

圖1

評注：考慮到偶函數的定義域關于原點對稱，則由給出的部分單調區間可推出整個函數的定義域和單調性，再抓住特殊點，就能夠勾畫出函數的大致圖像，這樣成功解題就是比較容易的事了.

二、關注f(-x)=f(x)的應用

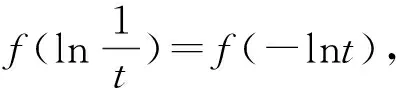
評注：由f(-x)=f(x)一般常用來判斷一個函數是否是偶函數，而本例中反用此性質化簡所給的不等式，從而顯露出解決的機會.

例4 設a為非零實數，偶函數f(x)=x2+a|x-m|+1(x∈R)在區間(2,3)上存在唯一的零點，求實數a的取值范圍.

評注：根據偶函數的性質解決了所給表達式中的參數，為下一步的解題掃清了障礙，這是成功解題的重要一環.

三、關注偶函數圖象關于y軸對稱

例5 若f(x)是R上的偶函數,且滿足f(x+2)=f(x)，當x∈[0,1]時,f(x)=2x.若在區間[-2,3]上方程ax+2a-f(x)=0恰有四個不相等的實數根，求實數a的取值范圍.

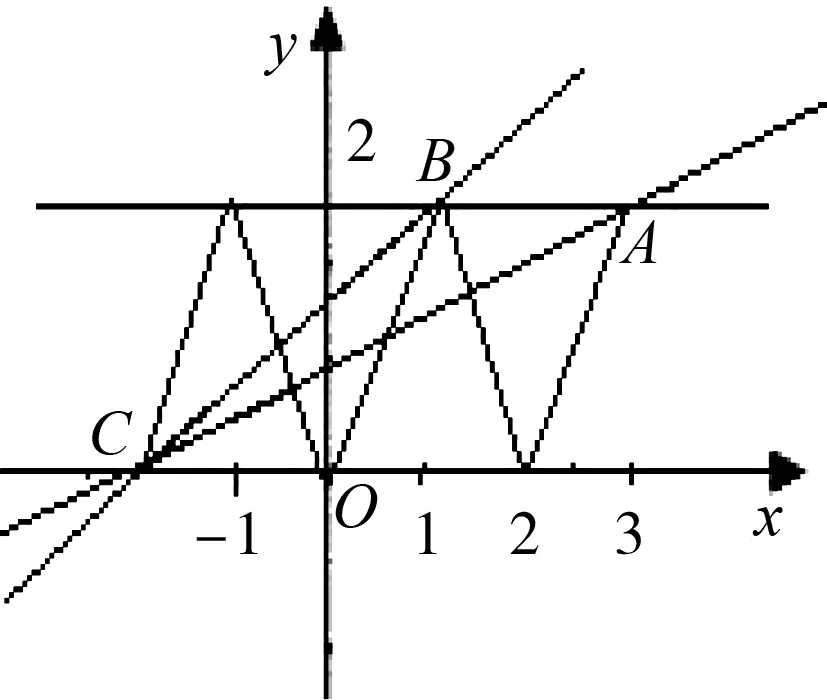
圖2

評注：偶函數的圖像關于y軸對稱是函數的重要幾何性質，在涉及畫圖像時必須關注幾何性質的運用，本題中，根據此性質畫出整個函數圖像是解題的成功的關鍵.

例6 定義在R上的函數在(-∞,a]上是增函數，函數y=f(x+a)是偶函數，當x1a，且|x1-a|<|x2-a|時，試判斷f(2a-x1)與f(x2)的大小關系.

解析：由于函數y=f(x+a)是由y=f(x)向左平移a個單位所得，而y=f(x+a)是偶函數，所以y=f(x)的函數圖像關于x=a對稱.又在(-∞,a]上是增函數，故在(a,+∞)是減函數，當x1a，且|x1-a|<|x2-a|時，去掉絕對值符號得a-x1a，x2>a，由在(a,+∞)是減函數得f(2a-x1)>f(x2).

評注：通過研究給出的偶函數條件，判斷出函數y=f(x)的圖像的對稱性，這是判斷兩個函數值大小的關鍵舉措，此處顯示了圖像性質的對于解題的重要性.

四、關于f(x)=f(|x|)的應用

點評：通過判斷出函數的單調性與奇偶性后，就將一個隱含關系轉化為一個簡單的絕對值不等式，充分發揮了隱含的偶函數條件的解題作用.

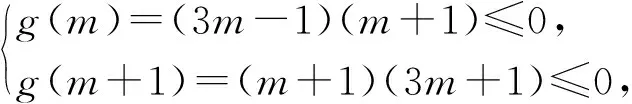
評注：這里通過運用f(x)=f(|x|)和函數的單調性，將待求的函數不等式轉化為絕對值不等式，成功地避免了分類討論所引起的不方便.

在我們的解題教學中，要幫助學生挖掘一些概念和性質的用途，尤其是如何運用它們去優化解題，通過在我們的課堂上示范和歸納，可以起到率先垂范、畫龍點睛的作用.