一個面積恒等式及其應(yīng)用

江蘇省無錫市第六高級中學(xué) (214023) 謝 吉

三角形塞瓦線背景下有很多有趣的結(jié)論.筆者在學(xué)習(xí)、研究的過程中，關(guān)注到一個面積恒等式，利用該面積恒等式簡捷地證明或解答了一組幾何競賽題，為一類幾何競賽題增添了一道亮麗的風(fēng)景線.

命題如圖1所示，點P是△ABC內(nèi)一點，直線AP,BP,CP分別交線段BC,CA,AB于點D,E,F，記S△BPD=x，S△CPD=u，S△CPE=y，S△APE=v，S△APF=z，S△BPF=w，則xyz=uvw.

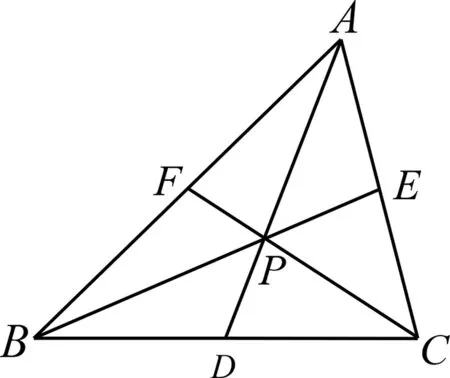
圖1

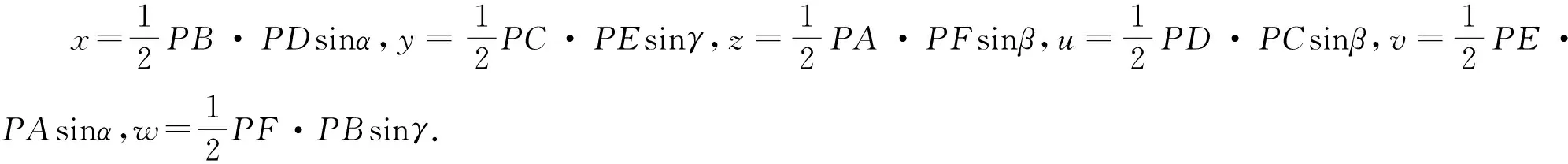
就圖形特征來說，塞瓦線型幾何競賽題的線段比例關(guān)系，均可轉(zhuǎn)化為面積的比例關(guān)系，把相關(guān)幾何元素用x、y、z、u、v、w(或比例)表示出來，這樣，在處理問題時，顯得十分靈活、簡便.

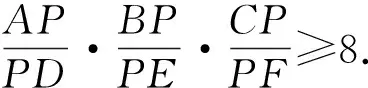
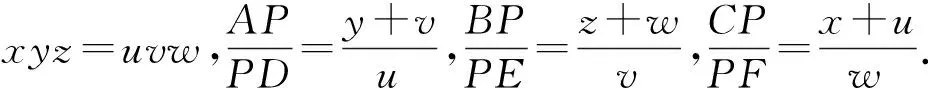
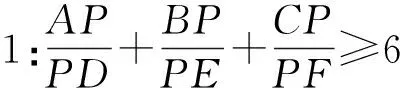
例2 (第32屆IMO試題)如圖2所示，設(shè)P是△ABC內(nèi)的一點，求證：∠PAB、∠PBC、∠PCA至少有一個小于或等于30°.

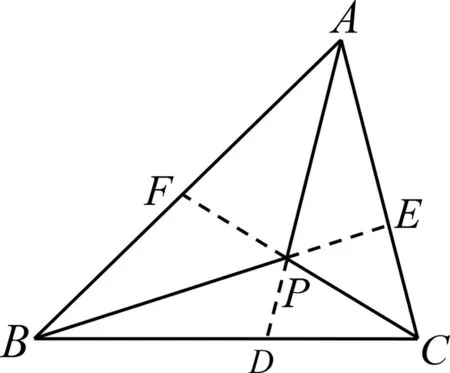
圖2

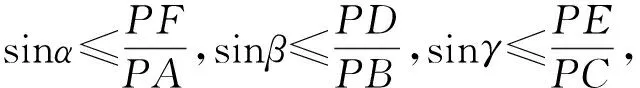
例3 (第37屆IMO預(yù)選題)如圖3所示，設(shè)△ABC是銳角三角形，外接圓圓心為P，半徑為R，AP交BPC所在的圓于另一點A′，BP交CPA所在的圓于另一點B′，CP交APB所在的圓于另一點C′，證明：PA′·PB′·PC′≥8R3，并指出在什么情況下等號成立？

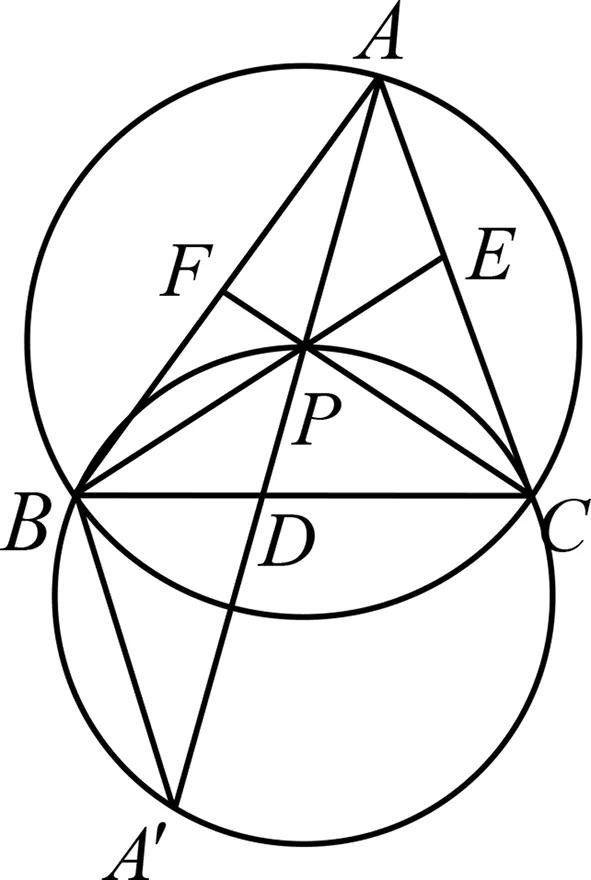
圖3

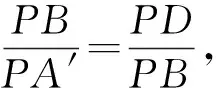
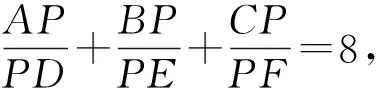
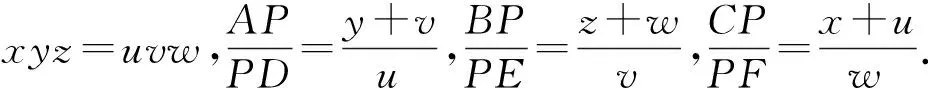
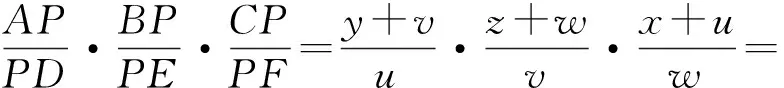
例5 (2012年第24屆亞太數(shù)學(xué)(APMO)競賽試題) 如圖4所示，已知P為△ABC內(nèi)部的一點，且D、E、F分別為直線AP與邊BC，直線BP與邊CA，直線CP與邊AB的交點.如果△PFA，△PDB與△PEC的面積為1，試證明：△ABC的面積為6.

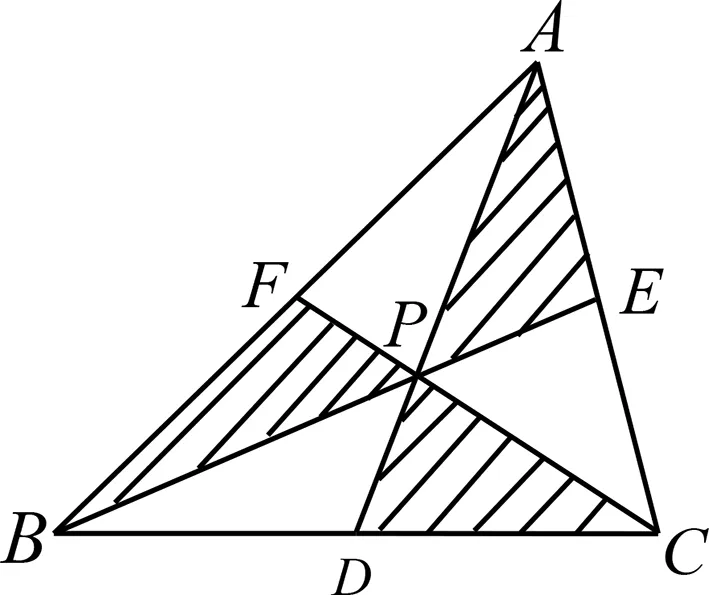
圖4

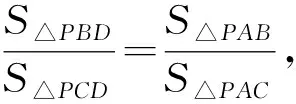
幾何競賽題的求解歷來是難點，尤其是幾何不等式的證明.學(xué)習(xí)的過程中，追求自然而平凡的證明一直是筆者的追求.在這個基本圖形中，是否還有其他的面積關(guān)系？留給讀者思考.