常數和變化積雪密度方案診斷計算積雪厚度的敏感性研究

張慧敏 ，金梅兵 ，祁第

(1.南京信息工程大學 海洋科學學院，江蘇 南京 210044；2.南方海洋科學與工程廣東省實驗室（珠海），廣東 珠海 519080；3.自然資源部第三海洋研究所 自然資源部海洋大氣化學與全球變化重點實驗室，福建 廈門 361005；4.集美大學極地與海洋研究院，福建 廈門 361021)

1 引言

海冰上的積雪是極地氣候的重要組成部分，影響著海洋與大氣間的能量平衡和水分交換。雪與海冰的物理性質存在差異，比如雪的反照率高于海冰，雪對光的衰減作用遠大于海冰[1]，雪還是短波輻射平衡過程中的重要因素，影響著海冰的生長、消融[2]。雪的密度影響其熱導率[3]，進而影響海冰與大氣間的熱交換。海冰上的積雪相當于一個保溫層，當積雪厚度較大時，隔熱效果較好。

密度是雪的基本物理性質之一，會受到降雪期間的氣象要素影響。當氣溫遠低于冰點時，雪密度通常較低，在可發生降雪的條件下，雪密度與氣溫大致呈明顯正相關[4]。在雪降落到地面后停留的這段時間內，積雪密度可能在風力作用下增大[4]。雪密度值存在一定的變化范圍，為50～550 kg/m3[5-10]。以往對積雪的研究大部分在陸地區域，根據雪的密度受到氣溫、風速等因素的影響，前人擬合了一些計算雪密度的經驗公式[6,11-16]。例如，由Hedstrom 和Pomeroy[11]擬合的雪密度隨氣溫變化的經驗公式曾被Bartlett 等[14]應用于CLASS（Canadian Land Surface Scheme）3.1 版本，也被Lundberg 和Feiccabrino[17]用于估算雪密度。Avanzi 等[18]基于不同的雪密度經驗回歸模型研究美國西部地區積雪厚度與降水量之間的關系，但大多數經驗回歸模型將雪深視為雪密度的唯一預測因子，導致無法重現觀測的雪厚與雪水當量的關系，使得觀測和估計的積雪密度變化在冬季中期一致性高、春季一致性低。有學者認為，新雪密度可能與雪粒大小、類型有關，后來還有學者對新雪的密度變化及其與氣溫等要素之間的關系進行了研究[19]。此外，氣旋活動是北極降雪的重要影響因子，研究表明，氣旋引起的大西洋地區降雪占該地區總降雪量的80%，而引起太平洋地區降雪占該地區總降雪量的50%左右[20]。

積雪的參數設置影響海冰模式的模擬效果[21-22]。如積雪密度值影響積雪厚度，進而影響雪的透光性等物理特性。海冰模式從發展初期側重于海冰熱力學部分[23]發展到動力學、熱力學與海冰厚度分布等多組成部分[24]。積雪的變化除了對海冰模式的相關參數敏感外，還與雪齡有關，如多年冰上的雪齡比一年冰上的更長[10]。北極海冰面積及多年冰面積在近幾十年里迅速減小，且減小的速率還在不斷加快[25-26]。

隨著對兩極積雪變化的關注度增加，不同學者提出了對極地積雪密度、厚度變化的不同模擬方案[10,27-29]。如De Michele 等[27]使用多元回歸方法估算積雪密度，并認為積雪可分為干雪和濕雪，分別計算各部分雪的質量后再計算整體的雪密度。這體現了積雪在部分融化時雪密度增大的特征。此外，有研究人員開發了海冰上基于歐拉方法或拉格朗日方法預報積雪密度和厚度的模型。如Petty 等[29]開發了用于估計雪厚度、密度的NESOSIM（NASA Eulerian Snow on Sea Ice Model）模式。NESOSIM 是一個三維的兩層雪模式（上層新雪、下層舊雪），組成該模式的幾個參數化過程代表了積雪期內積雪變化的關鍵機制[29]。NESOSIM 還考慮了新雪可能在風力作用下移動到冰間水道造成雪量損失的情況。還有，Liston 等[10]開發了用于研究北極地區海冰上積雪變化的SnowModel-LG（Lagrangian Snow-Evolution Model）模式。該模式考慮了氣溫、風、濕度等氣象要素以及吹雪升華等過程對雪密度的影響[30]。Blanchard-Wrigglesworth 等[28]利用降雪數據、海冰運動和歐洲中期天氣預報中心提供的再分析降雪量數據（ERA-Interim），基于拉格朗日方法的模式模擬海冰上的積雪厚度，模擬結果與冰橋計劃（Operation IceBridge,OIB）、冰質量平衡浮標（Ice Mass-balance Buoys,IMBs）的實測數據存在差異，他們將這一差異歸因于未考慮升華或風力作用等因素導致了雪厚變化。再加上高緯度地區降水率的不確定性[31-32]，因此，有待開發出應用于海冰模式的積雪密度參數化方案，以提高對極地區域氣候的模擬能力，更好地理解積雪變化對極地以及全球氣候變化的影響。目前的大多數氣候模式仍采用常數雪密度，這一做法雖降低了降雪不確定性導致的積雪密度誤差[33]，但同時也忽略了積雪密度隨升華、壓實、氣溫和風速等因子變化的細節。尹豪等[34]考慮的積雪變化的物理過程則更為合理，將積雪分為新、舊兩個雪層，并加入各雪層的密實化過程對積雪厚度的影響，能較好地再現積雪厚度的變化。但氣象要素對積雪密實化過程的相對重要性有待探究。本文先對比北極圈內積雪厚度的觀測和模式結果，再用單點的積雪厚度長時間觀測序列檢驗不同雪密度方案診斷計算的積雪厚度，分析不同氣象要素對雪密度的影響以及變化雪密度對雪厚度模擬結果的短期與長期影響。

2 數據和方法

2.1 模式數據

2.1.1 氣候模式數據

這里選取兩個積雪密度參數取常數（330 kg/m3）的氣候模式的雪厚模擬結果進行分析。第六次國際耦合模式比較計劃（the Sixth Coupled Model Intercomparison Project,CMIP6）中CESM2（Community Earth System Model version 2）與南京信息工程大學地球系統模式（NUIST Earth System Model version 3,NESM3）分別是由美國國家大氣研究中心與中國南京信息工程大學發布的地球系統氣候模式，均提供了對地球過去、現在和未來氣候狀態的模擬。二者都包含大氣、海洋、陸地和海冰4 個分量，不同的是，CESM2 還加入了海洋生物化學、氣溶膠、大氣化學和陸地冰4 個分量。以海冰分量為例（表1），CESM2 使用美國Los Alamos 國家實驗室開發的CICE 海冰模式5.1 版本；NESM3 則使用了該模式的4.1 版本，并改進了冰雪的反照率的精度[35]。Wang 等[36]評估了不同版本CICE海冰模式模擬北極海冰時空分布特征的能力，CICE 6.0 解決了CICE 4.0 和CICE 5.0 低估多年冰變化趨勢、高估季節冰變化趨勢等問題。但CICE 海冰模式的積雪密度仍取為常數[37]。本文采用CESM2 和NESM3在溫室氣體排放中等強迫情景（SSP245，即對RCP4.5情景的升級）下模擬的北極地區2015 年10 月至2018 年7 月3 年的月平均積雪厚度，與SnowModel-LG 模擬的對應時段結果作對比。

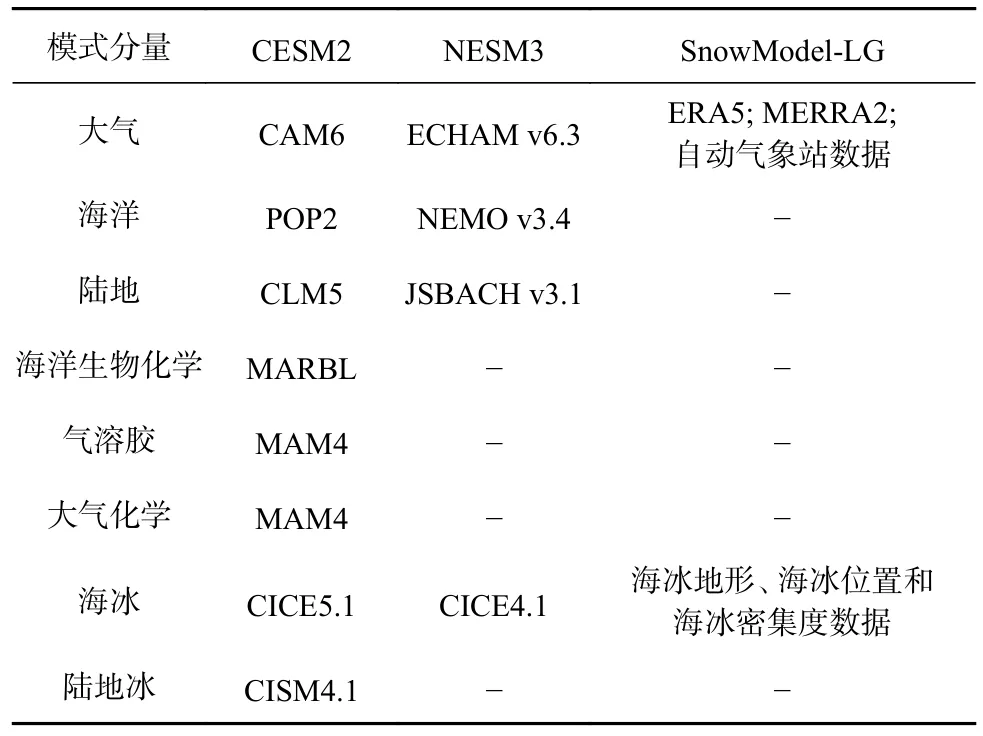
表1 CESM2、NESM3 和SnowModel-LG 的分量模式比較Table 1 Comparison of component models among CESM2,NESM3 and SnowModel-LG

2.1.2 SnowModel-LG 數據

本研究選取Stroeve 等[30]用SnowModel-LG 模式模擬的北極圈內2015 年10 月至2018 年7 月的積雪厚度數據（http://dx.doi.org/10.5067/27A0P5M6LZBI）。SnowModel-LG 是由Liston 等[10]和Stroeve 等[30]開發的基于拉格朗日方法模擬北極地區1980 年8 月至2018 年7 月積雪厚度和密度變化的模式。該模式包括能量平衡（EnBal）、積雪分層（SnowPack-ML）、吹雪過程（SnowTran-3D）、雪床生成（Snow Dunes）和數據同化過程（SnowAsim）5 個模塊[10]，專注于研究模擬積雪的生長、消融等變化。

2.1.3 ERA5 再分析資料

10 m 水平風場、2 m 露點溫度、2 m 氣溫、平均海表面氣壓、平均表面向下長波輻射、平均表面向下短波輻射、降水量等逐3 h 大氣強迫場數據來自歐洲中期天氣預報中心第五代再分析資料（the Fifth Generation ECMWF Reanalysis,ERA5），空間分辨率為0.25°×0.25°。經過空間插值與日平均處理后得到近海SNOTEL 測站普拉德霍灣（Prudhoe Bay,PB）站（圖1）逐日的氣象要素數據，用于驅動PB 站積雪厚度模擬的模式。

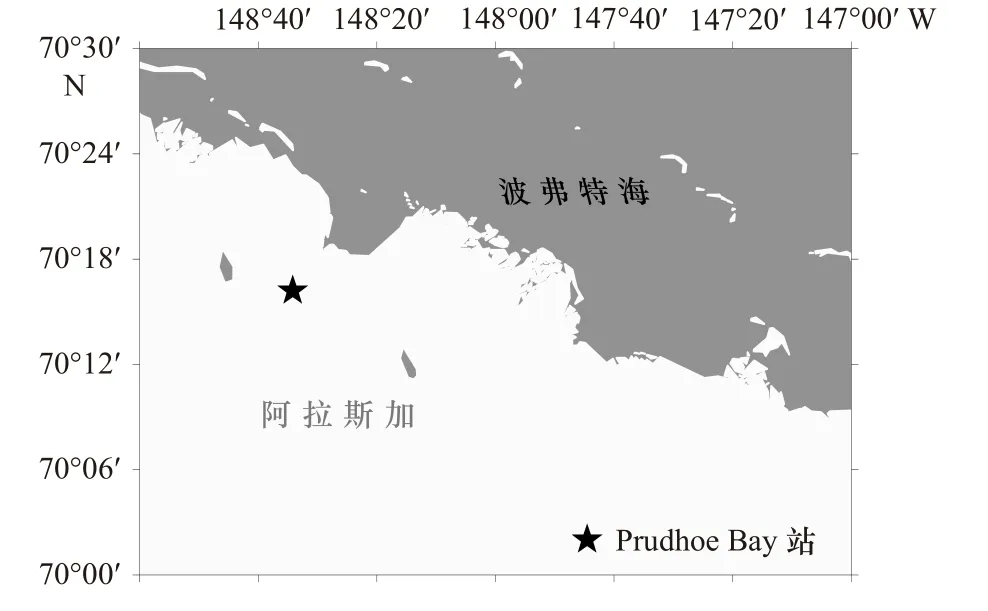
圖1 普拉德霍灣站的地理位置Fig.1 Location of Prudhoe Bay Station

2.2 實測數據

2.2.1 CryoSat-2 衛星遙感積雪厚度

CryoSat-2 衛星由歐洲航天局建造，用于確定地球大陸冰蓋和海洋冰蓋厚度的變化以及檢驗全球變暖導致北極冰層變薄的預測（http://www.altimetry.info/missions/current-missions/cryosat-2/）。該衛星運行時間始于2010 年4 月，攜帶1 個SIRAL 高度計和1 個DORIS儀器，其觀測的數據為2010-2020 年期間每年10 月至翌年4 月的極地積雪厚度（http://data.meereisportal.de/）。本研究選取CryoSat-2 衛星觀測的2015-2017年每年10 月至翌年4 月積雪厚度數據，用于檢驗CESM2、NESM3 與SnowModel-LG 模擬的結果。

2.2.2 SNOTEL 測站數據

1 9 7 9年2月1 7日，中國人民解放軍在云南、廣西兩線對越南軍隊展開全面反擊，戰線迅速推至越南境內。來自湖南的2 3歲偵察兵馮仁昌，此刻作為東線（廣西方向）先頭部隊，開始進攻中越邊境線上—個高不足百米的山頭——庭毫山。

為研究變化雪密度與常數雪密度對雪厚度的影響，本研究采用近海的SNOTEL 測站PB 站（70.27°N,148.57°W，圖1）2011-2019 年逐日的積雪厚度觀測數據，包括逐日最高氣溫、最低氣溫、降水量和積雪厚度數據。其中，積雪厚度通過激光測距的雪厚傳感器測量，其誤差原因主要是由于雪表面存在空氣孔隙而引起的光束反射不一致。這里將敏感性實驗結果與該時段觀測的PB 站積雪厚度進行直觀比較，再從均方根誤差、相關性等角度分析。

2.3 變化的積雪密度方案

這里采用Liston 等[10]變化的積雪密度方案，在計算雪密度時考慮了氣溫、風速、露點溫度等氣象要素的影響。研究中認為氣溫低于0℃是發生降雪的必要條件，將積雪密度分為新雪密度與舊雪經密實化過程增加的密度，其中新雪密度（ρfresh，單位：kg/m3）的計算計算公式為

式中，ρtm和ρbs分別為無風時的雪密度[6]和風速大于5 m/s 時的雪密度[38]，風速小于5 m/s 時ρbs為0。

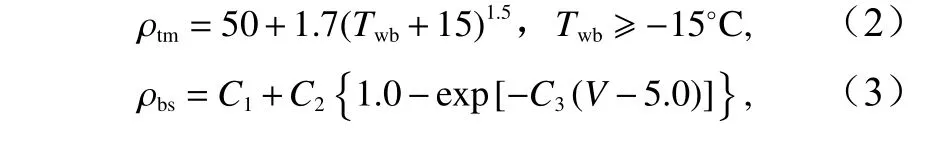
式中，Twb為濕球溫度（單位：℃）；V為風速（單位：m/s）；系數C1=25.0 kg/m3；系數C2=250.0 kg/m3；系數C3=0.2 s/m。先由式（2）、式（3）計算ρtm和ρbs，再由式（1）得到新雪密度ρfresh。

不同地理位置的雪密實化速率是不同的[39]。這里考慮了氣溫、風速兩種氣象要素對積雪密實速率ρsr（單位：kg/(m3·s)）的影響，其公式為

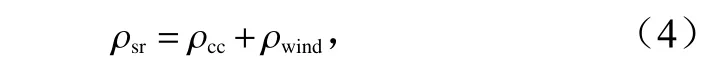
式中，ρcc和ρwind分別表示氣溫和風速引起的積雪密實速率，由式（5）、式（6）計算得出[10]：

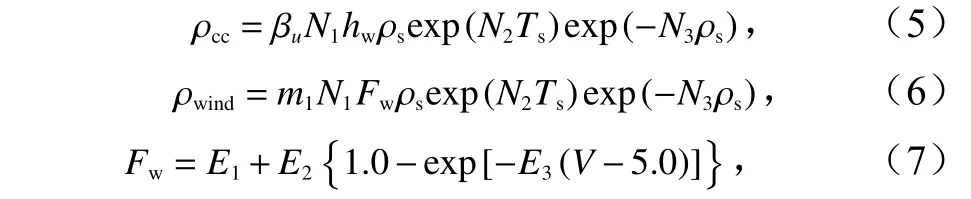
式中，βu為積雪密度速率調整因子，無量綱數，研究中設為0.1；系數N1=0.003 1 m/s；系數N2=0.081℃；系數N3=0.021 m3/kg；hw為雪轉化成水后水的深度（單位：m）；Ts為雪溫（單位：℃），采用2 m 氣溫來近似；ρs為積雪密度（單位：kg/m3）；m1是無量綱數，為0.10；Fw表示風速（單位：m/s）對積雪密度的影響程度，當風速大于5 m/s 時由式（7）計算，否則為1.0 m/s；系數E1=5.0 s/m；E2=15.0 s/m；E3=0.2 s/m[38]。積雪密實速率導致的雪密度變化還與上一時刻雪的密度、厚度有關。Snow-Model-LG 中將βu取為1，計算過程中對比分析了βu的取值從0.1～1.0 對雪厚模擬的影響，得出βu的取值對計算結果影響很小，并且取為0.1 時的結果稍好。

2.4 積雪厚度

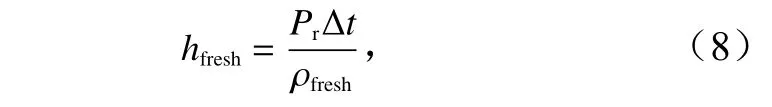
式中，hfresh為新雪厚度（單位：m）；Δt為1 d（86 400 s）；Pr為ERA5 降水數據（單位：kg/(m2·s)）。舊雪經過密實化過程后的厚度及新、舊雪疊加后的平均積雪厚度分別為

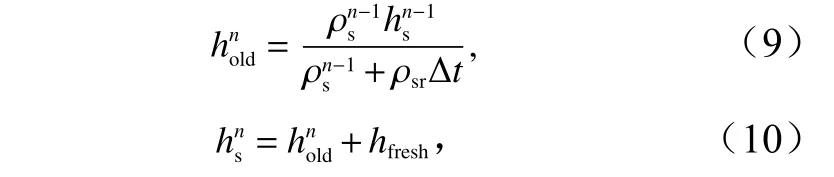
式中，上標n和n-1 分別表示第n天和第n-1 天；為第n-1 天的積雪密度（單位：kg/m3）；第n天新、舊雪疊加后的平均積雪密度等于新、舊雪的總質量除以平均積雪厚度。以上是對變化雪密度的計算，對于常數雪密度，將式（8）至式（10）中的密度變量取常數即可。

2.5 敏感性實驗方案

為了研究變化雪密度與常數雪密度對模擬PB 站積雪厚度的影響以及不同氣象要素對積雪密實化的相對重要性，這里設計了敏感性實驗A、B、C 與D。4 個實驗均采用2.4 節的方法計算積雪厚度。不同之處在于，實驗A 采用2.3 節的方法計算雪密度；而實驗B 中雪密度取常數330 kg/m3，等于海冰模式（如CICE[37]與Hamburg[40]）中采用的常數雪密度參數。實驗C 是在A 中不考慮風對密實化的影響來計算雪密度（式（6）和式（7）），實驗D 是在A 中不考慮氣溫變化對密實化的影響來計算雪密度（式（5））。

3 結果與討論

3.1 氣候模式和SnowModel-LG 的雪厚模擬現狀分析

衛星觀測數據、CESM2、NESM3 和SnowModel-LG 模擬數據的獲取時段分別是2010-2020 年的每年10 月至翌年4 月、2015 年1 月至2064 年12 月、2015年1 月至2054 年12 月和1980 年8 月至2018 年7 月，它們都存在完整降雪年數據的相同時段是2015-2018 年的每年10 月至翌年4 月。研究中對比了CESM2、NESM3 1 年（2015 年10 月至2016 年7 月）和3 年（2015年10 月至2018 年7 月）平均的數據，發現兩者在空間分布（圖2e 至圖2l 和圖3e 至圖3l）和全域平均值方面差異不大。為了讓模式有更好的時間代表性，本研究采用CryoSat-2 衛星觀測的和CESM2、NESM3、SnowModel-LG 模擬的2015 年10 月至2018 年4 月3 年平均的2 月、4 月、10 月和12 月北極圈內（66.5°N 以北）積雪厚度（圖2）討論常數雪密度和變化雪密度對模擬雪厚度結果的影響。

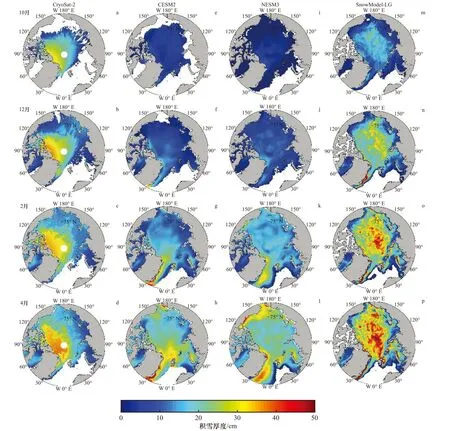
圖2 CryoSat-2 衛星觀測的（a-d）與采用不同積雪密度的模式（CESM2（e-h）、NESM3（i-l）和SnowModel-LG（m-p））模擬的北冰洋2015 年10 月至2018 年4 月的3 年平均的10 月、12 月、2 月和4 月積雪厚度Fig.2 October,December,February and April snow depth averaged between October 2015 to April 2018 observed by CryoSat-2 (a-d)and modeled by CESM2 (e-h),NESM3 (i-l) and SnowModel-LG (m-p) over the Arctic

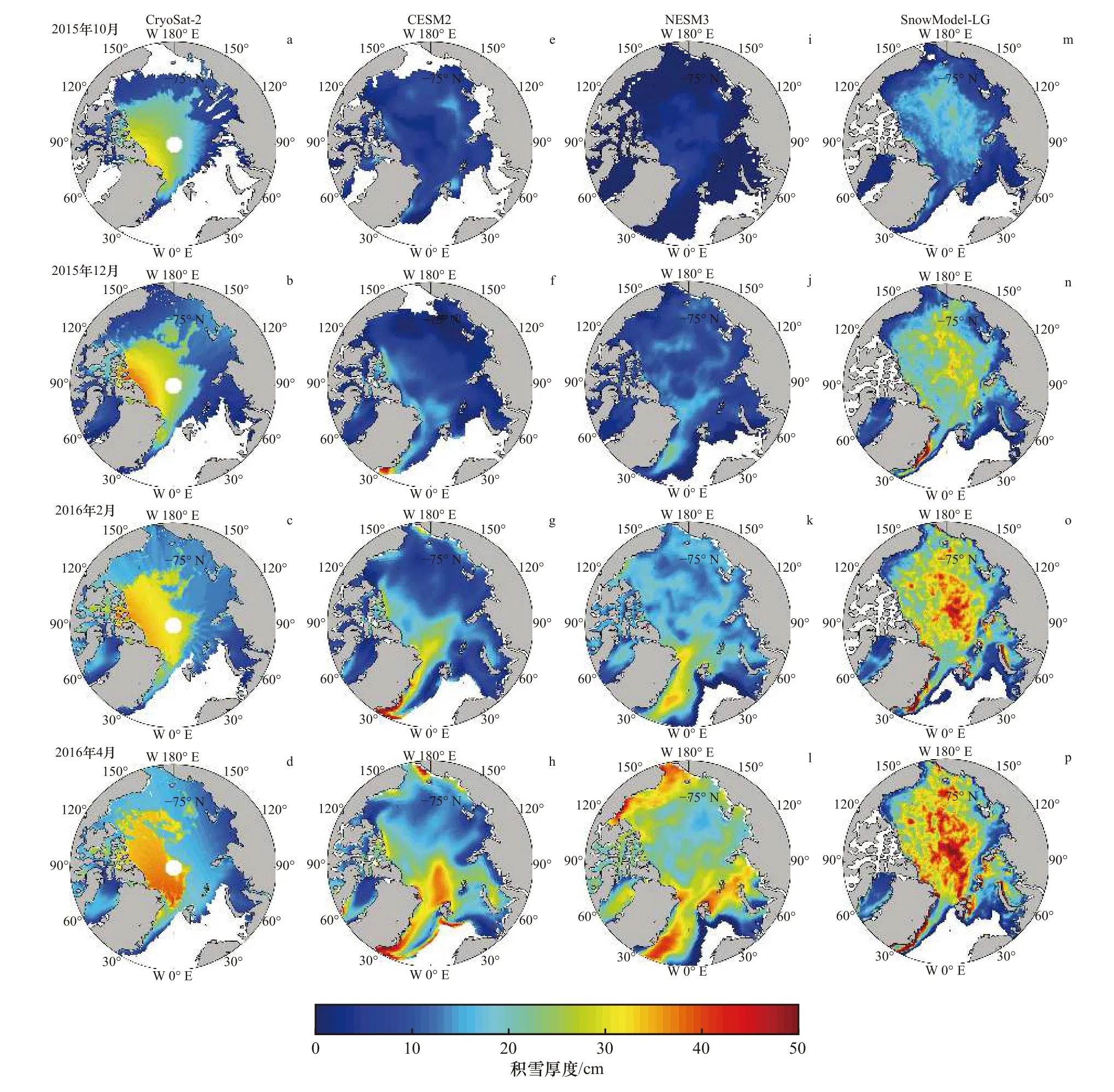
圖3 CryoSat-2 衛星觀測的（a-d）與采用不同雪密度的模式（CESM2（e-h）、NESM3（i-l）和SnowModel-LG（m-p））模擬的北冰洋2015 年10 月、12 月與2016 年2 月、4 月平均積雪厚度Fig.3 Snow depth of October,December in 2015 and Febraury,April in 2016 between observed by CryoSat-2 (a-d) and modeled by CESM2 (e-h),NESM3 (i-l) and SnowModel-LG (m-p) over the Arctic

CryoSat-2 觀測的北極圈內10 月、12 月、2 月和4 月積雪厚度基本都呈西高東低的梯度分布特征（圖2a 至圖2d），其中最大積雪厚度區域在4 月的加拿大群島北部海域（70°～90°N，30°～90°W），而拉普捷夫海（70°～80°N，105°～140°E）、東西伯利亞海（70°～80°N，140°E～180°）上積雪厚度最小。從3 個模式結果（圖2e 至圖2p）來看，10 月、12 月的積雪厚度低值區都在阿拉斯加至俄羅斯北部沿岸，但高值區不同：CESM2 和NESM3 的高值區在加拿大群島一側，與觀測值相似，但數值明顯偏小；SnowModel-LG 的高值區則僅部分分布于加拿大群島，而多數高值位于北冰洋海盆中部的廣大海區。對于2 月和4 月，3 個模式的積雪厚度高值區都與衛星觀測結果明顯不同：CESM2 和NESM3 的高值區在格陵蘭島東北側和楚科奇海；SnowModel-LG 的高值區仍在加拿大群島北側及北冰洋海盆中部的廣大海區。氣候模式CESM2 和NESM3 考慮了大氣、海洋、海冰等復雜的耦合動力過程；而SnowModel-LG是通過對遙感的逐7 d 的海冰運動和海冰密集度數據進行插值處理來實現模式的動力學過程計算，比氣候模式的動力學過程相對簡單。并且，遙感觀測數據在時間或空間上的缺測，可能會導致海冰運動結果的誤差，進而使得模擬的積雪厚度空間分布產生誤差。

CryoSat-2 觀測的北極圈內10 月、12 月、2 月和4 月的積雪厚度平均值分別為17 cm、16 cm、19 cm和20 cm；SnowModel-LG 的模擬結果分別為10 cm、17 cm、22 cm 和24 cm；CESM2 的模擬結果分別為6 cm、9 cm、15 cm 和22 cm；NESM3 的模擬結果分別為2 cm、8 cm、16 cm 和22 cm。總體上，采用常數雪密度的氣候模式模擬的積雪厚度在數值量級上比觀測結果偏小，尤其是在10 月和12 月。采用變化雪密度的Snow Model-LG 模擬的10 月、12 月積雪厚度值比CESM2 和NESM3 的大，更接近衛星觀測結果。但是這與Snow-Model-LG 在處理降水數據時將北冰洋的數據乘以了一個降水比例因子有關（對于MERRA2 和ERA5 的2009-2016 年降水場，該因子平均值分別為1.37 和1.58[10]），從而導致模擬的積雪厚度量值比氣候模式更接近觀測結果。

以上分析表明，從空間分布與平均值很難判斷出常數雪密度和變化雪密度對北冰洋積雪厚度的模擬結果產生何種影響。首先，這3 個模式的熱力學、動力學過程和降雪分布都還存在很大的不確定性誤差。CESM2 與NESM3 氣候模式考慮了較復雜的耦合動力過程，CESM2 還包括氣溶膠、海洋生物化學、大氣化學和陸地冰4 個模式分量；而SnowModel-LG 是通過對遙感數據插值處理以實現其動力學過程計算，比氣候模式的動力學過程相對簡單。其次，CryoSat-2 衛星的積雪厚度分布數據與模式的部分數據來自遙感觀測，而遙感觀測數據在時間或空間上的缺測可能會導致其出現誤差，比如CryoSat-2 觀測的積雪厚度或輸入到SnowModel-LG 中的海冰運動數據。如果海冰運動數據存在誤差，則會增加Snow-Model-LG 模擬的積雪厚度誤差。由此，本研究在保證大氣強迫場輸入、數據處理等過程相同的條件下設計了敏感性實驗，僅通過改變積雪密度方案診斷計算一維單點測站PB 站的積雪厚度，分析不同積雪密度對積雪厚度模擬的影響以及不同氣象要素對模擬積雪密度、厚度的相對重要性。

3.2 不同雪密度方案診斷計算單點積雪厚度的敏感性實驗

本文利用PB 站2018 年10 月4 日 至2019 年5 月10 日降雪累積時段的觀測資料檢驗敏感性實驗結果（圖4），研究以PB 站觀測的積雪開始連續累積（2018年10 月4 日）和完全消融（2019 年5 月25 日）的時間點為準，將降雪累積時段分為前期（10 月4 日至12 月31 日）、中期（翌年1-2 月）和后期（翌年3-5 月，積雪完全消融）3 個時期。從實測積雪厚度變化看，積雪厚度在前期主要表現為連續累積，呈波動增加的趨勢；中后期積雪厚度繼續增加，但增加幅度小于前期；后期隨著氣溫的升高，積雪厚度在5 月中旬迅速減小至完全消融。總體上，變化雪密度方案診斷計算的積雪厚度均方根誤差最小，為4.2 cm，相關系數為0.82；常數雪密度計算的積雪厚度均方根誤差次之，為4.8 cm，相關系數為0.80；僅考慮風對積雪密實化影響時得到的積雪厚度均方根誤差、相關系數接近同時考慮風、氣溫對積雪密實化影響時的結果；僅考慮氣溫對積雪密實化影響時得到的積雪厚度均方根誤差最大，為25.9 cm，相關系數為0.67（表2）。以上結果說明：變化雪密度方案有利于減小對積雪厚度模擬的誤差；其結果與觀測值的相關性更高。

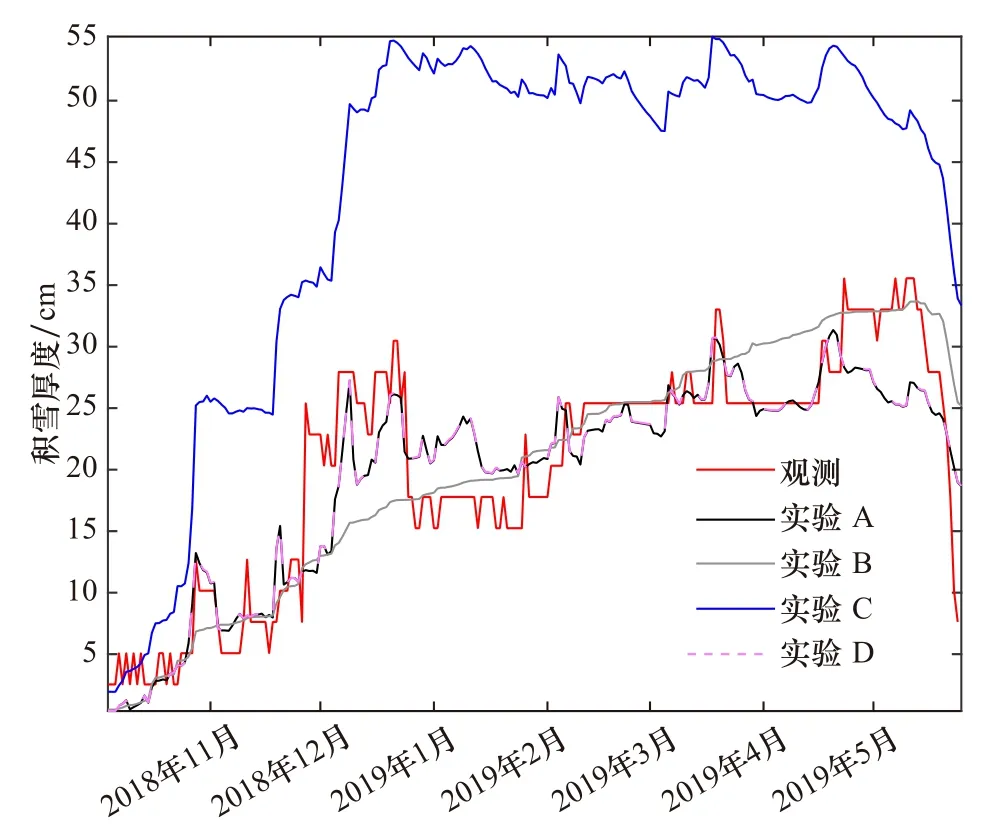
圖4 實驗A、B、C 和D 模擬的普拉德霍灣站積雪厚度和觀測值的比較Fig.4 Modeled snow depth in cases A,B,C and D at Prudhoe Bay Station,and comparison with observation

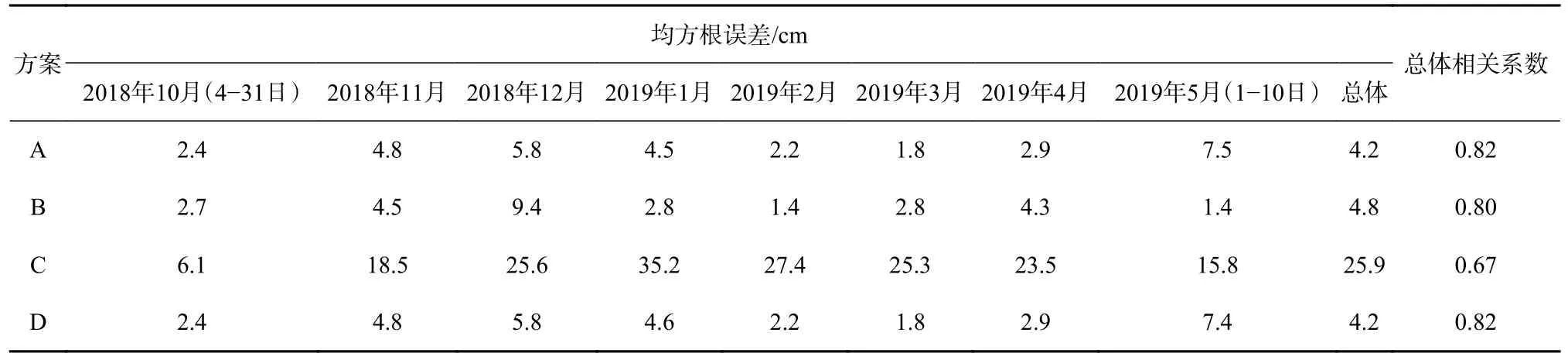
表2 實驗A、B、C 和D 模擬的普拉德霍灣站積雪厚度的均方根誤差與相關系數Table 2 Root mean square errors and correlation coefficients of snow depth in cases A,B,C and D at Prudhoe Bay Station

實驗A、B、C 和D 前期的積雪厚度均方根誤差平均值分別為4.3 cm、5.5 cm、16.7 cm 和4.3 cm，中期的分別為3.4 cm、2.1 cm、31.3 cm 和3.4 cm，后期的分別為4.1 cm、2.8 cm、21.5 cm 和4.0 cm。前期隨著積雪厚度連續增加，不斷有新雪降落累積在舊的雪層上，加上風力等作用使雪層變得更加密實，得到實驗A 的前期各月積雪厚度均方根誤差小于實驗B 和C。而實驗C 僅考慮了氣溫對積雪密實化的影響，得到的積雪厚度均方根誤差最大。中期，積雪厚度緩慢增加，注意到實驗A 的均方根誤差均值比實驗B 的大。從實驗C 可以看出，僅考慮氣溫對積雪密實化的影響時，積雪厚度均方根誤差比前期的明顯增大。到了后期，實驗B 的積雪厚度均方根誤差均值最小（2.8 cm），但實驗B 的積雪厚度變化未模擬出積雪厚度高頻變化上的特點，僅能反映積雪累積的平均過程。實驗A 的積雪厚度從5 月開始減小，比觀測和試驗B 的早，使后期積雪厚度均方根誤差比實驗B 的大1.3 cm。與實驗A、D 相比，實驗C 的均方根誤差增大了3 倍以上，表明風對積雪密實化的影響遠大于氣溫對其的影響。此外，當僅考慮氣溫對積雪密實化過程的影響時，實驗C 在觀測到積雪厚度開始累積（10 月4 日）前就有了積雪，而觀測結果表明實際從10 月4 日才出現降雪并累積。因此，模擬積雪厚度變化時考慮風對積雪密實化的影響是至關重要的。

就各月均方根誤差而言，實驗A 對于2019 年3 月的積雪厚度均方根誤差最小（1.8 cm）。因為實驗A 很好地模擬出了2019 年3 月6-9 日和17-23 日等時段的積雪厚度在幾天到十幾天時間尺度上的高頻變化，從而減小了相對誤差，并提高了與觀測值的相關性。實驗A 的5 月積雪厚度均方根誤差最大（7.5 cm）。雖然在積雪厚度量值上與觀測結果相差較大，但實驗A 模擬出了5 月中上旬積雪厚度短時間內上升、下降的高頻變化。實驗B 則不能再現雪厚在十幾天甚至幾天以內的高頻變化細節，僅反映了雪厚平均值的低頻變化。

實驗A 得出的雪密度范圍與以往研究的結果較一致（圖5）。不同學者曾對不同區域的積雪密度范圍進行了研究，如Gottlieb[6]通過擬合的經驗公式得到格陵蘭島南部的積雪覆蓋與冰川化盆地的積雪密度范圍為50～500 kg/m3，Liston 等[10]應用SnowModel-LG 模擬的冬天雪密度變化范圍為150～450 kg/m3，夏天可達到550 kg/m3，且呈現出更復雜的空間分布特征。實驗A、D 模擬的雪密度范圍為150～550 kg/m3，而實驗C 的為50～280 kg/m3（圖5），因此，變化雪密度方案計算的積雪密度范圍與以往研究的觀測或模擬結果一致，是合理的。

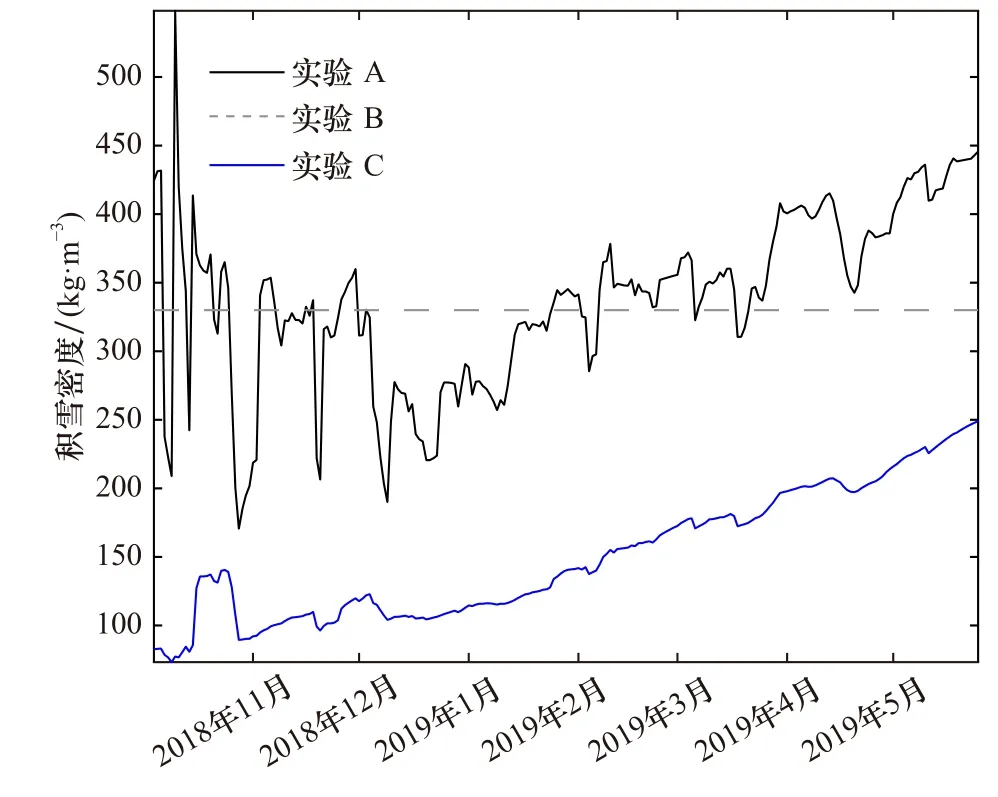
圖5 實驗A、B 和C 模擬的普拉德霍灣站2018 年11 月至2019 年5 月 積雪密度Fig.5 Modeled snow density from November 2018 to May 2019 in cases A,B,C and D at Prudhoe Bay Station

就積雪密度平均值而言，實驗A 和D 的雪密度整體平均值（330.6 kg/m3和330.0 kg/m3）接近實驗B 的常數雪密度值，而實驗C 模擬的雪密度平均值僅為其他實驗結果的一半。歷史研究結果中，Longley[41]測得北美北部群島上積雪的平均密度為332 kg/m3，Warren等[9]觀測的北極海冰上積雪平均密度為300 kg/m3，Sturm 等[42]通過SHEBA 浮標所測數據計算得出積雪密度平均值為320 kg/m3。實驗A、D 計算的2 月平均積雪密度為341.2 kg/m3，比Longley[41]測得加拿大西北地區2 月的積雪密度均值（343.3 kg/m3）小2.1 kg/m3，比Warren 等[9]測得的北極2 月積雪密度平均值（300.0 kg/m3）大41.2 kg/m3。總體上，變化雪密度方案模擬的積雪密度平均值是合理的。并且與考慮氣溫對積雪密實化的影響相比，考慮風對積雪密實化影響比考慮氣溫對其影響時得到的雪密度更接近以往研究結果。比較實驗A 模擬的2019 年2 月1 日前后的積雪密度可得，該日前的積雪密度均值為300.9 kg/m3，該日后的積雪密度均值為374.4 kg/m3，前者小于后者。上述對各敏感性實驗的模擬結果，既表明了積雪存在密實化過程，也反映了考慮這一過程對于模擬更加符合實際的積雪厚度變化的重要性。

為了進一步說明診斷計算結果的可信度，本研究比較了實驗A 和B 計算的積雪厚度與實測厚度的相對誤差（圖6）。將相對誤差進行5 點滑動平均，消除了異常值對相對誤差整體變化趨勢的影響。實驗A、B、C 和D 模擬的2018 年11 月1 日至2019 年5 月10 日積雪厚度相對誤差平均值分別為16.50%、16.02%、136.30%和16.52%。實驗C 的積雪厚度相對誤差最大，這是由于該實驗未考慮風對積雪密實化的影響。此外，實驗A 和B 在2018 年11 月至12 月初積雪密度的相對誤差變化幅度基本一致；但具體到以日為單位分析可知，實驗B 在2018 年12 月2-26 日積雪厚度相對誤差比實驗A 的平均高約16.4%；而對于2018年12 月27 日至2019 年1 月18 日的積雪厚度，實驗A 的相對誤差比實驗B 的高約19.1%。從2019 年2 月中旬至4 月下旬，實驗A 的相對誤差平均值為6.4%，實驗B 的約為9.3%。就逐月相對誤差而言，實驗A 在2019 年3 月的積雪厚度相對誤差最小（5.88%），2018 年11 月相對誤差最大（28.02%）；實驗B 在2019年5 月相對誤差最小（2.35%，5 月1-10 日），在2018 年12 月相對誤差最大（32.05%）。與常數雪密度相比，采用變化雪密度方案減小了積雪厚度最大月平均相對誤差。在模擬出積雪厚度幾天到十幾天時間尺度上的高頻變化的同時（2019 年3 月6-9 日和17-23 日等時段），實驗A 與積雪厚度高頻變化對應時段的積雪厚度相對誤差都比實驗B 的小（圖6），說明再現積雪厚度短時間內的高頻變化有助于減小模擬積雪厚度的誤差。

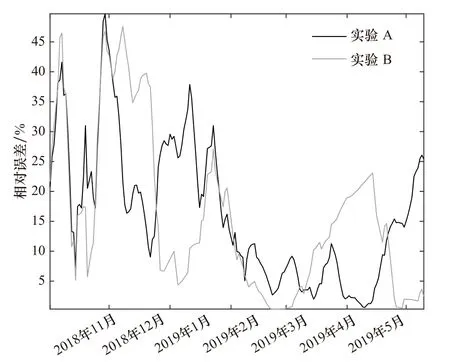
圖6 實驗A 和B 模擬的普拉德霍灣站積雪厚度的相對誤差Fig.6 Relative errors of modeled snow depth in cases A and B at Prudhoe Bay Station

4 結論

以往對積雪的研究大部分在陸地區域，積雪密度的研究經歷了從常數、經驗公式到參數化方案的過程。雪密度的影響因子及其相對重要性以及已有的一些參數化方案是否適用于氣候模式模擬極地海冰上的積雪，有待進一步探討研究。本文通過比較采用變化雪密度的SnowModel-LG 與采用常數雪密度的氣候模式CESM2 和NESM3 模擬的以及CryoSat-2 衛星觀測的2015 年10 月至2018 年7 月3 年平均的10月、12 月、2 月和4 月北冰洋積雪厚度，發現很難從不同模式的熱力學、動力學過程和模擬的降雪分布等方面得出積雪密度變化對模擬結果的影響。于是設計了4 個敏感性實驗診斷計算SNOTEL 測站PB 站的積雪厚度，并用觀測資料進行檢驗，在保證大氣數據輸入、其他處理過程相同的條件下探究采用不同積雪密度方案對于模擬積雪厚度的影響。

模擬雪密度的變化范圍與觀測結果相當，并且能夠反映出積雪厚度在幾天到十幾天時間尺度上的高頻變化。例如PB 站2018-2019 年時段的積雪厚度的高頻變化主要發生于2018 年12 月和2019 年3 月。綜合考慮氣溫與風速對積雪密實化影響得到的積雪密度變化范圍為150～550 kg/m3，其平均值（330.6 kg/m3）接近目前氣候模式采用的常數雪密度值（330 kg/m3），而僅考慮氣溫對積雪密實化的影響得到的雪密度平均值僅約為150 kg/m3。與考慮氣溫對積雪密實化的影響相比，考慮風速對積雪密實化影響下模擬的雪密度更接近觀測值。

實驗A 和實驗B 的雪厚變化差異主要表現在幾天到十幾天的尺度上，而它們在月平均的尺度上則很接近。這表明3.1 節中SnowModel-LG 與氣候模式CESM2 和NESM3 模擬雪厚的區別不是因為變化雪密度，而主要是因為大氣和海冰狀況的不同。如果3 個模式的大氣和海冰狀況一樣，則3 個模式的月平均雪厚值應該很接近。

綜合考慮氣溫與風速對積雪密實化影響的變化雪密度方案模擬的2018-2019 年降雪累積期內積雪厚度均方根誤差（4.2 cm）比采用常數雪密度方案的（4.8 cm）小。不考慮風速對積雪密實化影響時模擬的積雪厚度均方根誤差最大（25.9 cm），因此，風速對積雪密實化的影響遠大于氣溫對其的影響，在模擬積雪密度和厚度變化時必須考慮風速對積雪密實化的影響。

與常數雪密度方案相比，采用變化雪密度方案減小了模擬的積雪厚度最大月平均相對誤差。此外，采用變化雪密度方案模擬出積雪厚度在幾天到十幾天內高頻變化的同時也減小了積雪厚度出現高頻變化時段對應的相對誤差，因此，是否模擬出積雪厚度出現高頻變化時段與能否減小模擬誤差具有一定的相關性。