基于能量法及減震率的隔震簡支梁橋地震響應分析

彭剛輝 姚國文 賈宏宇 鄭史雄 李世亞

1.成都理工大學工程技術學院，四川 樂山 614000；2.重慶交通大學山區橋梁與隧道工程國家重點實驗室，重慶 400074；3.西南交通大學土木工程學院，成都 610031

橋梁安全性是需要重點考慮的問題，橋梁抗震設計需引起足夠重視［1］，減隔震設計是非常有效的一種抗震設計方法。鉛芯隔震橡膠支座具有阻尼高、耐久性好及可復位的功能［2］，廣泛應用在簡支梁橋的隔震設計中。1973年到1993年，新西蘭大部分隔震橋梁采用鉛芯隔震橡膠支座，美國已修建的隔震橋梁絕大部分也采用鉛芯隔震橡膠支座［3］。近年來，我國許多簡支梁橋采用鉛芯隔震橡膠支座進行隔震設計［4］，并對鉛芯隔震橡膠支座的隔震效果及影響因素進行了探討。石巖等［5］研究了近斷層地震動下公路橋梁鉛芯橡膠支座變形發熱及性能退化效應，討論了鉛芯溫度增量和特征強度降低率與近斷層地震動的關系。劉亨等［6］研究了鉛芯隔震橡膠支座的屈服前剛度、屈服力及剛度比對簡支梁橋隔震效應的影響。梁瑞軍等［7］通過對鉛芯隔震橡膠支座（Lead Rubber Bearing Isolation，LRB）進行參數優化，提升了LRB在隔震曲線梁橋中的隔震效果。Hassan等［8］研究地震動持續時間對基礎隔震橋梁地震反應的影響，并分析了LRB 對橋墩底部剪力、隔震耗能的影響。裴星洙等［9］基于能量原理研究了隔震結構地震響應預測法，建立了地震作用下隔震結構在最大地震響應時刻的能量平衡方程，推導出基于能量平衡的隔震結構地震響應預測公式。

地震能量可以反映地震強弱，能較為全面地體現地震頻譜特性。地震時橋梁結構處于地震能量場中，橋梁結構與地面存在能量輸入與能量耗散，輸入值與耗散值的大小直接影響橋梁結構的安全。隔震效果直接影響橋梁結構體系的耗能，采用減震率可以對隔震支座的隔震效果進行評價。眾多學者研究了鉛芯隔震橡膠支座的力學性能及減隔震措施，但從能量角度結合減震率來研究鉛芯隔震橡膠支座隔震效果的較少。本文以四川西部高烈度山區一座鉛芯橡膠隔震支座簡支梁橋為例，研究地震能量法與減震率法在隔震簡支梁橋中的應用情況及其對橋梁結構地震響應產生的影響，可為同類橋梁的減隔震設計提供參考。

1 有限元模型

1.1 橋梁模型

以一座6跨鋼筋混凝土簡支梁橋為例（圖1），主梁混凝土采用C45，橋墩混凝土采用C30；主梁采用T 梁截面，每片 T 梁質量為 76.94 t，每跨布置 10 片 T 梁，橋墩采用圓形截面。

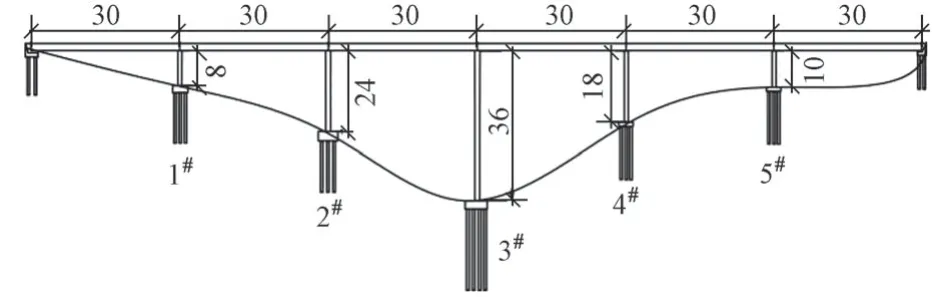
圖1 橋梁立面（單位：m）

采用有限元軟件ANSYS 建立力學數值模型，主梁、橋墩及樁基礎均采用梁單元進行模擬，樁-土作用采用土彈簧［10］，考慮梁體間的碰撞，隔震支座采用鉛芯隔震橡膠支座，全橋隔震。計算參數根據JT/T 822—2011《公路橋梁鉛芯隔震橡膠支座》取值［11］，包括鉛芯屈服力Qk、屈服前剛度K1、屈服后剛度K2、水平等效剛度Ke以及容許位移［δ］，具體參數見表1。

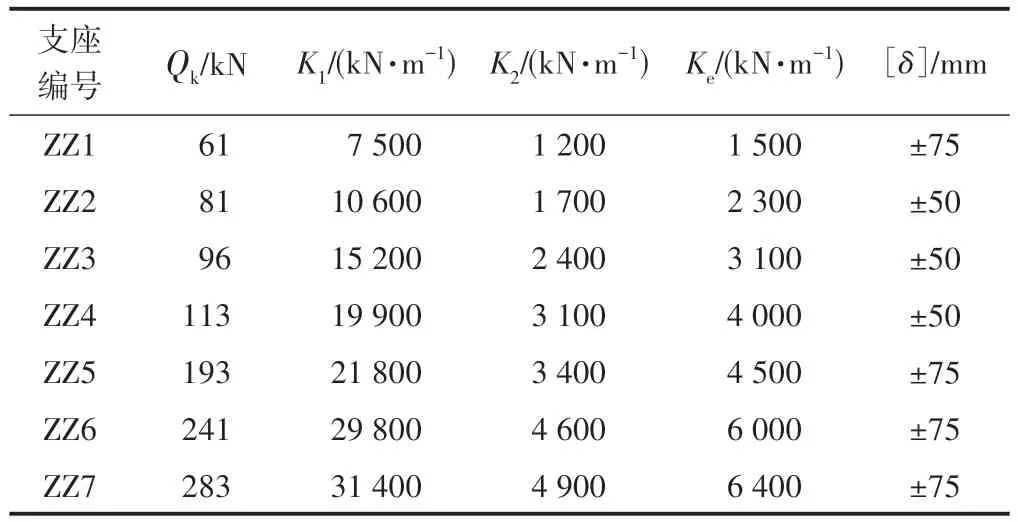
表1 鉛芯隔震橡膠支座參數

1.2 地震動輸入

地震作用下橋梁結構動力計算所用阻尼采用瑞利阻尼，利用結構前兩階周期值計算質量因子和剛度因子，采用非線性動力時程法計算橋梁結構的地震響應。根據JTG/T 2231-01—2020《公路橋梁抗震設計規范》（以下簡稱規范）可知橋梁地震反應譜曲線計算式［12］為

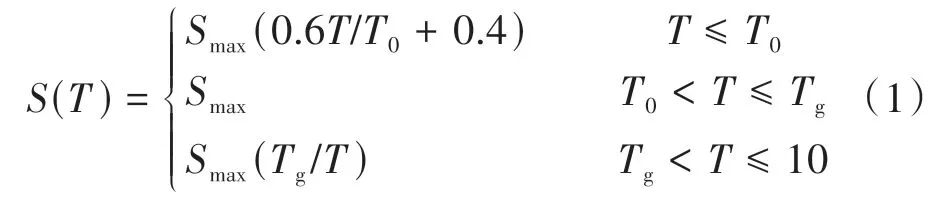
式中：Smax為設計加速度反應譜最大值；T為周期；T0為反應譜直線上升段最大周期，一般取0.1 s；Tg為特征周期。

該橋位于Ⅱ類場地，設計為第一組，烈度為8 度，由規范可得：Tg=0.35 s，峰值加速度αmax=0.3g，Smax=0.975g。將參數Tg、αmax代入程序計算生成2 條人造地震波（圖2）。

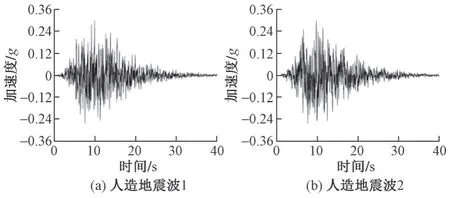
圖2 人造地震波

將參數Tg、Smax代入式（1）可得出目標反應譜曲線。根據目標反應譜，從PEER 數據庫中選取與之匹配的5條地震波對峰值加速度進行調整，見表2。

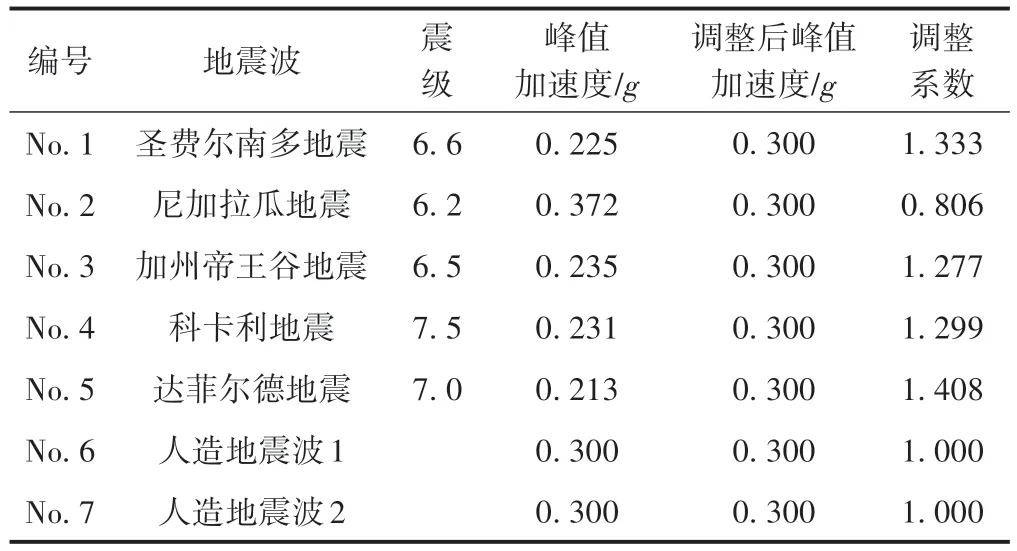
表2 地震動記錄

求出7 條地震波的加速度反應譜，并將其與目標加速度反應譜進行擬合，見圖3。可知：7 條地震波的加速度反應譜平均值與目標值較接近，擬合效果較好，可用于該橋的地震作用計算。

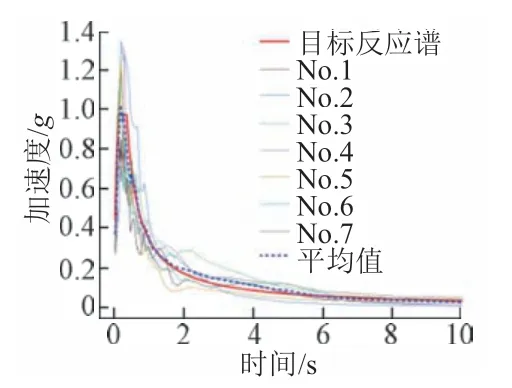
圖3 加速度反應譜曲線擬合

2 基于地震能量法的簡支梁橋隔震耗能

2.1 橋梁結構地震能量反應方程

多自由度橋梁結構體系在地震作用下相對位移的能量反應方程［13］為

超聲檢查、CT檢查及MRI檢查用于瘢痕妊娠合并子宮動靜脈瘺中檢出率無統計學意義（P＞0.05）；超聲檢查、CT檢查及MRI聯合檢測檢出率，高于單一超聲檢查、CT檢查及MRI檢查（P＜0.05），見表1。

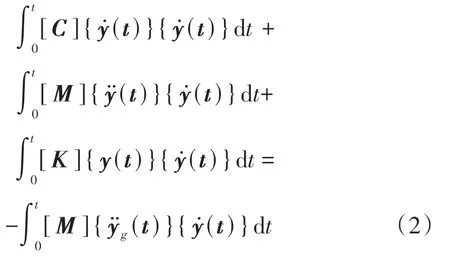
式中：［M］、［C］、［K］分別為多自由度體系的質量矩陣、阻尼矩陣和剛度矩陣為地面運動的加速度向量分別為t時刻橋梁結構體系相對于地面的位移列向量、加速度和速度。

式（2）等式左端3 項依次為結構阻尼耗能QD（t），結構體系動能QK（t），滯回耗能與彈性應變能之和QH（t）+QS（t）。式（2）等式右端項為地震總輸入能QI（t）。根據能量守恒原理，地震總輸入能與系統其他所消耗的能量之和相等，即

地震作用下，橋墩處于彈性狀態的隔震體系橋梁滯回耗能QH（t）等于隔震支座的滯回耗能，體現了隔震支座對整個結構體系滯回耗能的重要性。

2.2 隔震簡支梁橋地震能量反應分析

為了研究鉛芯隔震橡膠支座的隔震效果，對1#—5#橋墩進行同型號支座布置，共8 種工況。其中，ZZ0為普通橡膠支座（非隔震支座），為工況；ZZ1—ZZ7 支座布置對應的工況為工況2—工況8。

隔震耗能比為隔震耗能與地震總輸入能的比值，鉛芯隔震橡膠支座耗能比曲線見圖4，相同地震波不同支座時地震波采用No.3，相同支座不同地震波時支座采用ZZ3。可知：不同地震波、不同隔震支座對隔震耗能產生的影響不相同，但無法準確判斷影響程度。

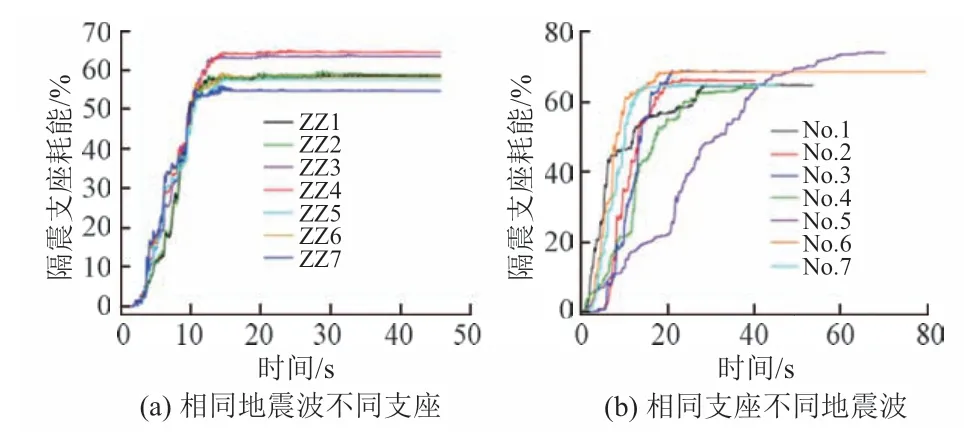
圖4 鉛芯隔震橡膠支座耗能比曲線

統計不同地震波下橋梁結構體系隔震耗能比，見表3。可知：不同工況相同地震波作用下，最大值與最小值的差值依次為13.7%、16.9%、6.2%、5.1%、11.4、4.2%、7.0%，相同工況不同地震波作用下，最大值與最小值的差值依次為8.4%、8.5%、6.8%、9.0%、15.6%、15.4%、20.2%，其差值各不相同，亦無規律可循。為了更好地表達鉛芯隔震橡膠支座對橋梁結構體系隔震耗能的影響，根據規范取7 條地震波作用的平均值作為隔震耗能評價指標。由此可知工況5的隔震耗能平均值最大，工況8的隔震耗能平均值最小，兩者相差僅8%。這說明對于鉛芯隔震橡膠支座參數（Qk、K1、K2、Ke）逐漸增大的工況，雖然隔震耗能平均值均在60%以上且不相同，但不同工況之間隔震耗能的差異性較小。

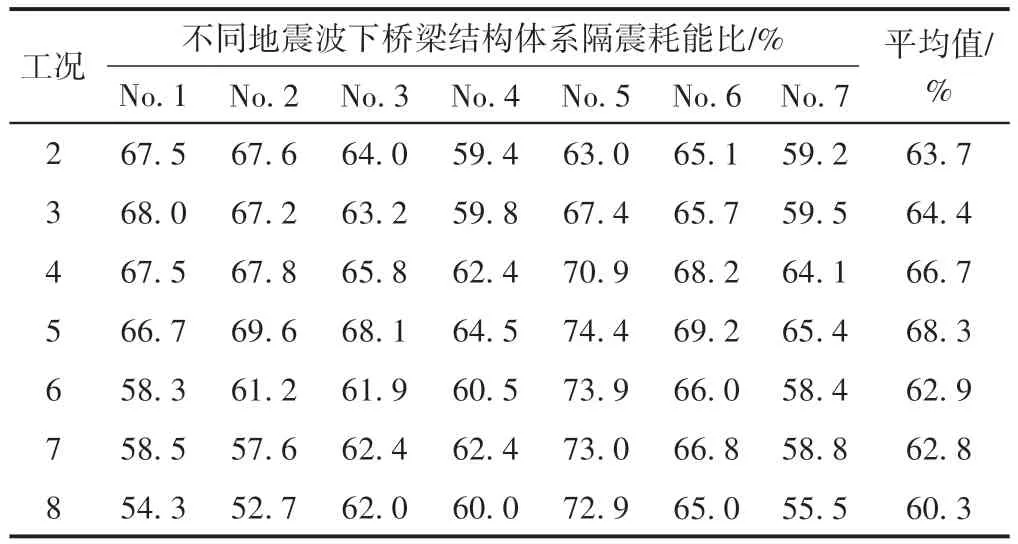
表3 橋梁結構體系隔震耗能比

相同地震波（No. 3）不同支座工況下的支座滯回曲線見圖5。可知：不同支座滯回曲線的水平位移與水平剪力各不相同。ZZ1支座鉛芯屈服力及水平剛度較小，因此水平位移較大，水平剪力較小；ZZ7 支座鉛芯屈服力及水平剛度較大，因此水平位移較小，水平剪力較大。各支座滯回曲線形狀差異較大，但滯回曲線所圍的面積相差卻較小，進一步說明各支座工況下的隔震耗能相差不大。

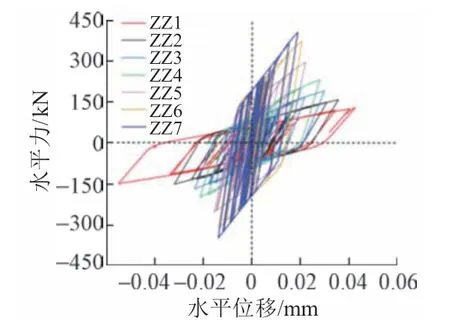
圖5 相同地震波不同支座工況下的支座滯回曲線

綜上，基于地震能量方程對隔震簡支梁橋進行隔震耗能分析，地震波及隔震支座均會對隔震耗能產生影響。由于地震波頻譜特性不同，因此在不同支座工況下采用多條地震波作用的平均值來衡量橋梁結構體系的隔震耗能。從隔震耗能平均值看，不同支座工況之間的差異較小。能量法可以分析橋梁結構體系的隔震耗能，但對橋墩的地震響應及鉛芯隔震橡膠支座的隔震效果無法作出評價。

3 基于減震率的橋墩地震響應

3.1 減震率的定義

隔震橡膠支座的減震率定義為采用隔震橡膠支座后的地震響應與采用普通支座時地震響應相比降低的百分比。計算公式為：（普通支座時橋墩地震響應-鉛芯橡膠支座時橋墩地震響應）×100%/普通支座時橋墩地震響應。

3.2 橋墩地震響應分析

因橋墩在地震作用下容易受損，嚴重的損傷會引起橋梁倒塌，故將橋墩的地震響應作為分析對象，控制參數為墩底彎矩、墩底剪力及墩頂位移。根據規范橋墩的地震響應取7條地震動計算結果的平均值。各工況下橋墩的地震響應及減震率分別見表4和表5。

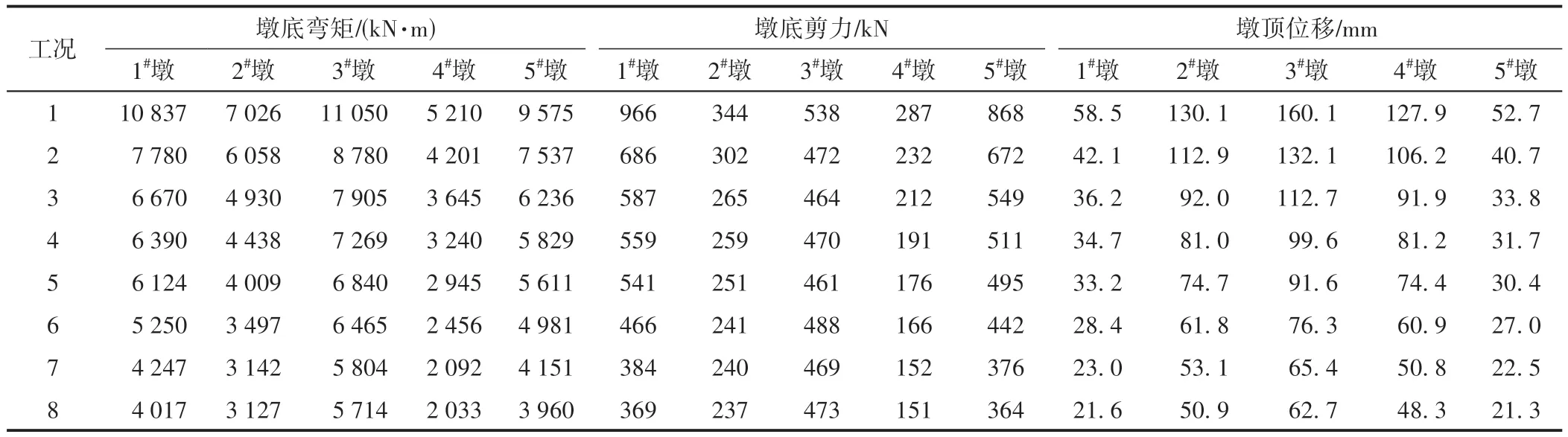
表4 各工況下橋墩地震響應

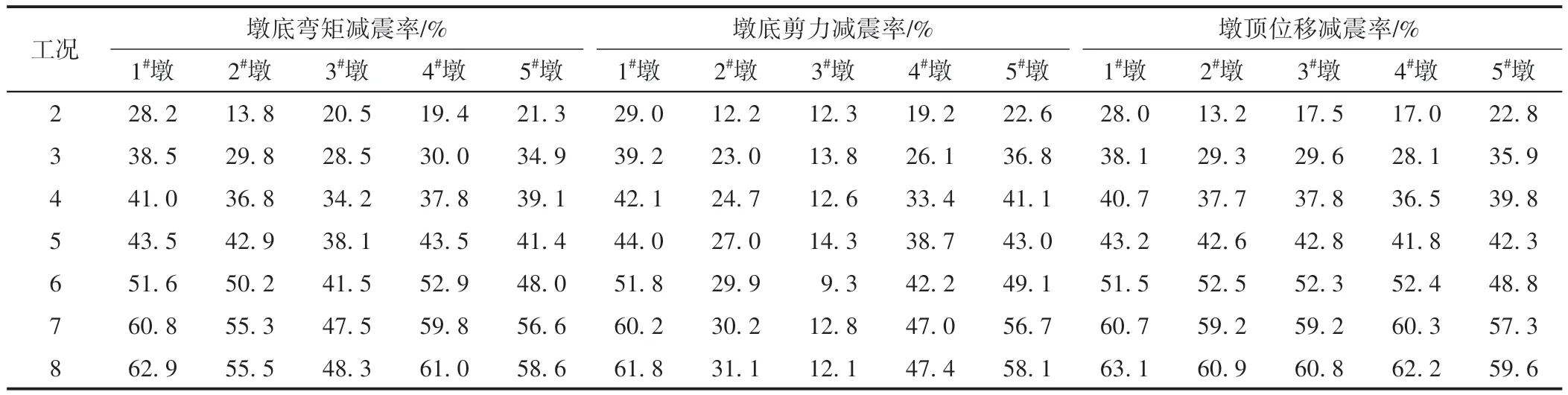
表5 各工況下橋墩減震率

由表4、表5 可知：工況2—工況8 中墩底彎矩、墩底剪力和墩頂位移總體上逐漸變小，其對應的減震率逐漸增加。地震作用下隨著鉛芯隔震橡膠支座參數的增大，橋墩地震響應減小。這是因為支座水平剛度及鉛芯屈服力變大，在一定程度上增大了由支座與橋墩組合而成的水平抗推剛度，由此減小了墩頂的位移，使得墩底的位移轉角變小，墩底的彎矩及剪力隨之變小。另外，各橋墩在不同工況下的彎矩減震率、剪力減震率及位移減震率的總和依次為1 473.7%、1 154.8%和1 525.5%，說明鉛芯隔震橡膠支座對墩頂位移及墩底彎矩的減震效果較好，對墩底剪力的減震效果稍差。

4 結論

1）利用能量法對隔震簡支梁橋進行了系統的隔震耗能評價，由于地震波頻譜特性的不同導致結構體系隔震耗能的差異性較大，因此將7 條地震波作用的平均值作為評價指標。各工況下橋梁結構體系的平均隔震耗能比較接近，即在支座滿足承載能力的前提下，當全橋采用同一型號的隔震支座時，不同隔震支座的隔震耗能相差不大。

2）利用減震率對橋墩隔震前后的地震響應進行分析，支座水平剛度及鉛芯屈服力越大，減震率越高，隔震效果就越好；鉛芯隔震橡膠支座對墩頂位移及墩底彎矩減震效果較好，對墩底剪力減震效果稍差。

3）在對簡支梁橋進行隔震設計時，地震能量法用于橋梁結構體系的隔震耗能分析，減震率用于橋墩的地震響應及鉛芯隔震橡膠支座的隔震效果分析，將兩種方法結合起來，既可對橋梁結構進行整體性的隔震耗能分析，又可對橋梁構件進行局部的隔震效果分析。