基于無應力狀態法的預應力混凝土斜拉橋主梁合龍方案

王文明 柴生波 聶寧波 魏謙 牛俊杰

1.西安科技大學建筑與土木工程學院，西安 710054；2.中鐵十五局集團第一工程有限公司，西安 710018

在斜拉橋施工過程中，主梁合龍伴隨結構由懸臂到成橋的體系轉換，是懸臂施工的重要控制內容，影響結構成橋線形及內力。合理的主梁合龍方案可以使橋梁線形平順，內力分布更優。通常情況下，主梁合龍方案是以合理成橋狀態為目標，根據施工經驗初步提出主梁合龍方案，通過倒拆法［1］和正裝迭代法［2］判斷方案是否合理。混凝土主梁施工受收縮徐變、施工荷載變化、約束條件等影響，導致結構最終成橋狀態與目標成橋狀態不閉合［3-4］。無應力狀態控制法［5-6］解決了此類問題，因此在實際施工控制中得到應用，其在預應力混凝土橋梁施工控制中的可靠性已得到驗證［7-9］。目前，關于混凝土斜拉橋主梁合龍的研究多集中在合龍施工控制方面［10-11］。從合龍段的無應力狀態出發分析混凝土斜拉橋成橋狀態線形及內力，并結合溫度影響從理論上研究合龍段對成橋線形的影響機制相對較少。

本文以一座預應力混凝土斜拉橋為研究對象，以成橋狀態為目標，通過分析三種合龍方案合龍段的無應力狀態量，對比各方案相應的成橋狀態，確定最優合龍方案，分析合龍溫度對結構成橋狀態的影響，給出合龍溫度建議。

1 無應力狀態法

1.1 斜拉索無應力狀態量

斜拉索的張拉是一個改變自身無應力長度的過程（圖1），斜拉索將由A 狀態變為B 狀態，在此期間斜拉索的無應力長度發生變化。圖中，S1、S2分別為狀態A 和狀態 B 的幾何長度；S10、S20分別為狀態 A 和狀態 B的無應力長度；T1、T2分別為狀態A和狀態B的索力。

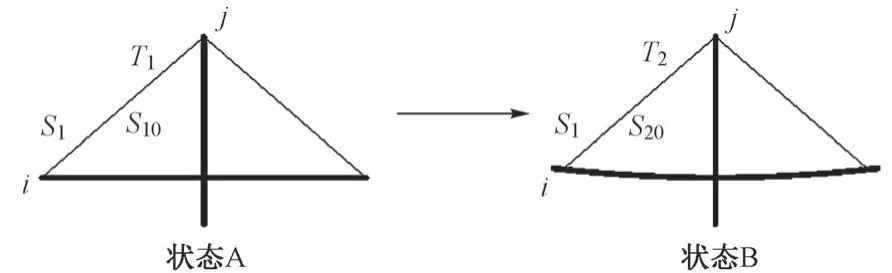
圖1 斜拉橋狀態變化

狀態A的斜拉索幾何長度為

狀態B的斜拉索幾何長度為

式(2) - 式(1)并忽略二階微量得到

式中：E為斜拉索的彈性模量；A為斜拉索截面面積。

在斜拉索i、j兩端施加單位力，假設斜拉索幾何長度變化了ε，則

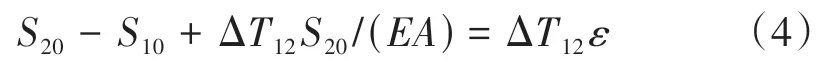
式中：ΔT12為兩狀態索力變化量。

由式（5）可知，在結構所受外荷載、支撐邊界條件不變時，斜拉索的兩種狀態下索力的變化量與無應力長度差存在一一對應的關系。

1.2 主梁無應力狀態量

主梁無應力狀態除了單元的無應力長度還包括單元的無應力曲率。平面梁單元模型（圖2）中梁單元幾何長度為l，抗彎剛度為EI。當梁單元受到外荷載作用時，梁單元發生變形，此時單元a、b兩端位移坐標分別為（ua，va，θa）、（ub，vb，θb）。

圖2 平面梁單元模型

梁單元變形后幾何長度L為

以單元未承受荷載時的曲率為初始狀態曲率，單元承受荷載產生變形后的幾何曲率可用單元變形后的位移坐標表示。梁的撓曲線微分方程為

若只考慮桿端荷載，則M(x)只能是x的一次函數，所以桿件的變形曲線一定是三次曲線。設梁單元變形后的曲線函數為

轉角θ(x)為

v(x)的一階導數為

根據梁端x= 0，x=l時的邊界條件求出c1、c2、c3、c4，將其帶入式（8）中并求二階導數可得

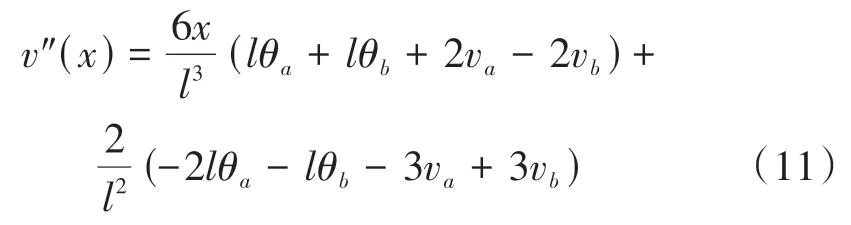
因此，梁單元a、b端曲率Ka、Kb為

由式（6）梁單元變形后幾何長度減去軸力引起的幾何變形，即可得到梁單元的無應力長度；由式（12）、式（13）除以梁端彎矩產生的幾何曲率就是梁單元的無應力曲率。對于存在合龍段分階段施工的預應力混凝土斜拉橋，為了使結構最終成橋狀態與目標成橋狀態相同，必須保證合龍段的無應力長度和無應力曲率與一次成橋結構相同。

2 工程概況

一座拱形獨塔雙索面預應力混凝土斜拉橋橋塔高130.39 m，橋塔采用C50 混凝土。主梁為（149 +133）m 非對稱橋跨布置，主梁采用C60 混凝土。其中主梁主跨（149 m 跨徑）0#—2#梁段為變高度梁段，3#—23#為標準梁段，24#梁段為合龍段，25#梁段為現澆段。主梁邊跨（133 m 跨徑）0#—2#梁段為變高度梁段，3#—16#梁段為標準梁段，17#、19#梁段為合龍段，18#、19#梁段為現澆段。斜拉索采用環氧噴涂鋼絞線成品索，其標準強度為1 860 MPa，全橋共46 對（92）根索。主梁主跨（149 m）拉索依次為1 號拉索（對應2#梁段），后續依次至22 號拉索（對應23#梁段）、23 號拉索（對應25#梁段）。對于主梁邊跨拉索，在標準段（16#梁段）之前與主跨拉索和梁段對應編號相同，在現澆段時，18#梁段對應16—19號拉索，20#梁段對應20—23號拉索。整體結構采用先塔后梁的施工順序，主梁施工采用后支點掛籃施工。結構整體布置見圖3。

圖3 結構整體布置

原主梁合龍方案為：主梁邊跨15號拉索張拉后進行邊跨17#合龍段澆筑，張拉19 號拉索后進行19#合龍段澆筑，實現邊跨合龍；在主梁主跨22 號拉索張拉后進行24#合龍段澆筑，最終實現主梁全部梁段合龍。

3 模型建立

采用有限元軟件MIDAS/Civil建立全橋模型，橋塔與主梁均采用梁單元模擬，斜拉索采用索單元模擬。斜拉索與橋塔、主梁之間均采用剛性連接，橋塔與主梁采用剛性連接模擬塔梁固結，橋塔底部固結，梁端支座彈性連接。全橋設計基準溫度為15 ℃，模擬主梁合龍溫度時通過單元溫度荷載進行施加，在合龍前激活溫度荷載，合龍后去掉溫度荷載。全橋模型及主梁標準梁端見圖4。

圖4 全橋模型及主梁標準梁端

4 合龍方案分析

4.1 合龍方案優化

根據目標成橋索力計算斜拉橋目標成橋狀態的無應力索長，在控制施工過程中保持無應力索長不變，根據原主梁合龍方案進行施工模擬。根據有限元計算結果可知，邊跨和主跨同時張拉18 號拉索時，主梁邊跨18#現澆段端部被拉起。因此，為了盡量保證梁段在自然狀態下合龍，控制合龍段兩端無應力曲率相同，可在張拉17 號拉索后進行邊跨19#合龍段澆筑。為保證邊跨19#合龍段兩端無應力曲率為0，合龍段的無應力長度為初始設計長度2 m，可在17#合龍段澆筑時進行19#合龍段澆筑。因此，提出兩種新的合龍方案，主梁主跨合龍順序不變，主梁邊跨有所改變。方案1：15 號拉索張拉后進行邊跨17#合龍段澆筑，17 號拉索張拉后進行邊跨19#合龍段澆筑。方案2：15 號拉索張拉后，同時進行邊跨17#、19#合龍段澆筑。

4.2 不同合龍方案無應力狀態分析

為保證合龍時主梁線形連續，合龍前合龍段預留的長度就是合龍段澆筑長度，即無應力長度。合龍段兩端對應的曲率即為合龍段的無應力曲率。

提取三種合龍方案下合龍前合龍段兩端節點位移坐標（計入配重影響）。由于合龍段在澆筑前未受到軸力和彎矩作用，因此將合龍前合龍口兩端變形帶入式（6）、式（12）、式（13），計算合龍段的無應力長度和兩端對應的無應力曲率，見表1。

表1 各合龍方案對應合龍段的無應力狀態量

由表1 可知：不同合龍方案下無應力長度不是設計值2 m，兩端無應力曲率不為0；主梁按照合龍方案2進行施工時，17#、19#、24#三個合龍段的無應力長度及曲率均小于其他兩種方案對應的參數值。因此，為了盡量保證合龍段澆筑時無應力狀態與初始設計值接近，選擇方案2。

4.3 不同合龍方案成橋狀態對比

為驗證方案2 是否為最優合龍方案，對比三種方案的成橋狀態。不同合龍方案主梁線形對比見圖5。

圖5 不同合龍方案主梁線形對比

由圖5 可知，由于主梁施工過程中受混凝土收縮徐變的影響，三種合龍方案主梁施工完成后成橋線形與合理成橋狀態有所差異。原方案、方案1 和方案2中主梁主跨最大變形分別為65.45、63.31、61.92 mm，主梁邊跨最大變形分別為47.08、46.22、49.31 mm；有限元模型中合理成橋狀態的主梁主跨和邊跨最大變形分別為57.63、52.31 mm。因此，按照方案2 進行主梁施工時，主梁線形更接近合理成橋線形。

三種主梁合龍方案下，塔頂位移有所不同，原方案、方案1、方案2 的塔頂位移分別為21.76、19.50、16.00 mm。說明基于無應力狀態量優化后的合龍方案，塔頂位移有所減小，且方案2的塔頂位移最小。

不同合龍方案主梁應力見圖6。可知，三種合龍方案下，主梁上下緣應力均為壓應力，由于存在橫隔板，主梁縱向應力分布呈現鋸齒形狀。主梁上下緣最大應力均為方案2 對應的主梁應力，其值分別為-9.50、-9.60 MPa。對于主梁上緣應力，不同合龍方案主要影響主梁邊跨的兩個合龍段及其兩個邊跨現澆段的主梁上緣應力，對其他位置的應力影響較小。原方案的主梁上緣壓應力最小，方案2 的主梁上緣壓應力最大。對于主梁下緣應力，三種合龍方案的應力相差較小。

圖6 不同合龍方案主梁應力

綜上，不同合龍段無應力狀態影響成橋階段主梁線形及內力，應選擇合龍段無應力狀態量接近初始設計值時的方案2進行主梁合龍施工。不同合龍方案主要影響主梁及橋塔線形，對于主梁上下緣應力影響較小。按照方案2 進行主梁合龍時，主梁線形最接近目標成橋線形，且塔頂位移最小。

5 合龍溫度影響分析

主梁合龍受施工環境因素的影響，不能完全保證合龍時溫度與設計基準溫度相同。因此分析主梁合龍溫度對主梁成橋線形及內力影響尤為重要。基于方案2進行合龍溫度的影響分析。

5.1 系統溫度取值

工程所處地址為四川省廣元市，根據氣溫數據調查及實測結果顯示，2021年四川省廣元市月平均最低氣溫在1月份，為1 ℃；月平均最高氣溫在7月份，為33 ℃。1月最高氣溫為14 ℃，最低氣溫為-3 ℃；7月份最高氣溫為36 ℃，最低氣溫為18 ℃。

根據當地氣溫數據及GB 50666—2011《混凝土結構工程施工規范》［12］規定，混凝土拌和物入模溫度不應低于5 ℃，且不高于35 ℃。因此，選取合龍溫度為5、10、15、20、25 ℃進行主梁合龍溫度影響分析。

5.2 主梁懸臂端合龍配重

主梁合龍時，在斜拉索作用下主梁懸臂段與現澆段存在高差，通常采用調整索力或在主梁懸臂端施加配重來調節合龍口兩端高差，使合龍口兩端高程盡量保持一致，保證主梁線形平順。本文采用施加配重的方式進行高差控制。在不同合龍溫度下，主梁懸臂端所需配重會隨之改變，以合龍口兩端高程為控制目標，不同合龍溫度對應的主梁懸臂端配重見圖7。可知，隨著合龍溫度的增加，主梁懸臂端配重逐漸減小。因此，施工過程中需根據合龍溫度調整配重。

圖7 不同合龍溫度下主梁懸臂端配重

5.3 不同合龍溫度成橋狀態

在合龍前設置合龍溫度，合龍后恢復至設計基準值溫度15 ℃。不同合龍溫度下主梁和橋塔位移見圖8。

圖8 不同合龍溫度下主梁和橋塔位移

由圖8 可知：①合龍溫度對主梁線形影響較大。隨著合龍溫度的升高，主跨主梁豎向位移不斷減小。合龍段之前，邊跨主梁豎向位移隨合龍溫度的升高不斷增大，合龍段之后的主梁豎向位移，隨著合龍溫度的升高而不斷減小。合龍溫度為5 ℃時，主梁主跨最大豎向位移為66.08 mm，邊跨最大豎向位移為48.59 mm。合龍溫度為25 ℃時，主梁主跨最大豎向位移為58.58 mm，主梁邊跨最大豎向位移為49.76 mm。②合龍溫度對橋塔線形的影響較大。隨著合龍溫度的升高，橋塔頂部位移不斷減小。合龍溫度為5 ℃時，橋塔頂部最大位移為21.14 mm，合龍溫度為25 ℃時，橋塔頂部最大位移為11.57 mm，塔頂位移減小了45.3%。在橋塔與主梁固結位置（即塔高35.39 m處），橋塔位移受主梁縱向位移的影響，橋塔位移不斷減小。當合龍溫度為25 ℃時橋塔位移為0.04 mm，相比合龍溫度為5 ℃時位移減小了98%。若合龍溫度繼續升高，將導致橋塔此位置出現反彎點，下塔柱出現負彎矩。因此，為了使橋塔頂部產生較小位移，且橋塔與主梁固結位置不出現反彎點，主梁合龍溫度需控制在25 ℃以內。

不同合龍溫度主梁應力見圖9。可知，主梁全截面均處于受壓狀態，合龍溫度主要影響主梁邊跨現澆段及其合龍段的應力，且隨主梁合龍溫度的升高，主梁邊跨現澆段及合龍段上緣應力在逐漸增大，對于主梁其他位置的上緣應力影響較小。對于主梁各位置的下緣應力，合龍溫度的影響也較小。

圖9 不同合龍溫度主梁應力

為分析合龍溫度對主梁三個合龍段的影響程度，對比不同合龍溫度下，17#、19#、24#三個合龍段的上下緣應力，見表2。

由表2 可知，成橋階段三個合龍段的上下緣應力均為壓應力，且下緣壓應力大于上緣壓應力，上下緣應力與合龍溫度之間呈線性變化。隨著合龍溫度的升高，三個合龍段的上緣壓應力逐漸增大，下緣壓應力逐漸減小，上下緣應力差也在不斷減小。主梁合龍溫度為5 ℃和25 ℃時，17#、19#、24#三個合龍段的上緣應力分別增大了3.94%、9.68%、2.88%，下緣應力分別減小了2.05%、1.31%、1.43%，上下緣應力差分別減小了7.67%、21.48%、6.91%。說明主梁合龍溫度對邊跨19#合龍段的影響最大。

在邊跨19#合龍段澆筑后，當結構溫度恢復到設計基準溫度時，19#合龍段下緣出現少許拉應力，應力隨合龍溫度的升高而逐漸增大。合龍溫度為20 ℃時，下緣應力為壓應力，其值為2.67 kPa；合龍溫度為25 ℃時，下緣應力為拉應力，其值為1.70 kPa。因此，為避免主梁合龍時邊跨19#合龍段出現拉應力，合龍溫度應控制在25 ℃以內。

綜上，主梁按照合龍方案2進行施工時，需控制合龍溫度在25 ℃以內。

通過式（6）、式（12）、式（13）計算合龍溫度25 ℃時主梁合龍段的無應力狀態量，對比設計基準溫度與25 ℃時的無應力長度及無應力曲率，見表3。

由表3 可知，主梁合龍溫度為25 ℃時，合龍段無應力長度及無應力曲率均小于合龍溫度為15 ℃時對應的無應力狀態量，且更加接近初始設計時合龍段的無應力狀態量。從理論上進一步說明了合龍溫度在25 ℃以內時，合龍溫度越高對結構變形與受力越有利，施工完成后的成橋狀態更接近目標成橋狀態。

6 結論

1）合龍段的無應力狀態不同，主要影響主梁及橋塔線形，對主梁上下緣應力影響較小，可選擇在合龍段的無應力狀態量接近初始設計值時的合龍方案進行主梁合龍施工。

2）預應力混凝土斜拉橋主梁邊跨合龍時，為控制主梁合龍段無應力狀態可在懸臂端施加配重，控制合龍段的無應力狀態。隨著合龍溫度的升高，主梁懸臂端配重逐漸減小。

3）隨著合龍溫度的升高，主梁和橋塔的最大變形均有所減小。合龍溫度在25 ℃以內時，受合龍溫度影響最大的合龍段在施工及成橋階段均不會出現拉應力。隨著合龍溫度的升高，合龍段的無應力狀態更接近初始設計的無應力狀態，接近25 ℃時主梁合龍最優。