基于并行融合機制的改進遺傳算法求解HFSP調度問題

張 源 陶翼飛 王加冕

(昆明理工大學機電工程學院 云南 昆明 650500)

0 引 言

混合流水車間調度問題[1](HFSP)是流水車間[2]調度問題的推廣，其特征是在某些工序中存在并行機器，其目的是指在一定時間內對加工工件的排序和加工設備的分配進行優化使某些性能指標達到最優。考慮切換時間的HFSP是指在混合流水車間調度問題的基礎上引入了機器依次加工不同工件時的切換準備時間[3]，由于加入了工件之間切換時間的因素[4]，使研究的問題與實際更為接近，成為現階段混合流水車間調度領域研究的新方向。

引入并行進化機制的遺傳算法[5]是對傳統遺傳算法[6]的優化，可以提高算法的尋優質量。目前引入并行進化機制的遺傳算法主要運用于路徑規劃[7]問題的優化，也有學者將其用于求解車間調度問題。Belkadi等[8]對混合流水車間調度問題，以最大完工時間為目標，采用并行遺傳算法進行求解并與標準遺傳算法的結果進行比較，證明了該算法可以提高求解質量。Rubiyah等[9]提出了一種求解作業車間調度問題的混合并行遺傳算法(PGA)，該算法基于異步群體和自主遷移進行迭代更新，通過對不同規模問題進行仿真實驗，證明了該算法能夠在一定程度上求解出更優的完工時間。在近幾年中的研究中，Luo等[10]針對動態混合流水車間問題，提出一種基于優先級的并行混合遺傳算法進行求解，通過仿真實驗證明了該算法的優越性。Zhu等[11]針對多目標混合流水車間問題，提出了基于灰熵分析的并行遺傳算法進行仿真實驗，結果表明該算法能有效解決多目標車間調度優化問題。Fu等[12]提出了一種基于特殊交叉變異策略的多種群并行遺傳算法對作業車間調度問題進行求解，實驗結果表明該算法能求解出更優的解。

文獻研究表明，并行遺傳算法在求解HFSP時，能夠改善求解質量，但由于缺乏關于遺傳算法的改進研究，使得引入并行機制后的算法仍存在收斂速度慢、易陷入局部極值的缺點，且多數文獻以完工時間[13](makespan)為目標進行優化，忽略了對加工不同工件時機器切換時間的研究。因此，針對上述問題，本文以考慮工件切換時間的混合流水車間調度問題為研究對象建立仿真模型，優化目標為總工位切換時間(Total Station Switching Time，TSST)，并提出一種基于種群并行融合機制的改進遺傳算法(PIGA)進行求解，最終將總工位切換時間(TSST)作為各算法的性能指標進行對比，驗證了本文算法的有效性。

1 問題描述

在考慮切換時間的HFSP中，假設共有J個工序組成，其中至少有一個工序存在一臺以上的不相關并行機設備，并且相鄰工序間存在暫存緩沖區。每個工件需要依次經過J個工序進行加工，工件在每道工序中只能選擇該工序中的一臺機器進行加工，工件在不同機器上加工時間不同，加工不同工件時機器的切換時間不同，加工相同工件時機器不需要切換時間。已知工件在所有設備上的加工時間和各工件之間的切換時間。為方便描述問題，定義參數如表1所示。

表1 數學模型定義參數

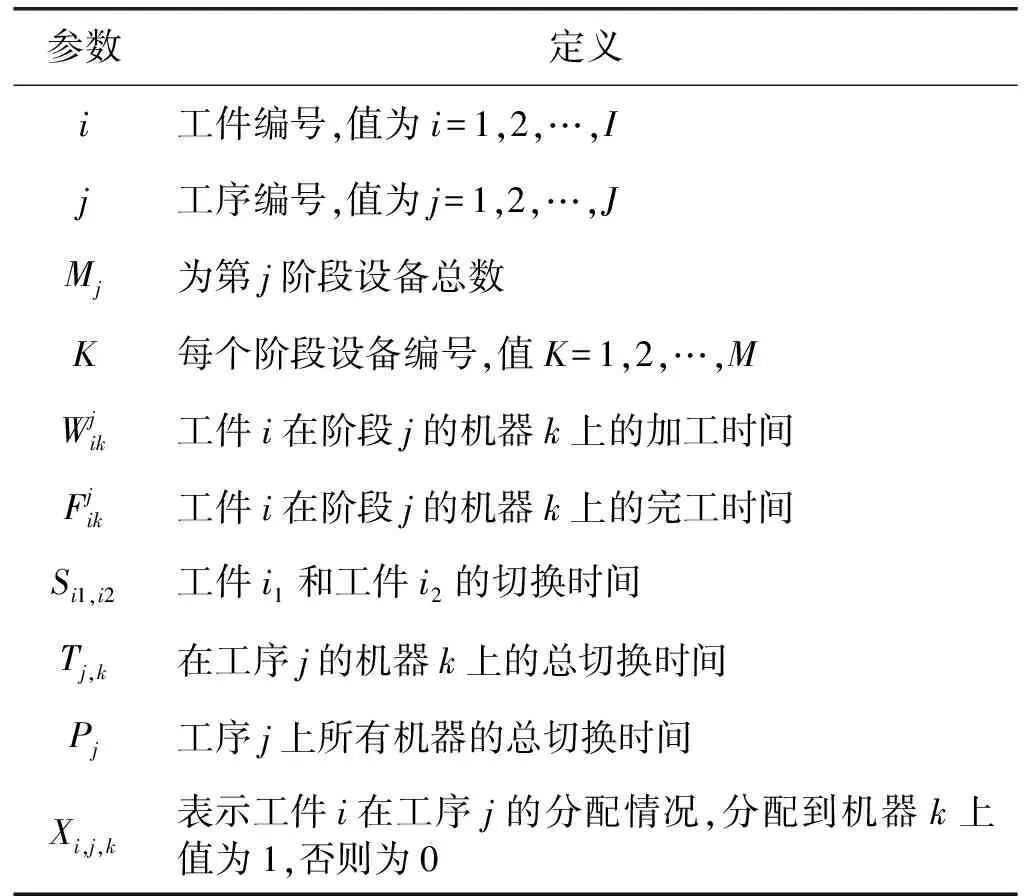
續表1

假設所有設備的切換時間只與加工工件順序相關；所有設備加工第一個工件時不需要切換準備時間；同一時間每臺設備只能加工一個工件；不同工序間有無限暫存區；問題優化目標是求解最小化總工位切換時間，即：

minCmax

(1)

考慮切換時間的混合流水車間調度問題的數學模型存在的約束條件及計算公式如下：

(2)

(3)

Si1,i2>0i1≠i2

(4)

(5)

(6)

式(2)為總工序切換時間計算公式及目標函數；式(3)為各個工序中所有機器的總切換時間；式(4)說明，任意兩個不同工件之間的切換時間必須大于0；式(5)說明同一時間，每臺機器只能加工一個工件；式(6)表示如果在工序j的機器k上依次加工工件i1和工件i2，那么工件i2在工序j機器k上的完工時間應大于等于工件i1在工序j的機器k上的完工時間、工件i1和工件i2的切換時間、工件i2在工序j的機器k上的加工時間三者之和。

2 并行融合機制的改進遺傳算法求解

遺傳算法(Genetic algorithm，GA)在HFSP中應用較為廣泛，但是標準遺傳算法由于在個體選擇和交叉變異概率方面的局限性，使算法全局搜索能力降低且出現早熟現象。因此本文結合并行融合拆分機制、精英保留策略[14]和自適應遺傳因子[15]對遺傳算法進行改進，建立了基于并行融合機制的改進遺傳算法，該算法有效克服了傳統遺傳算法易陷入局部極值的缺點。

2.1 編碼和解碼

編碼采用基于工件編號的實數編碼，即染色體中的各元素值代表對應的工件編號。解碼的目的是確定工件的加工順序和各工序設備的分配情況，其中染色體中的元素值序列代表工件進入混合流水車間的初始加工順序，后續階段加工工件的排序按前階段工件完工時間的先后順序進行加工。工件在各工序并行設備的分配根據先到先服務法則[16](First In First Seved，FIFS)進行安排，即優先安排最早進入暫存區隊列等候的工件進行加工。

2.2 種群初始化及適應度函數

初始種群產生的方法為：在均勻分布(Uniform Distribution)中隨機產生I個不重復的數字來建立初始種群，種群中的每個染色體由一個一維矩陣組成，染色體長度表示加工工件的個數。

本文優化的目標是最小化總工序的切換時間，但在遺傳算法迭代過程中保留的是適應度值最大的個體，應取目標函數的倒數作為適應度函數，由于切換時間以秒為單位計算，目標函數計算結果較大，所以為方便觀察比較，在目標函數倒數的基礎上再放大100倍，即第g代的第n條染色體的適應度函數為：

fg,n=100/Cg,n

(7)

式中：n∈{1,2,…,N}，N為每代的染色體數目；Cg,n為第g代的第n條染色體的總切換時間。

2.3 并行融合拆分機制

由于隨機生成的初始種群增加了算法尋優過程中的不確定因素，使得算法的最優解質量和收斂速度等方面的結果并不理想。因此本文在遺傳算法的迭代進化中引入一種基于多種群的并行融合拆分機制，該機制是指對遺傳算法進行并行設計，同時在并行計算中加入了種群個體間的融合拆分策略，通過對多個種群的分布式并行處理，不僅提高了算法的求解速度和運行效率，而且由于增加了種群規模和個體間的融合拆分，使得種群個體的多樣性得以維持和豐富，增加了算法的求解空間，降低了陷入局部極值的可能性，提高了求解質量。

如圖1所示，并行融合拆分機制是指將m個種群個體進行融合，融合后按某種規律重新差分為m個種群的過程。其中：bmn為種群m的第n個染色體；am×n為種群融合后的第m×n個染色體，且fa1≥fa2≥…≥fam×n；Bm為融合拆分后的第m個種群。并行融合拆分機制的具體操作為：

(1) 若滿足合并條件，將m個種群的個體進行融合，融合后通過仿真輸出所有個體的適應度值并保留最優個體。

(2) 將融合后的種群個體按適應度值大小進行降序排列，并根據排列順序重新編號，其中a1、am×n分別為融合種群的最優和最差個體。

(3) 將融合種群個體的序號按公差為m的等差數列重新拆分為m個種群，并用最優個體替換各種群中的最差個體，如拆分后種群B1的最差個體為a1+m(n+1)，則將融合種群的最優個體a1與該個體進行替換，其余種群同理進行保優操作。

(4) 保留拆分后的各種群，進行遺傳操作。

圖1 并行融合拆分機制示意圖

2.4 基于精英保留策略的個體選擇機制

在傳統的遺傳算法中，選擇操作采用輪盤賭[17]的方式，用適應度值對每代染色體進行評價，適應度值大的染色體被選中的概率也高，但該方法并不代表適應度值低的染色體不會被選中，若適應度值低的染色體被選中進入子代,則會對最終尋優結果的質量產生影響。因此本文采用精英保留策略的方法進行個體選擇,該策略是指在種群進化過程中選擇適應度值較高的個體進行復制，替換較差個體進行后續遺傳操作，并且將適應度最好的精英個體直接保留到下一代的過程。通過對優良個體進行保留復制,增強其繁衍能力，保證種群精英個體的基因序列不被破壞，提高算法的收斂速度和尋優解質量。具體操作為：

(1) 將種群中的染色體按適應度值大小降序排列。

(2) 排列后將前50%的染色體進行復制并替換后50%的染色體組成待配種群，并將最優個體保留到子代中。

(3) 保留選擇后的待配種群，進行后續的交叉變異操作。

2.5 改進自適應遺傳因子設計

在遺傳算法求解不同規模的調度問題時，很難確定最佳的交叉變異概率值，使算法過早收斂無法求解出全局最優解。而自適應交叉變異因子可以根據某些條件自行調整交叉變異概率，以達到或接近其最佳值,從而能較好地改善尋優解質量。因此本文采用基于進化代數和適應度值變化的自適應遺傳因子替換固定的交叉變異概率。

當染色體適應度值趨于早熟或多數個體集中于局部最優時，為跳出局部極值并延續優良個體的基因結構,應適當降低交叉概率增加變異概率，以達到快速尋找最優解的目的；當染色體適應度差距較大或種群個體在解空間中分散分布時，為利于優良個體的生存并保持染色體之間的差異性，應適當增加交叉概率減小變異概率[18]，以幫助種群在尋找完最優解后快速收斂。綜上所述,本文改進自適應交叉變異概率計算公式如下：

(8)

(9)

式中：Pc為交叉概率；Pcmax、Pcmin分別表示交叉概率的最大值和最小值；Pm為變異概率；Pmmax、Pmmin分別表示變異概率的最大值和最小值；favg為當前種群個體平均適應度值；fg,n為第g代第n個個體的適應度值；fmax為當前種群中最大的適應度值；fmin為當前種群中最小的適應度值；g為當前迭代次數；G為總的迭代次數。

在改進自適應遺傳因子中，交叉算子為相鄰個體間的PMX交叉，即隨機選擇兩個交叉點，交換染色體之間的片段，交換后的染色體采用部分映射進行修復。變異算子為兩點變異法，即在染色體中隨機選擇兩個位置的基因進行互換。

2.6 并行融合機制改進遺傳算法步驟及流程

本文在上述改進自適應遺傳算法的基礎上引入并行融合拆分機制構建最終的改進遺傳算法。算法總流程如圖2所示，具體步驟如下：

Step1隨機生成m個指定規模數量的種群作為改進遺傳算法的初始子種群。

Step2分別通過計算機仿真輸出m個種群中對應個體的適應度值。

Step3基于精英保留策略對各種群中的優良個體進行選擇操作。

Step4基于改進自適應遺傳算法進行種群個體的交叉變異操作。

Step5是否滿足終止條件，若滿足輸出優化結果；若不滿足轉Step 6。

Step6是否滿足合并條件，若滿足轉Step 7；若不滿足轉Step 2。

Step7將m個種群的個體進行融合，并按適應度值降序排列。排列后序號按公差為m的等差數列重新拆分為m個種群，并轉Step 2。

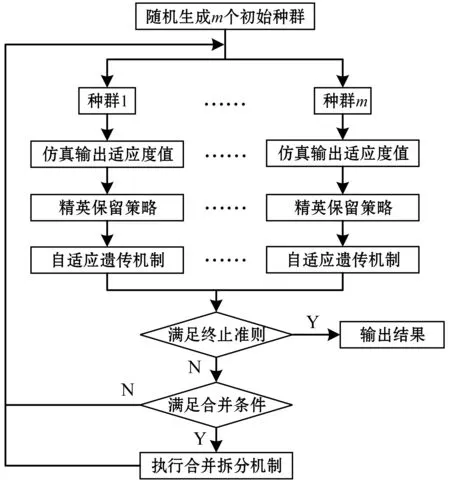
圖2 引入并行融合機制的改進遺傳算法流程

3 仿真實驗

本文進行的仿真實驗的混合流水車間實例[19]為某鋼鐵廠生產企業加工12個工件，加工過程由煉鋼、精煉、連鋼、軋制四道工序組成，四道工序的并行機數量分別為3、3、2、2。仿真模型在Plant Simulation軟件中建立，如圖3所示。

圖3 混合流水車間仿真優化模型

混合流水車間仿真模型由控制參數、程序仿真和數據統計三個模塊組成，其中程序仿真模塊中用Simtalk語言編寫算法和模型調度程序。數據統計模塊將工件之間的切換時間、工件在各機器上的加工時間、算法求解結果等數據進行記錄。控制參數模塊為仿真運行過程中需要調用的參數，并顯示當前種群的實時數據。各工件之間的切換時間服從X(min)～U[1,10]均勻分布如表2所示。

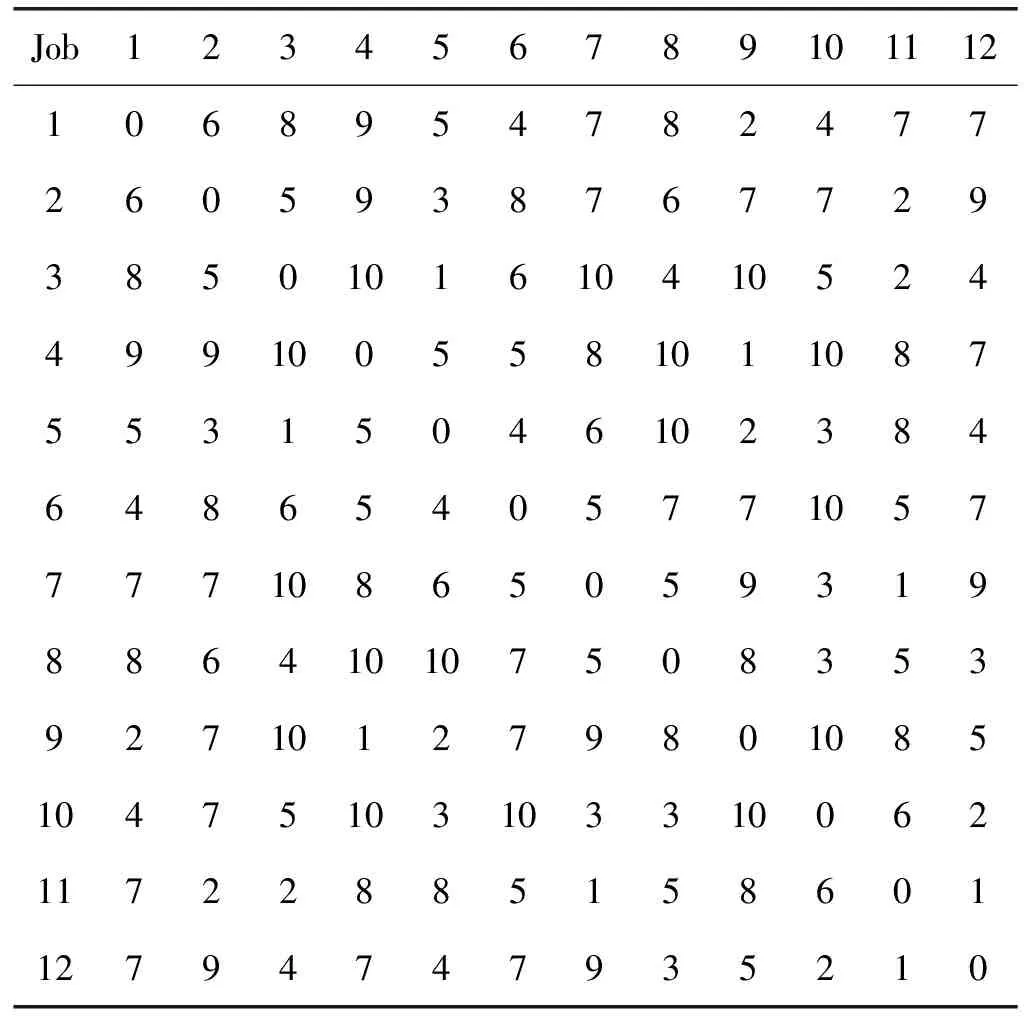
表2 工件切換時間

仿真模型在Plant Simulation軟件中運行，PIGA將各初始子種群分配到對應的處理器并行運算，每個處理器完成獨立的串行遺傳算法。設置并行融合機制的種群數m為2，滿足合并條件的迭代次數為100，交叉概率的極值為[0.6,0.9]，變異概率的極值為[0.05,0.15]。各算法的最大迭代次數Gmax為300，每代種群個體數量N為50。

4 結果分析

分別將標準遺傳算法(GA)、自適應遺傳算法(Adaptive Genetic Algorithm，AGA)和基于種群并行融合機制的改進遺傳算法(PIGA)在仿真模型中各運行10次進行比較。表3為對比結果，表中給出了各算法求解的最小值(Min)、平均值(Avg)、最大值(Max)、平均耗時(CPU)和平均收斂代數(Avg-FI)。

表3 各算法性能指標對比結果

如表3所示，由尋優解質量可得，PIGA求解的最小值、平均值和最大值均優于其他兩種算法，且最優解的極差僅為2，具有較好的穩定性和尋優能力。由運行時間可得，由于PIGA中引入了并行融合拆分機制，增加了種群數量，使該算法的實現過程更復雜，但PIGA中各子種群是在多個處理器中分布式運行，因此雖然算法的復雜性得到了提升，但運行時間與自適應遺傳算法基本一致，且求解質量也得到了改善，表明了該算法在復雜程度更高的情況下，能用相同的時間求解出更優的解，具有較好的運算效率。由收斂代數可得，PIGA的平均收斂代數明顯小于其他兩種算法，表明該算法在迭代搜索中能快速收斂到最優解，具有較好的收斂性。綜上所述，在迭代次數相同的情況下，PIGA具有更優的全局搜索能力、運行效率和收斂速度，從而驗證了該算法的有效性和優越性。

圖4和圖5為各算法的迭代曲線和最優解甘特圖。在迭代曲線中,GA和AGA分別在175和165代發生尋優停滯現象，陷入局部極小值。而PIGA在113代就收斂到最優解116，有效避免算法趨于早熟。在甘特圖中工件加工時間的條形圖下方顯示了該工件的切換準備時間，由于各設備加工首個工件時不需要切換準備時間,因此在甘特圖中各工位第一個加工時間的條形圖下方沒有顯示切換準備時間。從圖5中可得工件的完工時間為343 min，雖然加工時間較長，但優化目標是總工位切換時間，所以該結果反映的是工位切換準備時間最少的情況，即各設備加工時間下方的切換時間條形圖最短。

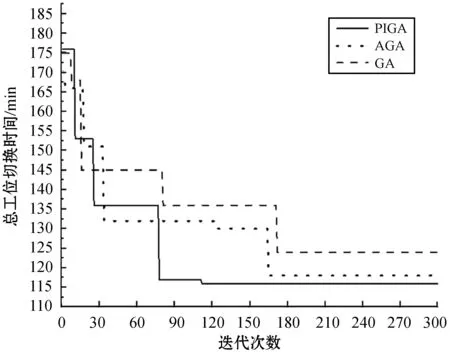
圖4 改進前后GA迭代曲線

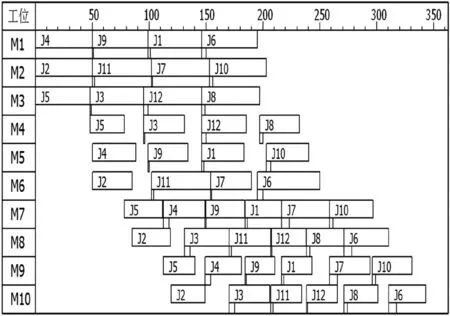
圖5 最優解甘特圖

5 結 語

本文在傳統遺傳算法的基礎上引入并行融合拆分機制、精英保留策略和自適應遺傳因子，提出一種基于種群并行融合機制的改進遺傳算法，并以總工位切換時間為目標對混合流水車間調度問題進行求解。通過仿真結果的對比分析，驗證了本文算法的有效性，為并行遺傳算法的改進研究和應用提供了一定的參考價值。