潤滑作用下平面正弦鋼球傳動機構法向接觸剛度研究
李美求,陶文杰,鄭瑞波,寧林飛,華劍
1.長江大學機械結構強度與振動研究所,湖北 荊州 434023 2.中國石化江漢油田分公司江漢采油廠,湖北 潛江 433123
平面正弦鋼球傳動機構是一種輕量化的活齒結構,不僅豐富了傳動機構的種類多樣性,而且還符合油氣裝備智能化工業領域的發展需求,尤其是在油氣開采井下作業過程中,由于井眼空間限制,小型輕量化的活齒傳動結構具有良好的應用前景。因此,關于平面正弦鋼球傳動機構的機械性能需要提出更高的設計標準,以提高材料機械性能的穩定性[1,2]。其中,活齒與其他機構元件之間的接觸特性是評價機構承載能力和使用壽命的重要標準。如果鋼球-軌道接觸面的接觸剛度過小,那么機構承受載荷的傳動元件將產生不可逆轉的塑性變形和接觸疲勞損傷。并且,通常情況下鋼球-軌道接觸面都處于潤滑狀態。因此對接觸面在潤滑條件下的接觸剛度進行研究,歸納總結出接觸面微觀形貌和材料性能參數對接觸面接觸剛度的影響規律具有重要的理論和實際應用意義。
長期以來,國內外許多研究學者對粗糙接觸面的接觸特性都進行了大量研究[3,4],其中以Majumdar和Bhushan提出的M-B分形理論最具有代表性,但是M-B分形理論忽略了彈塑性臨界變形狀態[5]。隨后,溫椒花等[6]、王南山等[7]研究人員又建立了一個包含彈性、彈塑性變形、塑性變形3種變形狀態的分形力學模型;孫見君等[8]建立了接觸面之間與測量尺寸無關的力學分形模型;CHEN等[9]進行了考慮摩擦應力因素的球面結合面法向接觸剛度分形模型基礎研究。
以上接觸模型并沒有考慮潤滑作用,實際上,大部分傳動機構元件之間的接觸面靠潤滑介質來降低磨損[10]。因此很多學者開始研究在潤滑作用下的接觸剛度,肖會芳等[11]提出了混合潤滑狀態下粗糙接觸面的法向剛度模型;GASNI等[12]以超聲波的方式測量球體與圓盤之間的接觸剛度;李玲等[13]等把潤滑液剛度與固體表面接觸剛度相結合得到新的法向接觸剛度模型。
筆者基于分形理論,建立了平面正弦鋼球傳動機構中主動圓盤-鋼球接觸面的法向接觸剛度模型。然后由固體接觸面的接觸剛度模型推導出潤滑介質的接觸剛度模型,由此實現粗糙接觸面的固體接觸剛度與潤滑液的接觸剛度相結合,得到平面正弦鋼球傳動機構在潤滑作用下接觸面法向接觸剛度的計算模型,利用數值計算的方法歸納分析了相關參數對法向接觸剛度的影響規律。
1 平面正弦鋼球傳動機構接觸模型的建立
1.1 潤滑作用下的接觸狀態
平面正弦鋼球傳動機構的傳動元件主要包括:主、從動圓盤、保持架和鋼球等[14],活齒鋼球在正弦曲線形狀的半圓軌道上轉動,如圖1所示。
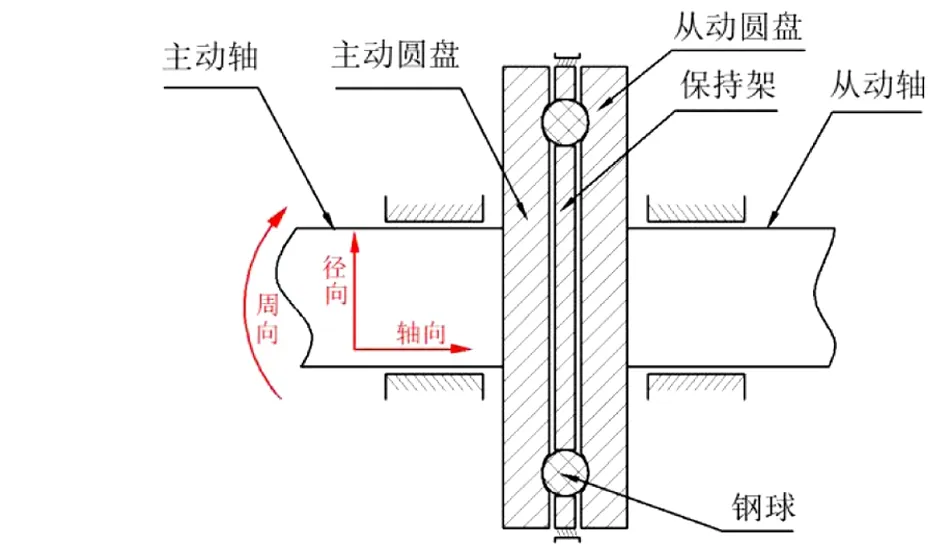
圖1 平面正弦傳動機構示意圖
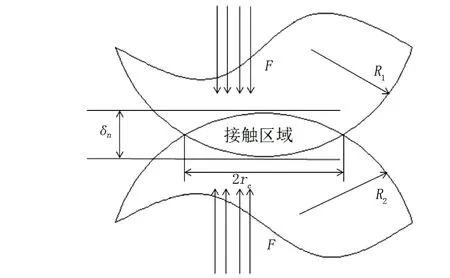
主、從動圓盤與活齒鋼球之間均為球體與半圓軌道的接觸形式,保持架與活齒鋼球之間為球體與平面的接觸形式,其中保持架可視為曲率半徑趨近于無限大的圓形軌道。因此,主、從動圓盤-鋼球及保持架-鋼球的接觸方式可以轉化為鋼球-半圓軌道接觸形式的問題來分析,潤滑作用下,他們之間的間隙由潤滑液填充,如圖2所示。
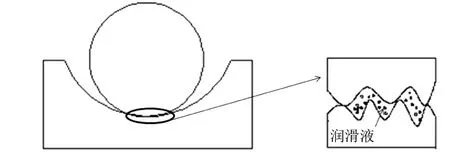
圖2 潤滑作用下鋼球-半圓軌道接觸示意圖
將活齒鋼球與其他傳動原件的接觸問題轉化為粗糙球體與粗糙圓柱內切的模型,此時的接觸區域已經由光滑的曲面接觸轉化為粗糙的曲面問題。該模型更加細化考慮了加工的真實面貌,更有利于接觸特性的研究。
1.2 粗糙接觸面分形接觸表征
2個粗糙曲面接觸可以等效為單粗糙面模型探究,如圖3所示。粗糙面輪廓上的曲線可以由W-M函數表示[15]:
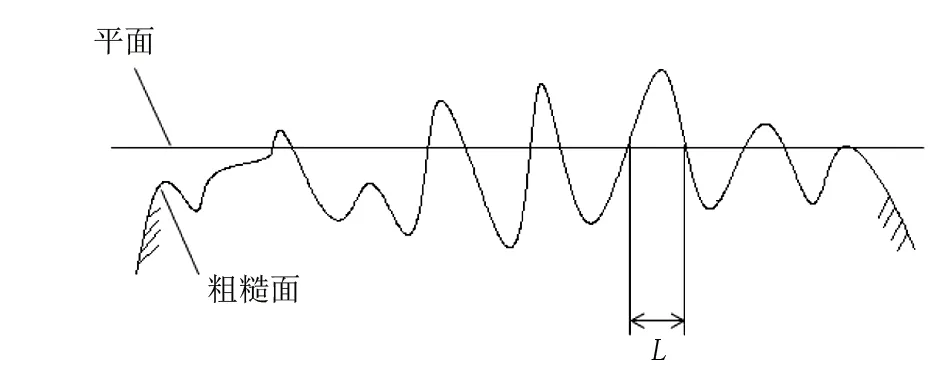
注:L為微凸體隨機表面的采樣長度。
(1)
式中:z(x)表示微凸體高度;x為輪廓位移坐標;D為接觸面的分形維數;G為粗糙度幅值;γ為服從正態分布的隨機接觸表面,通常γ=1.5,nl為最低截止頻率對應的序數。
可以看出z(x)由D、G、nl決定,D和G可以由W-M函數的功率譜獲得。
1.3 粗糙接觸面微凸體分布函數修正
M-B分形接觸中微凸體的面積分布函數[15]:
(2)
式中:a為接觸面微凸體面積;al為最大的接觸面微凸體面積。
真實接觸面積Ar為:
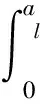
(3)
由臨界接觸點面積ac計算彈性接觸面積Are和塑性接觸面積Arp:
1)當al>ac時
彈性接觸面積為:
(4)
塑性接觸面積為:
(5)
總的接觸面積為:
Ar=Are+Arp
(6)
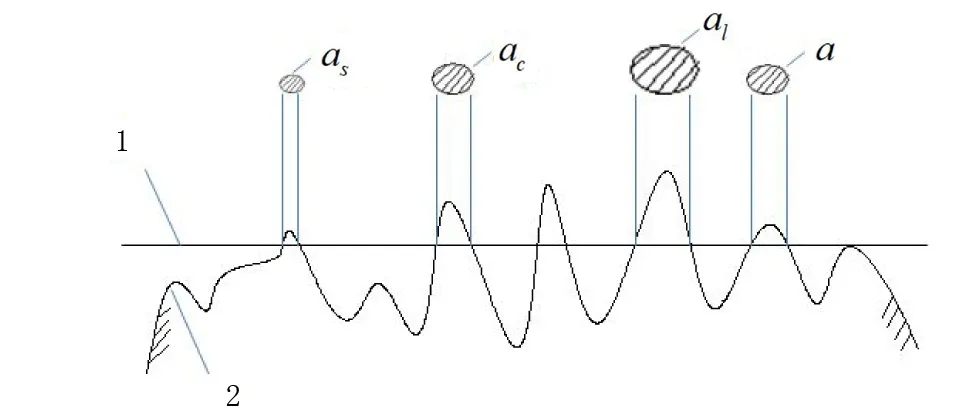
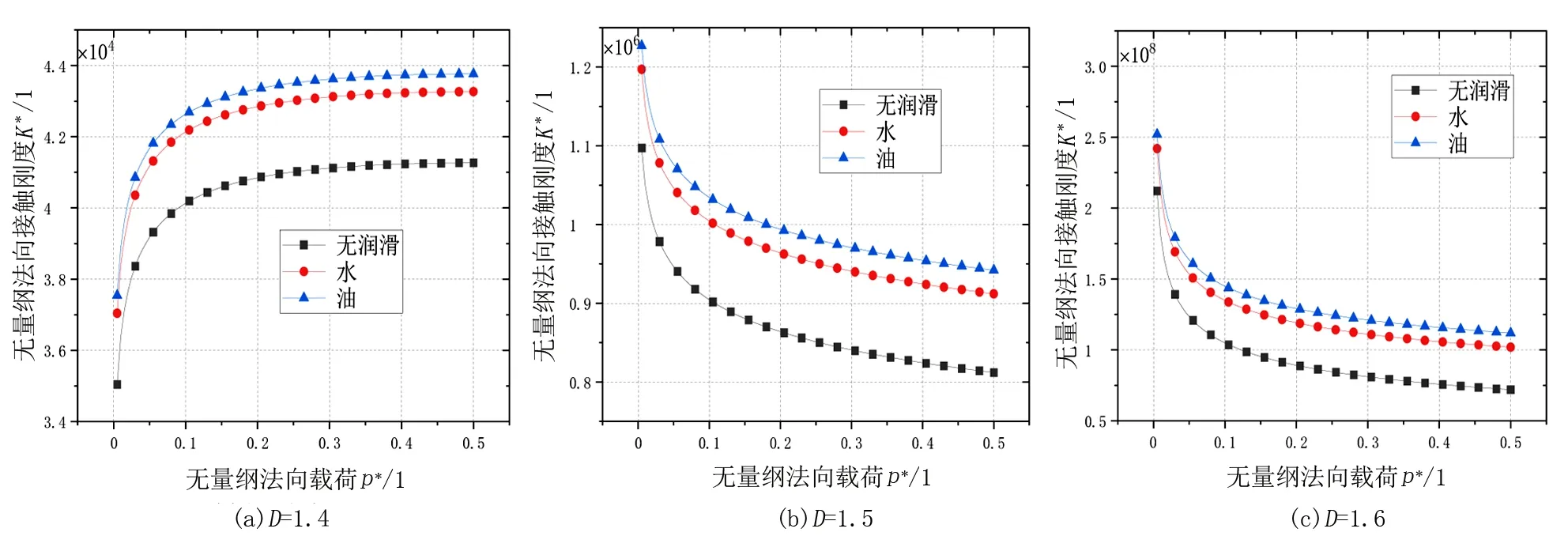
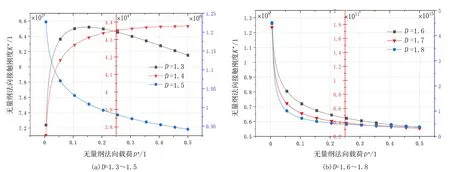
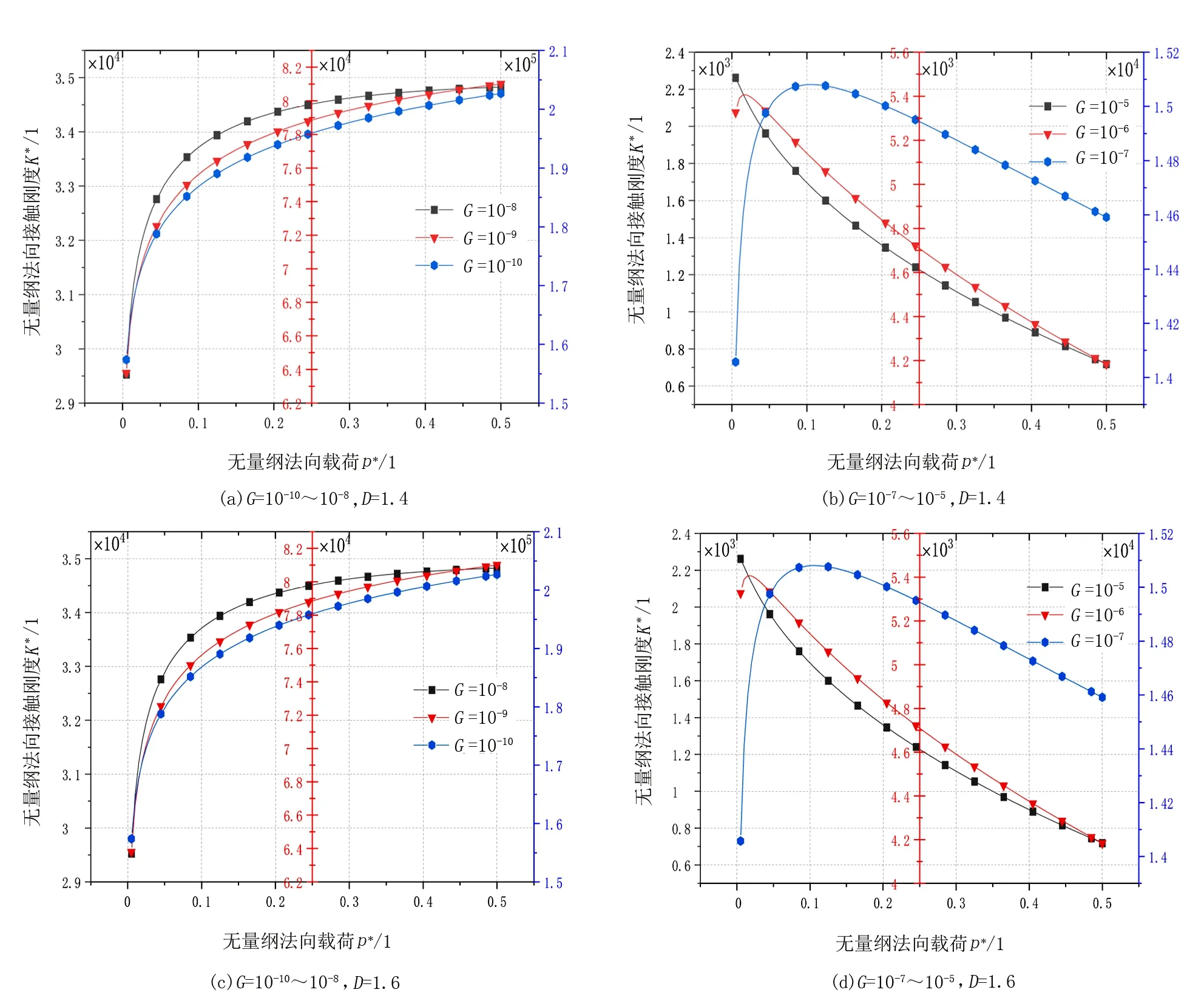
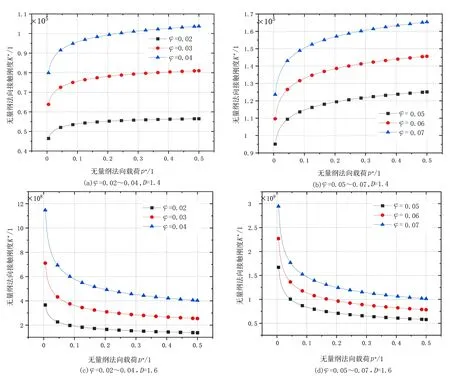
2)當al (7) 平面正弦鋼球機構中的接觸形式為曲面接觸,若將分形模型合理地運用到傳動機構的接觸特性中去,需構造一個如圖2所示接觸形式的微凸體面積分布函數n(a)修正系數λ,修正后微凸體接觸面積分布函數n′(a)為: n′(a)=λn(a) (8) 式中:λ為接觸面修正系數。 根據微凸體面積分布函數n(a)可以構造出鋼球-半圓軌道接觸面微凸體面積分布函數的修正系數λ的函數表達式為: (9) 式中:R1為軌道半徑;R2為鋼球半徑(假設R1>R2);Ee為綜合彈性模量。 由圖4可以看出,接觸面修正系數λ隨著鋼球半徑的增大呈現先增大而后趨于平緩的趨勢,且λ不超過1。其原因在于隨著鋼球半徑的增大,鋼球與半圓軌道的曲率半徑逐漸趨近于相等,此時鋼球與半圓軌道的外輪廓互相包覆,兩個表面接觸面積增大。 圖4 鋼球半徑與接觸面修正系數λ關系 以單微凸體受力變形模型為研究切入點,基于分形接觸理論推導出主動圓盤-鋼球接觸面微凸體彈塑性變形的臨界面積計算公式,從而建立出主動圓盤-鋼球固體接觸面的法向接觸剛度分形模型,然后利用固體表面的接觸剛度模型建立潤滑液的接觸剛度模型。 2個半徑為R1和R2的微凸體接觸剛度模型,如圖5所示。當法向載荷F作用到2個接觸的微凸體上表面時,就會產生一個半徑為rc法向位移量為σn的接觸變形區域。 圖5 單微凸體法向接觸剛度模型 接觸載荷與接觸變形之間的關系表示為: (10) (11) (12) 式中:Re為主動圓盤-鋼球的曲率系數;Ee為主動圓盤-鋼球的綜合彈性模量;a0為接觸變形區域面積。 其中,Re和Ee的表達式分別為: (13) (14) 式中:E1和E2分別為主動圓盤和鋼球材料的彈性模量;v1和v2分別為主動圓盤和鋼球材料的泊松比。 根據式(10)、(11)和(12),單微凸體的法向接觸剛度kn可以表示為: (15) 平面正弦鋼球傳動機構中主動圓盤-鋼球接觸面由無數個微凸體構成,在實際研究中,兩粗糙接觸面之間的研究問題簡化為單粗糙面接觸剛度模型,如圖6所示。 注:a為微凸體的接觸面積;as為微凸體最小接觸面積;al為微凸體最大接觸面積;ac為主動圓盤-鋼球接觸接觸面微凸體發生彈塑性臨界變形的面積;1為剛性平面;2為粗糙接觸面。 平面正弦鋼球傳動機構中主動圓盤-鋼球接觸面為曲面,需引入前面所建立的修正系數λ,得到鋼球-圓盤接觸面載荷與真實接觸面積之間的函數關系式[16]。 (16) (17) (18) (19) 2)當al≤ac時,微凸體發生塑性變形,接觸面總載荷為: (20) 將單微凸體的法向接觸剛度kn向多微凸體法向接觸剛度進行推廣,結合接觸面微凸體分布函數n(a)對式(15)兩邊進行積分,可以得到: (21) 在式(21)中,最小微凸體接觸面積 可以無限趨近于0。因此,式(21)可以改寫為: (22) 假設主動圓盤-鋼球接觸面微凸體發生彈塑性臨界變形的面積為ac,那么: 當al>ac時,主動圓盤-鋼球接觸面發生彈塑性變形; 當al≤ac時,主動圓盤-鋼球接觸面發生塑性變形,接觸面剛度kn為0。 式(22)的積分將由0增大到ac,此時接觸面微凸體法向接觸剛度的計算式為: (23) 主動圓盤-鋼球接觸面微凸體臨界接觸面積ac與最大微凸體接觸面積al的計算式為: (24) (25) 式中:kμ為摩擦力的修正因子;μ為摩擦系數。 將接觸面微凸體分布函數n(a)以及接觸面微凸體臨界接觸面積ac代入到式(23)中去,可得到主動圓盤-鋼球接觸面微凸體法向接觸剛度公式為: (26) 主動圓盤-鋼球接觸面為曲面接觸,因此還需要引入主動圓盤-鋼球接觸面微凸體分布函數n(a)的修正系數λ,將主動圓盤-鋼球接觸面微凸體分布函數修正為n′(a),其計算式為: (27) 將修正后的主動圓盤-鋼球接觸面微凸體分布函數n′(a)代入到式(26)中,可以得到主動圓盤-鋼球接觸面法向接觸剛度的無量綱形式為: (28) 當主動圓盤-鋼球接觸面處于無潤滑作用的狀態下,接觸面只有固體表面法向接觸剛度,但是在潤滑作用下,接觸面的法向接觸剛度由液體和固體兩部分組成,假設粗糙接觸面之間的空間充滿潤滑液,h為潤滑液的厚度,F為施加的名義接觸壓力,因此潤滑液的法向接觸剛度可以定義為: (29) 假設潤滑液內部沒有切向應力,只有法向應力,體積模量B表示單位體積流體變化量引起的壓力波動: (30) (31) 流體中的波速為: (32) 因此潤滑液的接觸剛度為: (33) 進一步簡化計算,潤滑液的等效厚度為: (34) 假設主動圓盤-鋼球接觸面的微凸體高度分布服從正態分布,則微凸體高度在z(x)=[-3σ,3σ]的概率為99.73%,因此接觸面的初始距離可近似等于3σ,即d0=3σ;Δd為粗糙接觸面的等效彈性變形量;Kn為主動圓盤-鋼球固體接觸面的法向接觸剛度。 聯立式(33)和式(34)可得潤滑液的法向接觸剛度為: (35) 對式(35)無量綱化: (36) 此時,在潤滑作用下主動圓盤-鋼球接觸面的法向總接觸剛度為: (37) 采用潤滑介質的聲學特性如表1所示,研究不同潤滑液對主動圓盤-鋼球接觸面法向接觸剛度的影響。 表1 潤滑液材料的聲學特性 圖7所示為在不同分形維數下圓盤-鋼球接觸面不考慮潤滑和不同潤滑液下的法向接觸剛度隨無量綱法向載荷增加的變化曲線。由圖7可以明顯看出,圓盤-鋼球接觸面法向接觸剛度受潤滑作用影響較大,有潤滑作用時接觸面法向接觸剛度明顯比沒有潤滑介質時增加,潤滑液的法向接觸剛度隨接觸載荷的增加變化并不明顯,并且潤滑液為油的接觸面法向接觸剛度大于潤滑液為水的接觸面法向接觸剛度,說明潤滑液對主動圓盤-鋼球接觸面接觸性能具有很重要的影響。 圖7 不同潤滑劑對主動圓盤-鋼球法向接觸剛度的影響 由于隨著分形維數增加,表面將變得更加光滑,真實接觸面積也逐步增大,法向變形量減少,提高了接觸面的接觸性能。但是法向接觸剛度變化規律受分形維數影響較大,還需進一步探究分形維數變化對法向接觸剛度的影響。 為了進一步探究分形維數對主動圓盤-鋼球法向接觸剛度的影響,由式(37)K*-D的關系,對D取不同的數值(D=1.3~1.8)來分析,公式中其他參數取值:G=10-9,φ=0.02,主動圓盤-鋼球材料的硬度與屈服強度的相關系數K=2,彈性模量E=2.12×1011Pa,泊松比υ=0.3,摩擦系數μ=0.3。在傳動機構轉動一個周期的前提條件下得到圖8所示分形維數對主動圓盤-鋼球接觸面法向接觸剛度的影響規律。當D≥1.5時,接觸面法向接觸剛度隨著法向載荷的增大先減小后保持不變。當D=1.3時,隨著法向載荷增加,法向接觸剛度先增大后減小,并且在p*<0.1增加速度較快。當D=1.4時,隨著法向載荷增加,法向接觸剛度先增大后不變,在p*<0.1增加速度也較快。通過數值計算發現,接觸剛度在不同分形維數影響下呈現不同的變化趨勢,K*與p*之間的關系受分形維數的影響如此之大,可能式(37)中大多數變量都存在D,如al,ac。分形維數D代表了主動圓盤-鋼球半圓軌道微凸體的平整度,增大分形維數,真實接觸面積也隨之增大,法向變形量因此減少,法向接觸剛度增加,接觸面抗變形能力增大,有效地提高了接觸面的接觸性能。因此,通過改善主動圓盤半圓軌道的加工工藝,降低主動圓盤半圓軌道的粗糙度,可以有效提升主動圓盤-鋼球接觸面的接觸性能。 圖8 主動圓盤-鋼球法向接觸剛度與分形維數的關系 由式(37)K*-G的關系,對粗糙度幅值取不同的數值(G=10-10~10-5)進行數值計算,式中其他參數取值:φ=0.02,K=2,E=2.12×1011Pa,υ=0.3,μ=0.3,由于K*在不同分形維數D的影響下,隨著p*的增大呈現不同的變化趨勢,尤其以D≥1.5和D<1.5規律差異表現的尤為顯著。因此,選取D=1.4和D=1.6在傳動機構轉動一個周期的情況下,研究粗糙度幅值G對主動圓盤-鋼球接觸面法向接觸剛度的影響規律,如圖9所示。 圖9 主動圓盤-鋼球法向接觸剛度與粗糙度幅值的關系 當D=1.4時,隨著p*的增大,K*在不同粗糙度幅值的影響下呈現不同的變化趨勢;當G=10-10~10-8時,K*先增大然后保持不變;當G=10-7~10-6時,K*呈現先增大后減小的趨勢; 當G=10-5,K*逐漸減小。同時,當p*保持不變,K*與粗糙度幅值呈遞減關系。當D=1.6時,隨著p*的增大,K*呈現先減小后趨于平穩的趨勢。從整體來看,無論D=1.4還是D=1.6,當p*保持不變時,K*隨著粗糙度幅值的增大而減小。 由圖9可知,K*在不同粗糙度幅值下的變化規律會受到分形維數的影響。降低主動圓盤-鋼球的接觸面的粗糙度幅值,表面將變得更加光滑,真實接觸面積增大,提高了接觸面的接觸性能。 根據式(37)中K*-φ的函數關系,對材料特性參數取不同的幅值(φ=0.02~0.07)進行數值計算。其他參數取值:G=10-9,K=2,E=2.12×1011Pa,υ=0.3,μ=0.3,由于分形維數影響接觸面法向接觸剛度與法向載荷之間的關系,在傳動機構轉動一個周期的前提下,取D=1.4和D=1.6分別研究材料特性參數對K*的影響規律,如圖10所示。 圖10 主動圓盤-鋼球法向接觸剛度與材料特性參數的關系 基于分形理論,建立在潤滑作用下平面正弦鋼球傳動機構中主動圓盤-鋼球接觸面法向接觸剛度模型,并利用數值分析的方法研究關鍵影響因素對接觸面法向接觸剛度的影響規律,得出以下結論: 1)主動圓盤-鋼球接觸面法向接觸剛度受潤滑作用影響較為明顯,有潤滑作用時接觸面法向接觸剛度明顯提升,潤滑液的法向接觸剛度隨接觸載荷的增加變化并不明顯,而與其材料特性和接觸面分形參數有著密切影響關系。 2)分形維數D影響著主動圓盤-鋼球接觸面法向接觸剛度與法向載荷的關系,以D=1.5為界限,其規律前后差異性表現尤為顯著,在其他參數保持不變時,接觸面法向接觸剛度與分形維數呈遞增關系。 3)其他參數保持不變,在一定法向載荷下,接觸面法向接觸剛度與粗糙度幅值G呈遞減關系。因此,可以通過降低半圓軌道表面粗糙度來提升主動圓盤-鋼球接觸面的接觸性能。 4)其他參數保持不變,在一定法向載荷下,接觸面法向接觸剛度與材料特性參數φ呈遞增關系。對于軟材料而言,彈性接觸面積會隨著φ的增加而增大,以此可以提升接觸性能。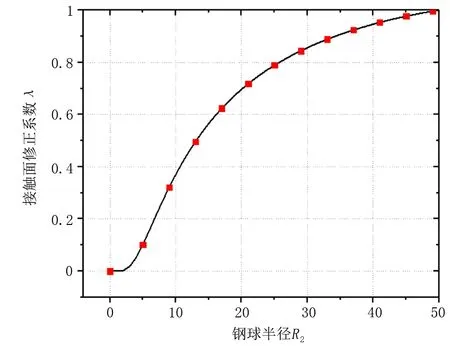
2 法向接觸剛度模型的建立
2.1 單微凸體法向接觸剛度模型
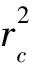
2.2 固體表面接觸法向接觸剛度模型
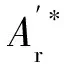
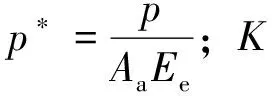
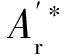
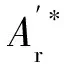
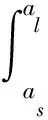
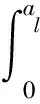
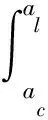
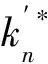
2.3 潤滑液法向接觸剛度
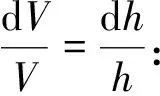
3 仿真結果分析
3.1 潤滑液對法向接觸剛度的影響

3.2 法向接觸剛度與分形維數D的關系
3.3 法向接觸剛度與粗糙度幅值G的關系
3.4 法向接觸剛度與材料特性參數φ的關系
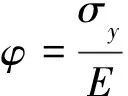
4 結論

