一個高中數學建模問題的探究與思考*

佛山市南海區第一中學(528200) 徐守軍

《普通高中數學課程標準(2017年版2020年修訂)》將數學建模作為高中數學課程的一個組成部分,明確將數學建模列為六大數學學科核心素養之一,并指出:數學建模是對現實問題進行數學抽象,用數學語言表達問題、用數學方法構建模型解決問題的素養.數學建模是高中生數學學習的一種新嘗試,為學生提供了自主學習的空間,有助于學生體驗數學與日常生活的聯系,有助于學會運用數學知識解決生活中的問題,更有助于體會數學在生活和其他學科中的價值.

1 數學建模的內涵

在高中階段,很多學生僅僅把數學當成是為了升學學科,對其在現實世界中的應用不甚了解,其中很多人高考之后便不再關注數學.這對學生未來發展不利.為了破除這樣的觀念,教師需要在高中教學乃至整個基礎教育階段中常常滲透數學建模思想,讓學生從心里認同數學在現實世界的作用.

數學建模過程主要包括以下4個步驟:①在實際情境中從數學的視角發現問題(章建躍對這一步驟表述為“對現實問題進行數學抽象”); ②提出問題、分析問題、建立模型;③確定參數、計算求解; ④檢驗結果、改進模型,最終解決實際問題.學生在實際問題的解決過程中怎么建模是關鍵,下面以一個“停車距離問題”為例來研究數學建模過程.

2 數學建模的過程

2.1 問題的提出

道路安全關系到千家萬戶,隨著經濟的發展,家用小汽車越來越普及,然而車輛在行駛過程中經常會遇到一些突發狀況,如果駕駛員及時采取緊急制動,需要多遠才能停下來呢?另外,在我國道路交通安全條例第80 條中明確規定,高速公路上,車速超過100 公里每小時,應與同車道前車保持100 米以上的車距.規定100 米以上車距的依據是什么呢?

2.2 問題的分析

汽車安全距離一般要大于停車距離,影響停車距離的因素通常包括許多方面,如駕駛員反應時間、汽車行駛速度、天氣狀況、道路情況、汽車輪胎紋路、剎車效果等.總結起來,大致分為兩大類:反應時間(反應距離)、剎車效果(制動距離).汽車緊急制動大概要經歷以下過程,首先是發現危險,做出剎車決定,并踩下剎車.其次是駕駛員踩下剎車,直至汽車完全停止.我們將汽車在反應時間行駛的距離稱為“反應距離”,在制動過程中滑行的距離稱為“制動距離”.

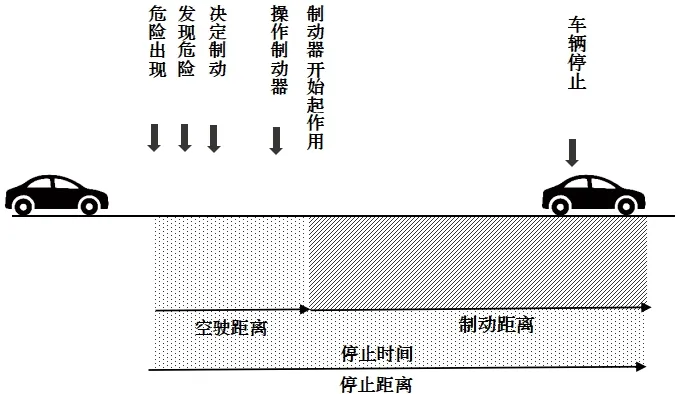
圖1

2.3 模型的建立

由以上分析可知,停車距離包括反應距離和制動距離,設停車距離為d,反應距離為d1,制動距離為d2,得到停車距離為d=d1+d2.

(1)假設反應時間內車輛勻速行駛,速度為v,駕駛員反應時間為t,根據物理知識得到反應距離d1=atv,其中a為(大于0)待定系數.由于t很難確定具體的數值,因此,最終只能確定d1與v成正比,把這個關系表示為d1=av.

(2)假設剎車受力大小近似等于汽車輪胎與路面的摩擦力,制動距離是剎車受力與汽車速度的函數.根據物理知識,例如能量守恒、牛頓第二定律,得d2=,其中a1為加速度,得到制動距離與汽車速度平方成正比,不妨表示為d2=bv2,其中b為待定系數,b=.

綜上,可以建立數學模型d=d1+d2=av+bv2.

2.4 模型的求解

通過問題的分析、模型的建立,把實際問題轉化為數學問題,首先思考:

(1)是不是行駛速度越快,停車距離越大?

(2)是不是反應時間越長,停車距離越大?

接下來,就是運用數學模型來解決問題.模型的系數是由模型的假設和獲取數據的方法確定的,一個好的模型,當采集的數據發生變化時,模型系數也會跟著變化.收集數據方法很多,可通過實驗獲得數據,也可根據網絡獲取數據.注根據表中所給數據,可計算相應參數(a,b)取值.

結合以上數據,通過不同計算方式,都可近似求解模型.

解法一由表1 計算的每一行中相應a和b的值,我們發現a和b的波動都不是很大,它們的平均值分別為a ≈0.209,b ≈0.0058,這組數據可以作為對參數a和b的一種估計.于是,通過試驗數據得到了停車距離模型一:d=0.209v+0.0058v2.

表1 美國公路局公布的試驗數據(來源網絡)

解法二由于在d1=av中d1與v線性相關,由線性回歸分析知數組滿足d1=av.由表1 中的試驗數據計算得=16.8231,=80.3846,因此a=≈0.209.同理,d2與v2線性相關,可求得b=≈0.0062.通過試驗數據得到了停車距離模型二:d=0.209v+0.0062v2.

2.5 模型的評價

對兩種模型進行比較,根據表1 數據,不妨設兩種模型分別d3=0.209v+0.0058v2,d4=0.209v+0.0062v2,則經過誤差計算得表2:

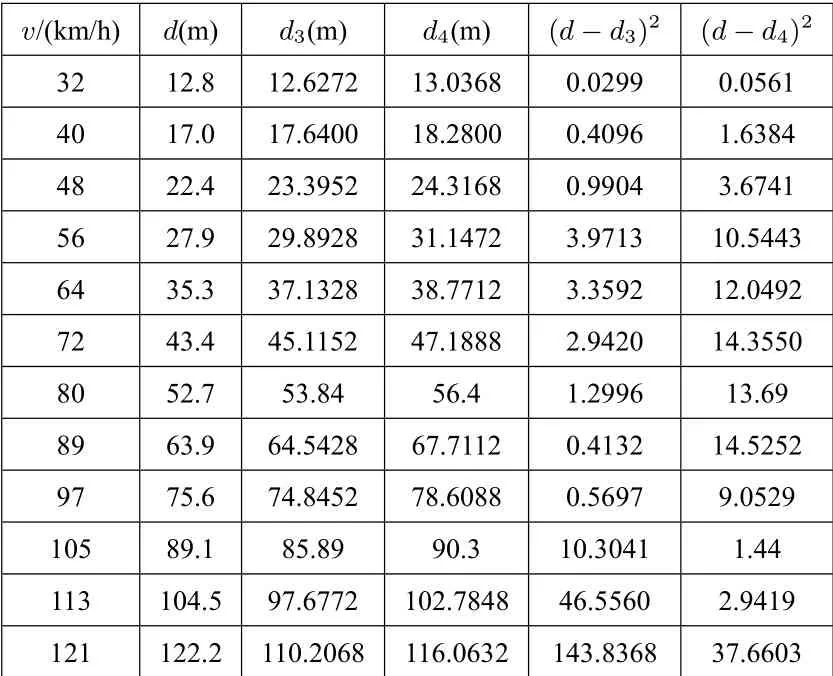
表2 模擬誤差計算

對表2,我們分別求最后兩列值之和得:

D1=0.299+···+143.8368=214.6818,

D2=0.0561+···+37.6603=121.6274.

顯然,D2< D1,所以模型二d=0.209v+0.0062v2誤差和更小,模型效果更好.

說明(1)模型中參數的確定方法有時是不唯一的,科學地選擇參數可以有效地減小模型的誤差; (2)在建立模型過程中,“基本假設”沒有考慮影響停車距離的非關鍵因素,但在實際生活中,由于各種客觀因素影響,有時非關鍵因素也會成為關鍵因素.

2.6 模型的應用

回應課前問題,法規中“100 米以上”的依據是什么?我們發現,當速度達到100 公里每小時時,根據模型計算,停車距離達到82.9m,實際操作過程中,可能存在一定誤差,還可能存在駕駛員違規等現象.法規為了盡可能保證行駛安全,才規定了100 米以上的要求.

3 數學建模的步驟

從現實世界中發現問題,提出問題、分析問題、收集數據、建模模型、求解模型、評價模型,最后又回到現實生活應用模型.如圖2 所示.

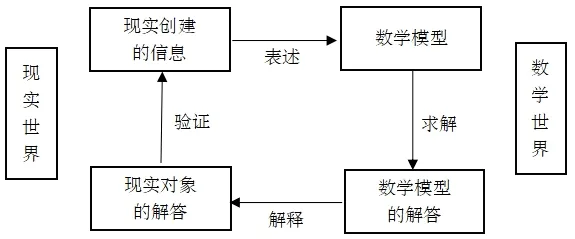
圖2

4 數學建模教學思考

研究停車距離問題的過程就是數學建模的過程,在建模過程中根據實際問題進行數據的收集與處理,從而建立相應的模型、優化模型并應用于實際問題.

4.1 數學建模帶來課堂變革

本節課相比較傳統的“老師講學生聽”的教學模式,數學建模中的合作探究環節使學生更多的參與到課堂中來,課前需做好相應的小組分工,在課堂上有明確的小組合作任務,并給予充分的時間進行小組合作探究,充分的思考和討論提出的問題,提升學生自主學習、自主歸納的能力.

4.2 數學建模要重視數據處理

本節課借助物理背景確定數學模型,教學重點從數學模型的探究,調整到數據處理與數學模型的優化上來,將重點落在系數的求解與模型的優化,這樣的設計更貼合學生學情,讓學生充分進行探究,分享各種方法在實現數學建模過程中的優與劣,符合學生的最近發展區.同時,培養了數學核心素養,從而提升學生的綜合能力.