基于目標分類的數(shù)學解題教學的思考

康杰 黃煒 劉潔

- 編者按 -

“雙減”不只是減輕學生的負擔問題，其深層意蘊是教育本質(zhì)的回歸、教育規(guī)律的彰顯，直接指向校內(nèi)教育尤其是課堂教學質(zhì)量的進一步優(yōu)化改革。“雙減”下如何高質(zhì)量開展課堂教學，回歸育人本質(zhì)，彰顯育人規(guī)律？這是所有教師都會面臨的現(xiàn)實問題。本刊將陸續(xù)呈現(xiàn)各學科優(yōu)秀教研成果，以期為教師高效開展課堂教學助力，為落實“雙減”要求蓄能引航。本期，我們推出的是初中數(shù)學學科教學中“基于目標分類的數(shù)學解題教學”方面的探索。

提高課堂教學質(zhì)量是落實課程標準、發(fā)展教師專業(yè)能力和提升學生學業(yè)水平的需要。為此，《關于深化教育教學改革全面提高義務教育質(zhì)量的意見》指出：強化課堂主陣地作用，切實提高課堂教學質(zhì)量。[1]

縱觀中國初中數(shù)學教育教學的歷史，在課程標準和教學大綱中的作業(yè)往往指課堂練習和課外練習兩種，關于課外作業(yè)的表述不多，但對課堂練習的建議寫得比較詳細。例如，1929年《初級中學算學暫行課程標準》中的“作業(yè)要項”提出了“課室練習”應“每次黑板上的練習以后，應有時間說明算式和解釋的理由”，“課外練習”應“課外單紙上的練習可與同班討論，但要自己懂得‘學習心理’的歷程的重要，不應抄襲別人的演草”。又如，1932年《初級中學算學課程標準》中的 “作業(yè)要項”提出了“教師練習”應注意“初中學生對于算學一科，最感困難，宜在教室，多予練習與復習之機會，務使學生課外作業(yè)時間，得以減少”。再如，1992年《九年義務教育全日制初級中學數(shù)學教學大綱（試用）》中的“正確組織練習”指出“為了使練習能起到應有的作用，應注意以下幾點：（1）目的要明確，題目要精選。（2）題量要適度，首先要保證有足夠的基本題。析題難度要適中，布置作業(yè)要區(qū)別對待。對學習有困難的學生，要給予必要的輔導…”[2]上述材料顯示了初中數(shù)學教育教學中練習和解題的重要，也反映出練習不當是學生學習壓力過大的主要因素。

1.學生數(shù)學作業(yè)負擔過重的原因分析

筆者通過對部分北京市中學生的調(diào)研發(fā)現(xiàn)，學生認為數(shù)學作業(yè)負擔過重的原因不在于數(shù)學作業(yè)多，而在于看似不多的題量，卻需要耗費大量的時間和精力，甚至有學生形象地比喻道：做數(shù)學一道題的時間等于其他有些學科一張卷子的時間。

產(chǎn)生以上問題的原因主要有兩點，一是數(shù)學自身的學科特點決定的。數(shù)學的公理化和形式化要求學習者具有較高的邏輯思維和抽象能力。數(shù)學的原理（公式、定理等）所具有的廣泛應用性和數(shù)學方法具有的靈活性又導致了學生在解決具體問題時遇到障礙，常常覺得可用的方法很多，但真正用得上的很少。二是目前的數(shù)學解題教學中存在的問題造成的。在當下評價背景下，解題是基本形式和主要內(nèi)容，出其不意、攻其不備的命題方式也促使師生陷入題海之中。

在解題教學實踐中，“該選用什么樣的例題”“為什么很多典型問題反復講解后學生依然難以解決”等問題長期困擾著廣大一線數(shù)學教師。涂榮豹教授認為，在數(shù)學解題學習中，學生的主要任務并不是解題，而是學習解題，因此，教師教的重點和學生學的重點，不在于“解”而在于“學解”，以“解”作為出發(fā)點，注重的是解題的結果，以“學解”作為出發(fā)點，注重的則是解題的過程[3]。

2.解題教學的研究簡述

梳理發(fā)現(xiàn)，目前的解題教學研究的方向主要聚焦在兩個部分，即研究解題教學本身與研究解題教學的解題方法與技巧，前者的研究主體主要是教學研究人員，而后者主要是廣大一線教師。

關于解題教學的研究，最重要的代表人物就是美籍匈牙利數(shù)學家波利亞，他專門研究了解題的思維過程，并形成了解題理論。在1944年出版的專著《怎樣解題》（How to solve it）中提出的“怎樣解題表”總結了人類解決數(shù)學問題的一般規(guī)律和程序，對數(shù)學解題研究有著深遠影響[4]。自波利亞的解題理論傳入我國以來，對我國數(shù)學教育亦有著極其重要的指導意義，也給我國中學數(shù)學的教材及教法帶來了很大的轉(zhuǎn)變，徐利治所著的《數(shù)學方法論選講》被認為是波利亞“怎樣解題”研究的延伸與發(fā)展[5]。羅增儒與羅新兵在其《波利亞的怎樣解題表（續(xù)）》中詳細概述了解題系統(tǒng)，分析解題過程，念頭誘發(fā)，問題轉(zhuǎn)換，樸素的元認知觀念與波利亞怎樣解題表的關系，并揭示了波利亞解題思想的目標，即發(fā)現(xiàn)和發(fā)明的方法和規(guī)律[6]。在此基礎上提出有效的解題教學策略，并形成行之有效的教學模式正是我們研究的方向。

3.基于目標分類的數(shù)學解題教學探析

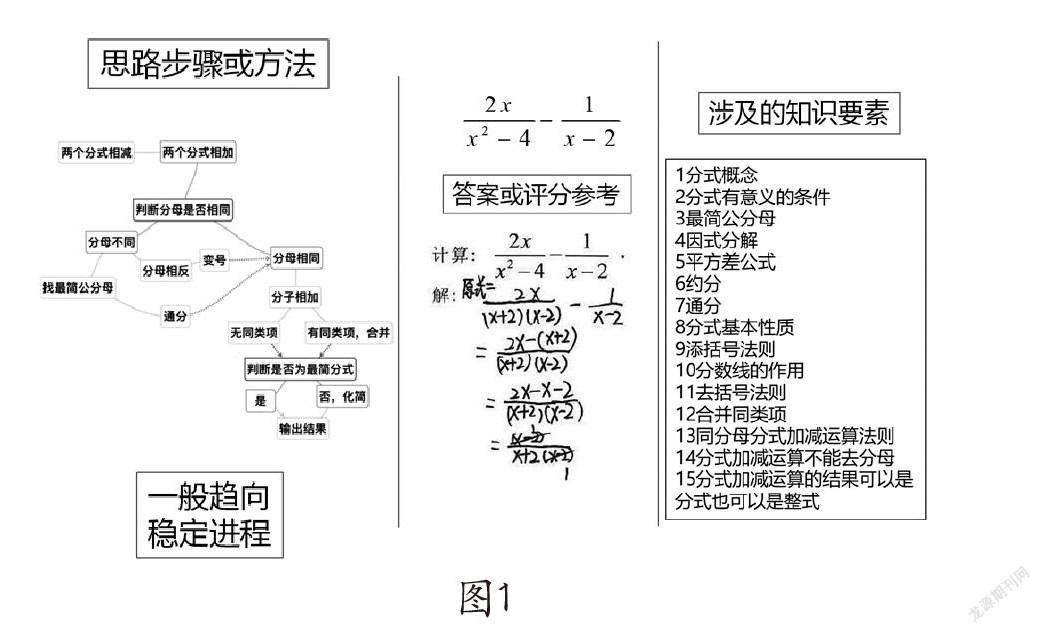
要從根本上提升教師的解題教學水平和能力，進而切實提高課堂教學質(zhì)量，就需要將教師自身置于解題思維活動中，體驗學生的解題過程，分析我們面對題目時的表現(xiàn)。為此，我們借鑒了心理學建立初期常常采用的一種方法——內(nèi)省法，檢查自己解決數(shù)學問題時的想法，進而推斷學生的想法，如圖1所示：

這是一道分式運算的題目，圖1中間一列顯示的是一位學生的解題過程，右邊一列顯示的是在解答這道題目的時候，我們的大腦需要提取的相關概念、法則、公式等多種知識要素，如果有一個或幾個知識要素不能被正確提取，那么解題過程必然會出現(xiàn)各種錯誤。在解答這道題目時，大腦還需要將這些概念、法則、公式有機地聯(lián)系在一起，形成思路、程序或方法，如圖中左邊一列用圖示的方法直觀呈現(xiàn)分式加減法的思維過程。

如果我們從教育目標分類的角度認識如何解答題目，我們會發(fā)現(xiàn)，在解題過程中涉及的知識有概念、法則和公式等，這些知識都屬于事實類知識和概念類知識，而我們的解題思路或者解題方法，則屬于程序類知識，是指某些具體的操作步驟，某種固定的操作順序，運行之后能得到結果。弄清知識的類別，對于我們解釋和分析如何解答一道題、題目能否正確解答及不能正確解答題目的原因，有著重大的意義和作用。從知識分類的角度，還有一類重要的知識——元認知，其中有一種元認知知識稱為認知任務的知識，主要包括：“知道不同的認知任務可能難度不同;知道不同的認知任務可能對認知系統(tǒng)提出不同的要求;知道不同的認知任務可能要求不同的認知策略”[7]。在解題活動中，我們將解題思路、步驟簡稱為“認”，把用到的概念、法則、公式等知識要素簡稱為“知”，將具體題目的解答過程看作一個“任務”，那么這三類知識共同構成了認知任務知識（如圖1）。

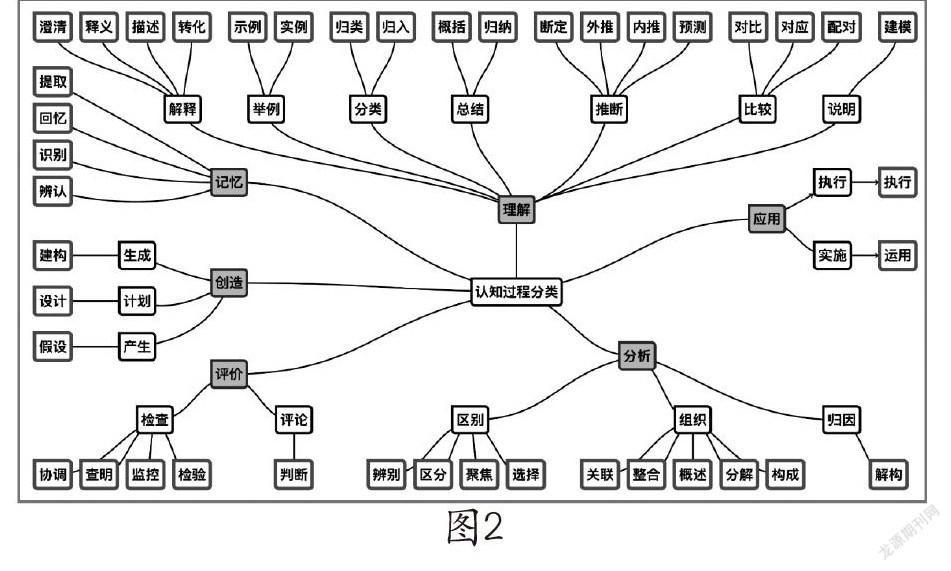
學習認知任務知識需要經(jīng)歷哪些思維活動呢？這就需要我們再從另一個角度分析——認知過程的分類。如圖2，在認知過程的分類中，我們常常把記憶、理解、應用稱作初級認知加工。在做題過程中，需要先提取相關知識，而提取的前提是能夠在理解的基礎上進行記憶，再將提取的知識進行有步驟的應用。如果我們不是應用知識解題，而是對一道題目或任務的解答過程進行研究，分解其中的具體操作步驟，辨別具體操作步驟的依據(jù)，概述解答過程的流程，我們就進行不同于記憶、理解和應用的認知加工，這種認知加工就是分析，也稱為分析能力。

當我們以認知任務知識和分析能力為教學目標時，我們就得到了一種新的課型——析題課，其中的“析”字主要是指分析的意思。在析題課中，最重要的任務不是讓學生做題，而是要給學生題目和解答，讓學生先分析題目解答過程中用到了哪些具體的知識，在這個基礎上，再對解答過程進行概括和總結，用圖示的方法直觀表示解題思路。

教師如何上好一堂數(shù)學解題課，讓學生腦海里的知識得到應用，使得“正者知其原，誤者曉其因”，從而有效減輕不必要的課外作業(yè)負擔，正是本文所研究的課題。

參考文獻：

[1]中共中央 國務院. 關于深化教育教學改革全面提高義務教育質(zhì)量的意見[EB/OL].（2019-06-23）[2022-02-20]http：//www.gov.cn/zhengce/2019-07/08/content_5407361.htm.

[2]課程教材研究所編.20世紀中國中小學課程標準教學大綱匯編（數(shù)學卷）.人民教育出版社，2001年.

[3]涂榮豹.數(shù)學解題的有意義學習[J].數(shù)學教育學報，2001（10）.

[4]G·波利亞著.怎樣解題[M].涂滯，馮承天譯.上海科技教育出版社，2007.

[5]徐利治.數(shù)學方法論選講[M].武漢：華中工學院出版社，1983.

[6]羅增儒，羅新兵.波利亞的怎樣解題表（續(xù)）[J].中學數(shù)學教學參考，2004（05）.

[7]洛林·W.安德森等編著. 布盧姆教育目標分類學（修訂版）[M]. 北京：外語教學與研究出版社，2009.