基于站點線路數的城市公交網絡魯棒性研究

謝怡燃，李國華，楊 波*

(1. 昆明理工大學數據科學研究中心 昆明 650500；2. 昆明理工大學理學院 昆明 650500)

公交系統(tǒng)作為城市的基礎設施，對城市功能的正常運轉有著重要作用。城市公交系統(tǒng)的研究涵蓋多個方面，包括公交網絡的布局優(yōu)化[1-2]、可達性研究[3-4]和公交起訖點分布[5]等。小世界[6]和無標度[7]網絡的提出，推動了各類實證網絡的研究[8-11]，交通網絡作為現(xiàn)實生活中的重要網絡受到廣泛關注。近年來，研究者已經對航空[12-16]、鐵路[10,17]、地鐵[18-19]、公交[20-27]及多種交通工具耦合的多層合作網絡[28]開展了一系列研究。

目前針對公交網絡的研究主要包括拓撲特性、靜態(tài)魯棒性和動態(tài)魯棒性3 個方面。在公交網絡拓撲特性方面，文獻[20]針對波蘭22 座城市的公交網絡的研究發(fā)現(xiàn)，盡管各城市公交網絡規(guī)模不同，但部分拓撲特征擁有普適性規(guī)律。如各城市公交網絡都具有小世界特性，公交站點網絡的度分布服從冪律分布，最短路徑長度服從非對稱單峰型分布等。文獻[21]對北京、上海和南京的公交站點，線路和換乘網絡的研究發(fā)現(xiàn)，公交站點和公交線路網絡的度分布近似服從冪律分布；公交換乘網絡累積度分布近似服從指數分布；公交站點網絡和換乘網絡具有小世界特性。文獻[22]對北京和揚州的公交線路合作網絡的研究發(fā)現(xiàn)，北京和揚州公交線路網絡的度分布分別近似服從指數分布和冪律分布。文獻[23]對北京的加權有向公交站點網絡的研究發(fā)現(xiàn)，網絡中節(jié)點的度和強度分布極不均勻，強度分布近似服從冪律分布，具有小世界和無標度特性。

在日常運營中，道路施工、交通擁堵、自然災害等因素可能導致公交站點在短期內失去功能，進而影響整個公交網絡。網絡的靜態(tài)魯棒性是指，依據某種規(guī)則依次移除網絡中部分節(jié)點或邊后，網絡仍能保持主要功能的能力。在公交網絡靜態(tài)魯棒性方面，文獻[24]采用度值攻擊和隨機故障對北京、上海、南京和杭州的公交網絡進行了研究，發(fā)現(xiàn)公交網絡在隨機故障下的魯棒性強于度值攻擊；度值較大的站點對維持網絡穩(wěn)定性具有重要作用。文獻[25]采用度值攻擊和隨機故障對沈陽市公交站點網絡、換乘網絡、線路網絡、站點?線路雙層網絡、線路?換乘雙層網絡的研究發(fā)現(xiàn)，單層網絡中線路網絡的魯棒性最強；雙層網絡中站點網絡中的節(jié)點失效對線路網絡影響較大；線路網絡中的節(jié)點失效對換乘網絡的影響較大。文獻[26]采用度值攻擊和隨機故障對重慶市公交?地鐵雙層網絡進行的研究表明，雙層網絡的魯棒性強于單層網絡。

網絡的動態(tài)魯棒性是指節(jié)點出現(xiàn)故障引發(fā)級聯(lián)失效時，網絡仍能保持主要功能的能力。在公交網絡動態(tài)魯棒性方面，文獻[27]基于負載?容量級聯(lián)失效模型[29]，采用隨機故障和負載攻擊對北京市公交地鐵關聯(lián)網絡的研究發(fā)現(xiàn)：網絡在負載攻擊下的魯棒性最弱，隨機故障下魯棒性最強；增加地鐵站點容量能更有效地增強關聯(lián)網絡的動態(tài)魯棒性；當站點容量較小時，網絡效率存在非平衡的相變現(xiàn)象。盡管圍繞公交網絡已開展了大量研究，但仍有很多有趣的問題有待進一步探索。

本文首次研究了依據站點線路數(途經某車站的公交線路總數)失效后公交站點網絡的魯棒性。其主要原因是：大部分公交站點被多條公交線路停靠，僅僅考慮節(jié)點度值忽略了這一特性；此外，考慮到同一公交線路對始發(fā)站和終點站加權度的貢獻為1 而對中間車站加權度的貢獻為2，由于城市公交線路數較多，從而導致站點線路數與節(jié)點加權度間存在顯著差異。因此，站點線路數是區(qū)別于度值和加權度值的新參量，研究依據站點線路數失效后公交站點網絡的魯棒性具有實際意義。另一方面，人們對站點重要性的理解也存在差異。度值側重于網絡的連通性，即可到達的相鄰站點越多節(jié)點越重要，而站點線路數則更多關注在某車站是否有大量的換乘可能，即停靠車次是否較多。

1 網絡拓撲結構分析

1.1 網絡模型的構建

公交網絡主要有站點網絡、換乘網絡和線路網絡3 種類型。表1 顯示了不同類型公交網絡的節(jié)點和連邊的定義。本文以公交站點網絡為研究對象，從8684 公交查詢網(https://www.8684.cn/)分別獲取成都、重慶、昆明、貴陽和拉薩5 個城市的公交線路數據(截止2021 年7 月23 日)，建立公交站點網絡模型。

表1 不同類型公交網絡的定義

表2 顯示了網絡的基本拓撲特性。其中，N表示公交站點數，M表示公交線路數，D表示網絡直徑，r表示網絡同配系數， 〈k〉表 示平均度， 〈L〉表示平均路徑長度， 〈C〉表示平均聚類系數。顯然，公交站點網絡具有同配性；相比而言，貴陽公交站點網絡的平均度和聚類系數偏大，網絡直徑偏小，說明該網絡的連接相對緊湊；拉薩公交站點網絡的平均度和同配系數較小，平均路徑長度僅次于成都，說明該網絡的連接相對松散；此外，成都公交站點網絡的平均聚類系數偏小，平均路徑長度和網絡直徑較大，顯示網絡規(guī)模大，連接范圍廣。

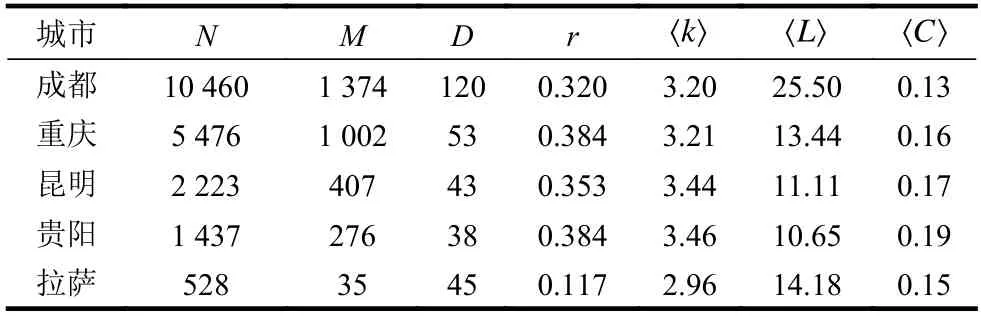
表2 公交站點網絡的基本拓撲特性

1.2 累積度分布

度值選擇性失效下，網絡魯棒性的研究是通過逐步移除度值較大的節(jié)點后，觀察網絡連通性的變化實現(xiàn)的。為描述該移除過程中網絡累積度值的變化，定義網絡的累積度分布為：

圖1 顯示了5 個城市公交站點網絡的累積度分布的半對數擬合曲線。結果顯示：累積度分布近似服從指數分布，即P(k)～e?βk，擬合曲線的指數見表3。累積度分布為指數意味著，在網絡形成過程中，新增站點與已有站點之間的連接可近似視為隨機連接[30]。曲線的斜率描述了在逐步移除較大度值節(jié)點的過程中，度分布變化快慢的趨勢。斜率越大，變化越劇烈，對網絡的影響也越大。從圖1中可以看出，拉薩的累積度分布指數最大，貴陽的最小。

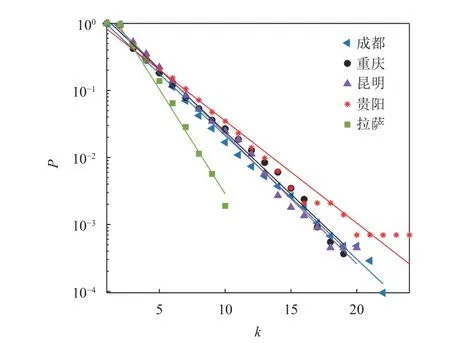
圖1 半對數坐標下公交站點網絡的累積度分布

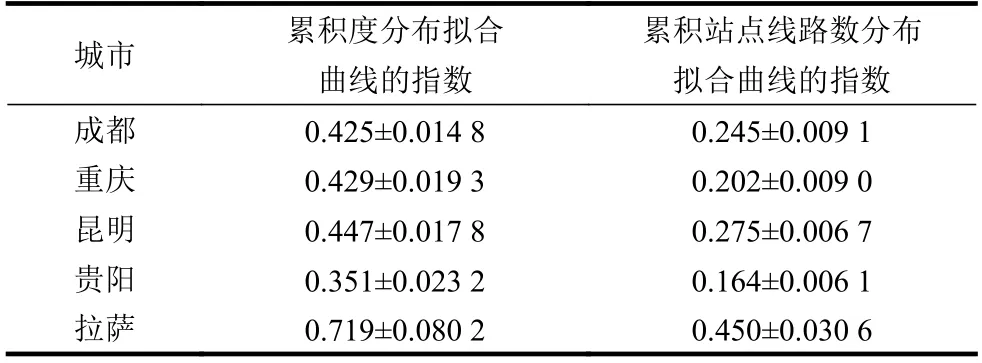
表3 累積度分布和累積站點線路數分布擬合曲線的指數

1.3 累積站點線路數分布

站點線路數是指途經某車站的公交線路總數。本文考慮該值的動機源于，公交站點網絡僅描述了站點間的連接關系而沒有考慮站點被多條公交線路重復經過的情況，且該過程不能通過加權公交站點網絡描述(主要原因是城市公交網絡線路數較多，始發(fā)站和終點站對加權網絡的貢獻與中間車站不同)，因此本文首先對途經站點i的公交線路數量ni進行了統(tǒng)計。然后類比累積度分布定義累積站點線路數分布：

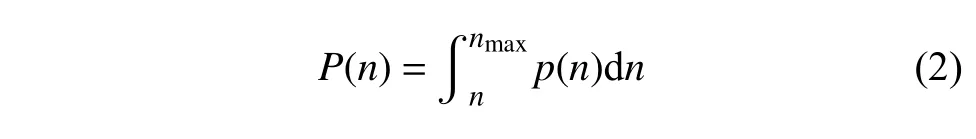
圖2 顯示了5 個城市公交站點網絡的累積站點線路數分布的半對數曲線。顯然，各城市累積站點線路數分布近似服從指數分布P(n)～e?βn，與累積度分布相比，曲線的斜率存在明顯差異，累積站點線路數分布擬合曲線的指數見表3。拉薩的指數較大，昆明和成都次之，其次是重慶，最后是貴陽。

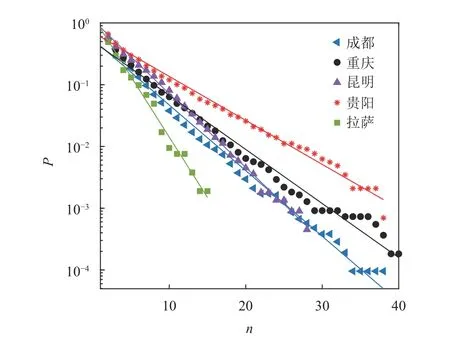
圖2 半對數坐標下累積站點線路數分布

1.4 最短路徑長度分布

在公交站點網絡中，最短路徑長度是指從任意初始站點i出發(fā)，到達任意目的站點j所經過的最少邊數，記為dij。網絡的平均路徑長度定義為網絡中任意兩節(jié)點間最短距離的平均值，表達式為：

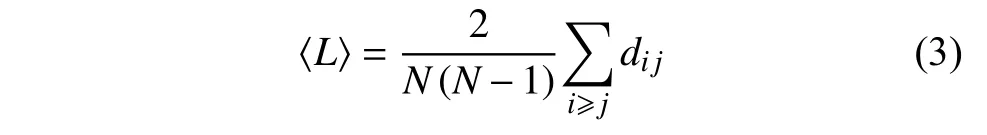
式中，N為網絡的節(jié)點總數。圖3 顯示了5 個城市公交站點網絡最短路徑長度的分布曲線。顯然，重慶、昆明、貴陽和拉薩的最短路徑具有高斯分布特性，而成都的最短路徑長度分布具有長尾特性，出現(xiàn)該特性的原因是成都的公交站點網絡包含了很多郊區(qū)線路，導致部分站點間的最短路徑長度值較大。此外，拉薩的最短路徑長度也較大，在距離值為30 的附近表現(xiàn)出一個下降較為緩慢的平臺期。

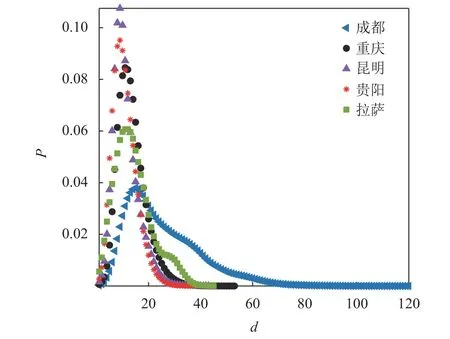
圖3 公交站點網絡的最短路徑長度分布

1.5 介數分布

公交站點網絡中站點i的介數是指經過該站點的最短路徑數所占的比例，記為BCi。定義如下：

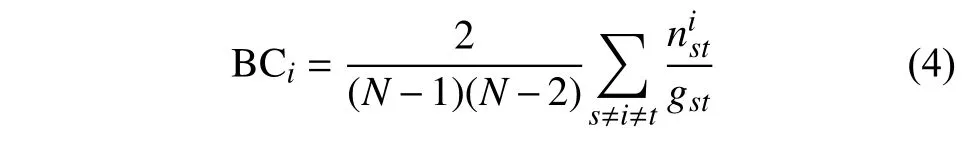
式中，gst代表從節(jié)點s到節(jié)點t的最短路徑數目；代表從節(jié)點s到節(jié)點t的最短路徑中經過節(jié)點i的數量。由式(4)可知，歸一化介數值的取值較為分散，無法直接得到介數的分布情況。為進一步研究介數選擇性失效下網絡中累積介數的變化，定義累積介數分布為：

累積介數分布如圖4 所示，可以看到，相同介數值時，拉薩的累計值較大；昆明、貴陽次之；成都、重慶較小。在公交站點網絡中，介數較大意味著該站點被很多線路的最短路徑途經，所以，累積介數值大小顯示了一個城市對部分站點的依賴程度。

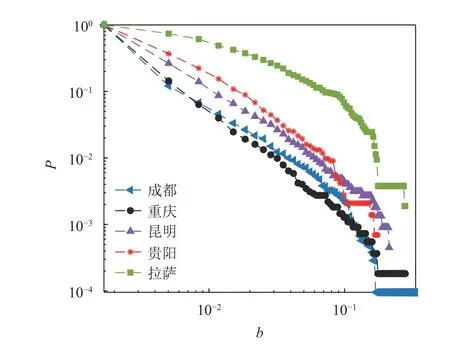
圖4 公交站點網絡的累積介數分布

2 網絡靜態(tài)魯棒性分析

2.1 失效方式與評價指標

網絡靜態(tài)魯棒性分析是依據某種規(guī)則依次移除網絡中部分節(jié)點或邊后，研究網絡連通性和網絡效率發(fā)生的變化。考慮到現(xiàn)實生活中，交通擁堵、道路維修和自然災害等事故會造成公交站點短期內失去功能，因此本文研究不同的站點失效方式下，公交站點的網絡魯棒性。具體可分為節(jié)點的隨機失效和選擇性失效[31]，隨機失效(RA)模擬自然災害對公交網絡的影響，選擇性失效模擬公交樞紐站點堵塞和維修對公交網絡的影響。由于任意節(jié)點的失效都伴隨網絡拓撲結構的變化從而引發(fā)失效指標值的改變，可將選擇性失效細分為靜態(tài)選擇性失效和動態(tài)選擇性失效。靜態(tài)選擇性失效是指在初始網絡中計算各節(jié)點的選擇性失效的指標值，按降序依次移除節(jié)點，包括靜態(tài)度值選擇性失效(DA)、靜態(tài)介數值選擇性失效(BA)和站點線路數選擇性失效(NBLS)。動態(tài)選擇性失效是指依據當前網絡的選擇性失效指標值移除節(jié)點后，重新計算新網絡的指標值作為下一輪移除節(jié)點的依據，包括動態(tài)度值選擇性失效(UDA)和動態(tài)介數值選擇性失效(UBA)。

當某個節(jié)點失效時，移除該節(jié)點將引發(fā)網絡連通性的改變。為描述這一變化，研究者選取網絡最大連通子圖的相對大小S作為網絡魯棒性的評價指標，表達式如下：

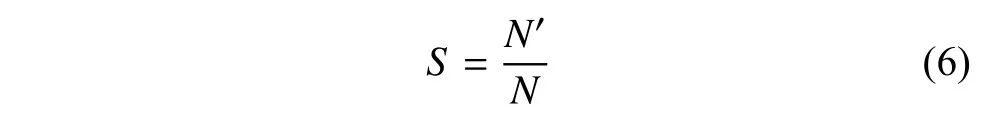
式中，N表示初始網絡中的節(jié)點總數；N'表示移除節(jié)點后網絡中最大連通子圖的節(jié)點總數。

網絡的魯棒性可以通過網絡完全崩潰時(S=0)移除節(jié)點比例的臨界值來衡量。然而，當多個網絡的最大連通子圖相對大小的變化曲線交錯或臨界值相近時，僅通過觀察很難分辨優(yōu)劣。本文引入描述全局魯棒性的評價指標R，表達式為[32]：

式中，Q表示失效的節(jié)點數量；S(Q)表示移除Q個節(jié)點后最大連通子圖的相對大小。

本文設置每次移除0.01N數量的公交站點，在選擇性失效下，當多個站點的失效指標值相同時，隨機移除其中之一。為獲得穩(wěn)定的計算結果，需要對計算結果進行平均，選擇性失效取10 次平均后的結果，隨機失效取5 000 次平均后的結果。

2.2 結果分析

在公交站點網絡中，站點失效將引發(fā)網絡連通性的改變。圖5 依次顯示了站點線路數選擇性失效、隨機失效、度值、動態(tài)度值、介數值和動態(tài)介數值選擇性失效下，不同城市的最大連通子圖相對大小S隨移除節(jié)點比例f的變化關系。顯然，相同的失效方式下，不同城市表現(xiàn)出不同的變化趨勢。

圖5a 和圖5c 展現(xiàn)出不一樣的變化規(guī)律，說明站點線路數并非重復的平庸參數。圖5c 與圖1 存在對應關系，即累積度分布曲線斜率越大，度值選擇性失效下最大連通片占比變化越快，網絡的魯棒性越差。產生該現(xiàn)象是因為度值是網絡結構的直觀描述，度值選擇性失效直接反映了網絡連通性的變化。相應的圖5a 和圖2 的對應關系相對弱一些，除貴陽的魯棒性表現(xiàn)較為突出外，其他城市隨著移除節(jié)點比例的增加網絡魯棒性變化各異。圖5e 和圖4 的對應關系更差，很難從累積介數分布曲線推演網絡的魯棒性。綜上，度值、站點線路數和介數值選擇性失效對最大連通片占比的影響存在差異，本文認為這主要與站點失效方式對網絡刻畫角度的不同有關，度值是公交站點網絡的直觀描述，站點線路數是網絡中公交線路運行狀態(tài)的描述，而介數以被最短路徑通過為標準。圖5b 描述了隨機失效下，不同城市最大連通片占比隨移除節(jié)點比例的變化關系。當移除少部分站點時，成都的最大連通子圖相對大小S下降較快，而隨著移除站點數的增加，拉薩快于成都。該現(xiàn)象可能是由公交站點網絡的拓撲結構差異引起的，成都公交網絡相對松散，包含很多郊區(qū)線路，隨機移除節(jié)點對郊區(qū)線路的影響較大。拉薩由于城市規(guī)模的限制，對城市中心節(jié)點的依賴較為明顯。此外，隨機失效下，S隨著移除節(jié)點比例f的變化趨勢較為平緩，幾乎不存在突然跳變現(xiàn)象。這表明選擇性失效對公交站點網絡的破壞性強于隨機失效。

圖5d 和圖5f 為動態(tài)度值選擇性失效和動態(tài)介數值選擇性失效下，不同城市的最大連通片占比隨移除節(jié)點比例的變化關系。可以看到不同城市的變化曲線幾乎坍縮在一起，這說明不斷修正選擇性失效指標可以部分消除不同網絡結構對魯棒性的影響。

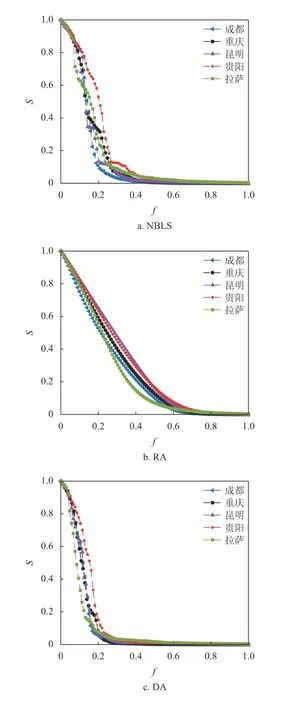
圖5 公交站點網絡最大連通子圖的相對大小S 與移除節(jié)點比例f 的關系

為進一步比較不同節(jié)點失效方式對同一網絡結構的影響，圖6 和表4 分別顯示了5 個城市在不同失效方式下的最大連通子圖相對大小S隨移除節(jié)點比例f的變化關系和R值的大小。顯然，不同網絡結構在隨機失效下R值最高，S隨著移除節(jié)點比例f的變化趨勢最平緩，魯棒性最好。動態(tài)選擇性失效(UDA 和UBA)下，R值較低，網絡魯棒性較差。靜態(tài)選擇性失效的魯棒性因網絡結構的不同而異。總之，表4 中的數據與圖片中曲線的變化趨勢相符，隨機失效對網絡的破壞弱于選擇性失效；選擇性失效下，動態(tài)選擇性失效對網絡破壞強于靜態(tài)選擇性失效。

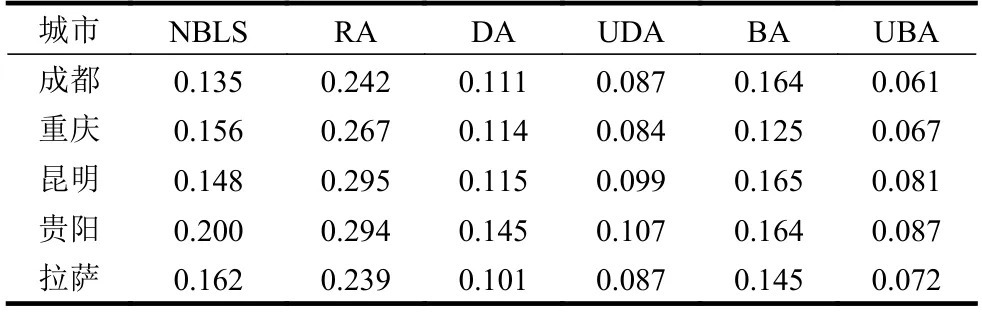
表4 公交站點網絡在不同失效方式下的R 值

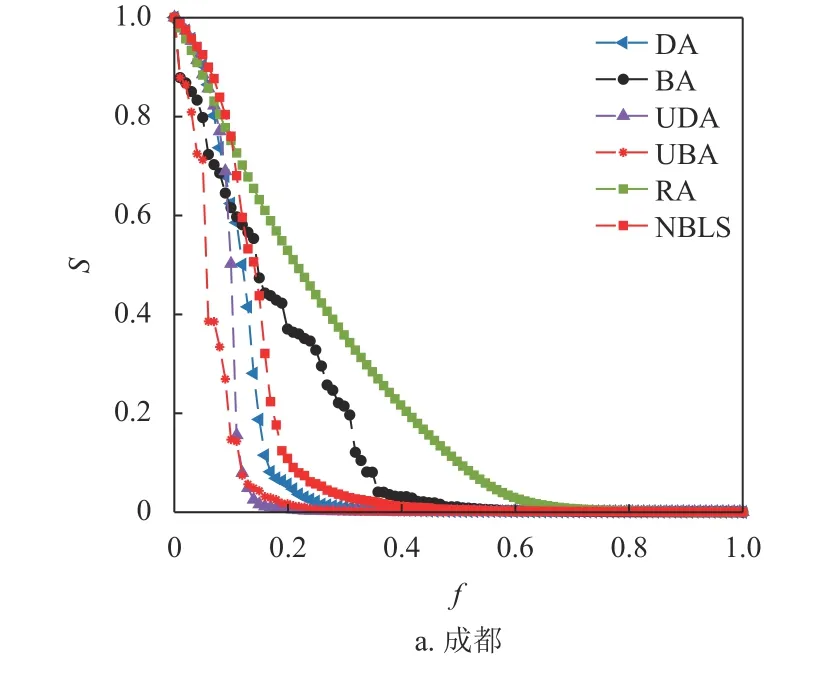
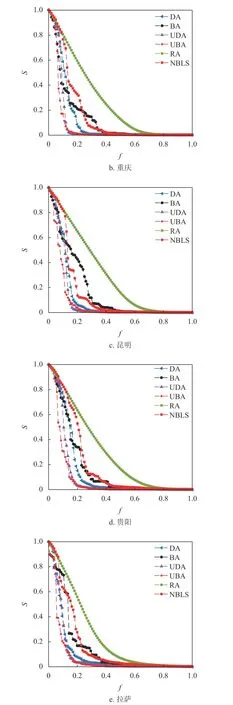
圖6 各城市公交站點網絡最大連通子圖的相對大小S 與移除節(jié)點比例f 的關系

3 網絡動態(tài)魯棒性分析

在分析網絡靜態(tài)魯棒性時，假設各站點發(fā)生故障是相互獨立的。但在現(xiàn)實生活中，網絡各節(jié)點相互關聯(lián)，一個節(jié)點的故障可能會導致相鄰節(jié)點的故障，甚至引發(fā)網絡中部分節(jié)點無法正常工作，這一現(xiàn)象稱為級聯(lián)失效。網絡動態(tài)魯棒性是指，節(jié)點出現(xiàn)故障引發(fā)級聯(lián)失效時，網絡仍能保持正常功能的能力。

3.1 負載?容量級聯(lián)失效模型

假設網絡中每個站點都擁有負載量和容量兩個值，容量是站點所能承載的最大負載量，當負載量小于等于容量時，站點正常工作；當負載量超過容量時站點失效。考慮到站點負載分布與網絡度分布高度相關[29,33]，假設公交站點i的初始負載量Li由下式確定[34]：

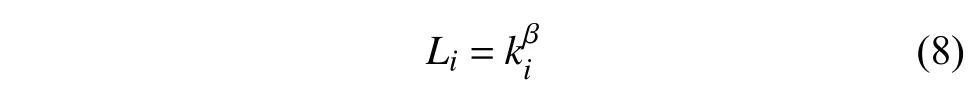
式中，β 是節(jié)點負載控制參數。

站點容量Ci是站點i可承載的最大負載量，根據負載?容量級聯(lián)失效模型[29]，假設站點容量與負載由下式確定：

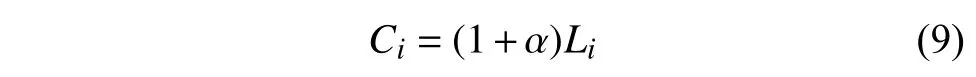
式中，α 表示節(jié)點負載容忍參數。

當某個站點i失效時，該站點的負載Li會依據鄰居站點容量進行重新分配。i的鄰居站點j獲得的分配負載?Li→j為[34]：

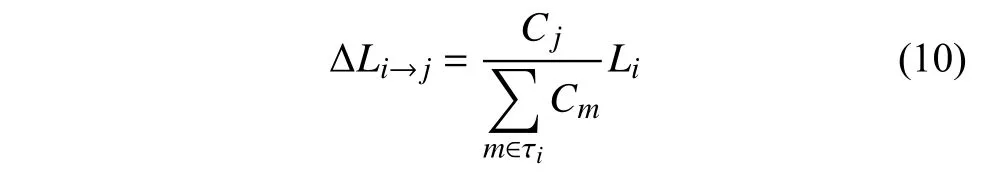
式中，τi表示i的鄰居集合。站點j的當前負載量包括初始負載和分配負載。若當前負載超過容量將引發(fā)站點j失效，失效站點將繼續(xù)分配負載給鄰居站點。

3.2 算法描述

負載?容量級聯(lián)失效算法如下：

1) 初始化公交站點網絡，輸入參數α、β 的值，設置失效站點數a為0，依據式(8)和式(9)分別計算各節(jié)點的初始負載量和容量，依據式(6)計算當前網絡最大連通子圖的相對大小S。

2) 選擇節(jié)點的失效方式，移除失效節(jié)點，失效站點數a的值加1。計算當前網絡中各節(jié)點的負載量，判斷是否產生過載站點，若產生則執(zhí)行步驟3)和4)；若不產生則執(zhí)行步驟5)。

3) 過載站點依據式(10)將負載分配給鄰居站點，然后移除該站點。

4) 重新計算當前網絡各節(jié)點的負載量，判斷是否產生過載節(jié)點，若產生則回到步驟3)；若沒有則執(zhí)行步驟5)。

5) 計算當前網絡最大連通子圖的相對大小S，判斷S是否為0，若S≠0 則回到步驟2)；若S=0 則算法結束。

運用選擇性失效和隨機失效兩種方式分別對5 個城市公交站點網絡的動態(tài)魯棒性進行研究。選擇性失效包括：NBLS、DA、BA、UDA 和UBA。選擇性失效時，若存在多個站點失效指標值相同的情況，則隨機移除其中一個站點。為確保最終結果的準確性，需要對計算結果進行平均，BA 和UBA 取10 次平均后的結果，其余選擇性失效取100 次平均后的結果，隨機失效取5 000 次平均后的結果。

3.3 結果分析

圖7 顯示了在α=1，β=1.5 時，不同失效方式下，不同城市公交站點網絡最大連通子圖的相對大小S隨失效站點數a的變化關系。隨著失效站點數a的增加，網絡的連通性逐漸降低，最大連通子圖的相對大小逐漸減小。選擇性失效存在連通性的突然躍變，只需移除少部分節(jié)點就能觸發(fā)級聯(lián)失效，由于網絡結構的差異導致躍變點存在差異。隨機失效下，網絡連通性的變化則相對平緩且能夠承受的失效站點數較多，如圖7b 所示。對比圖7c 和圖7d 發(fā)現(xiàn)，度值失效對網絡的破壞性強于更新度值，該結果與靜態(tài)魯棒性相反，其原因可能是，網絡的初始負載和容量由最初的網絡結構確定，部分站點失效后，網絡中最大度節(jié)點不一定擁有最大的負載和容量值。考慮到不同城市可能具有不同的α 和β 值，此處不再對不同城市公交站點網絡的魯棒性進行對比分析。

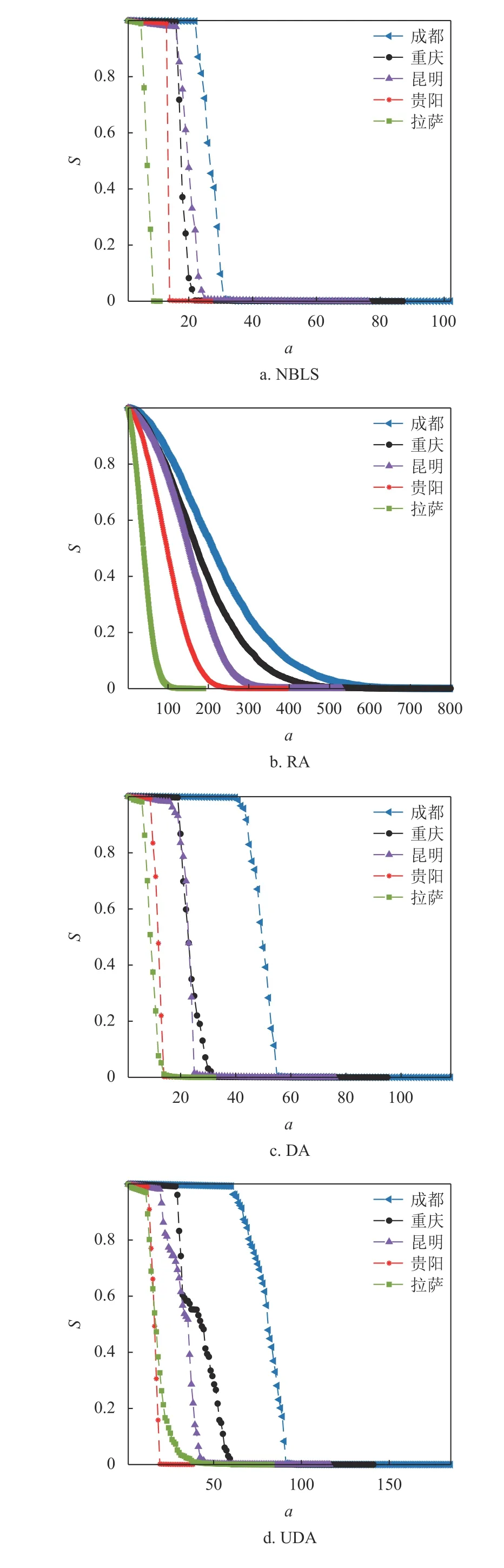
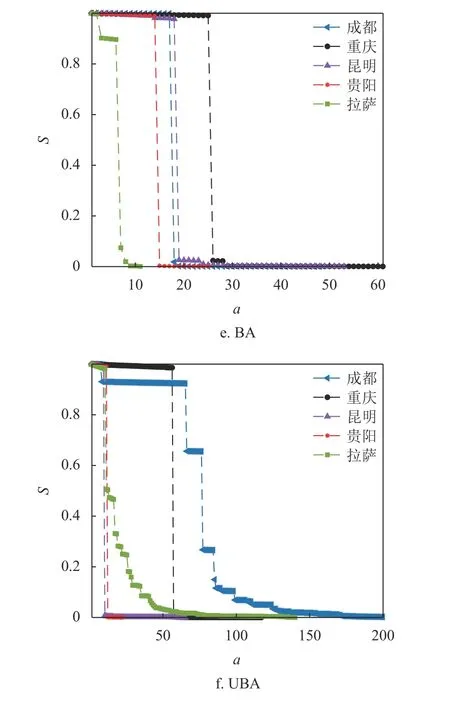
圖7 公交站點網絡最大連通子圖的相對大小S 與失效站點數a 的關系

為進一步研究不同失效方式對同一網絡結構的影響，圖8 分別顯示了5 個城市的公交站點網絡在不同失效方式下，最大連通子圖的相對大小S隨失效站點數a的變化關系。可以看出，隨機失效下的魯棒性遠遠強于選擇性失效，動態(tài)選擇性失效強于靜態(tài)選擇性失效的結論已經不再適用。

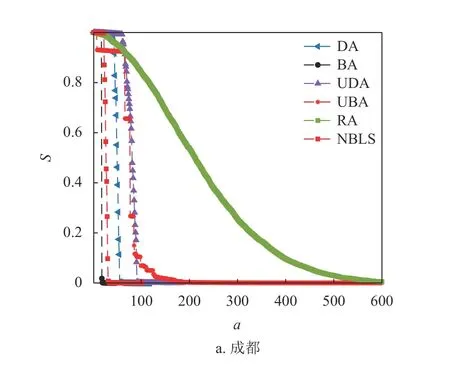
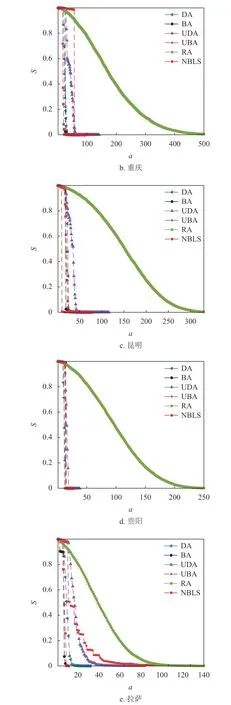
圖8 各城市公交站點網絡最大連通子圖的相對大小S 與失效站點數a 的關系

為探究負載容忍參數α 與負載控制參數β 對網絡動態(tài)魯棒性的影響，本文進一步針對UDA 策略下，網絡最大連通子圖的相對大小首次達到0.01時所需的失效站點數進行了研究。圖9 為α 和β 參數空間內失效站點數相對大小的熱力圖。當β 值相同時，失效站點數a隨著α 的增加而增加。這是因為α 變大導致網絡中各站點的容量增加，提高了網絡的動態(tài)魯棒性。當α 值相同時，失效站點數a隨著參數β 的增加而減少。這是因為β 變大導致網絡中負載的異質性增強，站點間負載量差距變大。少量負載較大的站點失效可能導致整個網絡的崩潰，網絡的動態(tài)魯棒性變差。

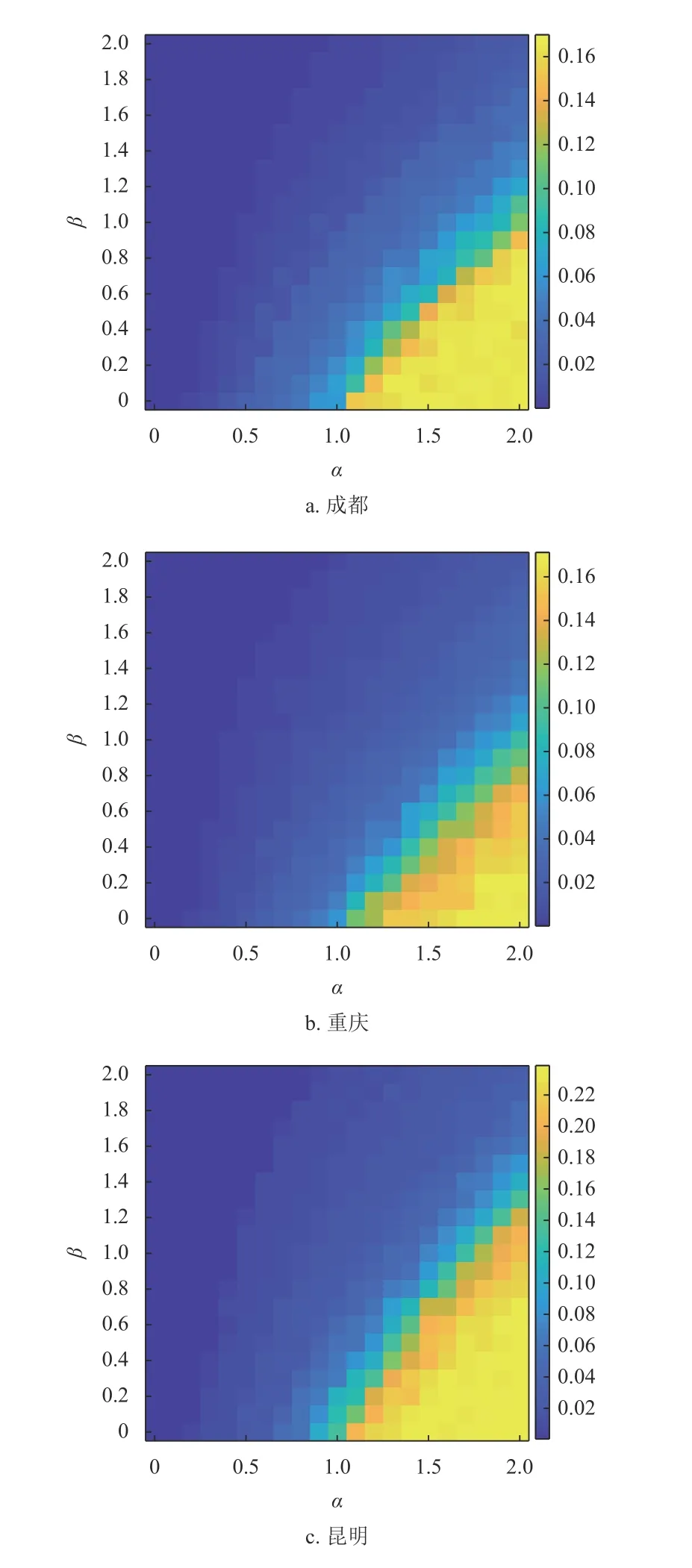
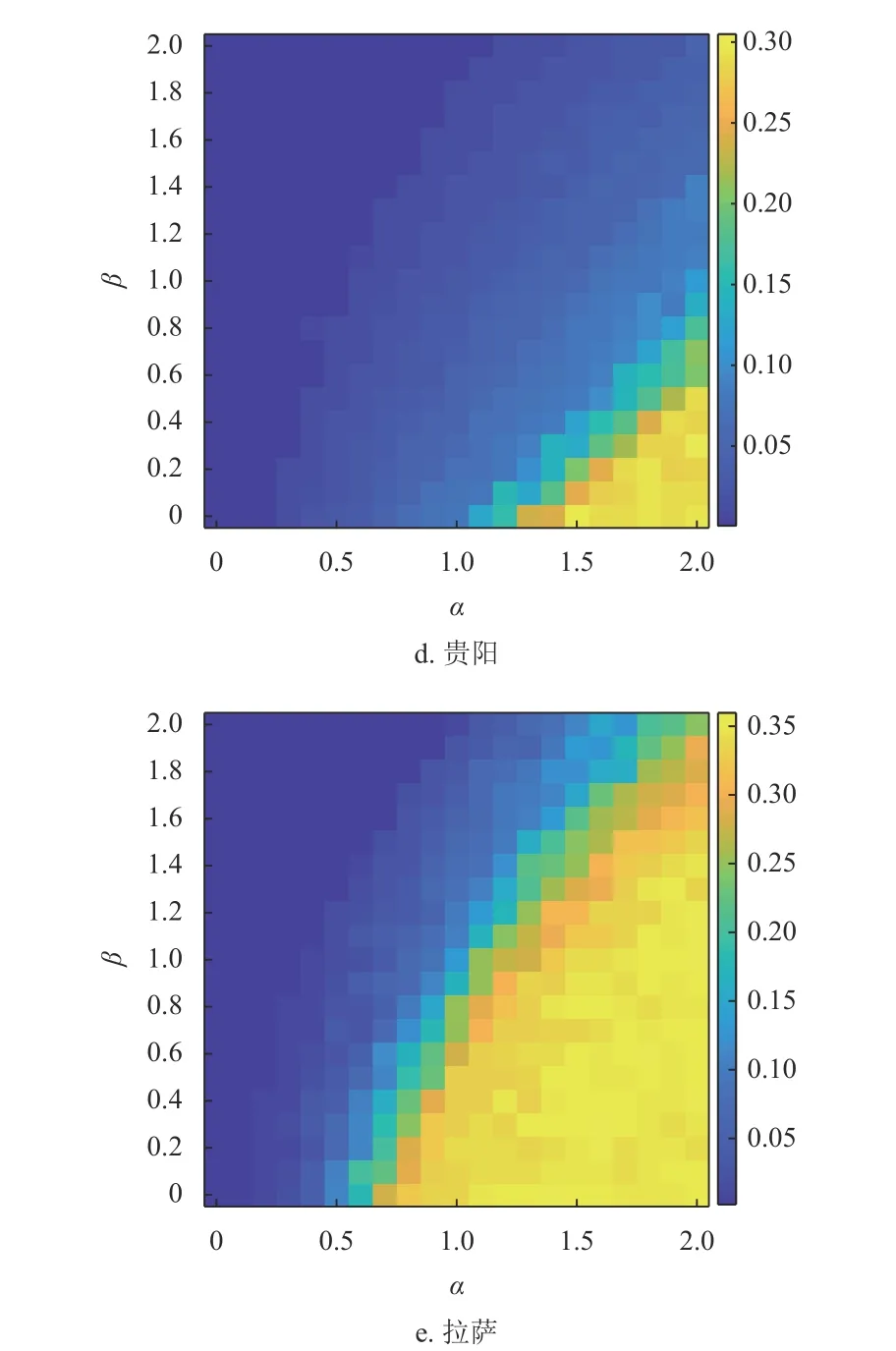
圖9 公交站點網絡最大連通子圖的相對大小S 首次達到0.01 時需要失效的節(jié)點比例

4 結 束 語

本文基于站點線路數(途經某車站的公交線路總數)研究了成都、重慶、昆明、貴陽和拉薩公交站點網絡的拓撲特性、靜態(tài)魯棒性和動態(tài)魯棒性。將站點線路數選擇性失效與廣泛研究的隨機失效、度值、介數值、動態(tài)度值和動態(tài)介數值選擇性失效進行了比較。結果表明：各城市公交站點網絡的累積站點線路數分布和累積度分布近似服從指數分布，指數的取值不同；重慶、昆明、貴陽和拉薩的最短路徑長度分布具有高斯分布特性，成都的最短路徑長度分布具有長尾特性；網絡的靜態(tài)魯棒性與網絡的拓撲結構密切相關，累積度分布曲線斜率越大，度值選擇性失效下最大連通片占比變化越快，網絡的魯棒性越差，站點線路數和介數值對最大連通片占比的影響較度值弱一些；對于靜態(tài)魯棒性而言，動態(tài)選擇性失效對網絡的破壞性強于靜態(tài)選擇性失效，但該結論不適用于動態(tài)魯棒性；不論是靜態(tài)魯棒性還是動態(tài)魯棒性，隨機失效下的魯棒性都強于選擇性失效下的魯棒性；增加負載容忍參數α或減少負載控制參數β 可提高網絡的動態(tài)魯棒性。